多源耦合剃齿齿形中凹误差的预测模型

蔡安江，王瑞远

（西安建筑科技大学 机电工程学院，西安 710055）

剃齿齿形中凹误差是齿轮传动产生振动、噪声和降低齿轮使用寿命的主要因素之一，研究剃齿齿形中凹误差对制造高精度齿轮满足科技发展要求有着重要意义。

目前，国内外剃齿齿形中凹误差的研究主要集中在剃齿啮合点载荷、诱导法曲率、相对滑移速度、弹塑性变形量、剃削力和安装误差等单因素对剃齿齿形中凹误差的影响及其形成机理。Zhang等[1-2]对交错轴螺旋齿轮的啮合情况和载荷分布进行研究，认为载荷分布不均是引起齿形中凹误差的重要原因；Hsu等[3-4]通过分析剃齿加工的接触状态来研究径向剃齿对齿面误差的影响。蔡安江等[5-7]基于齿面承载接触分析技术（LTCA）技术分别从齿面载荷、接触变形与剃削力等因素分析了齿形中凹误差的形成机理，认为啮合点的塑形变形是齿形中凹误差出现的主要原因。姚文席等[8]分别从齿面的相对滑移速度和诱导法曲率两个因素分析了齿形中凹误差的形成机理，认为节圆处剃削量过多是齿形中凹误差的形成原因。文献[9-10]在考虑剃齿安装误差的情况下研究了各参数对齿面误差的影响，并提出齿轮安装误差的改进方法；吴震宇等[11]分析了安装误差下刀具和工件之间的相对运动关系来研究安装误差对齿廓形状误差的影响；文献[12-13]通过对包含安装误差的齿面方程与理论齿面方程对比分析，得到了机床各调整参数误差与全齿形法向偏差的变化规律。实际上单因素研究很难去揭示剃齿齿形中凹误差的形成机理，更难以从理论上对剃齿过程产生齿形中凹误差的规律进行定量研究，因此多因素耦合分析对剃齿齿形中凹误差的研究与预测具有重要意义。

本文基于齿轮啮合原理建立了含剃齿安装误差的剃齿分析模型，引入单次切削面积，建立了包含重合度、机床运动参数和安装误差的剃齿齿形中凹误差多源耦合预测模型；通过分析剃齿齿形中凹误差与啮合点单次切削面积的关系来研究剃齿齿形中凹误差的形成机理。

1 建立剃齿分析模型

剃齿加工中，剃齿刀和工件齿轮的轴交角误差ΔΣ 、中心距误差Δa和 两个高速轴的同步误差Δω1和 Δω2都会反应到工件的齿向误差上[12]，因此针对这4个误差参数建立剃齿啮合点几何模型如图1所示。

图1 含安装误差的剃齿啮合几何模型

考虑几何模型中的安装误差参数，根据剃齿刀与工件齿轮的运动关系推导出啮合点的相对滑动速度V为

其中

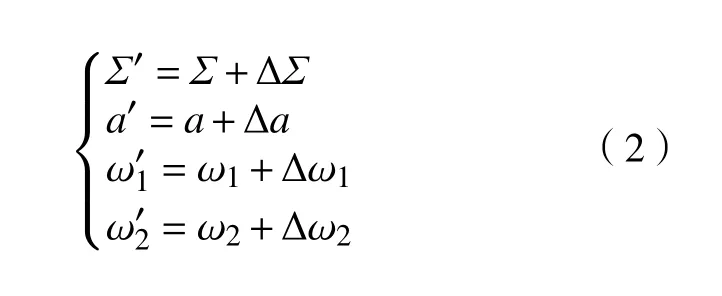
式中：(x,y,z)为 啮合点在坐标系S中的坐标；Σ为剃齿刀与工件齿轮的轴交角；a为中心距；ω1为剃齿刀的角速度；ω2为 工件齿轮的角速度；v02为工件齿轮的轴向进给速度。

根据空间几何关系相对滑移速度V在刀刃垂直方向上的分量切削速度V1为

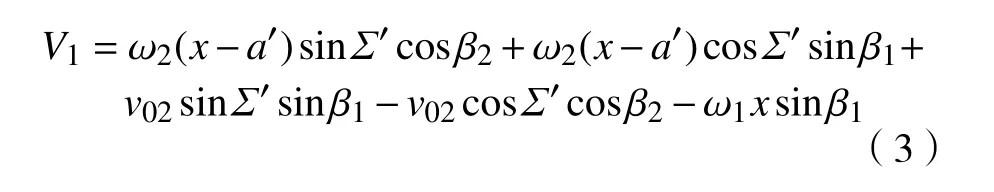
式中： β1、β2分别为剃齿刀与工件齿轮的螺旋角。

安装误差会使啮合点位置发生变化，根据齿轮啮合原理可以求出改变后的啮合点轨迹方程为[13]

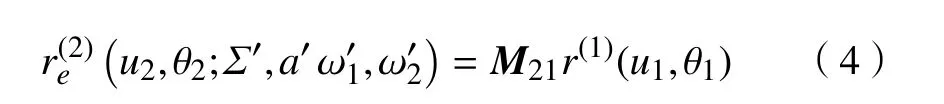
式中：r(1)为剃齿刀在坐标系S1中 的齿面方程；M21为坐标系S1到 坐标系S2的 转换矩阵； (u,θ)为齿面的曲线参变数。啮合点处沿刀齿方向的诱导法曲率K为[14]

根据位置改变后的齿轮啮合轨迹方程可以确定

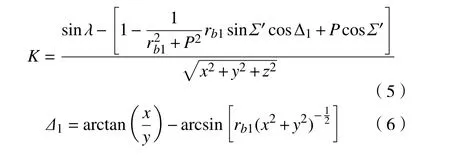
式中：rb1为 剃齿刀基圆半径；λ为齿廓的转角参变数；P为剃齿刀齿面的螺旋参数。

背吃刀量由径向进给量、啮合点压下量和轮齿的弯曲程度决定，剃齿时啮合点的背吃刀量ap为

式中：Δfr为剃齿刀每次径向进给量，当工件齿轮总切削余量已知时，该值由径向进给次数确定；δc为啮合点的压下量；δw为啮合点轮齿的总弯曲量。

剃齿刀单次径向进给量Δfr和啮合点的压陷量δc分别为[15]：

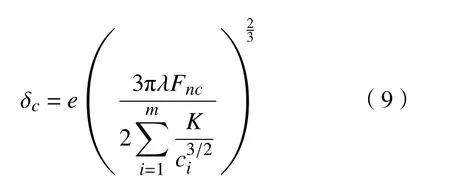
式中：Δ为剃齿切削余量；α为剃齿法向压力角；e为剃齿刀容屑槽槽距与槽宽之比；ci取决于两接触曲面主曲率大小及两主曲率方向之间的夹角；Fnc为啮合点垂直切削刃的作用力。

因为斜齿轮弯曲变形计算非常复杂，将工件齿轮简化为直齿变截面悬臂梁模型，如图2所示。假设齿轮左右齿面的啮合点分别为A和B，则啮合点A处的弯曲变形δw[16]为

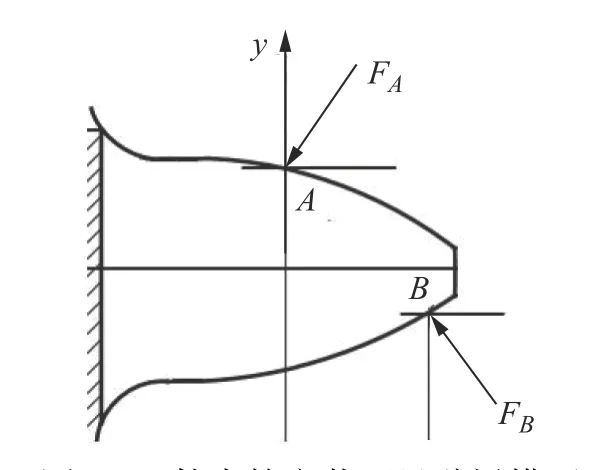
图2 工件齿轮变截面悬臂梁模型

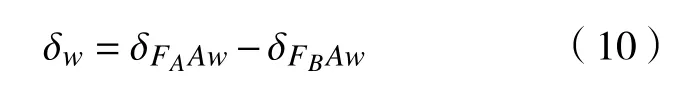
式中：δFAAw、δFBAw分 别为FA和FB沿y轴方向上的分力对A点的弯曲变形，FA、FB分别为啮合点A、B受到的剃齿径向力。

由于剃齿加工是无间隙的切削加工运动，中心距误差Δa会直接影响剃齿过程中的背吃刀量，根据空间几何关系可以求出剃齿加工背吃刀量误差Δap为

最终求得剃齿时每次径向进给的背吃刀量ap为

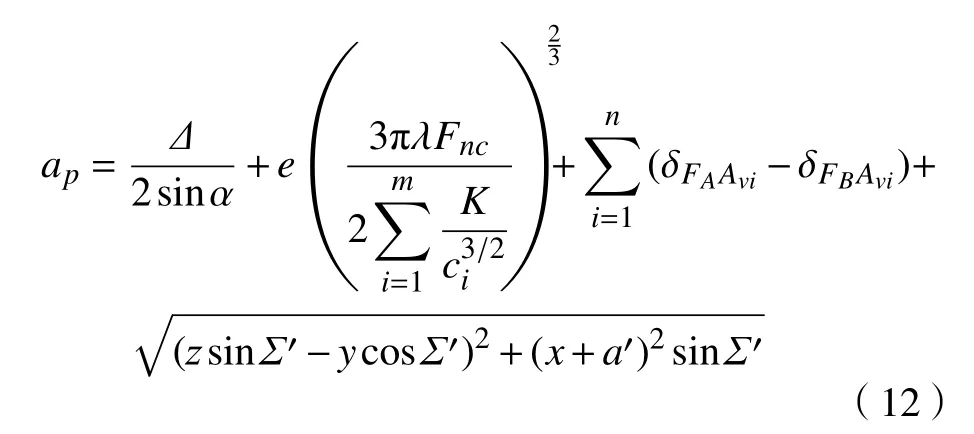
该模型由于同时考虑安装误差、相对滑移速度、诱导法曲率和背吃刀量，可以更全面地分析所有因素对剃齿加工的影响，为剃齿加工的多因素耦合打下基础。

2 齿形中凹误差预测模型

2.1 剃齿啮合点单次切削面积

重合度、安装误差和机床运动等因素均是影响剃齿齿形中凹误差的重要因素，基于剃削原理将这些因素耦合为单次切削面积，进而可以通过单次切削面积来研究多因素耦合对剃齿齿形中凹误差的影响规律。

根据剃削原理可知：剃齿是在单点啮合的同时对工件的侧表面进行刮剃加工，工件齿轮每转动一周剃齿刀在啮合点处进行一次切削加工，将这次切削加工定义为啮合点单次切削加工。考虑到剃齿各啮合点之间的切削要素完全不同，基于传统正交切削模型建立剃齿啮合点单次切削模型，其中单次切削的实体模型如图3a）所示，啮合点A经历的开始接触-背吃刀量最大-结束接触3种接触状态模型如图3b）所示。这3种接触状态对应的剃齿刀转角分别为φ1、φ2、φ3，单次切削面积指的是在啮合点单次切削加工中工件齿廓侧表面被剃除的面积。求解啮合点的单次切削面积，需推导出啮合点处实际背吃刀量a′p关 于诱导法曲率K、切削速度V1和剃齿刀转角φ 的函数。

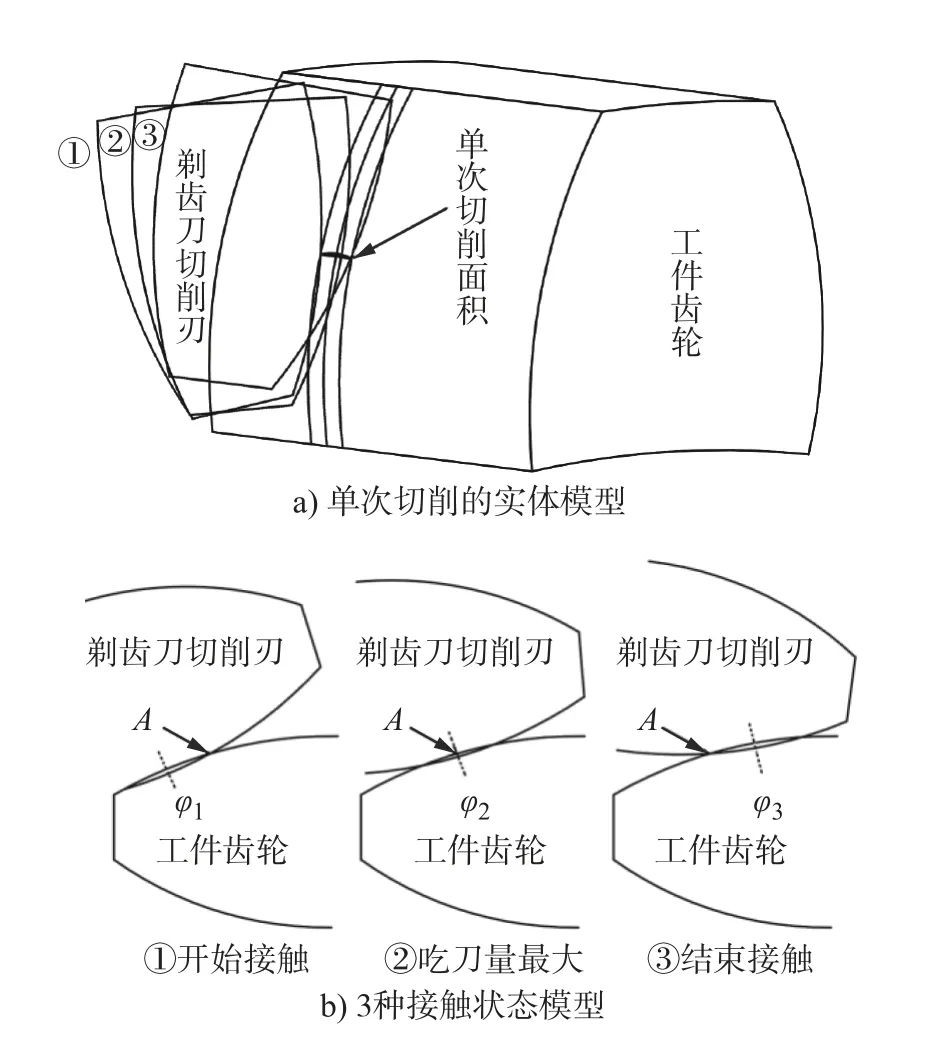
图3 剃齿啮合点单次切削模型

根据啮合点A在开始接触状态和结束接触状态的实际背吃刀量为0，可知剃齿刀转角φ1、 φ2、φ3之间满足：

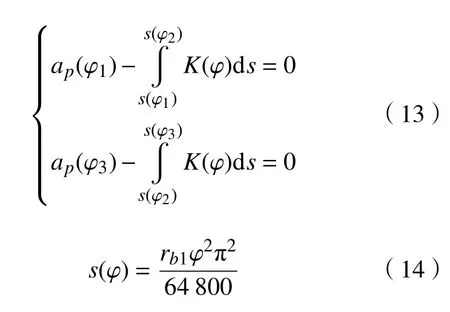
式中s(φ)为切削刃上啮合点距离剃齿刀齿根的弧长。

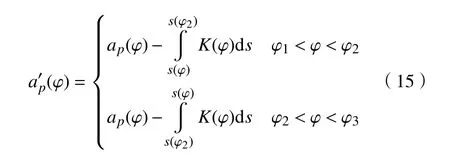
单次切削过程中的切削长度l为

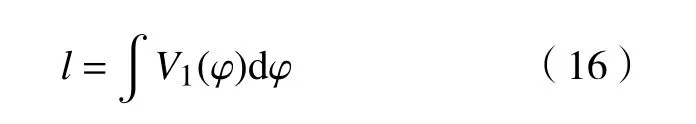
联立式（15）和式（16），得单次切削面积U为

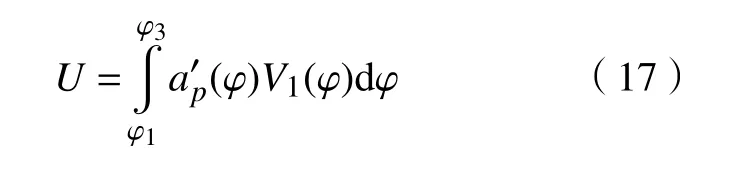
2.2 建立剃齿齿形中凹误差预测模型

在剃齿加工中，剃齿齿形中凹误差一般通过测量工件齿轮齿廓的形状偏差值来表示。齿廓的形状偏差是指在计量范围内，包容实际齿廓迹线的两条与平均齿廓迹线完全相同的曲线间的距离，既齿廓的形状偏差由实际齿廓轨迹上的最高点和最低点决定。考虑到啮合点单次切削面积与实际齿廓轨迹的深度成负相关，将啮合点单次切削面积的最大值和最小值作为影响齿廓形状偏差的关键因素，通过遗传算法改进BP神经网络（GA-BP）来建立剃齿齿形中凹误差的预测模型。

遗传算法改进BP神经网络（GA-BP）是通过遗传算法（GA）的搜索最优解功能来优化BP神经网络中初始神经元之间的权值和阈值的选择，其流程图如图4所示。

图4 遗传算法改进BP神经网络流程图

由于篇幅问题只对适应函数的计算进行详细说明。由于遗传算法搜索的是预测误差平方和最小的网络阈值和权值,且遗传算法只能朝适应度函数值越来越大的方向进化,故选择均方误差（MSE）的倒数作为适应度函数，则

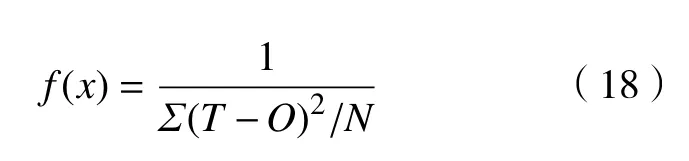
式中：f(x)为 适应度函数；T为期望输出；O为实际输出；N为输入样本数。

3 讨论及分析

3.1 模型验证

由于剃齿齿形中凹误差常发生在小模数齿轮和重合度小于2的剃齿加工中，根据齿轮手册[17]选取齿数为17、模数为4.2333、压力角为20°、变位系数为0.0468的小模数工件齿轮，并基于齿轮刀具设计与选用手册[18]选取4组不同重合度的剃齿刀，如表1所示。

表1 剃齿刀参数

根据齿轮手册[17]选定剃齿加工的主轴转速n范围为5.33 ～ 12.47 r/s，径向进给速度V径范围为3.3 ～5.8 μm/s，轴向进给速度V轴范围为0.43 ～ 1.21 mm/s，根据工程实际分别选取主轴转速为6 r/s、8 r/s、10 r/s、12 r/s、径向进给速度为3.3 μm/s、3.9 μm/s、4.5 μm/s、5.8 μm/s和轴向进给速度为0.5 mm/s、0.6 mm/s、0.85 mm/s、1 mm/s。假设中心距误差范围为0.01 ～0.06 mm，轴交角误差范围为0.1° ～ 0.7°，两个高速轴的同步误差范围为0.01 ～ 0.05 r/min，分别对机床的位移、角度和速度参数进行微调，并用微调参数来表示实际的安装误差。选取表1中的4组剃齿刀参数分别在YW423剃齿机上试剃工件齿轮，应用万能齿轮测量仪GM3040a对剃后齿轮进行齿形齿向检测，并采用相同微调参数对应的安装误差、剃齿刀参数以及机床运动参数来计算剃削过程中的单次切削面积。

为选取合理的样本，基于单一变量原则选用24组参数组合，通过加工实验得到24组工件齿轮左右齿面齿形中凹误差实测值及其中心位置齿廓展开角，考虑左右齿面的对称性，选取其中14组右齿面实验测量值作为预测模型的训练数据样本，剩余10组右齿面实验测量值作为模型的验证数据样本。

在MATLAB中建立剃齿齿形中凹误差预测模型，其中输入参数为单次切削面积的最大值Umax、最小值Umin和 最大值对应齿廓展开角 θmax，输出参数为剃齿齿形中凹误差值E和中凹误差中心位置齿廓展开角θ，隐含层节点数为10，训练步长为10000，目标误差设置为0.0001，学习效率为0.01。

表2为仿真预测值与实测值的对比误差，由表2可知中凹误差预测值与实测值的最大误差为9.35%、最大误差值为2.2 μm、平均误差为6.93%，中凹误差中心位置预测值与实测值的最大误差为3.89%、最大误差值为1.09°、平均误差为2.19%。对比结果说明预测模型对剃齿齿形中凹误差值和中凹误差中心位置具有较高的预测精度，验证了预测模型的可行性与准确性。

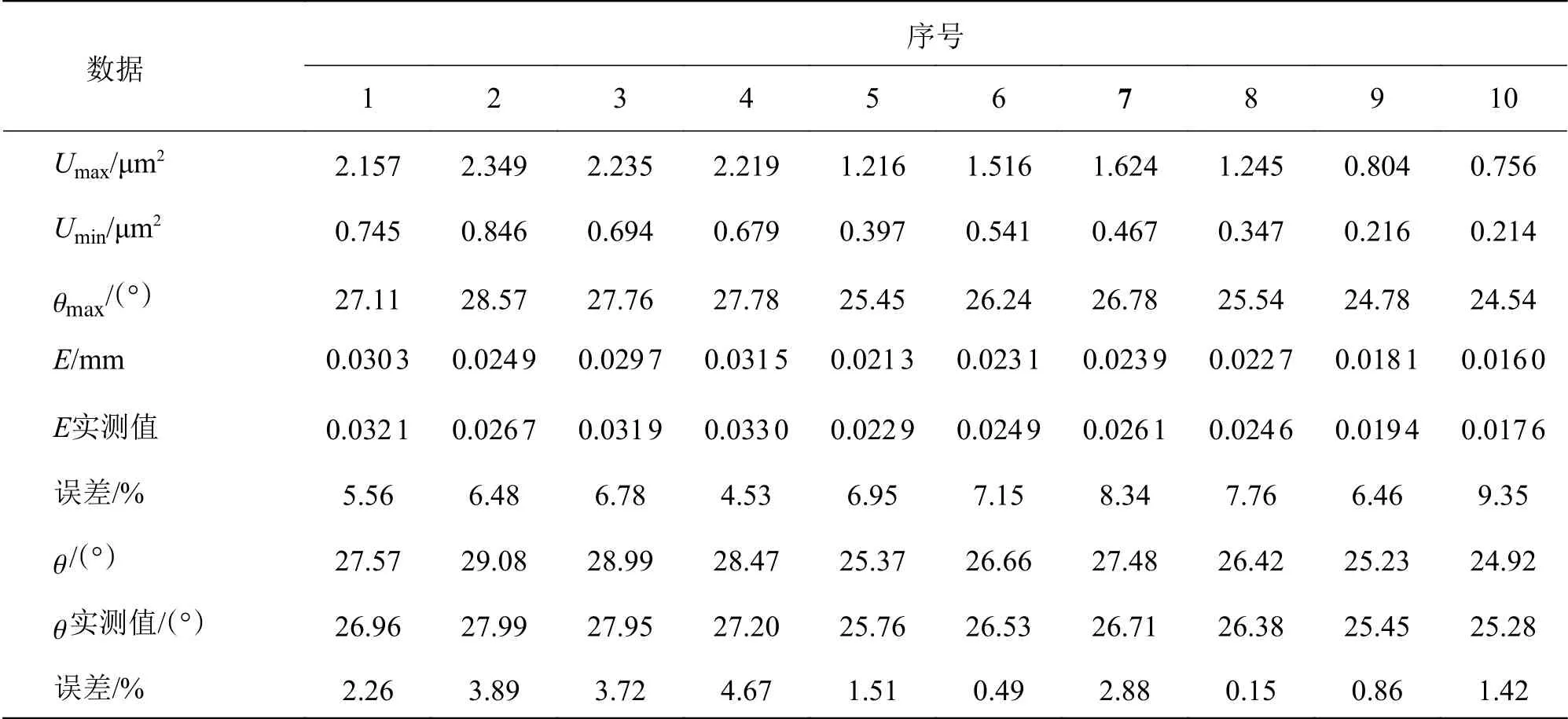
表2 仿真预测值与实测值的误差

3.2 单次切削面积对剃齿齿形中凹误差的影响

为了研究单次切削面积对剃齿齿形中凹误差的影响，对剃齿齿形中凹误差值及其中心位置随单次切削面积的变化规律进行了分析，如图5和图6所示。

图5表明，工件齿轮的齿形中凹误差随着单次切削面积的增大而增大，当单次切削面积超过一定值后齿形中凹误差减少。这说明了过量切削是剃齿齿形中凹误差形成的主要原因，且单次切削面积与中凹误差值关系曲线中存在极大值点，极大值点对应的剃齿齿形中凹误差值最大，故选取剃削参数时应该避免单次切削面积极大值点的出现。剃齿加工是多刀刃的重复切削，而每次切削加工产生的齿形中凹会导致中凹位置的诱导法曲率减小，即中凹位置后续的实际单次切削面积不断减小。当中凹位置的单次切削面积小于其两侧时，齿形中凹误差会产生修正现象，而中凹位置的初始单次切削面积越大，其后续单次切削面积的减小速度就越快，所以当初始单次切削面积超过一定值时会出现齿廓偏差的修正现象。

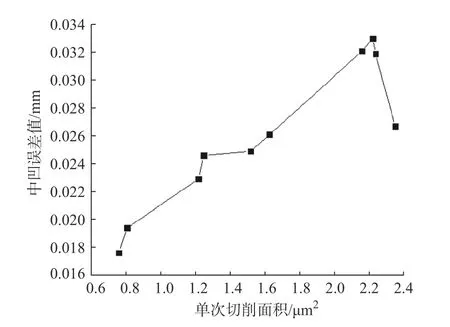
图5 单次切削面积与中凹误差值关系曲线

图6 表明，齿形中凹误差的中心位置与最大单次切削面积的位置基本重合，随着单次切削面积的增大其中心位置逐渐向齿顶移动。其原因为：最大单次切削面积的位置决定了中凹误差的中心位置；当啮合点径向力增加时，齿顶侧的弯曲变形增长速度比齿根侧的大，使得齿顶侧单次切削面积增长速度也偏大，导致齿面整体单次切削面积增大时最大单次切削面积的位置向齿顶移动。

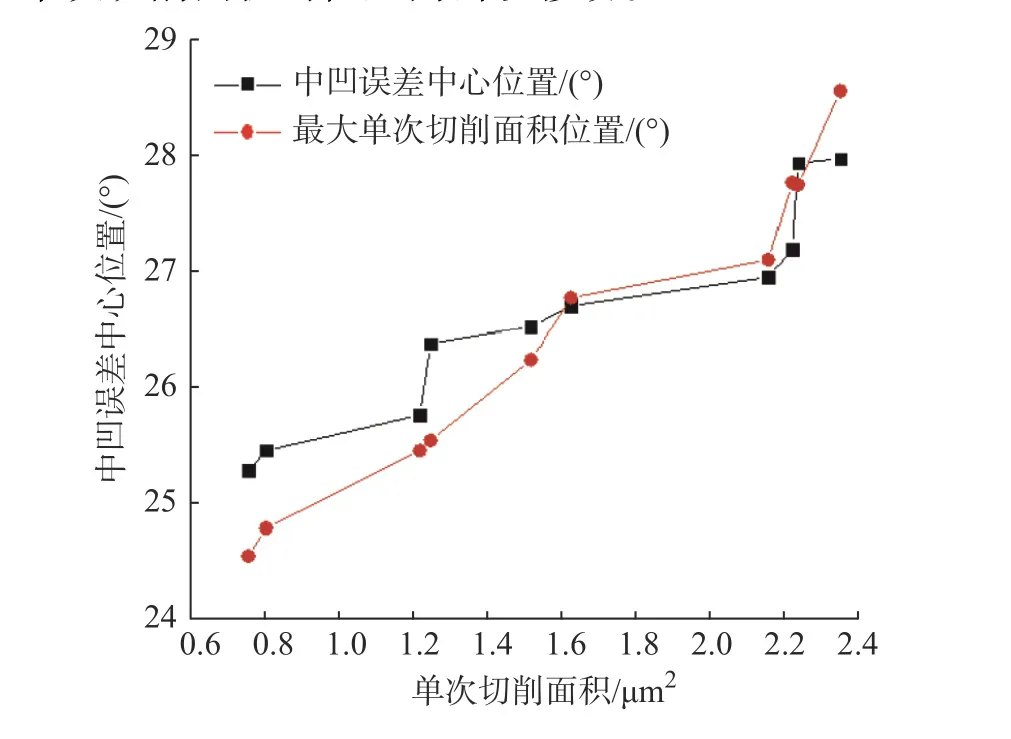
图6 单次切削面积与中凹误差中心位置关系曲线

3.3 切削参数对单次切削面积的影响

为分析各切削参数对单次切削面积的影响，基于单一变量原则选取12组切削参数计算得出最大单次切削面积，如表3所示。

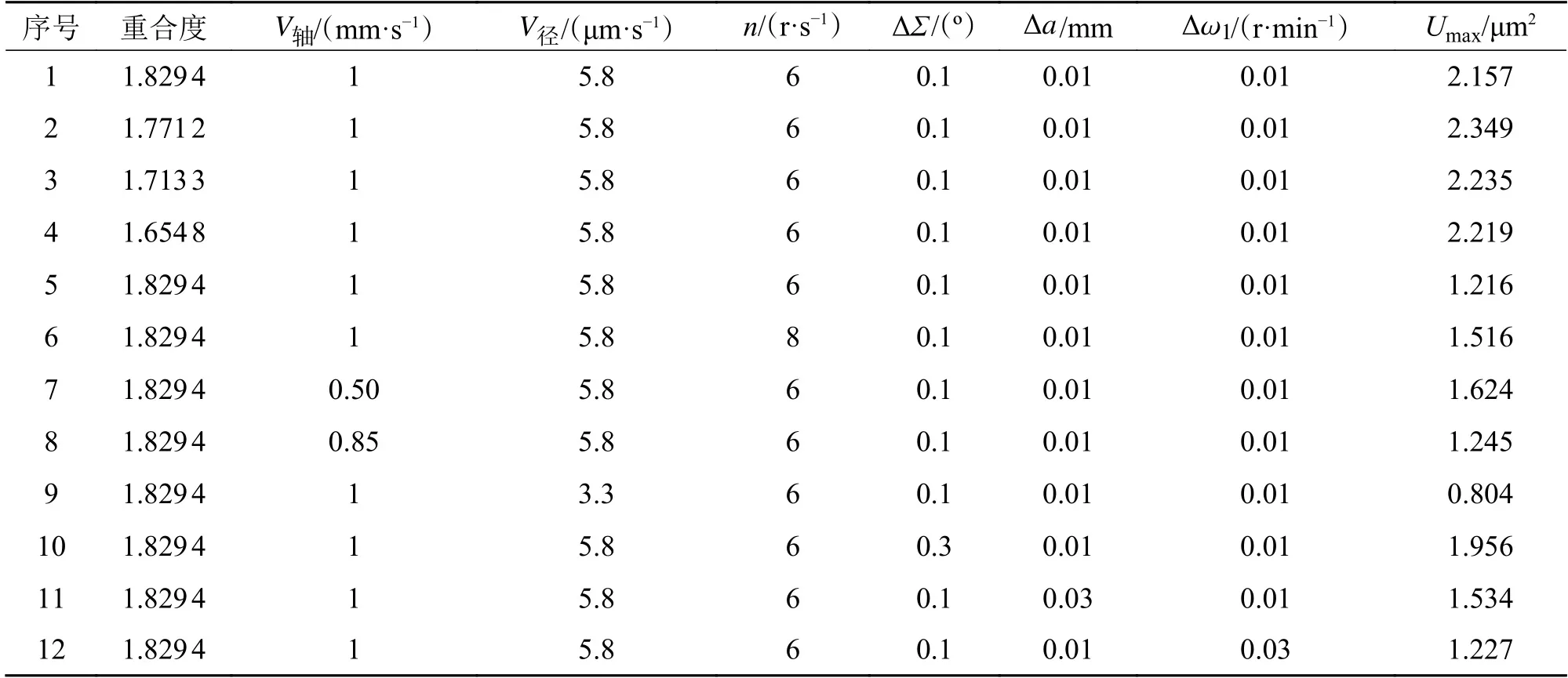
表3 不同切削参数的最大单次切削面积

当剃齿啮合的重合度从1.6548增加到1.7112时，单次切削面积减小；当重合度继续增加到1.8294时，单次切削面积增大。这是因为重合度的增大会导致诱导法曲率的减小和切削长度的增大，当重合度大于一定值时切削长度变化的影响要大于诱导法曲率变化的影响，即过大的重合度会导致单次切削面积增大，增大了剃齿齿形中凹误差。

剃齿的径向进给速度和轴向进给速度与剃齿单次切削面积成正相关，主轴转速与剃齿单次切削面积成负相关。这是因为径向进给速度越大，啮合点的背吃刀量越大，单次切削面积也就越大；轴向进给速度越大，啮合点的切削速度越大，单次切削面积也就越大；主轴速度越大，啮合点的相对滑移速度越大，单次切削面积也就越小。剃齿的轴交角误差、中心距误差和高速轴同步误差与剃齿单次切削面积成正相关，其中轴交角误差和中心距误差对剃齿单次切削面积的影响最明显，高速轴的同步误差对剃齿单次切削面积的影响几乎可以忽略。这是因为增加轴交角误差和中心距误差都会直接增加单次切削过程中实际的背吃刀量，导致单次切削面积快速增大。

4 结论

1）建立了同时考虑安装误差、相对滑移速度、诱导法曲率和背吃刀量的剃齿分析模型，基于剃削原理将剃齿加工过程中的多源因素耦合为啮合点单次切削面积，为剃齿加工多因素耦合分析提供了一种新方法。

2）通过遗传算法改进BP神经网络（GA-BP）建立了剃齿齿形中凹误差预测模型，预测结果与实验测试结果比较可知，剃齿齿形中凹误差预测值和中凹误差中心位置预测值的平均误差分别为6.93%和2.19%，验证了预测模型的可行性和准确性。

3）切削参数对剃齿单次切削面积有着直接的影响，可以通过增大重合度、主轴转速以及减小径向进给速度、轴向进给速度、轴交角误差和中心距误差等方式来减小剃齿的单次切削面积，达到控制剃齿齿形中凹误差的效果。

4）定量分析了剃齿齿形中凹误差的变化规律，发现单次切削面积过大是引起剃齿齿形中凹误差形成的主要原因，剃齿齿形中凹误差与单次切削面积成正相关，中凹误差的中心位置会随着单次切削面积的增大向齿顶移动。