基于用户偏好置信度的增强贝叶斯个性化排序算法

汪志远 石红瑞

(东华大学信息科学与技术学院 上海 200000)

0 引 言

在当今信息化时代，如何快速并且准确地获取信息显得十分重要。正是由于现代生活节奏的加快，人们总是希望在最短的时间内找到自己所需要的信息，于是推荐系统应运而生。推荐系统通过用户的行为反馈来推测用户对商品的喜好程度而加以推荐。在用户的反馈中，直接对商品给出评价分数的行为被称作显式反馈，如在豆瓣上给电影打分，在购物网站上给商品评级，这些行为在一定程度上能表达用户对商品的喜好程度。但是现实生活中的大多数数据并不是显式反馈数据，如用户对商品的点击、收藏、购买和评价等行为，它们都是隐式反馈行为，不能直接表达用户对商品的喜好程度。在隐式反馈中，只存在用户与商品已经发生过互动行为的正反馈信息，缺少没有互动过的负反馈信息。

对于显式反馈，一般的推荐算法有：基于内容的推荐、基于协同过滤的推荐[1-3]、混合推荐。这些推荐算法通过用户对商品的评分数据来预测用户对未购买商品的评分，从而产生推荐列表。由于隐式数据庞大且缺少用户对商品的直接评分，显式反馈推荐算法无法适用。为了解决隐式反馈推荐问题，文献[4]提出单类协同过滤算法，来解决协同过滤中只存在正样本缺少负样本信息的问题。经过后续对隐式反馈推荐算法的研究，有学者提出了基于隐式反馈的排序推荐框架，贝叶斯个性化排序(BPR[5])算法。作者通过假设用户对有互动行为的商品喜爱程度大于没有互动行为的商品，建立了贝叶斯模型。在此基础上，GBPR[6]提出用户的偏好会受到其他用户的影响，这些有着共同的偏好的用户可以归属到一个群组。

隐式反馈虽然不能直接表达用户对商品的偏好，但是其数据信息十分丰富。用户将商品加入购物车、购买商品和关注商品等行为，都表示用户对该商品有一定的兴趣度。本文在BPR算法的基础上，提出一种基于用户偏好置信度的增强贝叶斯个性化排序算法，通过对用户行为量化得到各反馈行为的权重，再根据用户反馈行为的类型和时间计算用户偏好置信度，在原排序模型中引入用户对发生互动行为的商品的偏序关系，提高推荐算法的效果。

1 BPR算法

BPR算法将商品集合划分成购买过的商品集和未购买过的商品集合，认为在这些隐式反馈商品集合中用户对有过购买行为的商品的喜爱程度大于没有购买过的商品。根据这一假设可以建立多组商品的偏序对>u，表示用户u对商品的喜好。在数据集中构造一系列三元组集合Du={(u,i,j)(或i>uj)}，其中：u属于用户集合U；i属于有购买行为的商品集合中的商品；j属于未购买过的商品集合中的商品；i>uj表示用户u相较于商品j更加喜欢商品i。

BPR算法中的模型参数为Θ，则优化模型为概率模型P(Θ|>u)，根据贝叶斯公式可以得到：

P(Θ|>u)∝P(>u|Θ)P(Θ)

(1)

假设各个用户对商品的偏序关系相互独立，且单一用户对不同商品的偏序关系相互独立，P(>u|Θ)有以下关系：

(2)

文献[6]使用一个函数来代替p(i>uj|Θ)：

(3)

其中：

(4)

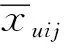
(5)

对P(Θ)进行贝叶斯假设，使其符合正态分布：

p(Θ)～N(0,λΘI)

(6)

式中：λΘ为特征值，I为单位矩阵，它们构成协方差矩阵。

文献[5]中使用矩阵分解[7]模型来训练参数Θ，假设X为用户对商品的评分矩阵，分解成用户矩阵Wm×k和商品矩阵Hk×n：

X=Wm×kHk×n

(7)

式中：m表示用户个数；n表示商品个数；k表示分解维度。模型的目标函数为：

(8)

式中：R(Θ)为正则项，防止产生过拟合现象。

2 EBPRC算法

2.1 用户行为量化

隐式反馈数据中，存在用户的多种反馈行为，如加入购物车、从购物车中删除、购买商品和收藏商品等，BPR算法通过购买商品集合和未购买商品集合来建立用户的偏好序列，忽略了用户的其他行为，这些数据没有得到很好的应用，导致该算法在多反馈行为下的推荐性能不高。

用户对商品的行为类型和次数能够在一定程度上表达用户对商品的喜爱程度。通过量化的方式来获取用户行为权重的分布，从而将多反馈行为量化成具体的数值Sui，数值越大，则用户与商品之间的互动行为越频繁，表明用户对商品的喜爱程度越高。量化后的Sui如下：

(9)

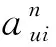
2.2 基于用户偏好的置信度

假设1用户行为量化后的Sui越大，置信度越大。

假设2用户行为的时间越近，置信度越大。

考虑到时间因素的影响，引入时间衰减函数：

(10)

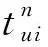
(11)

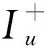
2.3 EBPRC模型

考虑到BPR算法的严格偏序关系，提出一种基于用户偏好置信度的增强贝叶斯个性化排序算法(Enhanced BPR with Confidence，EBPRC),对排序模型进行增强。

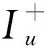
>u=λxupq+(1-λ)xuij

(12)

式中：λ用来平衡不等式优化结构的参数，具体数值根据模型在数据集中的推荐效果而定[8]。用户和商品整体的极大似然式可以表示为：

EBPRC(u)=P(>u)

(13)

同样地，用σ(x)来替代P(x)，则EBPRC对数似然估计为：

(14)

模型的目标函数为：

(15)

式中：R(Θ)为正则项，用来抑制过拟合。BPR算法使用矩阵分解求解参数模型Θ，类似地引入矩阵分解模型，并在原来的基础上引入偏置项b，分解模型如下：

xul=WuHl+bl

(16)

式中：Wu为用户特征向量;Hl为商品特征向量。R(Θ)按照文献[6]的处理：

(17)

f(u,L)=ln(1+exp(->u))+

(18)

2.4 模型训练

利用随机梯度下降法对目标函数进行优化，求目标函数在参数θ的梯度，其中θ∈{Wu,Hl,bl|l∈L}，计算如下：

(λ(Hp-Hq)+(1-λ)(Hi-Hj))+αuWu

(19)

(20)

(21)

得到模型在各参数方向的梯度后，模型通过随机梯度下降法更新参数，计算如下：

(22)

式中：γ为迭代时的学习率。训练模型时，随机从用户集合U中挑选出一个用户u，从集合Du中随机挑选出一个偏序对(u,i,j)，从集合Mu中随机挑选出一个偏序对(u,p,q)，得到一组反馈集合，更新模型参数θ，反复迭代一直到模型收敛。根据最后返回的参数模型，计算出用户对各商品的评分，然后对评分进行排序，挑选评分较高的商品推荐给用户，达到个性化推荐的目的。

模型训练算法如算法1所示。

算法1EBPRC训练算法

输入：用户集合U，偏序对集合D和M，矩阵分解维度k，模型参数θ。

输出：模型收敛后的参数θ。

1.初始化参数θ；

2.从集合U中随机挑选一个用户u；

3.从Du中随机挑选一个偏序对(u,i,j)；

4.从Mu中随机挑选一个偏序对(u,p,q)；

5.根据式(19)-式(22)更新参数θ；

6.重复步骤2-步骤5，直到模型收敛。

7.返回参数θ

3 实 验

3.1 数据集

本次实验采用的是京东算法比赛数据集，该数据集包含了2016年2月1日到2016年4月15日用户对不同商品的6种隐式反馈行为。这些反馈行为包括浏览、加购(加入购物车)、删购(从购物车中删除)、下单、关注和点击。数据集中包含用户对商品发生的行为类型和发生行为的具体时间。原数据集包含了50 601 736条行为记录，其中存在一定的数据冗余，因此需要数据预处理。通过数据统计发现点击行为占所有反馈行为的比重为60.5%、浏览行为所占比重为37.5%，因此，认为这两种反馈行为对实验的影响较小，不考虑这两种反馈行为。原数据集稀疏程度大，为了方便后续推荐性能的评价，从数据集中过滤掉购买次数少于10的用户和被购买次数少于5的商品。经过处理后的实验数据格式如表1所示，其中行为类型0、1、2、3分别表示加购、删购、下单、关注。将数据集切分成训练集和测试集，具体切分方式：根据时间节点切分[9]。本实验的数据集时间横跨75天，按照2 ∶1切分数据集，前50天的数据为训练数据，后25天的数据为测试数据，也就是通过用户前50天的行为记录预测用户在后25天购买的商品。

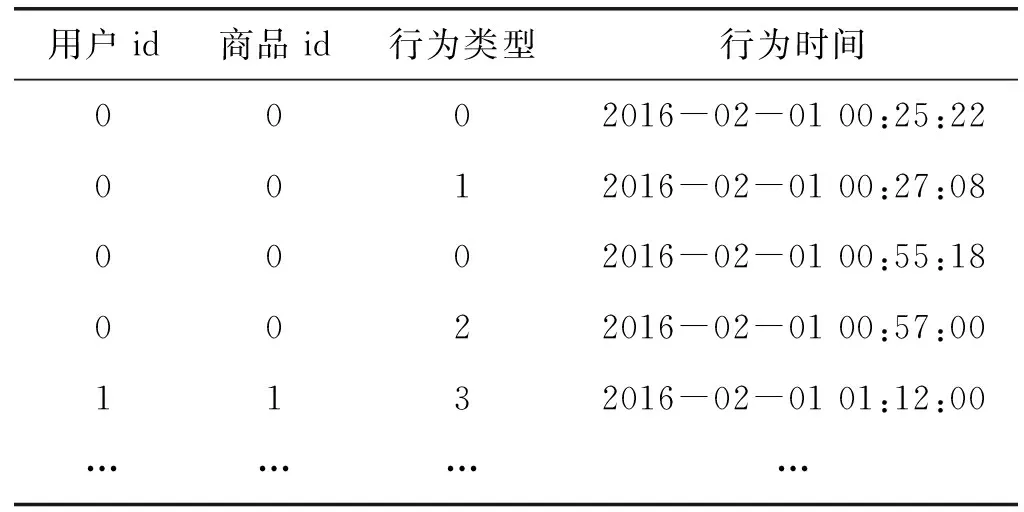
表1 用户行为反馈数据集

3.2 评价指标

采用TopN推荐算法和排序推荐算法对本文提出的推荐算法性能进行分析。对于TopN推荐，通过准确率、召回率和AUC值进行评估[10]。推荐算法为用户产生一个按照评分排序的推荐列表，取其中评分最高的N个商品推荐给用户，其中有多少比例是用户实际购买的，即为准确率(Precision@N)。同样地，推荐列表中用户实际购买的商品数量与用户购买的所有商品数量的比值为召回率(Recall@N)[11]。AUC值是ROC曲线下的面积，它用于衡量推荐模型将用户喜欢的商品和不喜欢的商品的区分程度，取值范围为0～1，值越大说明推荐模型越好。对于排序推荐，采用的推荐指标为平均准确率(MAP@N)，其值越大，用户喜欢的商品排序就越靠前，表明推荐性能越好。AP@N表示推荐列表中每个商品在排序位置的准确率的平均值，MAP@N为AP@N在用户粒度上的平均。

3.3 用户行为权重分布

本次实验需要将用户的四种反馈行为进行量化，将客观赋权方法中的熵权法和主观评价方法中的序关系分析法相结合组合赋权。

(1) 熵权法。客观赋权方法中的熵权法是指标权重获取的重要手段之一。设xij为用户i进行j种行为的总次数，则将其标准化的结果如下：

(23)

式中：i∈{0,1,…,n-1},n为用户个数；j属于四种行为类型中的一种，即j∈{0,1,2,3}。计算第j种行为的信息熵Ej：

(24)

(25)

根据信息熵计算行为权重：

(26)

(2) 序关系分析法。为了考虑实际情况下，用户行为类型对用户偏好程度的影响，利用主观评价方法中的序关系分析法通过从主观上判断用户行为类型的重要程度来进行权重计算。主观认为，从购物中删除行为表明用户不打算购买该商品，很大程度上是一种负反馈行为，因此重要程度最低；下单行为最能表示用户对商品的喜好，重要程度最高；加入购物车行为和关注行为也能表明用户的偏好。设Aj表示第j种行为类型的重要程度，则根据上面判断有：

A2>A0>A3>A1

(27)

假设存在下面的序关系：

(28)

(29)

rk的值可以参照表2。

表2 rk赋值对照表

根据表2得到下面的权重关系：

w2/w0=r1=1.2

w0/w3=r2=1.4

w3/w1=r3=-1.2

(30)

式中：r3取负值，因为删购行为是负反馈行为，关注行为是正反馈行为。

(3) 组合赋权。为了综合客观评价和主观评价的特点，利用组合赋权的方法确定最终的权重分布，计算如下：

(31)

表3 用户行为反馈量化后的权重分布

3.4 实验结果与分析

在本次实验中，用户反馈时间标准化后为时间戳，单位为ms，原数据集中用户重复的行为都有一定时间延迟，为了抑制时间因子对算法的影响，α=1 000×3 600，这样时间的最小单位从ms扩大到h。在模型的迭代过程中，矩阵分解维度k=20，学习率γ=0.01，正则化系数αu=αh=βh=0.01。在{0,0.1,0.2,…,1}中寻找最好的平衡参数λ[8]，根据评价指标MAP@N来确定最终的λ值，其结果如图1所示。

图1 平衡参数λ对评价指标MAP@N的影响

根据图1发现λ=0.3时MAP指数最大，选择这个平衡参数对模型进行训练，通过调整时间衰减系数α的大小探究时间衰减单位对推荐算法的影响，通过MAP@N来寻找合适的时间衰减单位，其结果如图2所示。

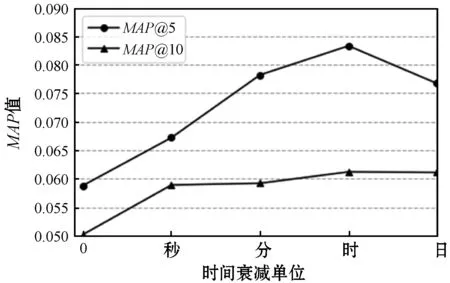
图2 时间衰减单位对评价指标MAP@N的影响

根据图2可知时间衰减单位为时的时候，推荐算法的性能最好，即α=1 000×3 600。选择最佳参数α和λ训练模型，将训练后的结果与BPR算法和GBPR算法进行比较，结果如表4所示。

表4 各算法的性能指标

根据表4的实验结果可以发现，本文提出的EBPRC各项性能指标均有提升。特别地，准确率Pre@5较BPR算法提升了34.6%，较GBPR算法提升了21%，说明EBPRC算法有不错的准确率和预测质量。MAP@5较BPR算法提升了36.6%,较GBPR算法提升了15.4%，表明EBPRC算法的排序推荐性能显著。

4 结 语

本文先介绍了推荐算法中的隐式反馈推荐问题，并介绍了贝叶斯个性化排序推荐框架。基于BPR框架提出一种基于用户偏好置信度的增强贝叶斯个性化排序算法，通过对用户行为量化得到各反馈行为的权重，再根据用户反馈行为的类型和时间计算用户偏好置信度，根据置信度大小建立用户对发生互动行为的商品的偏序关系，并与原模型中的偏序关系相结合，训练模型。通过在多行为反馈数据集上的仿真实验，将本文算法与相关的基线算法BPR和GBPR相比较。

实验结果发现本文算法在AUC值、Precision@N、Recall@N、MAP@N等性能评价指标上有着不错的效果，较相关算法有显著的提升。在实验中，用户偏好置信度的建立受到很多因素的影响，比如用户行为反馈的量化方式、时间衰减的方式，这些都是需要在后续研究中去探讨。