不同捻制类型多层结构钢丝绳股力学性能对比研究

陈原培，秦 玮，何义团

(1. 重庆交通大学 交通运输学院，重庆 400074； 2. 重庆交通大学 航运与船舶工程学院，重庆 400074)

0 引 言

钢丝绳具有弯曲柔韧性强、轴向承载能力大、工作性能稳定等优点，通常被用作塔吊、斜拉桥、起重机等工程结构的关键部件。在复杂的服役环境中，钢丝绳受载形式多种多样，这导致其在工作中容易发生服役性能退化甚至失效报废，进而可能引起重大工程事故。因此为保障安全生产，探究钢丝绳服役性能尤为重要。

对于钢丝绳服役性能，国内外学者进行了广泛的研究。G.A.COSTELLO[1]提出了钢丝绳理论，该理论包含了钢丝绳的结构、摩擦特性、静力学特性等内容，为钢丝绳研究提供了重要理论参考；兰成民等[2-3]建立了钢丝绳疲劳寿命模型，推导了钢丝疲劳破坏循环次数，并在此基础上提出了疲劳寿命极限估计方法；张德坤等[4]对6×19提升钢丝绳的摩擦磨损性能进行了研究；E.Z.XING等[5]研究了钢丝绳在微重力和零张力影响下的弯曲特性；W.G.JIANG[6]建立了具有精确弯曲对称边界条件的简单钢丝绳有限元模型，并验证了其正确性；马军等[7]通过对不同捻距的钢丝绳进行有限元仿真，得出了捻距倍数对钢丝绳应力的影响规律；李红等[8]基于钢丝波导频散曲线，结合有限元方法分析了钢丝模态转角受拉力影响的变化规律；D.G.WANG等[9]针对1×19及6×19+IWS的多层结构钢丝绳进行了有限元仿真，分析了两类钢丝绳的疲劳寿命；张奔牛等[10]通过钢丝的应力和振荡频率间的关系检测钢丝中的预应力程度；L.LIU等[11]采用分层计算和直接计算两种计算模式对7×7钢丝绳股的力学性能进行了评估，其结果表明初始螺旋角对钢丝绳拉伸及扭转性能有显著影响；陈原培等[12]通过有限元分析，对不同类型钢丝绳的拉伸及扭转性能差异进行了探讨，并基于半解析法对变载荷钢丝绳进行了全接触分析，继而分析了绳间接触对钢丝绳力学性能的影响。

综上可知，学者们对钢丝绳服役性能进行了诸多研究。然而对于已被广泛应用的多层结构钢丝绳，由于其空间捻制的多样性与复杂性，不同捻制类型的钢丝绳间存在何种性能差异，以及该差异对其应用具有何种影响等问题，以往研究很少涉及。对此，笔者以具有多层结构的单股钢丝绳(简称：多层结构钢丝绳股)为研究对象，考虑钢丝弹塑性、丝间摩擦和接触等影响因素，建立交互捻多层结构钢丝绳股和同向捻多层结构钢丝绳股的参数化几何模型和有限元模型，探究两类绳股在拉伸载荷作用下的性能差异，以期为钢丝绳的设计与选用提供一定参考。

1 理论建模

1.1 多层结构钢丝绳股参数化几何模型

多层结构钢丝绳股复杂的空间结构影响其服役性能，为对绳股力学性能进行分析，精确建模十分重要。

建立了由芯丝(简称：CW)、内层侧丝(简称：IW)和外层侧丝(简称：OW)组成的两类多层结构钢丝绳股，其几何结构如图1。交互捻多层结构钢丝绳股芯丝为mC根直径为DC的直钢丝，内层侧丝为mI根直径为DI的钢丝以βI(约定右捻时捻角为正值，左捻时捻角为负值)的捻角捻制而成，外层侧丝则由mO根直径为DO的钢丝以βO的捻角捻制而成，且内层与外层侧丝捻向相反；同向捻多层结构钢丝绳股除外层侧丝捻向与交互捻绳股相反外其他所有几何参数均与交互捻绳股相同。

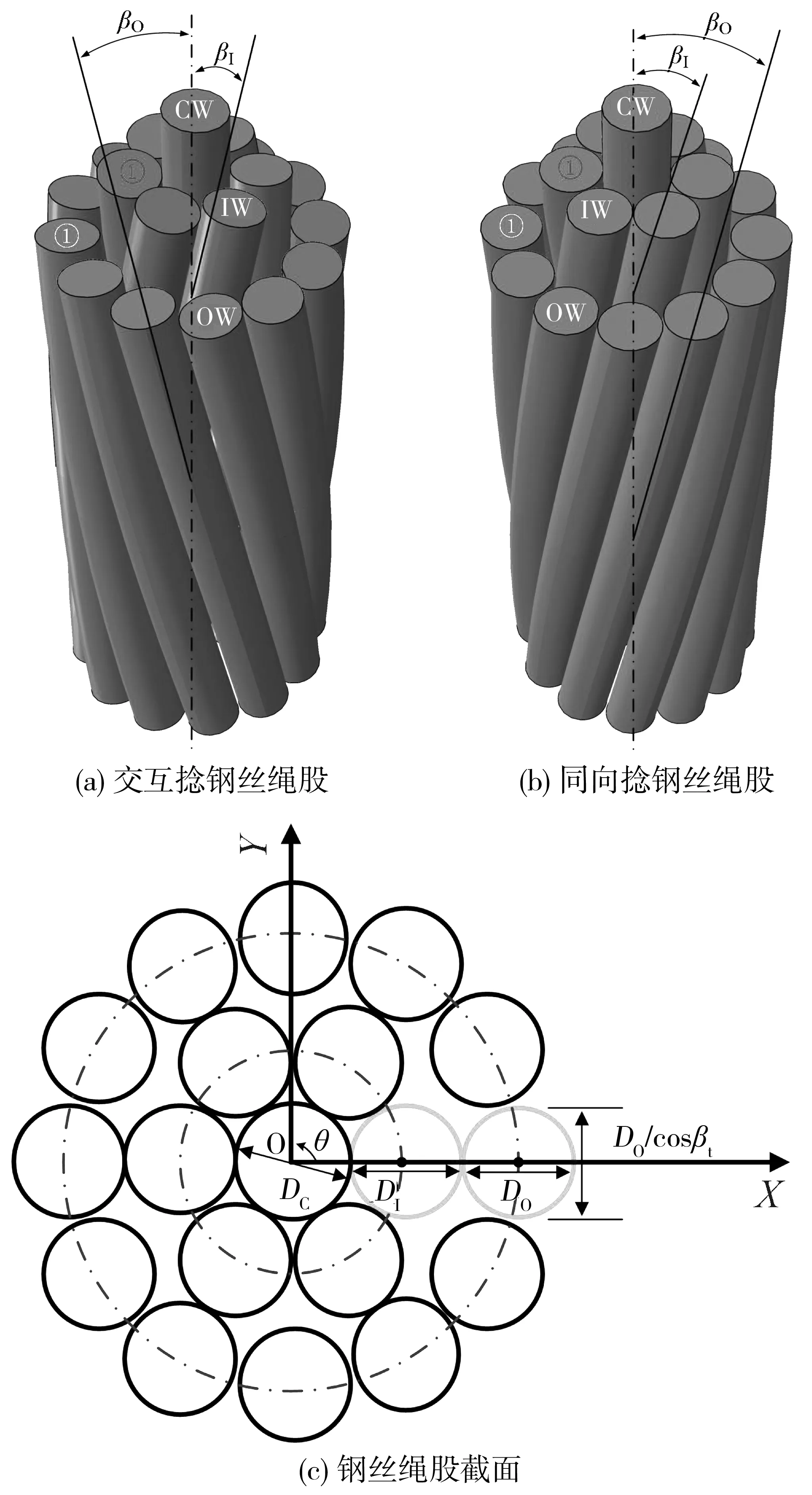
图1 多层结构钢丝绳股几何特征

建立原点为芯丝圆心的笛卡尔直角坐标系，使钢丝绳股的轴线方向为Z轴，X和Y轴如图1(c)。投影XY平面，则投影坐标(0，0)为芯丝中心，内层和外层侧丝在XY平面上的投影则为椭圆，其长轴和短轴分别为at=Dt/cosβt和bt=Dt(t=I或O)。因此，两类绳股侧丝空间曲线方程为：

Xtj=rtcosθ

(1)

Ytj=rtsinθ

(2)

Ztj=rtθtanβt+(j-1)st

(3)

式中：θ为绕绳轴的周向坐标；j为各层螺旋侧丝的标号，即j=1,2,3…,mt，其中mt为侧丝数(t=I或O，内层侧丝数mI=6，外层侧丝数mO=12)；rt为侧丝轴线螺旋半径，其中rI=(DC+DI)/2，rO=DI+(DC+DO)/2；βt为各侧丝的捻角；st=2πrcotβt/mtv为邻近侧丝的轴向距离(t=C或I)。

通过上述推导的参数方程，使用Pro/E软件建立交互捻多层结构钢丝绳股和同向捻多层结构钢丝绳股的参数化几何模型。笔者假定两类绳股的初始接触仅为径向接触(即CW-IW接触和IW-OW接触)而无周向接触(即IW-IW接触和OW-OW接触)，此处初始接触表示只发生接触但并未任何接触应力。为此，各几何参数需满足以下条件[13]：

(4)

(5)

合理的钢丝绳股模型长度是对其进行分析的重要环节，过大的模型长度将增加计算负担而显著降低求解效率，模型长度过短将引起终端效应而影响分析结果的准确性。因此，为保证仿真分析的计算效率和精确度，笔者使用W.G.JIANG[6]的方法，以多层结构钢丝绳股1/6的最大捻距作为绳股股长L，本研究中取股长L为45 mm。表1为两类绳股几何参数。

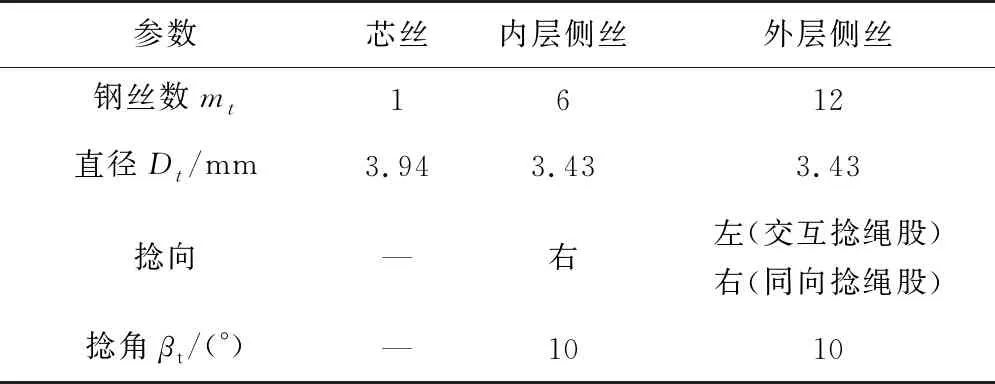
表1 多层结构钢丝绳股几何参数

1.2 多层结构钢丝绳股有限元模型

在1.1节建立的两类多层结构钢丝绳股几何模型的基础上，通过ABAQUS建立绳股的有限元模型。绳股材料特性参数为[6,14]：杨氏模量E=188 GPa，塑性模量EP=24.6 GPa，泊松比γ=0.3，屈服应力σY=1.54 GPa。此外，假定钢丝材料为各向同性，则根据材料强化准则可得屈服函数f：

f=σVM-h(εP)

(6)

式中：h(εp)为屈服强度函数；εp为累积等效塑性应变；σVM为von Mises应力，假定钢丝材料均符合双线性硬化准则，则h(εp)为[12]：

(7)

本研究采用ABAQUS进阶算法并以C3D8R八节点六面体单元进行绳股的网格划分，线性缩减积分适用于塑性、蠕变、大挠度等工况，能更好地模拟大变形[15]。图2为两类绳股网格划分结果。

图2 多层结构钢丝绳股网格模型

如前所述，在多层结构钢丝绳股模型建立时考虑了径向初始接触。而同层钢丝间的周向接触在加载过程中也可能发生。因此在罚函数Augmented-Lagrangian算法的基础上对丝间接触压力进行迭代求解，接触压力P为：

(8)

式中：sz为判断丝间是否发生干涉的接触间隙，其为负值则发生干涉，反之则未干涉；γz为用于增强计算效果的额外因子；Kz为接触刚度。丝间摩擦剪切力Ff可由Coulomb摩擦定理得到：

Ff=μP

(9)

式中：μ为摩擦系数，笔者取0.115[6]。另外，各节点处平衡方程为：

Fn=ku

(10)

式中：Fn、k和u分别为节点力矩阵、总刚度矩阵和节点位移矩阵。

考虑到多层结构钢丝绳股丝间复杂的多种接触状态，笔者将硬接触作为接触设定，以主从接触算法进行接触面间传递载荷。多层结构钢丝绳股进行拉伸有限元分析时，分别在钢丝绳股两端面创建参考点RP-1和RP-2，并分别与其所对应的端面进行运动耦合，再约束其6个自由度，并以逐步加载的方式对绳股模型进行加载。具体加载方式为：完全固定两类多层结构钢丝绳股的参考点RP-2，并将RP-1关于Z轴的旋转自由度UR3进行约束，对RP-1施加以0.001为步长，最大为0.01的沿Z轴的拉伸应变，其余自由度不做约束。图3为约束及加载方式。

图3 多层结构钢丝绳股约束及加载示意

2 模型有效性验证

分别对两类绳股进行几何模型和有限元分析模型的校核。首先，为确保绳股几何模型满足前文所述的丝间初始接触条件，通过Pro/E软件几何干涉工具进行检查。对于有限元模型，通过对绳股进行拉伸仿真分析，并与G.A.COSTELLO[1]弹性理论结果和D.G.WANG等[9]的分析结果进行对比的方式验证。由于两类绳股的加载和约束施加方式相同，在此仅选取同向捻多层结构钢丝绳股来进行验证。

2.1 网格灵敏度分析

有限元分析结果受到网格密度的直接影响，低密度网格不能保障精确度；高密度网格精度高，但将显著增加计算时间和资源，因此合适的网格密度十分必要。对此，笔者以交互捻多层结构钢丝绳股有限元模型为例进行了网格灵敏度分析。绳股加载和约束方式与图3相同。表2为3种不同网格密度下得到的轴向力FN、扭矩MN和von Mises应力，表2中还给出了各密度网格相对于最大密度网格的相对误差。

由表2可知，仿真结果受到网格密度影响，各结果数值随着网格密度的增大，而趋于平稳。网格密度越高所得结果越精准，但计算负担也随之增加。对比表2结果可知，b类网格所有结果值相对误差均不超过2%，在合理误差范围内，因此笔者以该密度网格进行两类绳股的拉伸有限元分析。

表2 网格灵敏度分析

2.2 结果对比

为验证中有限元模型，笔者采用的钢丝几何参数如表3。此外，股长L=9 mm，钢丝弹性模量E=203 GPa，泊松比为γ=0.3，塑性模量EP与文献[9]相同。验证结果对比如图4。

图4 多层结构钢丝绳股有限元模型验证

表3 验证模型几何参数

结果表明：本模型纯弹性结算结果与G.A.COSTELLO弹性理论一致；在考虑钢丝弹塑性后，本模型计算结果与D.G.WANG等[9]的结果十分吻合，拉伸应变达到0.007后绳股将发生塑性变形，弹塑性计算结果低于弹性计算结果。由上述可知，笔者所建立的多层结构钢丝绳股有限元模型准确有效。

3 结果与讨论

在笔者所建立的交互捻和同向捻多层结构钢丝绳股有限元模型基础上，分别对其进行拉伸有限元仿真，并分析两者的性能差异及其在实际应用产生的影响。图5为交互捻和同向捻多层结构钢丝绳股在轴向拉伸载荷下的结果对比。其中，轴向力值为正表示其为沿Z方向拉伸，反之则为沿Z方向压缩；扭矩值为正表示关于绳股轴线方向的扭矩与右旋方向一致，反之则相反。由图5可知，拉伸初始阶段，两类绳股的轴向力和扭矩随着拉伸应变的增加近似线性增加，且均未发生塑性变形；当拉伸应变达到0.006左右时，丝间接触发生了应力屈服，产生了塑性变形，轴向力和扭矩增加速率降低。由图5(a)可知，同向捻绳股的扭矩方向与其右捻向相同，而交互捻与左旋方向一致且绝对值比同向捻绳股小，表明交互捻钢丝绳股受拉伸载荷时具有更好的抗旋转性能。

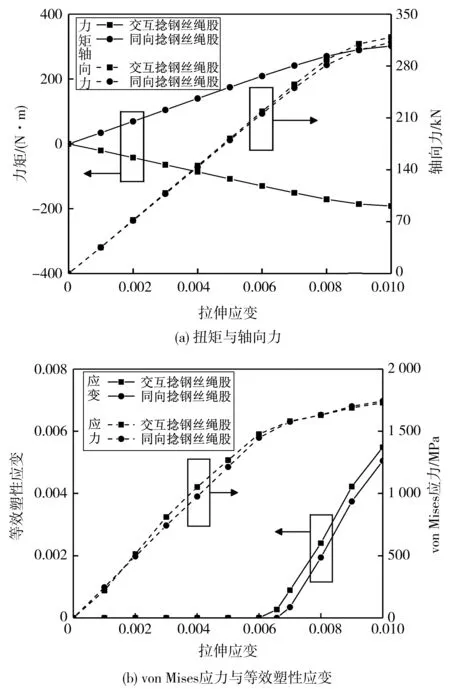
图5 交互捻钢丝绳股和同向捻钢丝绳股拉伸性能对比

由图5还可知，拉伸加载结束时，交互捻和同向捻绳股最终von Mises应力差值并不大，可见两类多层结构钢丝绳股的整体应力受拉伸载荷影响相近。0.01拉伸应变时，交互捻绳股产生塑性应变比同向捻绳股更大，表明交互捻绳股更易发生应力屈服。

图6为交互捻和同向捻钢丝绳股应力应变分布。由图6可知，拉伸载荷下，两类绳股的丝间接触状态相同，即芯丝-内层侧丝接触和内层侧丝-外层侧丝接触，两类接触产生的应力均以60°角为周期呈圆周对称式分布。等效塑性应变分布规律与应力分布规律一致，对比应变分布可知，交互捻绳股在内层侧丝-外层侧丝间的接触位置产生最大塑性应变，而同向捻绳股在芯丝-内层侧丝间接触部位发生，且前者大于后者。上述区别的原因在于交互捻绳股内层和外层侧丝的捻向不同，二者丝间点接触产生了比芯丝-内层侧丝间线接触更大的接触应力，因而产生更大的塑性应变。

图6 拉伸载荷下交互捻钢丝绳股和同向捻钢丝绳股应力应变分布

为进一步探讨交互捻和同向捻绳股服役性能差异，笔者对比分析了两类绳股局部性能参数。

图7为两类绳股von Mises应力和等效塑性应变沿绳股径向，即图1(c)中X轴方向结果对比。由图7可知，两类绳股的von Mises应力和等效塑性应变沿绳股径向变化趋势相似。交互捻绳股在绳股芯层产生的应力和塑性应变小于同向捻绳股。两类绳股的应力应变值均沿径向逐渐增加，并在芯丝-内层侧丝(CW-IW)接触位置达到第1个峰值。随着径向距离的进一步增大，交互捻绳股在内层侧丝的结果先减小后增大，并在内层侧丝中部达到局部最小，在内层侧丝-外层侧丝(IW-OW)接触处达到最大值；而同向捻绳股在内层侧丝的结果逐渐减小，并在IW-OW接触处达到最小值。上述现象发生的原因在于，交互捻绳股不同的内外层侧丝捻向，从而以点接触形式产生钢丝内部应力，导致拉伸过程中CW-IW接触点应力与IW-OW接触点结果相当，进而在内层侧丝芯部形成低应力区；对于同向捻绳股，内外接触点产生的应力相差较大，使内层侧丝产生沿径向方向的递减应力区。由图7还可知，等效塑性应变的变化趋势与应力变化趋势相对应，交互捻绳股塑性变形最大发生在IW-OW接触部位，而同向捻绳股发生在CW-IW接触部位。

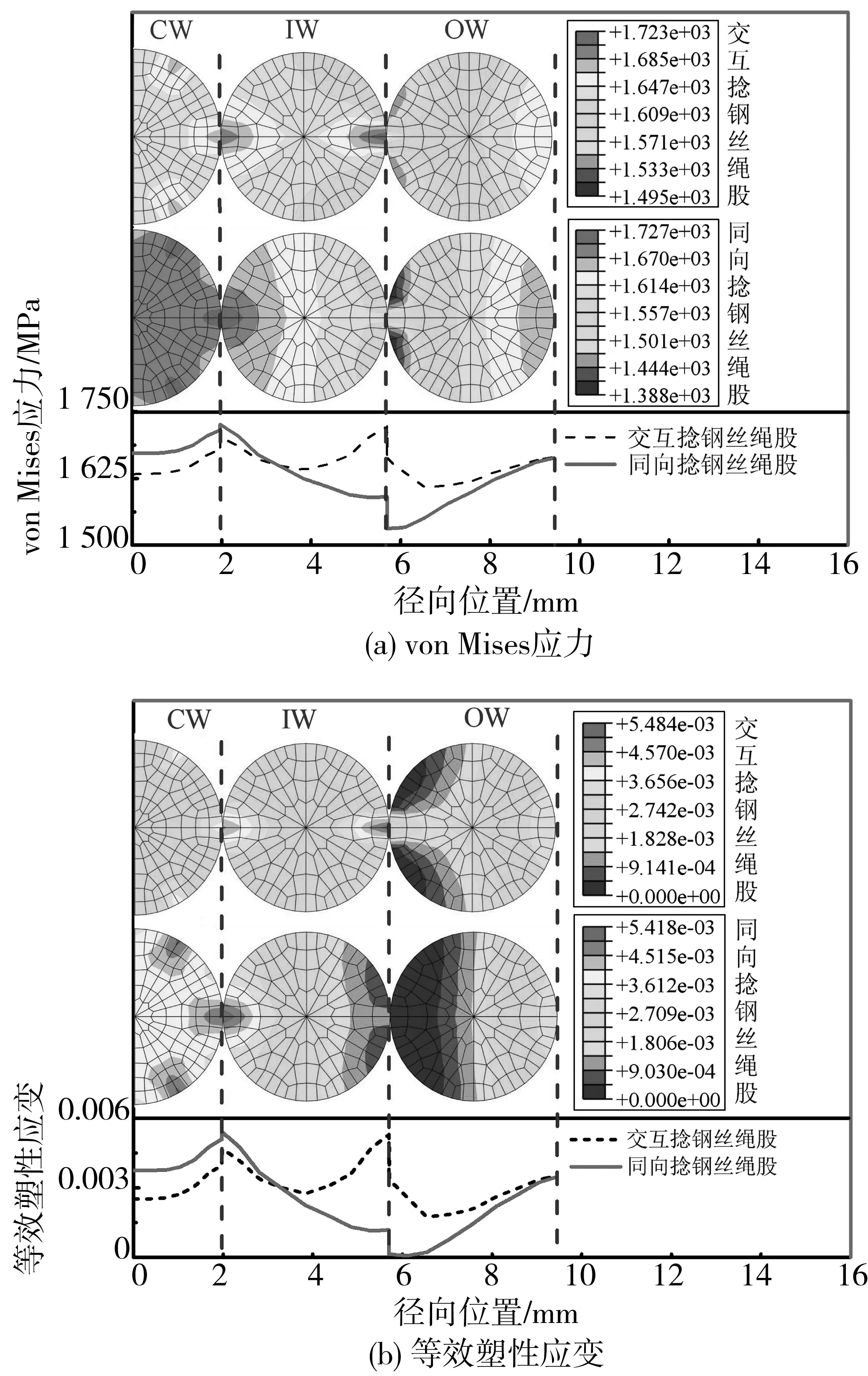
图7 交互捻钢丝绳股和同向捻钢丝绳股径向结果对比

对于不同丝间接触类型产生的性能差异，图8给出了拉伸加载过程中交互捻和同向捻绳股各层钢丝间接触界面位置的最大von Mises应力与最大等效塑性应变演变情况。由图8(a)可知，两类绳股在芯丝-内层侧丝(CW-IW)接触部位具有相近的结果：应力均随拉伸应变的增加而线性增加，且均在应变达到0.006后发生应力屈服而产生塑性变形，随后因材料硬化而较屈服前应力增加速率有所减小，同时绳股发生屈服后等效塑性应变均随拉伸应变呈近似线性增加趋势。图8(b)则表明：两类绳股在内层侧丝-外层侧丝(IW-OW)接触区的应力应变演变规律存在一定异同，两类绳股应力均以“双线性”规律增加，但加载初期交互捻绳股应力增加率明显大于同向捻绳股，后者晚于前者发生应力屈服和塑性变形，以致前者的最终塑性应变约为后者的5倍。由上述可知，同向捻绳股在拉伸载荷工况下具有更好的抗屈服性及径向受载能力。

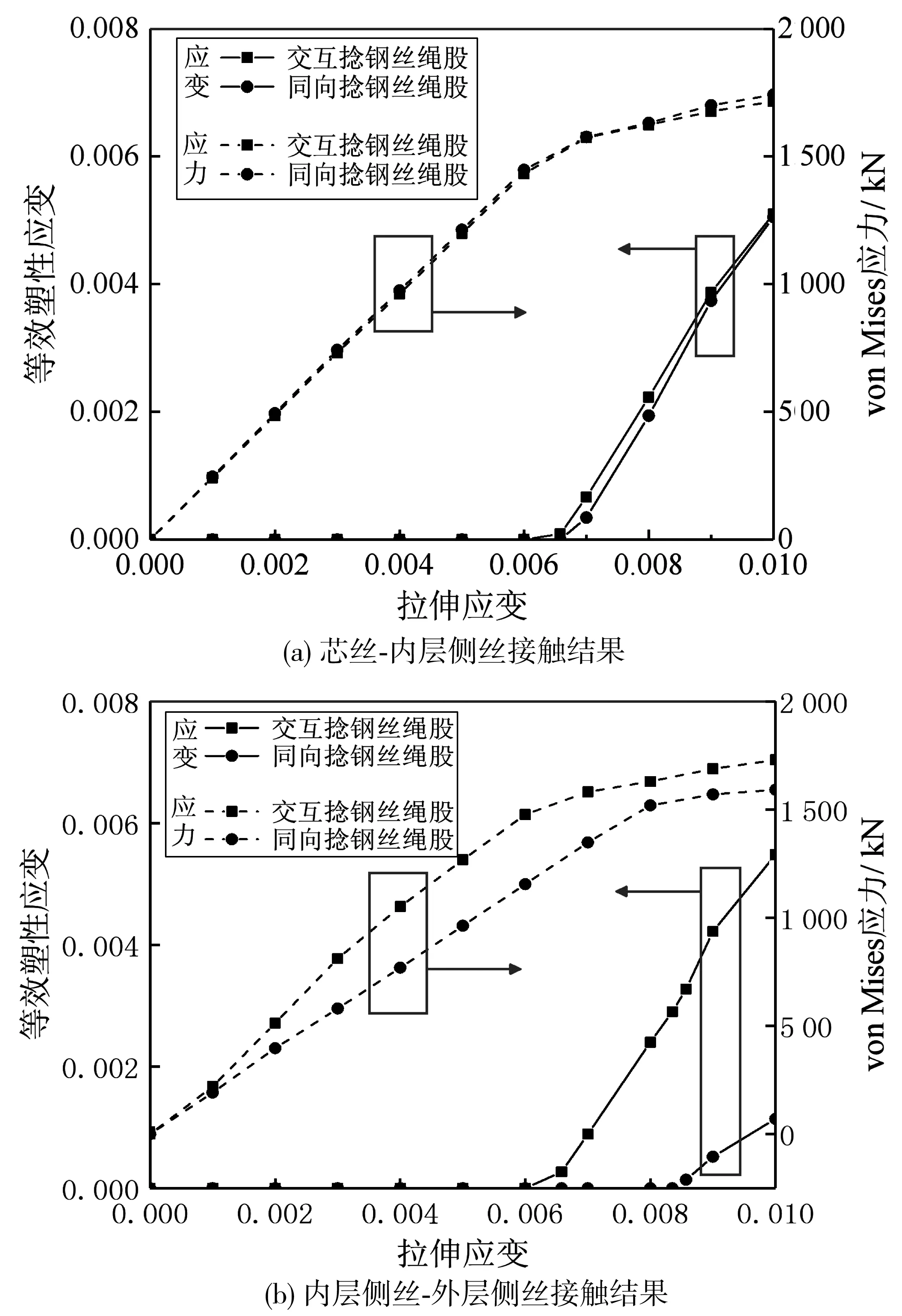
图8 交互捻和同向捻钢丝绳股不同接触区应力应变对比

图9为交互捻和同向捻绳股各层钢丝在轴向拉伸载荷下的承载分布。由图9可知，两类绳股各层钢丝具有相近的轴向力变化趋势，其中外层12根侧丝(OW)的轴向力最大，内层6根侧丝(IW)次之，芯丝(CW)轴向力最小。对于拉伸载荷引起的钢丝扭矩，两类绳股结果存在明显差异：交互捻绳股各层丝扭矩方向并不都相同，CW无扭矩作用，IW与右旋一致，而OW所受扭矩与左旋一致，整股所受扭矩方向与OW相同；同向捻绳股内外层侧丝具有相同的扭矩方向，且芯丝同样不受扭矩作用，IW扭矩大于OW，且交互捻绳股的总扭矩小于同向捻绳股，由此可知，前者抗旋转性能优于后者。由上述可知，捻向对拉伸载荷作用下钢丝绳股的轴向力影响较小，而对其扭矩影响显著，该发现与L.LIU等[11]的研究结论一致。

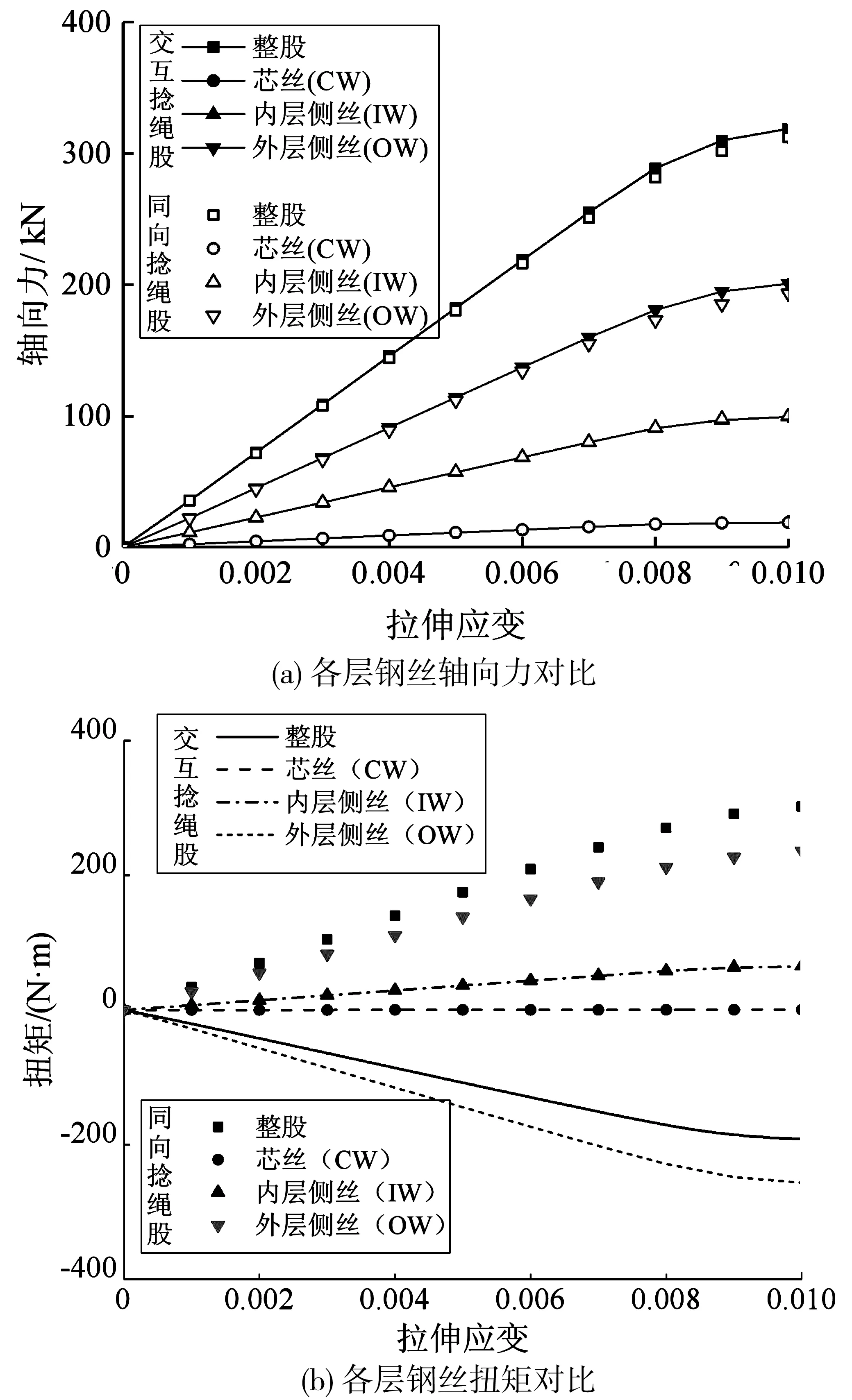
图9 交互捻和同向捻钢丝绳股各层钢丝承载分布对比

交互捻和同向捻多层结构钢丝绳股各层单根钢丝轴向力对比结果如图10。由图10可知，两类绳股各层单根钢丝的轴向力随拉伸应变的变化趋势相同，均表现为先近似线性增大，在达到应力屈服后增加速率逐渐减小。相同拉伸应变下，两类绳股各层单根钢丝的轴向力均表现为：芯丝(CW)最大，内层侧丝(IW)次之，外层侧丝(OW)最小，该结论与D.G.WANG等[9]所提及的结论相符，且二者在相同位置的单根钢丝所受的轴向力近似相同，由此可知，捻制方式对绳股单根钢丝轴向力影响较小。

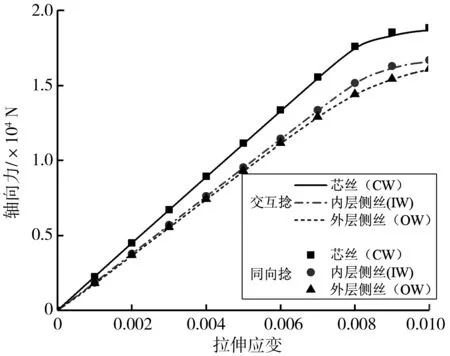
图10 交互捻和同向捻钢丝绳股各层单根钢丝轴向力对比

4 结 论

建立了交互捻和同向捻多层结构钢丝绳股的参数化几何模型，并考虑钢丝弹塑性、丝间摩擦和接触等因素，建立了上述两类钢丝绳股的有限元模型，对比分析了二者在轴向拉伸载荷作用下的服役性能差异，所得主要结论如下：

1)两类绳股在相同拉伸应变下具有相近的轴向力和von Mises应力，二者抗拉性能相当；相比于同向捻绳股，交互捻绳股产生了较小的扭矩，因而表现出较好的抗旋转性。

2)交互捻和同向捻绳股内层侧丝的应力应变沿绳股截面半径方向的变化明显不同，前者在芯丝-内层侧丝接触区达到峰值后减小，随之又增加，并在内层侧丝-外层侧丝达到最大值，而后者则沿径向一直减小。

3)拉伸过程中，交互捻绳股内层侧丝-外层侧丝接触处应力集中更明显，而同向捻绳股芯丝-内层侧丝接触处应力集中更突出；前者比后者更早发生塑性应变且最大塑性应变相差较大。

4)两类绳股的各层钢丝在拉伸过程中有近似相等的轴向力变化趋势；两类绳股芯丝均未产生扭矩，交互捻绳股内外层侧丝扭矩方向相反，整体扭矩与外层侧丝相同，都与左旋方向一致，同向捻绳股各侧丝及整股扭矩方向均与右旋方向一致，上述差异导致二者抗扭性能的不同。

5) 拉伸载荷下，捻制方式对多层结构钢丝绳股各层单根钢丝轴向拉力的影响较小，且各层单根钢丝轴向力由大到小为：芯丝最大，内层侧丝次之，外层侧丝最小。