基于正交试验法的风电场布局优化研究

陈丹丹

(上海电力设计院有限公司，上海 200025)

0 引言

对风电场进行布局时，优化风电机组的微观选址是非常重要的环节，其需要满足2个基本要求：1)最大限度地利用风电场的风能资源，提高发电量[1]；2)降低因地形或风电机组间相互干扰产生的尾流、湍流影响，并避开其他影响风电机组安全运行的因素，在提高发电量的同时提高风电机组运行的可靠性。

在对地形平坦的风电场进行布局时，往往是根据经验方法来布置风电机组，基本布置方法为：沿主风向布置时，风电机组之间的间距为5～9倍叶轮直径；沿与主风向垂直方向布置时，风电机组之间的间距为3～5倍叶轮直径，且风电机组尽量布置在风能资源较好的区域[2]。虽然这种经验布局很容易实现，但在主风向难以确定的情况下，这种布局往往难以达到风电场发电量和经济效益的最优。

目前，设计院在进行风电场微观选址时，通常是利用从国外引进的软件进行发电量和尾流损失模拟，比如：WAsP、WindFarmer、windPRO、WT等商业软件，但这些软件目前具有的优化功能并不能完全适应实际工程情况，需要进行人工干预。因此，有必要在总结现有风电场规划设计方法的基础上，进行新的风电场微观选址优化研究。基于此，本文提出一种新的不同于以往风电机组随机布置或规律排列的布局优化方式—— 基于正交试验法的风电场布局优化方法。该方法首先采用参数法先对整个风电场中的风电机组进行初始布置，然后利用正交试验法对风电机组位置寻优，考虑多种风资源条件后计算风电场全场尾流差，再重新调整风电机组位置，最后通过分析比较，选择出风电机组的最优位置，实现风电场的布局优化，完善了WAsP等软件的功能。

1 风电场的微观选址

本文提出的布局优化方法采用参数法对整个风电场中的风电机组进行初始布置，这种方法可以从整体上对风电场进行布局，符合大多数风电场的布局要求。

假设风电场是一个理想化的迎着主导风向的矩阵，且主导风向为西风，如图1所示，其中，α为排列角，为风电机组纵向排列时与风电场主导风向的夹角。该风电场的长度是指风电场与主导风向相同的方向上两端顶点之间的距离，比如AB、DC；在该长度下，共有p列风电机组，从左往右依次为1，2，…，p。风电场的宽度是指风电场与主导风向垂直方向上两端点之间的距离，比如AD、BC；在该宽度下，共有q行风电机组，从上往下依次为1，2，…，q。

图1 风电场矩阵图Fig.1 Wind farm matrix diagram

排列角、行间距比m、列间距比n为影响风电场布局的3个主要参数。行间距比可表示为：

式中：Da为第a行与第a+1行风电机组之间的间距，其中a＜q；Da+1为第a+1行与第a+2行风电机组之间的间距。

列间距比可表示为[3]：

式中：Lb为第b列与第b+1列风电机组之间的间距，其中b＜p；Lb+1为第b+1列与第b+2列风电机组之间的间距。

2 风电场发电量计算

2.1 风速分布计算

风能是一种具有波动性和随机性的能量，其大小受各种因素的影响。正是由于这种随机性的存在，对风能利用产生了较大的不利影响，限制了风电在新能源领域的发展。随着数理统计学科的发展，风速的分布并不是完全无迹可寻，目前风速分布可以通过风速概率分布函数来表示。

经过各方验证，威布尔分布曲线最具有代表性，因此，风电行业最常采用威布尔分布作为风速概率分布函数。威布尔分布曲线主要通过形状参数和尺度参数来描述，且这2个参数的取值不能为负数。

2.2 尾流损失计算

尾流是影响风电场发电量的重要因素。平坦地形下的尾流计算较为简单，无需考虑地形高程导致的入流角产生的影响，本文中的尾流计算使用较为简单的Jensen模型和Lissaman模型。

Jensen模型示意图如图2所示，其中：R为风电机组叶轮的半径；Rw为尾流的影响半径；v0、vT、vX分别为来流风速、经过叶轮的风速和受尾流影响后的风速[4]；假设风电场中某风电机组所在点位x=0，则与其相邻的另一台风电机组所在点位x=X。

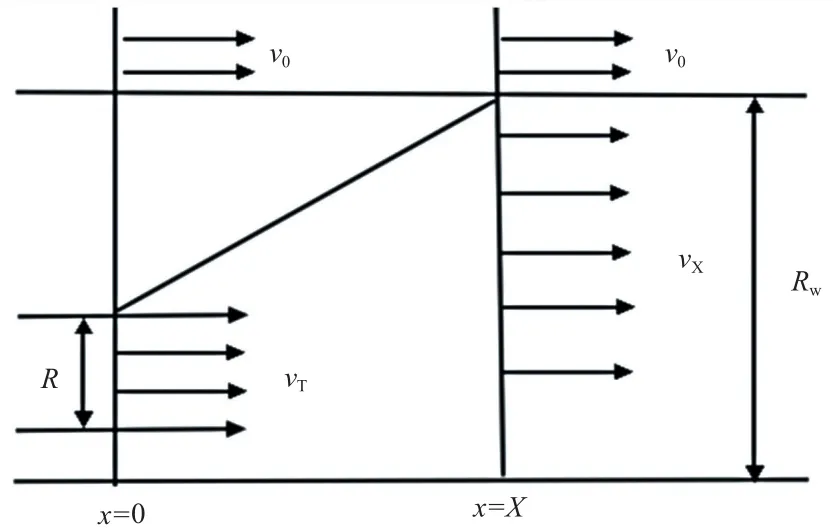
图2 Jensen 模型示意图Fig.2 Schematic diagram of Jensen model

来流风速、经过叶轮的风速和风电机组的推力系数CT之间的关系可表示为：

则有：

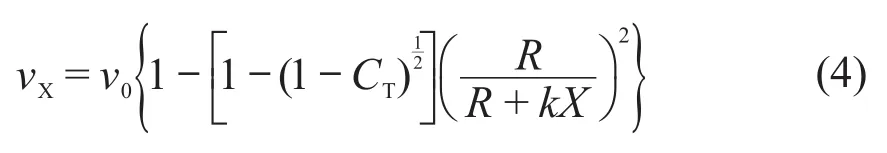
式中：k为尾流耗散系数。

不同情况下的尾流耗散系数可从表1中选取。

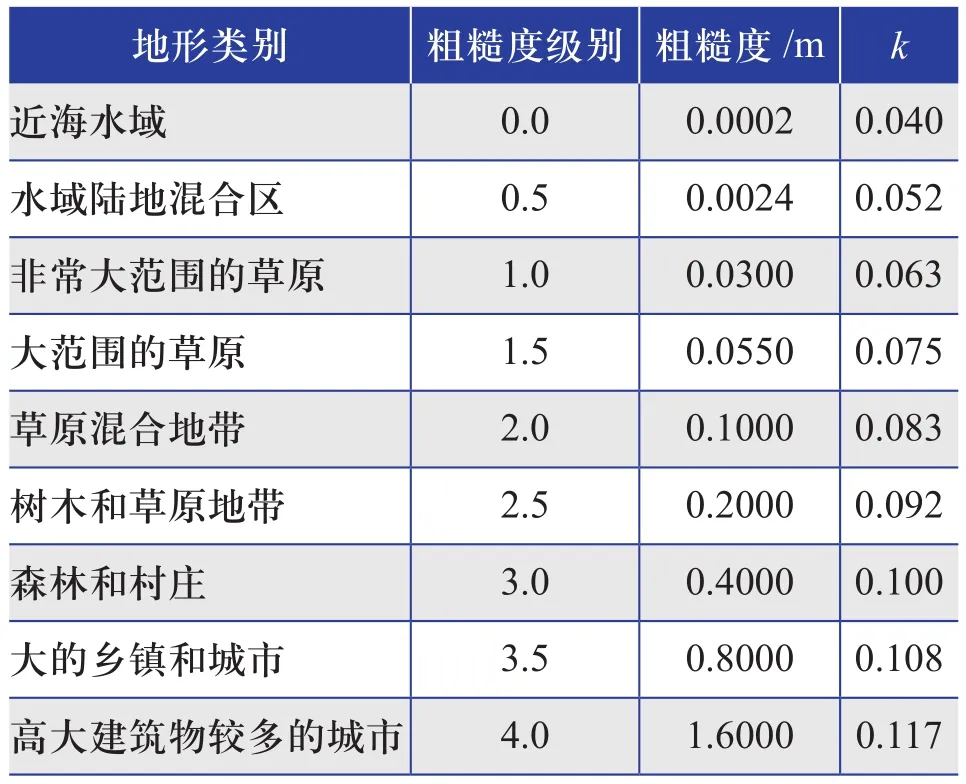
表1 不同情况下的尾流耗散系数Table 1 Wake dissipation coefficients in different cases

Lissaman模型除了可用于高度相同的风电机组，还可用于风电机组有高度差的情况，其示意图如图3所示。其中：h为风电机组的轮毂高度；z0为海平面高度；z(i)为第i台风电机组所在地的海拔高度；z(j)为与第i台风电机组相邻的第j台风电机组所在地的海拔高度。

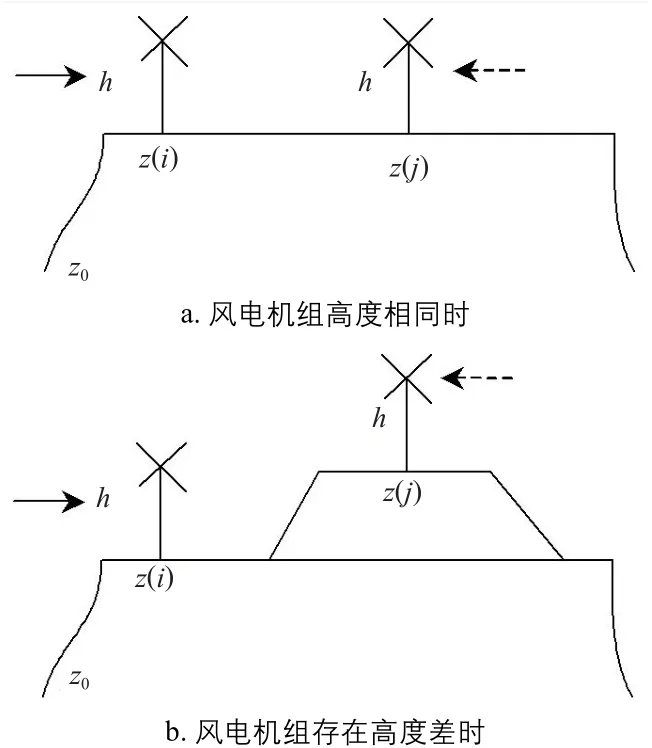
图3 2 种情况下的 Lissaman 模型Fig.3 Lissaman model in two cases

根据风切变原理，位于海拔高度H处的风电机组接收到的风速v′0为：

式中：α1为风速随高度变化系数。

假设在x=0处有1台风电机组，则x=X处的风电机组必然会受到来自上风向风电机组的影响，根据贝努利方程可得到图3b中z(j)下的风电机组的风速v2x，其可表示为：

式中：α′为风剪切系数。

根据动量守恒定律，并结合上述的尾流模型，可以得到经过尾流影响后第j台风电机组在t时刻的风速vj(t)，其可表示为：

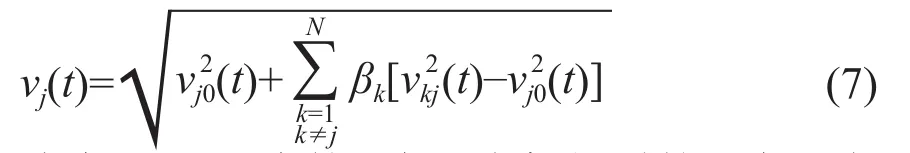
式中：vkj(t)为第j台风电机组受第k台风电机组尾流影响后的风速；vj0(t)为第j台风电机组未受到尾流影响时的风速；N为风电机组的总台数；βk为第k台风电机组在第j台风电机组位置上的投影面积Ashad-jk与第j台风电机组叶轮扫风面积Arot-j的比值[5]。

2.3 发电量计算

第j台风电机组的发电量Ej可表示为：

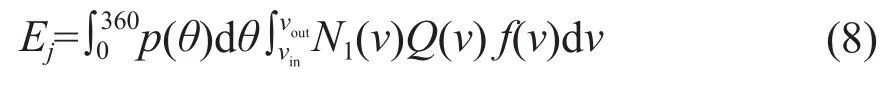
式中：p(θ)为风向角度为θ时的风向频率；vin为风电机组的切入风速；vout为风电机组的切出风速；N1(v)为相应风速等级的全年累计小时数；Q(v)为风速v时通过功率曲线得到的风电机组功率；f(v)为通过威布尔分布曲线得到的风速v的频率。

整个风电场的发电量E可以看成是所有风电机组发电量的代数和，其可表示为：

3 风电场微观选址的优化设计

3.1 风电场理想矩阵向实际矩阵的转化

假设存在一个理想的由风电机组构成的风电场矩阵，即风电场的区域足够大，使所有风电机组都在风电场的边界内，而且整个风电场区域中不存在不可用区域，即所谓的“敏感地带”，比如：自然保护区、旅游景区、军事设施、文物、矿产等，风电机组可布置在风电场内的任意区域。本文研究的风电机组布置不同于一般的矩阵排布、梅花形排布，而是采用两端紧凑中间稀疏的布置，假设主导风向为西风，通过MATLAB软件编程可实现在风电场矩阵内理想的风电机组布置方式，如图4所示。图中：横轴代表风电场所在地形图的横坐标，纵轴代表风电场所在地形图的纵坐标；单位均为m。

图4 理想的风电场矩阵图Fig.4 Ideal wind farm matrix diagram

图4是理想的风电场矩阵，但在实际风电场中，风电机组排列时会有很多限制条件[6]，因此需要将该理想矩阵转换成一个实际矩阵，转换规则如下：

1)矩阵转换过程中依附于主导风向，即风电场矩阵的长边与主导风向保持平行，但允许有一定的角度偏转。由于实际风电场是有边界的，当软件生成的风电场矩阵“越出边界”时，需要屏蔽掉越出边界的风电机组。

2)在实际的风电场中，可能会遇到敏感地带，矩阵转换过程中会自动读取风电场敏感地带的数据，并在进行风电场矩阵偏转处理等步骤中屏蔽掉这些敏感地带，从而生成一个实际的风电场矩阵，具体如图5所示。图中：横轴代表风电场所在地形图的横坐标，纵轴代表风电场所在地形图的纵坐标；单位均为106m。

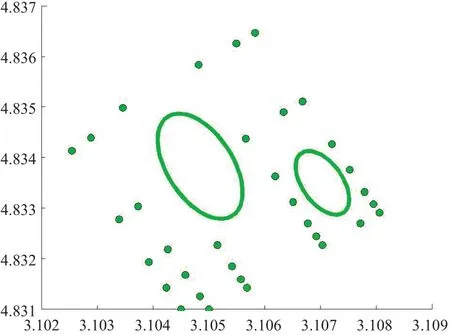
图5 实际的风电场矩阵图Fig.5 Actual wind farm matrix diagram

图5中圈出的区域表示的是由于风电场敏感地带而自动屏蔽的点，在这些区域内的风电机组已被算法自动屏蔽。对于该风电场矩阵，主导风向为西南风，因此将平行于主导风向排列的风电机组定义为行，垂直于主导风向排列的风电机组定义为列。

3.2 风电场布局参数的正交试验法

对于排列角、行间距比、列间距比这3个影响风电场发电量的因素，排列角的取值范围为-45°～45°，行间距比的取值范围为0.5～1.0，列间距比的取值范围为1.0～1.5。本试验分别从这3个因素中取3个值，通过采用“三因子三水平”试验条件设计，共可得到27种试验条件；根据得到的不同试验条件下的风电场发电量结果，对这3个因素进行直观分析，分别得出每个因素不同水平时对风电场发电量的影响程度，由此可以得出单个因素水平最优时的组合方式。

通过进一步地交互分析，分析2个因素组合时的效果，这是因为可能会存在“单个因素的水平最优，整体并不是最优，但2个因素的2个水平组合效果更好”的情况。然后根据此时得出的风电场发电量对排列角、行间距比、列间距比这3个因素分别进行两两分析，得出其影响程度，并和直观分析出的结果进行比较。

由于各个因素对于风电场发电量结果都会有影响，因此根据以上的分析结果，只能得出对应于1个因素的不同水平的先后影响顺序，但通过方差分析则可得出各个因素在各水平下的影响程度。综合上述过程则可以确定对于发电量影响最显著的各因素的水平组合(α，m，n)就是优化后的最终结果，即在这3个因素的水平最优取值组合下可得到风电场发电量最优的结果。

3.3 风电场布局的梅花形排布

通过对影响风电场布局的3个因素的正交试验法，可以得到初始优化后的风电场布局方式，此时的风电场布局有待于进一步优化，借鉴了工程上常用到的梅花形排布方案，该方案对风电场矩阵中风电机组的行、列进行隔行错位排布，然后将风电场发电量最高时的排布形式作为最优方案。

优化前的梅花形排布方案如图6所示。图中：横轴代表风电场所在地形图的横坐标，纵轴代表风电场所在地形图的纵坐标，单位均为106m；色条代表风电场所在地形图的海拔高度，单位为m。

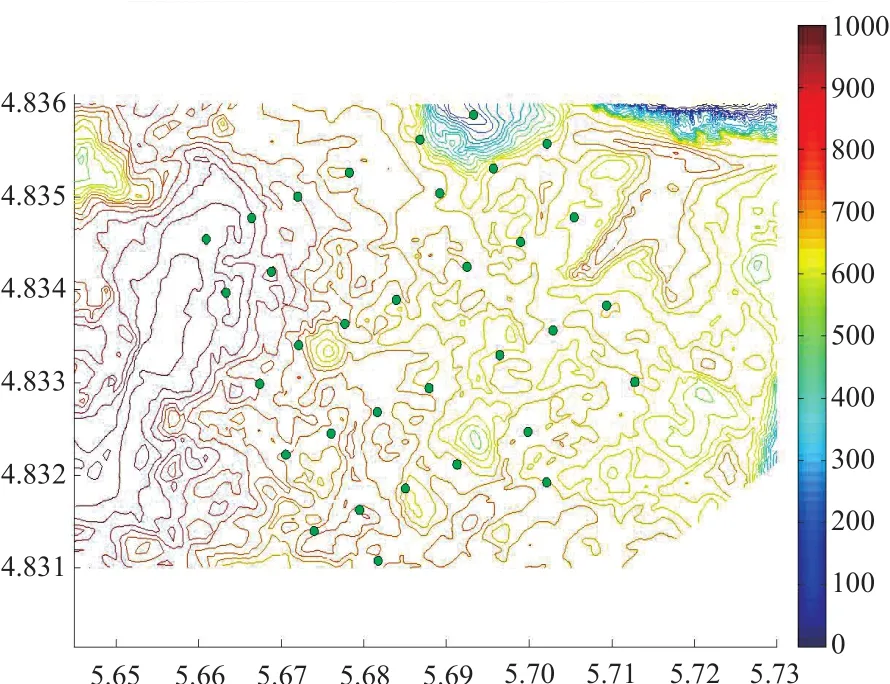
图6 梅花形排布方案优化前Fig.6 Before optimization of plum blossom layout scheme

对图6中的梅花形排布方案进行优化，具体的优化规则为：从风电场矩阵的第2行开始进行错位移动，移动的步数是4倍的风电机组间距，即每行风电机组的移动步数为4；每移动一次都要记录该移动所对应的风电场发电量及尾流损失，在该行移动完成后锁定最优的移动方案，并在此基础上进行隔行的错位移动。梅花形排布方案优化后如图7所示。图中：横轴代表风电场所在地形图的横坐标，纵轴代表风电场所在地形图的纵坐标，单位均为106m；色条代表风电场所在地形图的海拔高度，单位为m。

图7 梅花形排布方案优化后Fig.7 After optimization of plum blossom layout scheme

3.4 风电场布局沿主风向优化移动

根据风电场设计人员的经验，在风电场内部，尾流分布是不均匀的[7]，尾流沿着主风向越来越大，因此可以通过调整前后排风电机组的间距来调节尾流的分布，使尾流逐渐向上风向的风电机组靠近，促使整个风电场的尾流分布均匀，从而能够对风电场做进一步优化。

风电场布局沿主风向优化移动的步骤为：首先找到尾流损失最大的风电机组所在的列，需要移动的列从第2列开始至该列。第1列保持不动，第2列向第1列移动，第3列向第2列移动，移动精度根据需要设置，每移动一步都要记录此时风电场发电量与每台风电机组的尾流值；该列移动完成后，保留最优移动，并在此基础上进行下一列的移动。在移动过程中要满足风电机组的最小间距条件、尾流限制条件及风电场边界条件，同时还要避开敏感地带。风电场布局沿主风向的优化移动演示如图8所示。图中：横轴代表风电场所在地形图的横坐标，纵轴代表风电场所在地形图的纵坐标，单位均为106m；色条代表风电场所在地形图的海拔高度，单位为m。

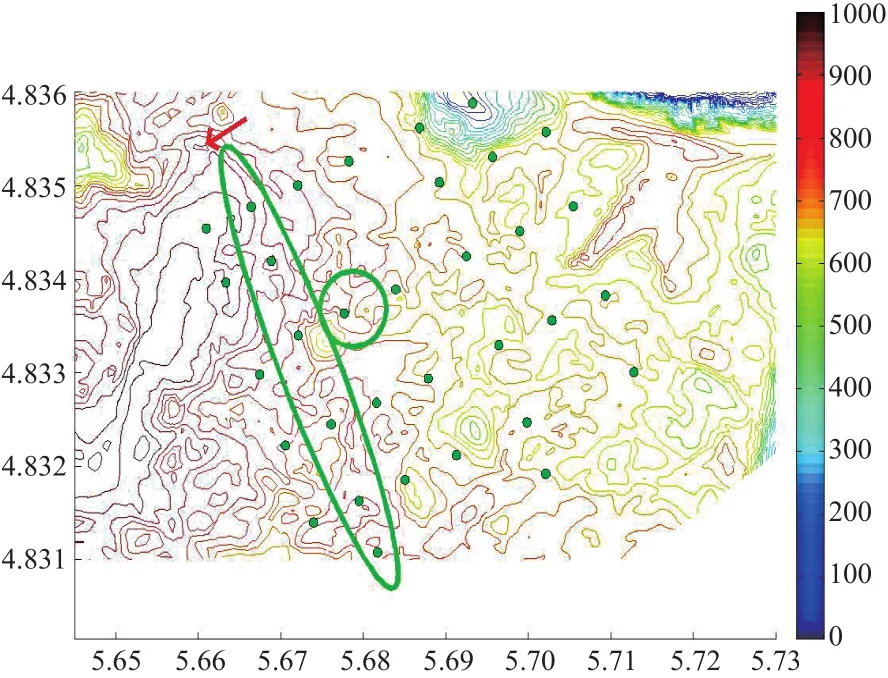
图8 风电场布局沿主风向的优化移动演示图Fig.8 Demonstration diagram of optimized movement of wind farm layout along the main wind direction

根据风电场设计人员的丰富经验，在对风电场布局沿主风向优化移动的基础上，还可以对垂直主风向上的风电机组进行优化移动，以作为前者的补充，使整个风电场呈现“中间紧凑，两边稀疏”的布局。

风电场布局沿垂直主风向的优化步骤为：首先找到尾流最大的风电机组所在的行，发生优化移动的行为距离矩阵中心最近的一行至该行，且剩下的行同时发生对称移动。移动规则与风电场布局沿主风向优化移动规则一致。风电场沿垂直主风向的优化移动演示如图9所示。图中：横轴代表风电场所在地形图的横坐标，纵轴代表风电场所在地形图的纵坐标，单位均为106m；色条代表风电场所在地形图的海拔高度，单位为m。

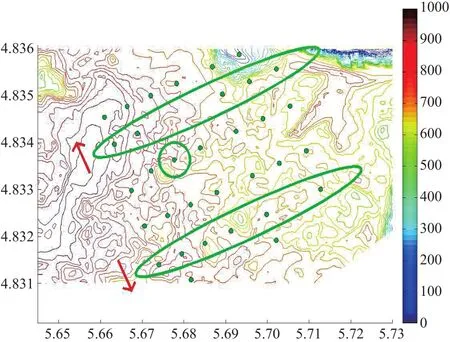
图9 风电场布局沿垂直主风向的优化移动演示图Fig.9 Demonstration diagram of optimized movement of wind farm layout along vertical main wind direction

4 风电场发电量计算结果分析

基于上文采用正交试验法对风电场布局的优化分析，以某实际风电场为例，对该风电场进行布局与发电量模拟。

4.1 风电场描述

此处选用图6所示的风电场地形图和布置方式进行分析。该风电场海拔高度范围在954～975 m之间，地形高差不大，地势平缓，可以假设为平坦地形；该风电场包括33台单机容量为1.5 MW的风电机组。

在MATLAB软件程序里导入地形图(.map)、风资源文件(.tab)、风电机组位置文件(.txt)、风电机组功率曲线与推力曲线(.wtg)等信息，然后在考虑地表粗糙度、障碍物影响的基础上，选择风速范围及优化过程的步长，并选择距离罚则作为限定条件。设定距离罚则有助于评估整个风电场设计时的基础设施的造价。风电场设定好后，距离风电场最远的风电机组将获得相应的罚则值，从而调整成一个较为紧凑的风电场布局，以减少电缆(海缆)用量。

4.2 风电场微观选址优化结果

风电场微观选址的优化结果为风电场年发电量达198.59 GWh，除去尾流影响后的净发电量达206.71 GWh，风电场全场平均尾流损失达3.93%。该算法程序结合了正交试验法，完善了WAsP等风电场微观选址时发电量计算软件的功能，优化后的风电机组布置如图10所示。图中：横轴代表风电场所在地形图的横坐标，纵轴代表风电场所在地形图的纵坐标，单位均为106m；色条代表风电场所在地形图的海拔高度，单位为m。

从图10中可以发现，风电机组排布呈现不完整的梅花形排布，这是因为避开了一些敏感地带和尾流损失较大的位置。

图10 优化后的风电机组布置Fig.10 Optimized wind turbine layout

4.3 比较分析

利用WAsP软件计算得到：采用经验布置方法(即优化前)时该风电场年发电量为195.202 GWh，该值比优化后最终得到的风电场年发电量198.59 GWh少1.71%左右；优化前的尾流损失达到4.50%，比优化后最终得到的3.93%高出了12.67%。造成这些差异的主要原因是经验布置方法未考虑尾流因素的优化。

5 结论

针对以往风电机组随机布置或规律排列的布局方式，本文提出一种基于正交试验法的风电场布局优化方法，得到以下结论：

1)本文提出的风电场布局优化方法是以参数法为基础，采用正交试验法，对各种步长的调整并进行计算来优化风电机组布置的方案。由于设置了边界作为约束条件，故不会增加布置区域面积，换言之，在相同布置面积下相较于常规的等行列距方法可以减少尾流损失，提高发电量，且易实施。

2)采用本文提出的优化方案得到的发电量计算结果与采用WAsP软件得到的经验布置方式下的计算结果比较接近，符合微观选址工作的要求；并且优化过程中的自主排布功能和优化功能也是WAsP软件所不具备的，因此该方法可以很好的应用于风电场微观选址的前期工作中。