面向无人集群的通信定位一体化方法研究
胡晨骏,辜方林,赵 林,赵 莺,魏急波
(1. 国防科技大学电子科学学院, 长沙 410073;2. 北京信息通信技术研究中心,北京 100036)
0 引言
无人集群在协同作战中,相互之间除了信息传输必不可少之外,还得获取位置、速度等空间状态信息,即传输信息和测距定位都是无人集群实现协同工作的重要基础。而传统的通信和定位系统往往采用独立的硬件平台,使用不同的信号波形、调制方式和信号功率,占用不同的频率和带宽,难以实现无人平台通信与测量设备的集约化设计。鉴于通信链路进行信息共享是无人平台之间协作的基础,无线电定位以其独特的优势已然成为实现平台之间相对定位的一种自然手段。如果通信和定位波形在载波频率、射频天线、波形设计、调制方式和信号处理等方面进行统一设计,实现通信、定位系统深层次的一体化融合,则能够极大降低网络系统资源占用及信号处理复杂度,减少频谱占用和能量消耗。综上所述,研究无人协同系统的通信和定位一体化具有十分重要的意义。
美国国家航空航天局(National Aeronautics and Space Administration,NASA)的空间通信和导航(Sp-ace Communication and Navigation,SCaN)计划是近几年美国关于空间通信与导航定位系统研究的重要项目,聚焦于通导一体化波形设计、导航(测距测向)方法和组网协议等,值得我们借鉴。中国区域定位系统(Chinese Area Positioning System,CAPS)具备高精度定位授时和短报文的收发功能,且已在实际应用中发挥了巨大作用。约翰霍普金斯大学的应用物理实验室(Applied Physics Laboratory’s,APL)构建了集成通信和导航的功能的APL系统,其核心是利用时分多址(Time Division Multiple Access,TDMA)循环测距的方法实现相对导航定位,但是由于TDMA系统时延较大,难以满足实际需要。冯奇从通信和导航的基本性能指标出发,提出了基于V-OFDM调制的通信和导航一体化系统;北京邮电大学邓中亮教授等提出了时分码分正交频分复用(Time & Code Division-Orthogonal Frequency Division Multiplexing, TC-OFDM)信号体制,其核心是通过对通信信号资源的复用,实现高精度的室内外定位。但是,OFDM信号体制的信号峰均比高、对频偏敏感且抗干扰能力弱,难以适用于军事行动、无人集群等面临的复杂、动态的应用环境。
准确测量节点之间的距离是实现网络中节点间相对定位的必要条件。根据无线电测距原理,距离测量值等于信号到达时间与信号发送时间之差和光速的乘积,信号发送时间可以通过时间戳来标定,信道到达时间则需要通过精准到达时刻的测量获得。在准确到达时间测量的基础上,发展出了到达时间(Time of Arrival,TOA)定位方法和到达时间差(Time Difference of Arrival,TDOA)定位方法等。可以看出,精准到达时间测量问题解决的好坏直接影响定位精度,因此,无线电定位系统的核心技术之一就是实现高精度无线电信号到达时间测量。直接序列扩频(Direct Sequence Spread Spectrum,DSSS)系统由于频谱展宽需要高的采样频率,对应的采样间隔的时间分辨率高,同时用于扩频的伪随机(Pseudorandom Noise,PN)码具有良好的相关特性,通过计算接收信号与本地PN码的互相关发现,接收信号与本地PN码完全对齐时互相关出现尖锐峰值,其余情况互相关值很小,因此,检测其峰值即可获得具有极高时间分辨率的同步性能。另一方面,DSSS系统具有较强的抗窄带干扰能力,并且具有信息隐蔽、多址保密等优点,适用于军事行动等复杂应用场景。然而,目前DSSS技术局限于低速通信系统或者信道环境简单、干净的卫星通信系统,为了满足无人系统面临的多径环境下通信和相对定位一体化的需求,一方面需要引入均衡技术克服多径导致的频率选择性衰落,实现高效可靠通信;另一方面,通信定位一体化波形必须解决信号到达时间的高精度测量问题,现有方法一般是在实现定时同步(码片同步)的基础上,通过Costas环等环路鉴相或者训练序列进行载波相位估计实现精同步,从而满足定位、授时的需求。
本文提出了一种单载波频域均衡(Single Carrier Frequency Domain Equalization,SCFDE)与DSSS技术有机结合的通信定位一体化波形。一方面,SCFDE系统具有与OFDM类似的实现框架,OFDM的许多性质在SCFDE系统中同样适用。例如,利用频域均衡克服多径导致的频率选择性衰落、基于频域载波相位的高精度时间同步等,且相较于OFDM,SCFDE具有对频偏不敏感、易于与DSSS结合、峰均比较低等优点,能适用于高动态、电磁环境复杂等恶劣环境。另一方面,利用优选的恒包络零自相关(Constant Amplitude Zero Auto Correlation,CAZAC)序列作为信道估计的导频序列,根据CAZAC序列的傅里叶保持性质,将SCFDE系统中导频序列通过傅里叶变换(Fast Fourier Transform,FFT)变换到频域,并与本地导频符号进行循环移位相关,检测相关峰值即可实现整数符号周期信号到达时间估计。在此基础上,结合用于信道估计的导频序列,构建差分延时相关模型,实现载波相位估计,解决小数采样周期信号到达时间估计问题,最终实现高精度的信号到达时间估计,使系统同时满足定位授时的应用需求。
1 基于SCFDE的DSSS通信抗干扰波形
本文提出了一种基于SCFDE的DSSS通信抗干扰波形,其系统框架如图1所示。该波形的核心思想是采用DSSS体制获得抗干扰能力,同时引入频域均衡克服信道频率选择性衰落的影响,实现高可靠通信。
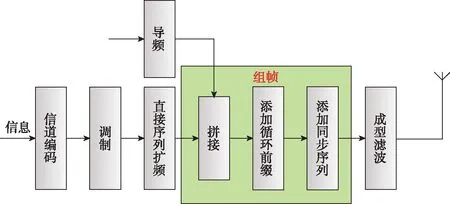
(a) 发送端

(b) 接收端图1 基于SCFDE的DSSS通信定位一体化波形框架Fig.1 DSSS communication positioning integrated waveform framework based on SCFDE
发送端由信道编码、调制、DSSS、组帧和成型滤波等单元组成,信息比特首先经过信道编码、调制等模块形成信息符号,再经过DSSS单元形成高速信息符号,此后将用于信道估计的导频符号与信息符号按照特定规律进行拼接,并添加循环前缀(Cyclic Prefix,CP)和同步符号完成组帧,最终经过成型滤波生成发射信号。接收端由匹配滤波、时频同步、解帧、信道估计与均衡、逆傅里叶变换(Inver-se Fast Fourier Transform,IFFT)、解扩及判决等单元组成,接收信号完成A/D转换后经过匹配滤波实现带外干扰抑制,而后经过时频同步模块实现伪码同步、定时同步和载波频差估计与补偿,在此基础上完成帧解析,并将信号通过FFT变换到频域,并利用导频符号完成信道估计与均衡,再将信息符号通过IFFT转化为时域信号,完成解扩、信道译码等后续处理。
特别指出,导频符号与信息符号的处理方式不同,信息符号经过扩频、解扩处理以保证高的接收机灵敏度和好的抗干扰等通信能力指标,而导频符号则不进行扩频处理,便于实现DSSS带宽扩展后高的时间分辨率,提升时间同步精度,进而提升定位精度。假设CP的长度大于信道的冲激响应长度,则导频用于频域信道估计的过程可以表示为
=·+
(1)
其中,=FFT()表示接收的导频符号对应的频域值;=FFT()表示导频符号的频域值;=FFT()表示信道响应的频域值;=FFT()表示噪声的频域值;符号“·”表示2个向量的点乘。可以看出,若导频符号的频域信号幅值恒定,则信道估计不需要除法,只需要乘法就可以实现,可以大大减少实现复杂度。另一方面,为了使发送信号的峰均比小,需要导频符号的时域信号幅值恒定。综合上述分析,本文提出了导频信号采用CAZAC序列,CAZAC序列有两个优良特性:一是序列具有良好的自相关特性和互相关特性,即该序列互相关值很小几乎为零,而自相关值较大,在做相关运算时能够表现出优异的峰值特性;二是幅值恒定,且CAZAC序列经过FFT和IFFT后仍为CAZAC序列,所以同时使用了FFT和IFFT运算的系统不会对该序列的性质产生影响。
2 面向定位的高精度信号到达时间估计方法
无线电定位的核心是实现高精度的信号到达时间测量。事实上,无线通信系统的核心和难点之一也是通过时频同步模块实现收、发端之间的时间和频率校准,但是它对信号达到时间测量的精度要求没有定位系统那么高。例如,对于SCFDE、OFDM等插入CP进行码间串扰保护的系统,只需达到小于CP保护间隔的时间同步精度要求。然而,无线电定位系统则对信号到达时间的检测精度要求十分严苛,即使达到信号采样周期这样的精度也远远不够。例如,假设采样率为10MHz,理论上得出的信号到达时间差最小为100ns,换算成距离则是30m,而这样的精度是没有办法接受的。
针对上述问题,结合基于SCFDE的DSSS通信抗干扰波形,本文提出了一种如图2所示的高精度到达时间估计实现框架。为了提升信号到达时间的估计精度,利用优选的CAZAC序列作为信道估计的导频序列。导频序列通过FFT变换到频域,并与本地导频符号进行循环移位相关,检测相关峰值即可实现整数符号周期信号到达时间估计。在此基础上,结合用于信道估计的导频序列,构建差分延时相关模型,实现载波相位估计,解决小数周期信号到达时间估计问题,最终实现高精度的信号到达时间估计,使系统同时满足测距和定位的应用需求。

图2 高精度信号到达时间估计框架Fig.2 Precision arrival time estimation framework
2.1 整数采样周期信号到达时间估计
通过插入CP进行保护,只要时频同步模块引入的定时误差(以符号周期为单位)小于CP长度,定时误差对时域和频域接收信号的影响如表1所示。

表1 定时误差的影响
另一方面,假设{()}是一个长度为(为偶数)的CAZAC序列,则()可表示为
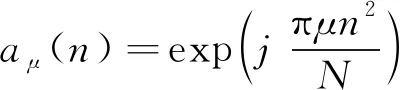
(2)
其中,∈[0,-1];是与互质的正整数。可以证明,CAZAC序列具有恒模、傅里叶保持、良好的自相关和互相关特性,这些性质对于信道估计和高精度时间同步具有重要意义。
CAZAC序列通过FFT变换后仍然为CAZAC序列,可以表示为

(3)
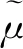
CAZAC具有良好的自相关和互相关特性,CAZAC序列的相关性可表示为

(4)
其中,表示时刻偏差;表示序列周期。可以看出,它具有理想的周期自相关性质,即当序列完全对齐时,则存在尖锐的峰值,当序列存在偏差未对齐时,则相关值接近于0。因此,利用该性质可实现高精度的定时估计。如图3所示,通过计算导频序列接收信号的频域响应与本地频域导频序列之间的互相关,检测其相关峰值即可实现准确的整数符号周期的估计。

图3 基于本地互相关的整数符号周期时间估计Fig.3 Arrival time estimation of integer symbol period based on local cross correlation
2.2 小数采样周期信号到达时间估计
利用导频序列本地互相关模块估计得到的整数采样周期信号到达时间对接收信号进行时间校正,时间校准后频域导频信号可以表示为
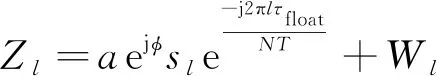
(5)
式中,表示第个子载波上的加性高斯白噪声。由于已知,假定某一子载波数量间隔为,且是正整数,越小,能够估计的定时偏差范围越大,反之,亦然。利用导频序列本地互相关模块能够获得准确的整数采样周期估计,因此,小数采样周期信号到达时间重点解决1个符号周期偏差范围内的精确估计即可,因此,取值为2。令

(6)
结合式(5)和式(6),可得
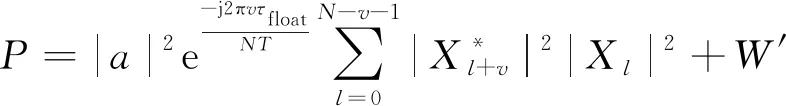
(7)
式中,′是噪声项。的相位为
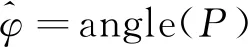
(8)
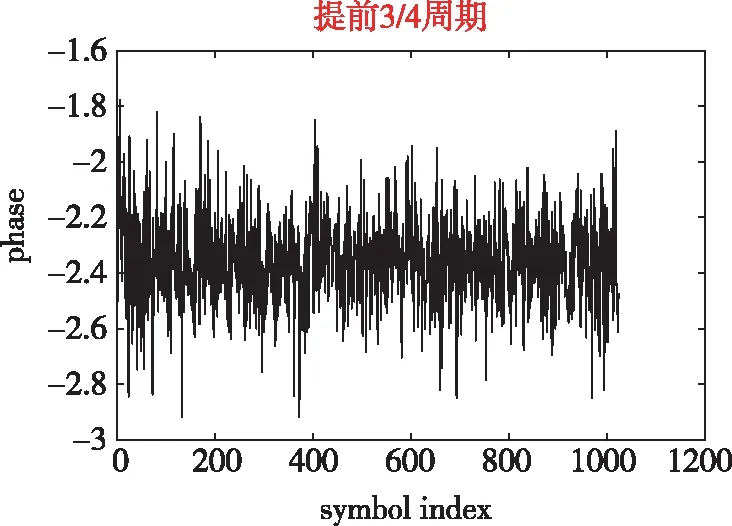
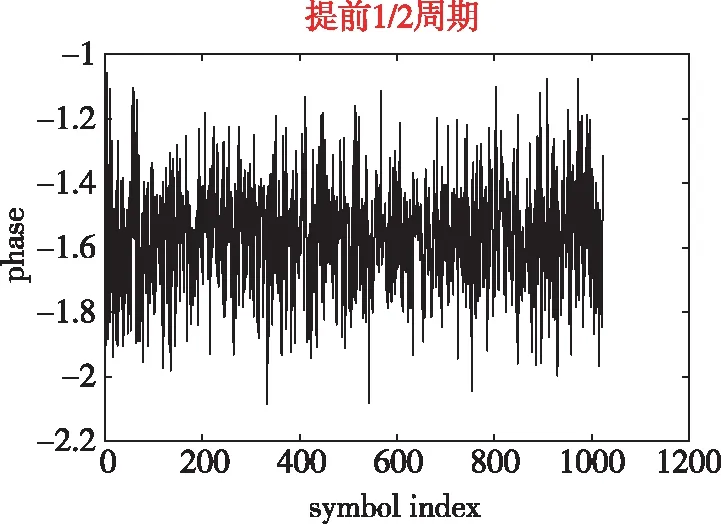
式中,angle(·)表示取相位运算。如图4所示,每幅子图为式(6)、式(7)中0,1,…,--1个采样点展现出来的相位样值。通过计算这些相位的平均值可以看出,没有时延时,其相位平均值约为0;1/4符号时延偏差时,其相位平均值约为0.78(π/4);1/2符号时延偏差时,其相位平均值约为1.57(π/2);3/4符号时延偏差时,其相位平均值约为2.35(3π/4)。因此,式(8)计算求解的相位与分数符号周期时延之间存在一一对应关系。因此,SCFDE信号的信号达到时间频域估计为

(9)


(10)
(a)
(b)

(c)

(d)图4 基于延时差分的小数符号周期时间估计Fig.4 Arrival time estimation of decimal symbol period based on differential delay correlation
3 仿真分析
3.1 基于SCFDE的DSSS系统的通信性能
随着扩频倍数的增加,系统能否稳定获得扩频增益的改善是衡量所提方案用于构建通信链路的有效性的一个重要指标。因此,对基于SCFDE的宽带DSSS系统在各种信道环境下进行误码率仿真分析。首先,仿真分析了基于SCFDE的宽带DSSS系统在高斯白噪声信道环境下的误码性能。
图5给出了系统误码性能随接收信号信噪比变化的曲线,可以看出,随着扩频倍数的增加,系统的误码性能有明显改善,且扩频倍数每增加1倍,接收性能改善约2dB。

图5 高斯白噪声信道条件下误码性能随接收信号信噪比的变化曲线Fig.5 Curves of BER with SNR under AWGN channel
其次,仿真分析了基于SCFDE的宽带DSSS系统在典型多径信道环境下的误码性能。
图6给出了本文所提基于SCFDE的宽带DSSS系统不同扩频倍数下误码性能随接收信号信噪比变化的曲线。可以看出,随着扩频倍数的增加,系统的误码性能稳步改善,且扩频倍数每增加1倍,接收性能改善约1.6dB。因此,基于SCFDE的宽带DSSS系统能够适应复杂多径环境,实现可靠通信。

图6 多径信道条件下误码性能随接收信号信噪比的变化曲线Fig.6 Curves of BER with SNR under multi-path channel
3.2 基于SCFDE的DSSS系统的信号到达时间估计精度
信号到达时间估计精度是影响无线电定位系统的核心,因此,本文对基于SCFDE的宽带DSSS系统在各种信道环境下信号到达时间估计精度进行仿真分析,评估实现无线定位的可行性。具体仿真参数如表2所示。

表2 系统仿真参数
仿真分析了基于SCFDE的宽带DSSS系统在高斯白噪声和多径信道环境下的小数采样周期信号到达时间的估计精度。整数采样周期信号到达时间估计和小数采样周期信号到达时间估计模块是同时工作的,且需要这两个模块相互配合才能实现高精度的信号到达时间估计。由于CAZAC具有良好的相关特性,可以准确完成整数采样周期信号到达时间估计和补偿,此时理想的小数采样周期信号到达时间应该为零。但是由于噪声、多径等因素的影响,导致估计的小数采样周期信号到达时间存在误差,本文将该误差作为评估小数采样周期信号到达时间估计精度的依据。
图7给出了本文所提基于SCFDE的宽带DSSS系统小数采样周期信号到达时间估计精度随接收信号信噪比的变化曲线。可以看出,其估计误差会随着系统信噪比的恶化而增大。高斯白噪声信道条件下,估计误差随信噪比增大而线性降低;多径环境下,估计误差随信噪比变化存在平层。但是,无论是高斯白噪声信道还是多径信道,在系统接收信号信噪比不低于0dB的条件下,小数采样周期信号到达时间的估计误差不会大于0.3个采样时刻,显著提升了信号到达时间的估计精度,满足定位授时所需的高精度时间同步要求。

图7 小数采样周期到达时间估计精度随接收信号信噪比的变化曲线Fig.7 Curves of arrival time estimation accuracy of decimal sampling period with SNR
4 结论
本文提出了一种SCFDE与DSSS技术有机结合的通信定位一体化波形,在具有较高速率、抗窄带干扰通信能力的同时,利用CAZAC序列优良的自相关和互相关特性,将其作为导频序列并计算导频序列与本地导频符号的循环移位相关,检测相关峰值即可实现整数符号周期信号到达时间估计。特别地,结合用于信道估计的导频序列,构建差分延时相关模型,实现载波相位估计,完成小数采样周期信号到达时间估计,从而实现高精度的信号到达时间估计。

