基于因子图的状态估计方法运算实时性研究
孙 涛,郑 辛,常 琦,吴亮华
(1.北京自动化控制设备研究所, 北京 100074;2.中国航天科工集团有限公司, 北京 100048;3.火箭军装备部装备项目管理中心, 北京 100089)
0 引言
目前,国内主流的研究因子图算法的方式是通过开源库GTSAM(Georgia Tech Smoothing and Mapping),根据确定好的因子图模型,定义并添加需要的因子节点,利用库中实现的因子图算法来解决状态估计问题。文献[1]中针对水面无人艇导航系统确定了惯性/卫星/多普勒计程仪组合导航的因子图模型,建立了惯性传感器(Inertial Measurement Unit,IMU)、全球卫星导航系统(Global Navigation Satellite Syst-em,GNSS)、多普勒计程仪(Doppler Velocity Log,DVL)的因子节点,并研究了观测值异常的处理方法;文献[2]中针对船用导航系统确定了惯性/北斗/多普勒计程仪/天文组合导航的因子图模型、建立了IMU、北斗卫星导航系统(BeiDou Navigation Satellite System,BDS)、DVL、天文导航系统(Celestial Naviga-tion System,CNS)的因子节点,并研究了传感器的故障检测方法;文献[3]中针对陆用车载导航系统确定了惯性/卫星/里程计组合导航的因子图模型、建立了惯性导航系统(Inertial Navigation System,INS)、GNSS、里程计(Odometer,OD)的因子节点,并验证了其处理传感器异步和时延的性能。
但与确定因子图模型和定义因子节点相比,因子图算法才是GTSAM的核心。因子图算法有消元算法、增量平滑与地图构建(Incremental Smoothing and Mapping,iSAM)算法、iSAM2 (Incremental Smoothing and Mapping using the Bayes tree)算法。其中iSAM算法和iSAM2算法是一种通用的增量推断算法,适用于任意的因子图模型,但算法复杂且不易实现。利用因子图算法去分析具体的因子图模型,并获得适用于该因子图模型的增量推断算法是另一种研究方式。
本文基于第二种研究方式,梳理了因子图算法及其理论基础之间的关系,使用消元算法分析了一元观测因子图模型的稀疏结构,得到了一种适用于该因子图模型的增量推断算法,并验证了该增量推断算法在求解一元观测因子图模型的状态估计问题时运算速度的提升能力;同时,研究了固定滞后平滑算法,实现了滑窗在该增量推断算法中的应用,并验证了滑窗维持运算速度稳定的能力。
1 理论基础
图1中梳理了因子图算法及其理论基础之间的关系,标*表示不常用。

图1 因子图算法及其理论基础Fig.1 Factor graph algorithm and its theoretical basis
因子图算法的理论基础是非线性优化。根据贝叶斯公式,并在输入和观测是相互独立,状态和观测符合多维高斯分布的假设下,对状态进行最大后验估计等价于求解非线性最小二乘问题。
求解非线性最小二乘问题的方式有解析方式和迭代方式,而迭代方式将求解非线性最小二乘问题转化为获取使目标函数值下降的修正量的问题,其中获取修正量的方法有梯度下降法、牛顿法、高斯牛顿法、列文伯格-马夸尔特法及Dogleg法等。
求解高斯牛顿方程的方式可分为全局推断、稀疏推断及增量推断。全局推断,直接对高斯牛顿方程进行求解,方法有直接求逆法、QR分解法、Cholesky分解法;稀疏推断,利用稀疏结构进行求解,方法有稀疏QR分解法、稀疏Cholesky分解法、消元算法等;增量推断,无需重新分解并利用前上三角矩阵,仅更新受新因子影响的部分,方法有iSAM算法、iSAM2算法。
1.1 最大后验估计
根据贝叶斯公式,并且在给定、的情况下,有
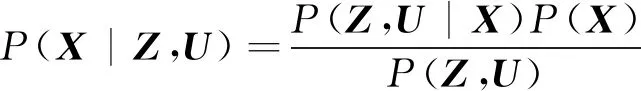
(1)
即后验概率密度正比于观测概率密度(,|)与先验概率密度()的乘积,其中,={,,…,}为所有状态;={,,…,}为所有观测;={,,…,}为所有输入。
所有输入和观测是相互独立的,对观测概率密度进行因式分解

(2)

各状态和观测符合多维高斯分布,已知多维高斯分布~(,∑),∈×1的概率密度函数表示为
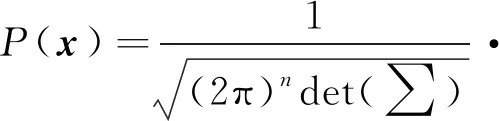
(3)
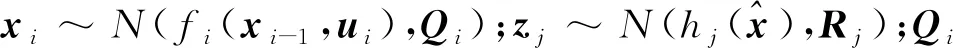
对所有状态进行最大后验估计可表示为
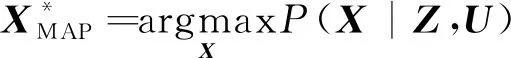
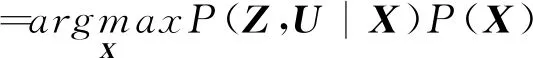
(4)
对(,|)()取负对数,因为对数函数单调递增,所以对(,|)()求最大化等价于对(,|)()的负对数求最小化。

(5)
在上述假设下,并忽略常数项及系数可得


(6)
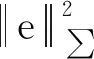
将马氏范数转化为2-范数,即
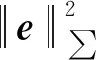
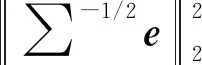
(7)
将式(7)代入式(6)中,可得

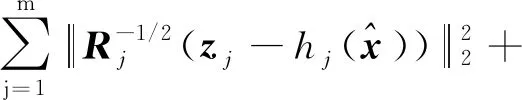

(8)
对状态进行最大后验估计等价于求解使目标函数值达到最小值的所有状态的问题。当(·)或(·)是非线性函数时,该问题为非线性最小二乘问题;当(·)和(·)均是线性函数时,该问题为线性最小二乘问题,求解非线性最小二乘问题的方法也适用于线性最小二乘问题。
1.2 求解方式及方法
如果目标函数的数学形式简单,则可以用解析方式直接求解,即令目标函数的导数为零,然后求解得到导数为零处的极值点,最后代入目标函数,逐个比较它们的函数值大小即可。
在导函数的数学形式复杂,且随着目标函数中状态个数不断增加的情况下,极值点求解困难且个数会呈几何倍增长。目前,求解非线性最小二乘问题,通常采用迭代的方式:从一个初始值出发,求解使目标函数值下降的修正量,并修正所有的状态。大致的求解流程如下:
1)给定初始值={,,…,,0};
2)在第次迭代,获取使目标函数值下降的修正量
Δ={Δ0,,1,,…,,}
3)若Δ足够小或使目标函数值上升,则停止迭代;
4)否则,令+1=+Δ,返回第2)步。
其中,表示第次迭代时的所有状态;,表示第次迭代时的状态;Δ,表示第次迭代获得的的修正量。
因此,迭代方式中获取使目标函数值下降的修正量是关键,方法有梯度下降法、牛顿法、高斯牛顿法、列文伯格-马夸尔特法以及Dogleg最小化法。本文主要开展基于高斯牛顿法的推断算法研究。
第次迭代时,高斯牛顿法获取的修正量公式为
()()Δ=-()()
(9)
式(9)被称为增量方程或高斯牛顿方程。
2 消元算法及固定滞后平滑算法
2.1 消元算法
在文献[7]中,马尔可夫随机场与海森矩阵相对应,而马尔可夫随机场可体现出海森矩阵的稀疏结构。在因子图算法中,因子图与雅可比矩阵相对应,且因子图可体现出雅可比矩阵的稀疏结构;贝叶斯网络与上三角矩阵相对应,且贝叶斯网络可体现上三角矩阵的稀疏结构。
消元算法是一种将因子图转化为因子化的贝叶斯网络的算法,实质上是将稀疏雅可比矩阵分解为上三角矩阵的算法。但与稀疏QR分解和稀疏Cholesky分解相比,消元算法是一种更加通用的稀疏矩阵分解法,它适用于任何能够表示为因子图的稀疏矩阵。
算法实现流程如下:
1)选定消元顺序;
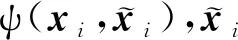
3)重复步骤2),直至将因子图完全转化为因子化的贝叶斯网络


(10)

2.2 固定滞后平滑算法
非线性优化是一种批量估计方法,需求解所有状态的修正量Δ。因此,随着状态个数的不断增加,运算速度会变慢,需通过滑窗限制状态量个数,维持运算速度稳定。固定滞后平滑算法为实现滑窗提供了理论指导。
固定滞后平滑算法是在添加一个状态后,对除了最近个状态的其他状态进行边缘化,仅需修正最近的个状态的算法,类似于滑动窗口操作。
结合消元算法,固定滞后平滑算法的实现步骤如下:
1)使用消元算法,将(迷你)因子图转化为因子化的贝叶斯网络;
2)在因子化的贝叶斯网络上,对除了最近个状态的其他状态进行边缘化;
3)加入新状态后,将因子化的贝叶斯网络中与新状态相连的状态转化回因子图,与新状态相连的因子节点一起构成迷你因子图后,返回步骤1)。
固定滞后平滑算法是对因子化的贝叶斯网络中的状态进行边缘化。简单地将因子图中除最近个状态的其他状态及相连的因子节点丢掉绝不等价于边缘化,这会导致信息的丢失。
3 一元观测因子的因子图模型
3.1 稀疏结构分析
一元观测因子的因子图模型是除了状态转移因子外,观测因子均为一元的因子图模型,而一元观测因子并非仅有一种观测因子,而是指仅与一个状态相关的观测因子。典型的一元观测因子图模型有速度、位置或姿态匹配的因子图模型。
如表1所示,一元观测因子的因子图模型在增加新的一元观测因子后,使用消元算法得到的因子化贝叶斯网络与之前的因子化贝叶斯网络结构相同,即对应的上三角矩阵具有相同的稀疏结构;而增加新状态后,因子化的贝叶斯网络所对应的上三角矩阵的稀疏结构仍具有一定的规律性:在对角线、状态与其下一个状态的对应处具有非零矩阵块,其余均为零矩阵块,并且仅最新状态与其上一个状态的对角线及对应处非零矩阵块发生变化,标_表示发生变化。
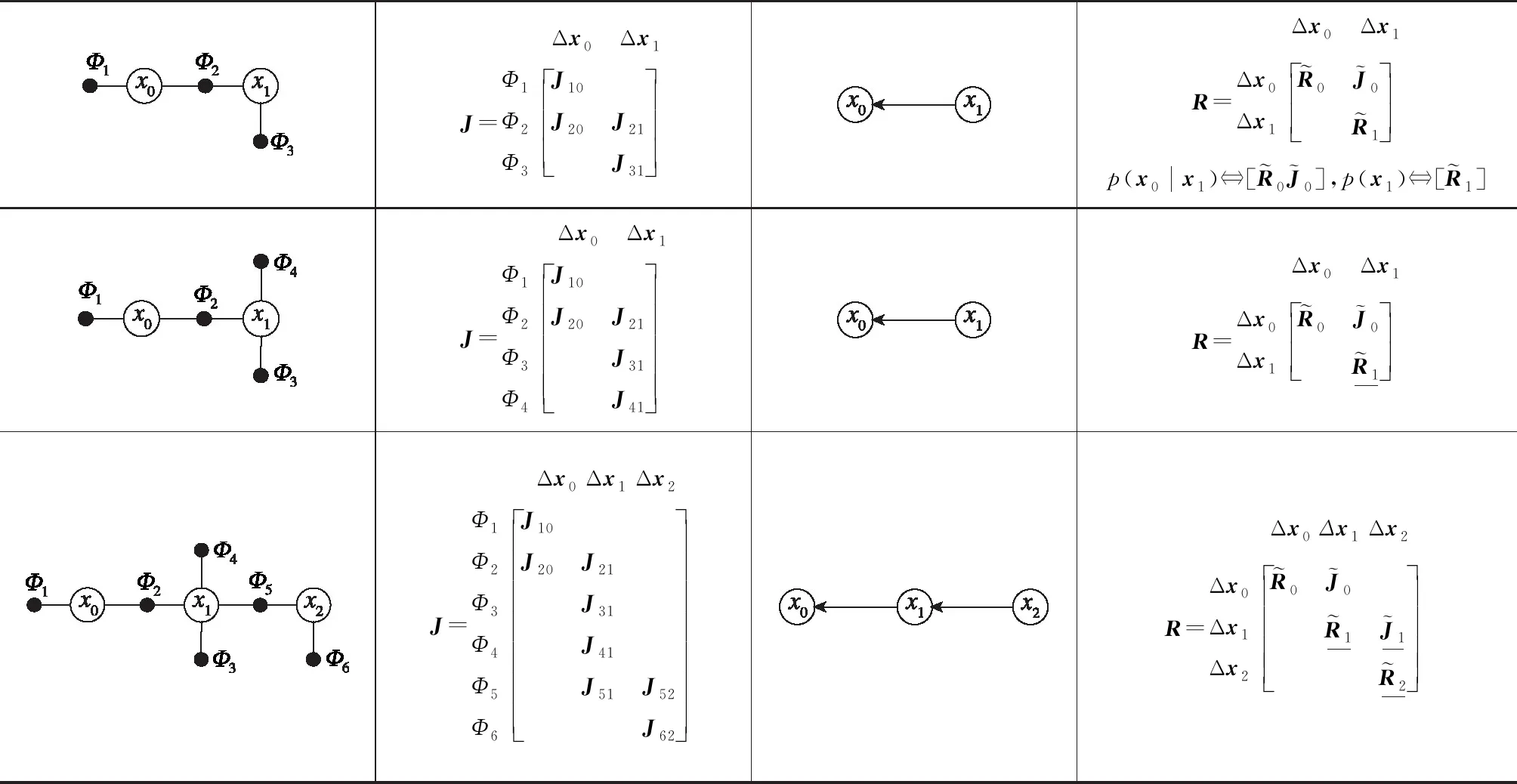
表1 一元观测因子的因子图模型
3.2 增量推断算法
已知=,由3.1节的规律性及增量推断思想,提出了一种适用于一元观测因子图模型的增量推断算法,伪代码如下:
()
{
(==1)
{
//(-1)是与-1相连的因子对应的非零矩阵块
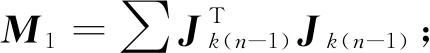
}
{


}



//()是与相连的因子对应的非零矩阵块

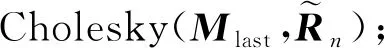
}
(11)
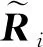

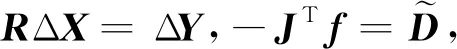
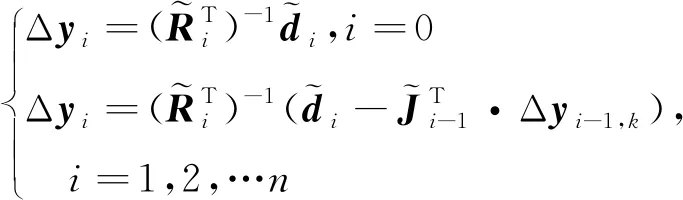
(12)
再通过反向替代求解Δ=Δ得到修正量Δ。
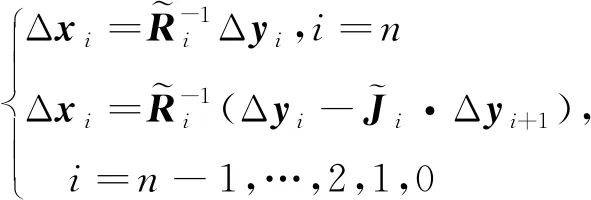
(13)
3.3 滑窗实现
根据固定滞后平滑算法,滑窗需要在因子化的贝叶斯网络上进行,但是为了求解Δ=Δ=-获得修正量Δ,还需要获得滑窗后的因子图。
滑窗后的因子图如图2所示,将因子图中滑窗之外的其他状态及相连的因子节点丢掉后,需要对滑窗中第1个状态添加一个先验因子。加入先验因子后的滑窗因子图转化为因子化贝叶斯网络,与滑窗后的因子化贝叶斯网络相等即可。该实现方法可实现任意的滑窗方式,“窗口为,进1出1”、“窗口为,进”等。
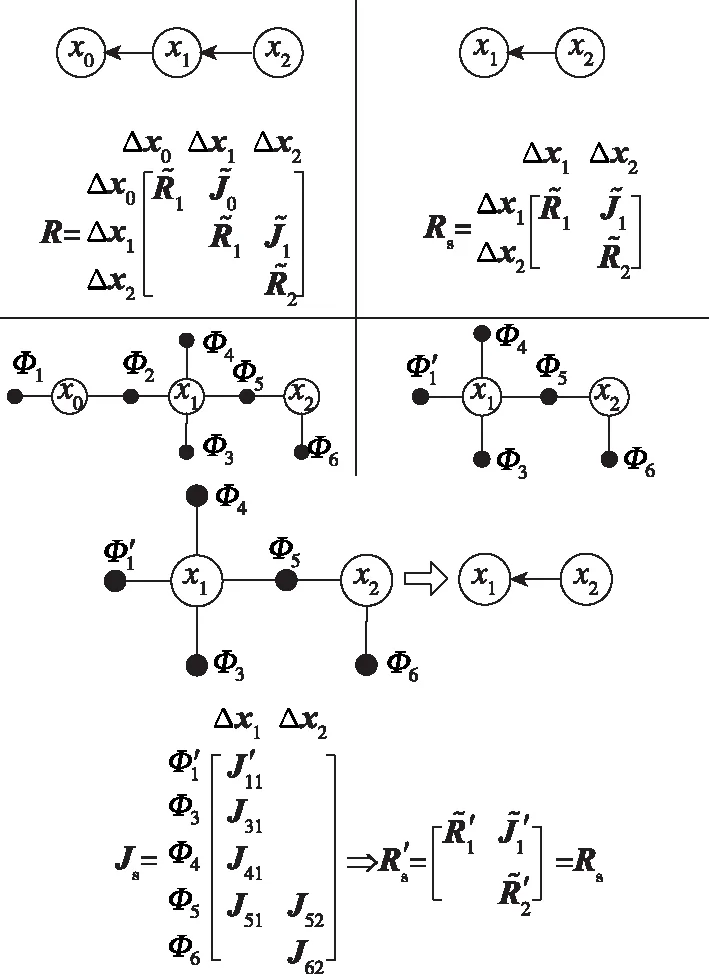
图2 滑窗后因子化贝叶斯网络及因子图Fig.2 Factorized Bayesian networks and factor graphs after sliding window
4 仿真验证与分析
速度匹配的因子图模型就是典型的一元观测因子图模型。如图3所示,除状态转移因子、、外,观测因子、、仅与一个状态相关。因此,本文以15维惯导误差作为状态量,使用静基座条件下两位置速度匹配,验证基于因子图的状态估计方法的估计能力、该增量推断算法对运算速度的提升能力及滑窗维持运算速度稳定的能力。
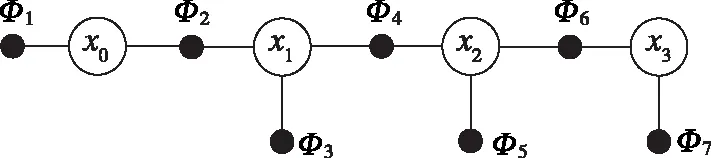
图3 速度匹配的因子图模型Fig.3 Factor graph model for velocity matching
4.1 建立模型
系统模型如下

(14)
状态量为15维惯导误差
=[δδδδδδ

]

状态转移因子为

(15)
其中,=·,为两个状态量之间的时间间隔。
观测因子为

(16)

采用输出校正的方式,当接收到零速观测时,添加新状态并确定相应的状态转移因子及观测因子,否则一直更新状态转移因子。
4.2 仿真验证

如图4所示,绘制了真实状态曲线,增量推断、滑窗增量推断的估计曲线及增量推断、滑窗增量推断与真值的绝对偏差曲线,其中后两个算法仅存储对最新状态的估计值。
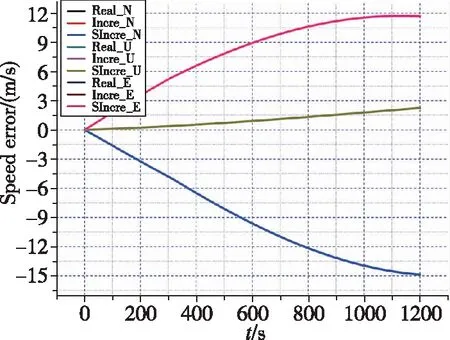
(a) 速度误差
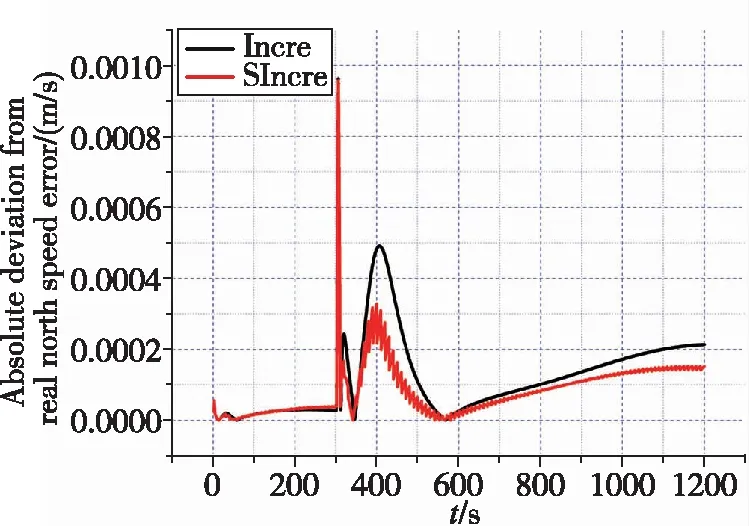
(b) 北速误差绝对偏差
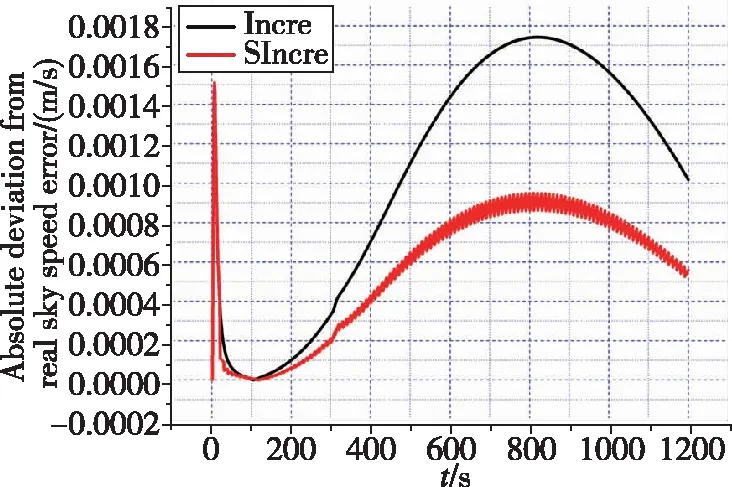
(c) 天速误差绝对偏差

(d) 东速误差绝对偏差

(e) 位置误差
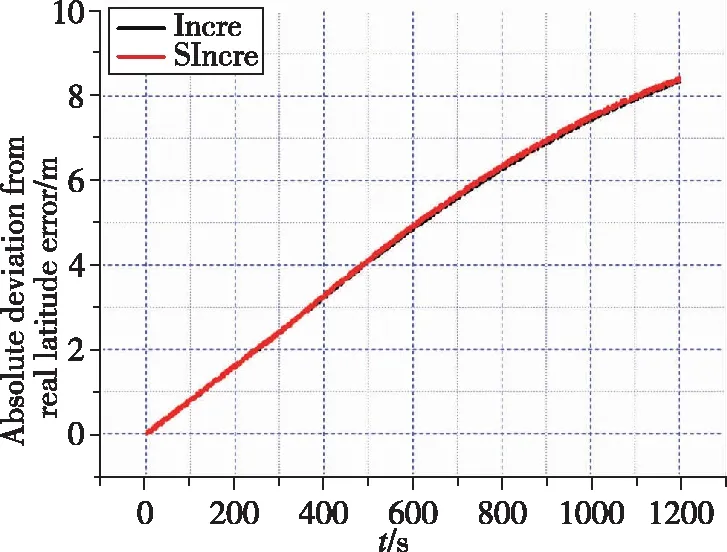
(f) 纬度误差绝对偏差
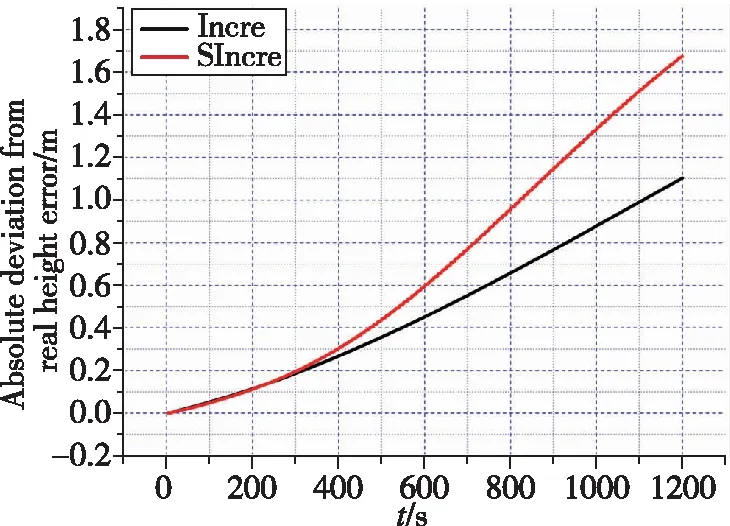
(g) 高度误差绝对偏差

(h) 经度误差绝对偏差

(i) 失准角

(j) 北向失准角绝对偏差

(k) 天向失准角绝对偏差

(l) 东向失准角绝对偏差
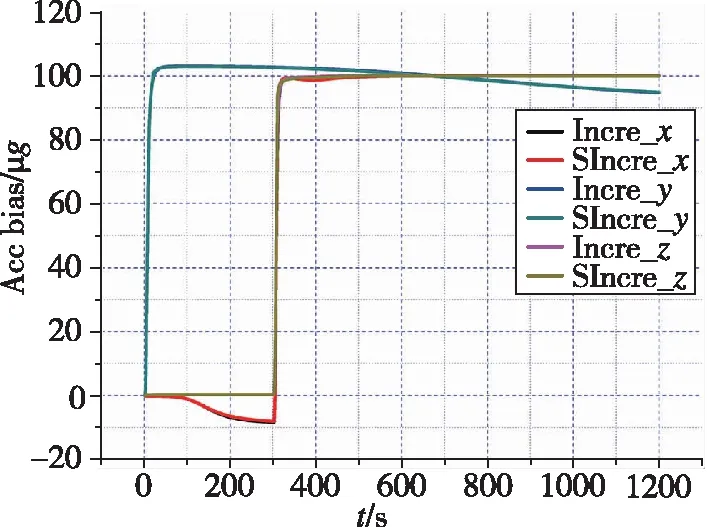
(m) 加表零位

(n) X向加表零位绝对偏差
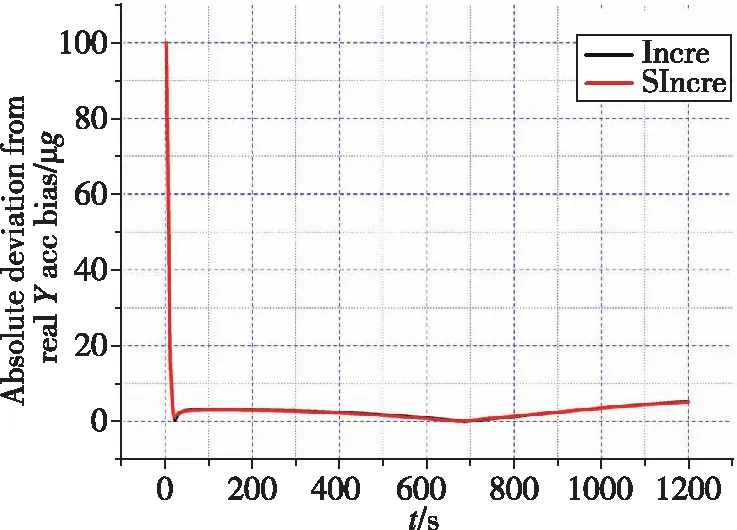
(o) Y向加表零位绝对偏差

(p) Z向加表零位绝对偏差
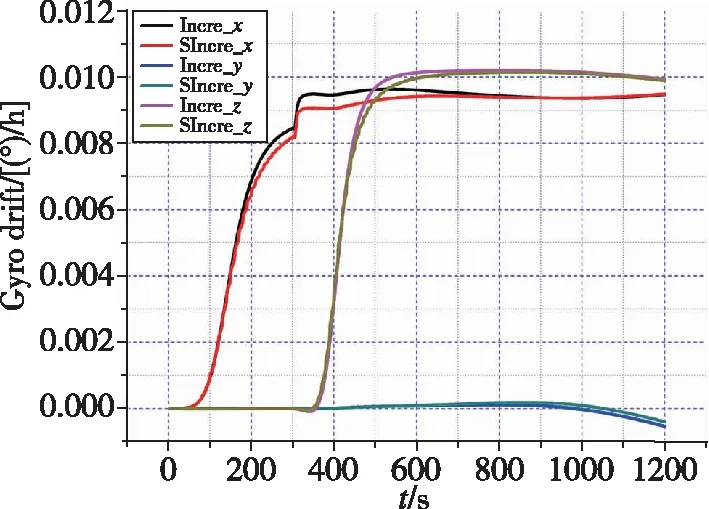
(q) 陀螺漂移
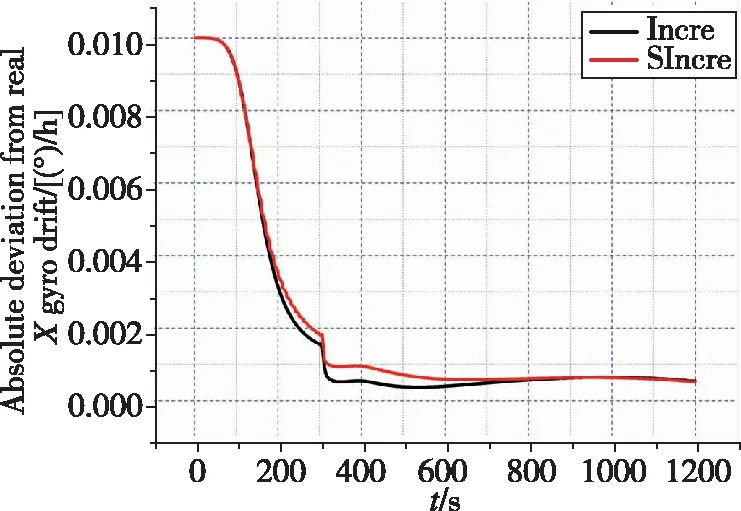
(r) X向陀螺漂移绝对偏差
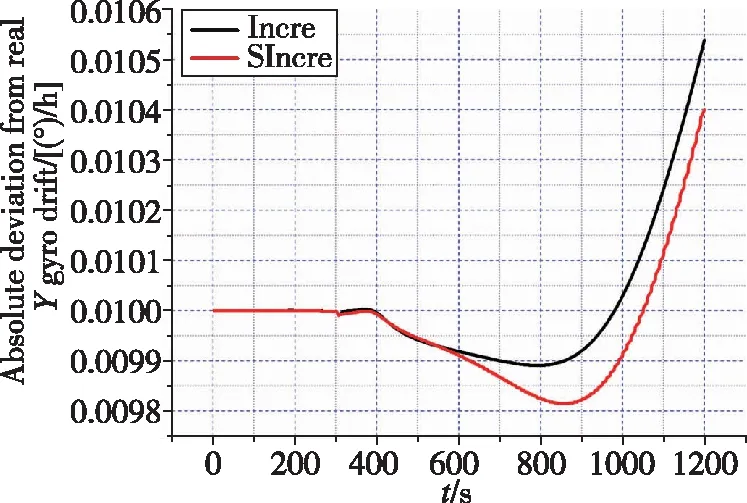
(s) Y向陀螺漂移绝对偏差
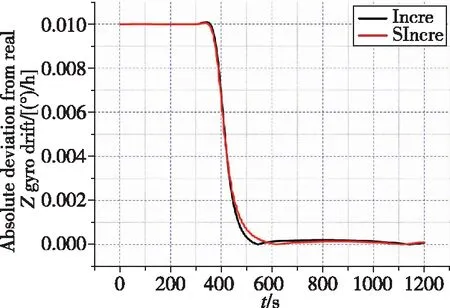
(t) Z向陀螺漂移绝对偏差
如图4和表2所示,与真实状态相比,基于因子图的状态估计方法的速度误差绝对偏差的量级在10m/s;位置误差在最终时刻偏差最大,最大偏差与真实状态之比为8.33m/-10582.6m、1.10m/1176.6m、12.89m/9441.4m,量级均在10以下;最终时刻北向、天向、东向失准角与真实失准角的偏差为(9.69×10)°、(2.38×10)°、(1.55×10)°;除向陀螺漂移,其他惯性器件误差与真实值偏差逐渐减小,从而验证了基于因子图的状态估计方法的状态估计能力。
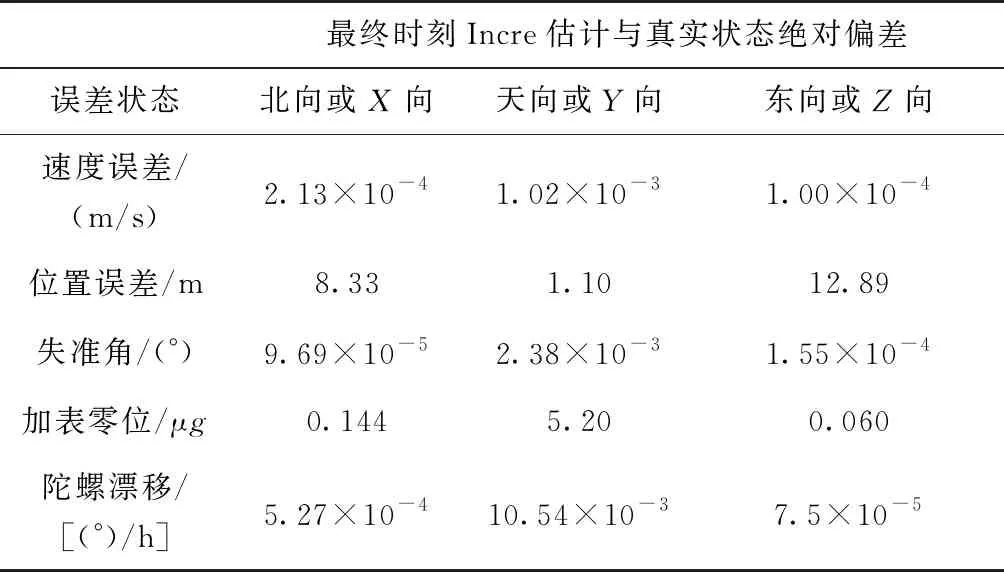
表2 Incre估计与真实状态对比
本文S_Incre选取“窗口为20,20进10”的滑窗方式,以验证滑窗维持运算速度稳定的能力。当状态量个数为20时,在添加新状态前需要滑掉前10个状态,保留后10个状态,添加新状态依然使用增量推断。
由图4可知,该滑窗方式下,不使用滑窗与使用滑窗的状态估计曲线近乎重合,且由表2与表3可知,最终时刻不滑窗估计、滑窗估计与真实状态的绝对偏差相当。

表3 SIncre估计与真实状态对比
文中实现的全局推断、增量推断及滑窗增量推断在相同处理器下运行,且均运行三次及以上,求取平均运行时间,如表4所示。标***表示运算时间过长,超天量级。

表4 运行时间
由表4中的运行时间可知,当处理5min的仿真数据时,全局推断耗时24h15min59s,而增量推断仅耗时2.074s。对于一元观测因子图模型,与全局推断相比,增量推断算法对运算速度提升明显。但是随着状态个数的不断增加,处理仿真数据(1min)的平均时间不断上升,与理论分析结果一致。使用滑窗后,滑窗内的状态个数至多20个,处理仿真数据(1min)的平均时间在0.15s左右,运行时间呈线性增长,验证了滑窗使运算速度维持稳定的能力。
5 结论
本文开展了基于因子图的状态估计方法运算实时性研究,主要工作如下:
1)研究了因子图算法中的消元算法,并使用该算法分析了一元观测因子的因子图模型,结合增量推断思想,提出了一种适用于该模型的增量推断算法;以静基座条件下速度匹配为例,通过数学仿真,与真实状态进行对比,验证了该算法的状态估计能力;与全局推断进行对比,验证了该增量推断算法对于求解一元观测因子图模型的状态估计问题的运算速度提升能力;
2)结合该增量推断算法,研究了基于固定滞后平滑算法的滑窗实现方法,通过数学仿真,该滑窗实现方法使运行时长呈线性增长,从而验证了该滑窗维持运算速度稳定的能力。

