基于融合云模型分析的时间序列概念划分方法

李金武，王清珍

(郑州科技学院 信息工程学院，河南 郑州 450064)

随着社会经济和信息化技术的发展，如何从海量数据中挖掘出有价值的信息服务于国家发展，一直是研究的热点[1-4]。时间序列应用广泛，是数据挖掘的重点研究对象，相较于传统数据挖掘，基于时间序列的数据挖掘需要考虑时间维度上数据的变化趋势，分析相邻数据的关联性。如何全面提取时间序列关键特征，获取有价值的信息，进而对其进行有效评估，是基于时间序列的数据挖掘研究需要重点考虑的问题。

时间序列通常每隔一段时间采样一次，导致数据具有随机性和模糊性等特点，故对时间序列概念进行合理划分是保证其有效评估的前提。概念划分一般采用两种方法[5-6]：一种是硬性划分，通过计算数据极差，将概念论域硬性划分为不重叠的区间，该方法提取到的规则不符合人们的思维过程，整个概念聚类过程没有体现数据随机性和模糊性特征，弱化了决策评估的实际意义；另一种是软划分，根据数据实际分布将概念论域划分成有重叠的区间，把定量数据转换成定性概念，保留数据随机性和模糊性特征，显然这种概念软划分方法对决策评估有重大实际意义。刘玉超[7]提出用云模型数字特征表示的概念含混度来度量概念共识度，利用高斯混合模型实现云变换算法，计算概念云数字特征，算法仅实现一维数据的概念提取。刘旋等[8]对文献[7]提出的方法进行了改进，通过K均值聚类算法对概念粒度进行初始化，使用综合云对概念粒度进行跃升，将确定度与欧氏距离相结合，对所属概念粒度进行划分。许凯等[9]打破启发式云变换仅对一维数据进行处理的限制，在高斯混合模型基础上，借助高斯分布拟合误差求解云模型数字特征，实现了多维数据云变换及概念提取。邓伟辉[10]提出了一种基于二维正态云的时间序列粒化降维方法，对时间序列进行二维处理，并利用云模型进行相似性度量。代劲等[11]从煤矿安全监管需求出发，面向煤矿安全大数据，提出宏观、微观、时间和空间的概念表示方法，利用云模型实现定量与定性之间的不确定性转换，满足了安全监管的变粒度需求。由于时间序列的不确定性及其自身线性特征，概念划分需要包含随机性和模糊性，并且应体现时间序列线性变化趋势，但上述文献并没有对时间序列概念进行有效划分。为解决此问题，本研究从时间序列本身及其变化趋势出发对时间序列进行多维处理，并利用高斯混合模型云变换算法将时间序列划分为由多个云模型表征的定性概念，从而实现了时间序列从定量数据到定性概念的不确定性转换。

1 时间序列多维处理

时间序列是按时间排序的一组变量数据，通常每隔一段时间采样一次，本质上反映了随时间变化的趋势，故对时间序列进行概念划分时，应对其进行多维处理，提取变化趋势特征。在时间序列中，通常用两个重要数据分布描述其特性，即原始序列频率分布和差分序列频率分布。基于以上思想，将一维特性原始时间序列转换为二维序列，既保留了原始数据特征，又表征了时间序列随时间变化趋势。处理方法如下：

给定含有n个观测值的时间序列T=(t1，t2，t3，…，tn)，计算其一阶差分序列ΔT，即

(1)

得到n个二维数据，即处理后的时间序列，表示为(T，ΔT)=((t1，e1)，(t2，e2)，(t3，e3)，…，(tn，en))。

2 云模型理论

时间序列经过二维处理以后，利用云模型进行概念软划分，最大限度提取时间序列特征值。云模型是在概率论和模糊数学的基础上，对随机性和模糊性及其关联性进行深入研究后提出的理论模型[12-13]，定义如下：设U是一个论域空间，C是U上一个定性概念，用数字特征Ex、En、He表示。对于任意x∈U，且x是定性概念C上的一次随机实现，则x对于C的确定度y=u(x)是一个具有稳定倾向的随机数。把(x，y)在U上的分布称为云，x称为云滴。

上述定义中论域空间维度可以是任意的，对应一维云模型C(Ex，En，He)，二维云模型C(Ex，Ey，Enx，Eny，Hex，Hey)和多维云模型C(Ex，Ey，…，Enx，Eny，…，Hex，Hey，…)。当论域空间为一维时，Ex是云模型的数学期望，代表论域空间云滴正中心，En是云模型的熵，反映论域空间云滴离散程度，He是云模型的超熵，表示熵的不确定度，反映云滴厚度。曲线y表示一维正态云模型期望曲线：

(2)

当论域空间为二维时，期望(Ex，Ey)表示二维正态云模型在平面XOY投影的形心，是最能够代表定性概念的点，熵(Enx，Eny)表示二维正态云模型在OX轴和OY轴方向上“亦此亦彼”的裕度，超熵(Hex，Hey)表示二维正态云模型在平面XOZ和平面YOZ投影的离散程度。曲线z1和z2表示二维正态云模型在平面XOZ和平面YOZ投影所形成的一维正态云模型期望曲线：

(3)

3 云模型概念划分

时间序列多维处理后，服从二维正态分布。利用二维高斯混合模型划分多个高斯分布并对其进行云变换，提取时间序列云模型定性概念。

3.1 高斯混合模型算法

以二维数据为例，假设样本数据X=(x1，x2，…，xn)T，xi=(xi1，xi2)，1≤i≤n，为二维数据，且服从二维高斯分布，其概率密度函数

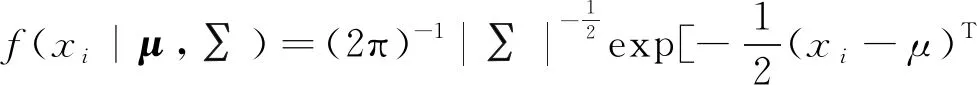
(4)

式中：μ是一个二维均值向量，由二维高斯分布样本期望描述；∑是一个2×2协方差阵，由高斯分布样本方差描述，|∑|是∑的行列式。

高斯混合模型由多个高斯分布线性叠加而成，假设有K个高斯分布，则高斯混合模型由这K个高斯分布按照不同概率混合，其数学表示形式如下：

(5)

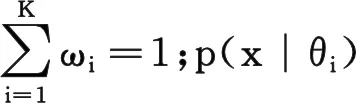
对于参数Θ的估计采用最大期望值(EM)算法[14-15]。为减少迭代次数与计算量，首先使用K均值聚类算法[16-17]对高斯混合模型初始化，再运用EM算法进行参数计算。

算法1高斯混合模型算法。

输入：n个样本数据X=(x1，x2，…，xn)T，xi=(xi1，xi2)，1≤i≤n。

输出：K个高斯分量。

步骤1使用K均值聚类算法对高斯分布参数进行初始化，K值利用手肘法[16]确定：

步骤2E-step，用初始化参数计算后验概率：

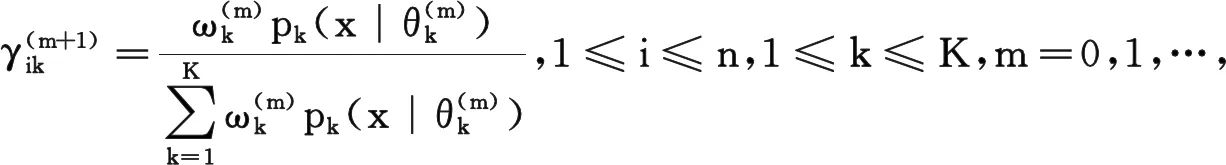
步骤3M-step，用后验概率计算新参数Θ(m+1)：

步骤4重复步骤2和步骤3，直到算法收敛。

3.2 云变换算法

云变换是依据数据频率分布特征进行粒化，划分定性概念的一种过程[18]。将数据频率分布曲线分解成若干个正态云模型的叠加，实现定性概念软划分，每个定性概念统一用云模型数字特征表示。数学表示形式如下：

(6)

式中：f(x)为频率分布函数；ai为云模型幅度系数；n为云模型个数。

本研究使用基于高斯混合模型的云变换，利用高斯混合模型对时间序列进行建模。将时间序列分解成若干个高斯分布叠加，利用高斯分布拟合误差求解云模型数字特征，再将高斯分布函数转换成云模型，实现时间序列概念划分。此方法不仅可以实现一维数据概念划分，还可实现多维数据概念划分。

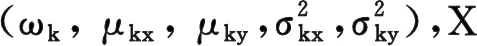
算法2云变换算法。

输出：定性云模型参数C(Exk，Eyk，Enxk，Enyk，Hexk，Heyk)，1≤k≤K。

步骤1令Exk=μkx，Eyk=μky，Enxk=σkx，Enyk=σky。

步骤2计算X和Y的边缘概率密度函数：

步骤3计算：

步骤4计算：

步骤5计算：

步骤6计算：

4 实例验证

为有效分析时间序列概念划分效果，本研究采用真实数据集进行实验仿真。仿真分析选用MATLAB软件，数据集为某交通卡口一天实际交通流量，共包含288条数据，记录交通卡口4条车道车流量状态，从0∶00到23∶55每隔5 min记录一次。

4.1 数据二维处理

对于时间序列，利用原始数据提取趋势变化数据，将单一属性数据变为双属性数据。其中，车流量原始数据如图1所示。利用公式(1)对时间序列进行二维差分处理，一阶差分数据如图2所示。

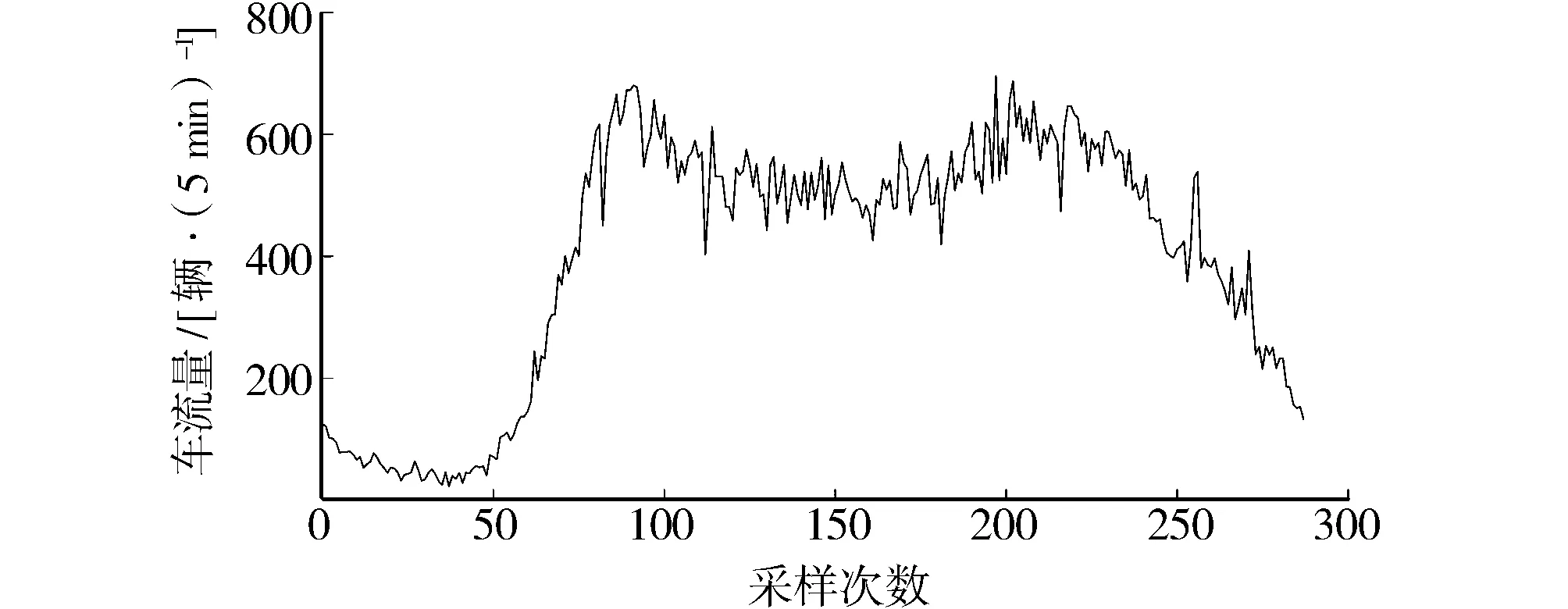
图1 车流量原始数据Fig.1 Original data of the traffic flow

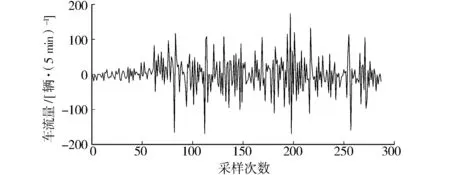
图2 车流量一阶差分数据Fig.2 First-order difference data of the traffic flow

车流量原始数据频率分布见图3。当车流量低于100辆/5 min或高于400辆/5 min时，数据分布相对比较密集，符合车流量凌晨和日间高峰时段运行状态。车流量一阶差分数据频率分布见图4，车流量一阶差值为-25～+25时，数据分布相对比较密集，说明大部分时间段车流量变化趋势比较稳定。整体数据频率分布符合车流量实际情况。

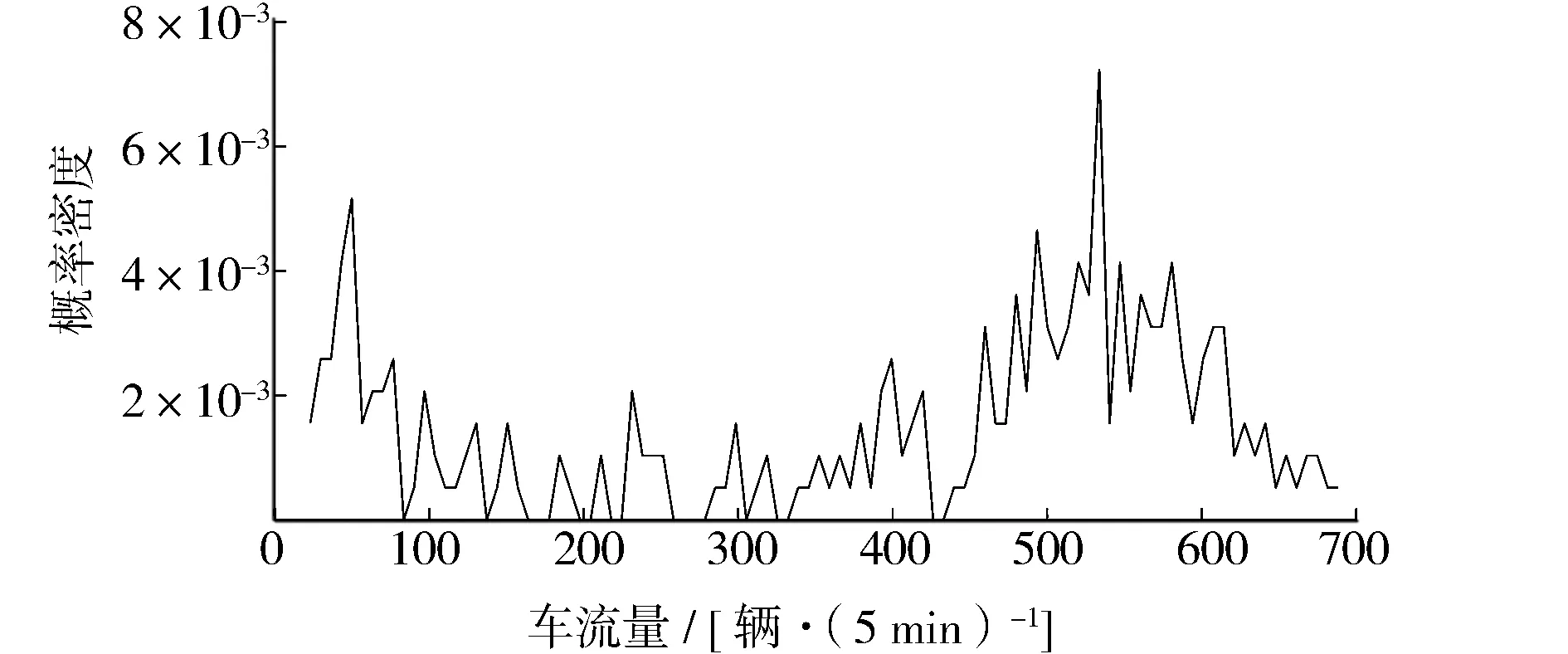
图3 车流量原始数据频率分布Fig.3 Frequency distribution of original data of the traffic flow

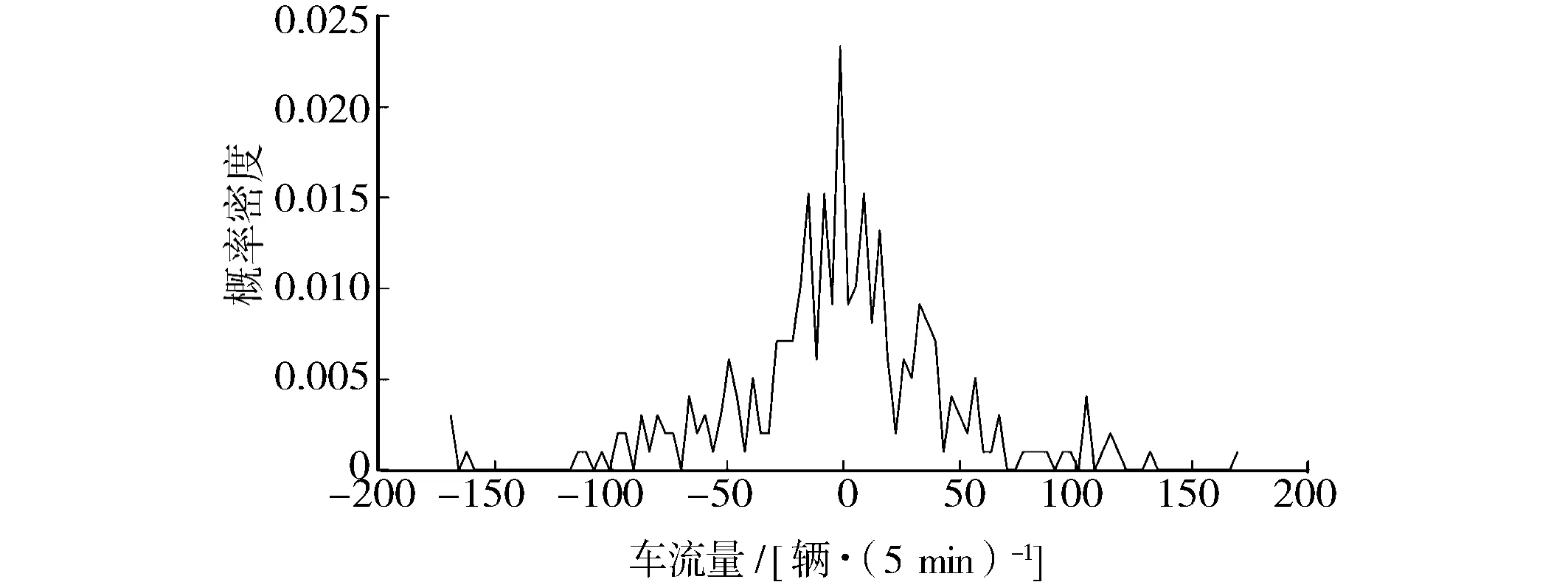
图4 车流量一阶差分数据频率分布Fig.4 Frequency distribution of first-order difference data of the traffic flow

为了直观展示处理后的二维数据，选用三维空间散点图。在散点图(图5)中，一个点代表一个时间序列观测值。散点图在平面坐标的投影如图6所示。

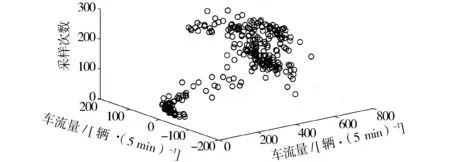
图5 三维空间散点图Fig.5 Three-dimensional scatter plot

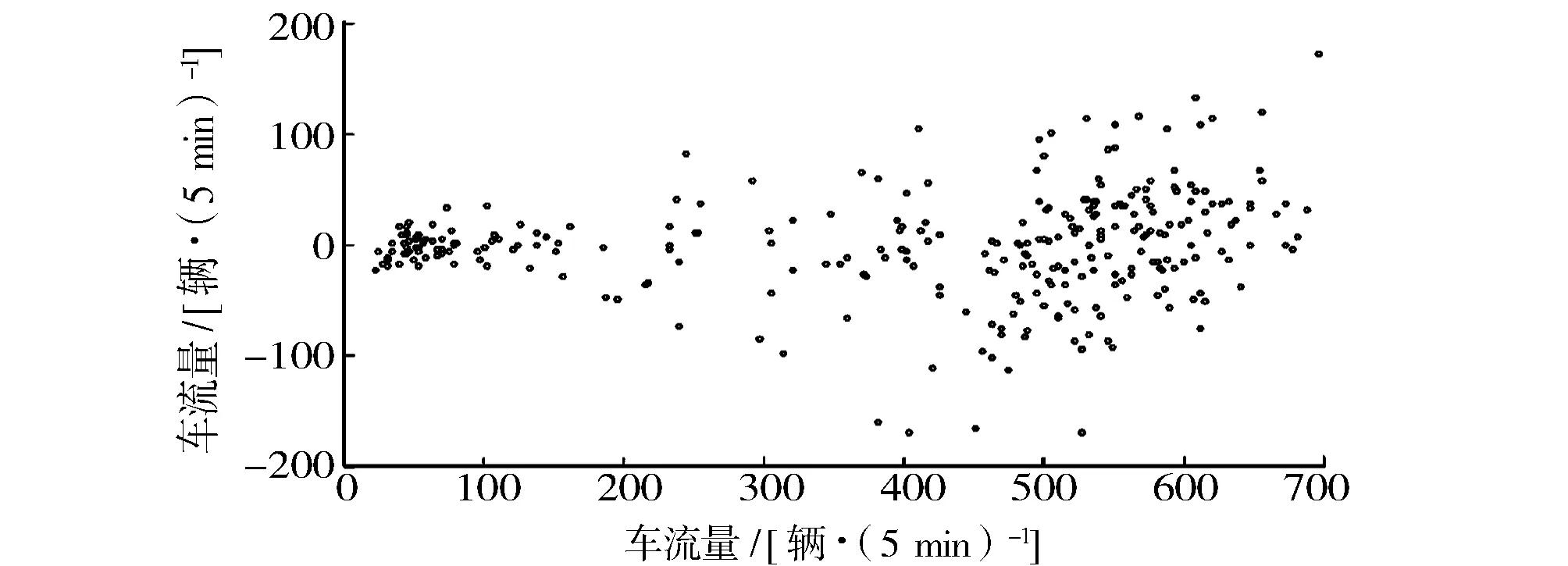
图6 散点图投影Fig.6 Projection of three-dimensional scatter plot

4.2 概念提取

综合考虑车流量状态和变化趋势二维属性，对交通卡口车流量变化进行概念提取。首先，利用算法1对高斯混合模型进行分解，得到5个高斯分布线性叠加，其中高斯分量个数利用K均值聚类手肘法确定。5个高斯分量参数值如表1所示。

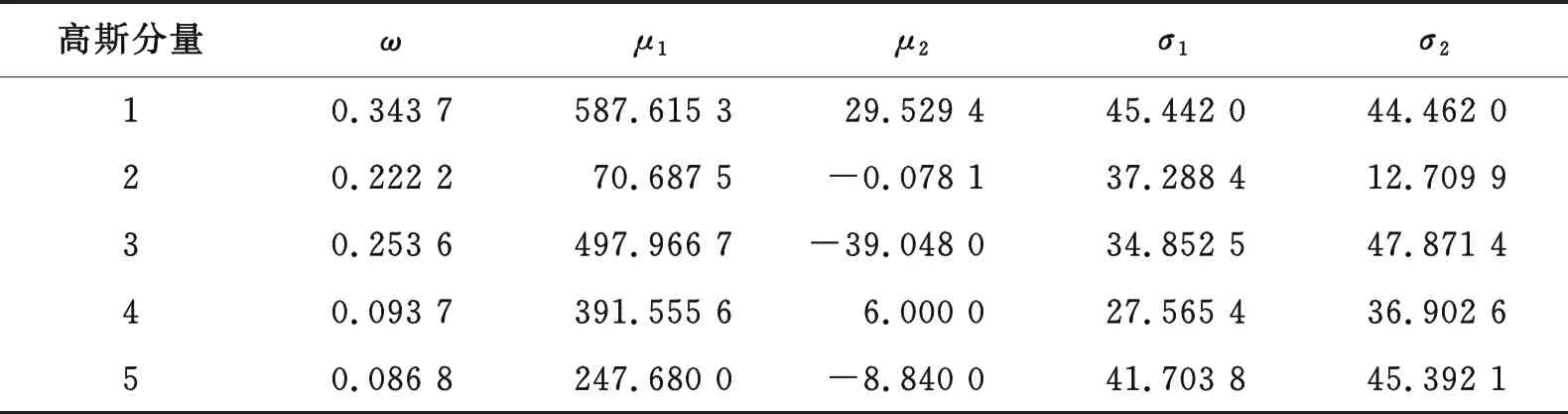
表1 高斯分量参数值Tab.1 Parameter value of Gaussian component

然后，利用算法2对表1中5个高斯分量进行云变换，得到5个概念云，其云模型数字特征见表2。由云数字特征刻画概念云标尺及其投影，如图7与图8所示。

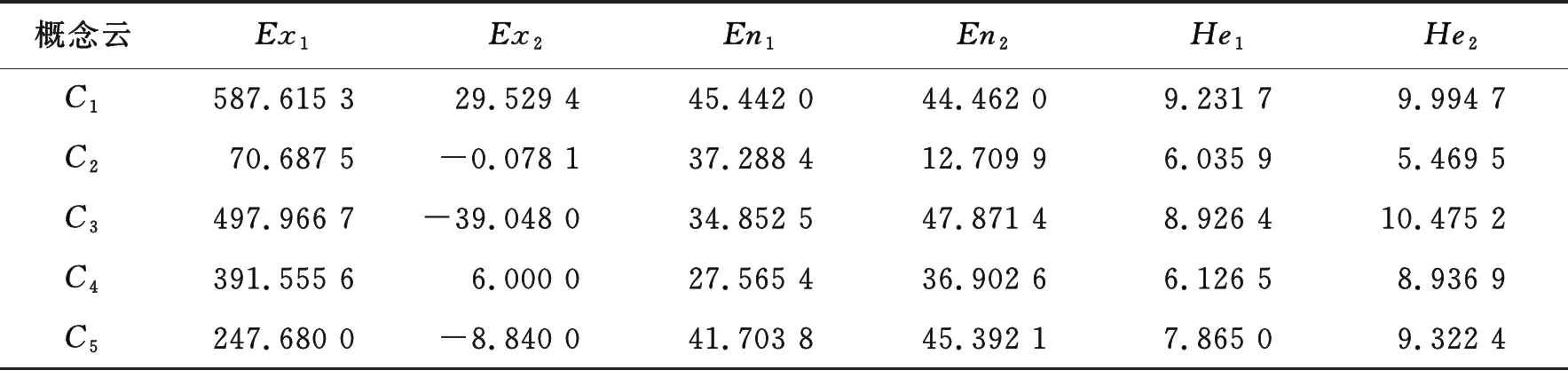
表2 云模型数字特征Tab.2 Digital features of cloud model

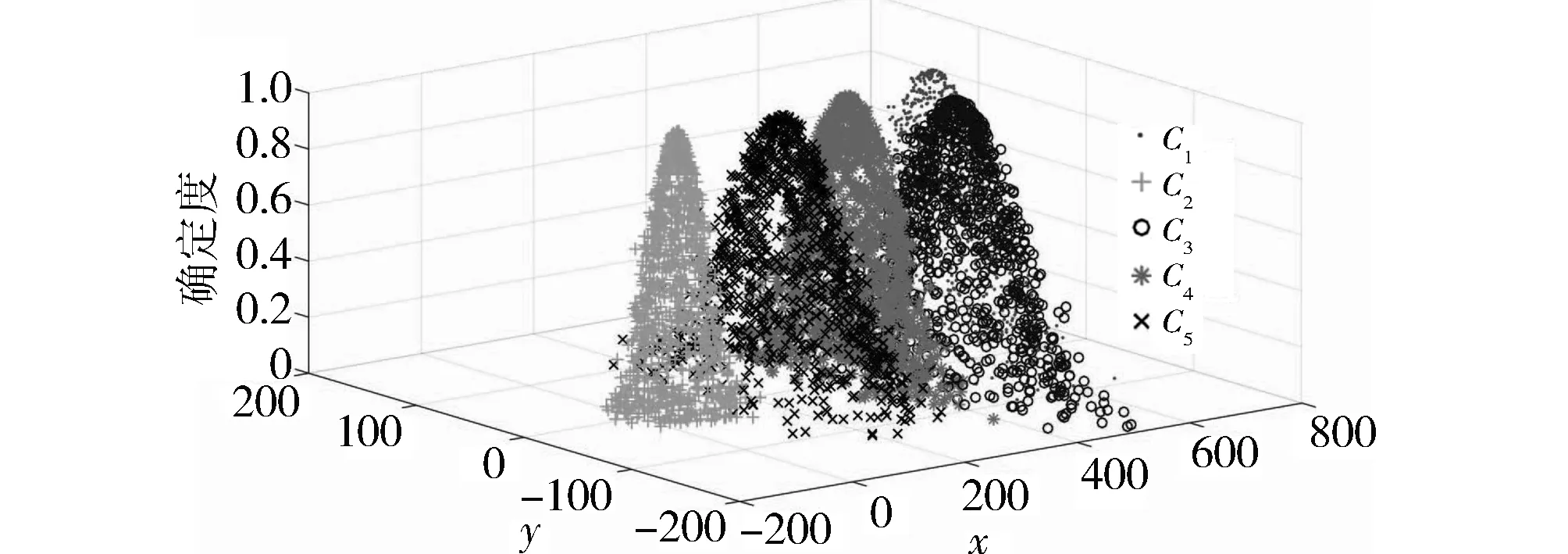
图7 概念云标尺示意图Fig.7 Diagram of concept cloud scale

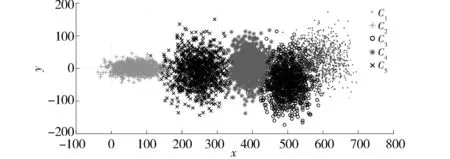
图8 概念云标尺投影Fig.8 Projection of concept cloud scale

概念云标尺表征的5个概念反映了车流量大小和车流量增速不同状态。概念云C2表征的概念说明车流量较小且变化趋势较稳定，概念云C1表征的概念说明车流量较大且变化趋势明显。仅从车流量变化趋势分析，概念云C2趋势稳定，概念云C1和C3趋势有一定波动，有效反映了凌晨时间段和日间高峰时间段车流量实际状况。

表3 本方法与A-GCT比较结果Tab.3 Comparison results between this method and A-GCT

4.3 对比分析

本方法与文献[7]中自适应高斯云变换(A-GCT)相比，采用K均值聚类手肘法确定高斯分量个数，克服了A-GCT方法初始粒度选取的盲目性，减少了迭代次数，使得EM算法收敛速度更快，效率明显提高。并且，本方法不仅适用于一维数据，而且适用于多维数据，在数据普适性、概念误分率和时间复杂度上均有明显改善。具体比较结果见表3。

5 结语

本研究提出的概念划分方法，基于高斯混合模型实现云变换，可以有效对时间序列进行概念划分，体现了数据的随机性和模糊性，实现了时间序列定量数值到定性概念的不确定性转换。实验结果表明，本方法在原始数据属性上增加了序列变化趋势属性，利用二维云变换算法进行概念提取，较仅考虑原始数据单一属性提取的概念更符合实际。