基于扩展有限元分析的页岩水力压裂裂缝扩展规律探究

温继伟，项 天，朱 茂，胡 萍，毛建设，荆羽慧

（1.石家庄铁道大学土木工程学院，河北 石家庄 050043；2.成都理工大学环境与土木工程学院，四川 成都 610059；3.中石化中原石油工程有限公司管具公司，河南 濮阳 457300）

0 引言

随着世界经济和社会的持续高速发展，人们对能源的需求与日俱增；然而，石油、天然气等常规能源的产量已难以满足现代社会的需求，因此，对于非常规能源的开发已成为人们广泛关注的焦点［1-3］。页岩气作为非常规天然气资源之一，其发展潜力十分巨大，中国的页岩气资源丰富，但相应的开采技术起步较晚，故与美国等世界发达国家相比尚有一定的差距［4-6］。相比于常规天然气，对地下页岩气的开采更为复杂，其开采技术的发展也颇具难度；目前的页岩气开采主要为水力压裂技术，通过向地下注入压裂液，使得水力裂缝在页岩储层中扩展，从而有效建立页岩气的采气通道，探索水力裂缝在页岩储层中的扩展规律，是实现页岩气增产的有效途径［7-8］。陈勉［9］运用断裂力学推导了水力裂缝扩展的控制公式，并结合实例计算，研究了原始地应力、压裂液排出速率和粘度、压裂主缝与天然裂缝的初始逼近角度对裂缝扩展的影响。王聪等［10］通过室内页岩水力压裂实验和数值模拟的方法，探究了农安矿区油页岩的破裂压力，得到了模拟值、实验值较计算值均偏大的结论。侯振坤等［11］利用真三轴物理模拟实验，研究了大尺寸页岩水力裂缝的形成机理，结果表明，页岩中存在的弱结构面是水力压裂过程中形成复杂缝网的主要影响因素。周彤等［12］通过室内岩石力学实验测得页岩的力学各向异性特征，结合离散元方法研究了层理对水力裂缝扩展的影响，表明高密度层理缝会明显增加水力裂缝的复杂性，并且会显著限制水力裂缝的缝高。Jafari A等［13］提出了一种新型的流体力学完全耦合模型，用于评估失水量对饱和多孔介质压裂效率的影响。

现有研究主要存在以下问题：（1）水力压裂裂缝扩展的研究多数集中在单条裂缝，对于多条裂缝分时段起裂的相关研究较少；（2）层理的岩性、构造方向和内部倾角对页岩水力压裂裂缝扩展路径影响显著，目前研究多数集中在层理构造方向对页岩水力压裂裂缝扩展路径的影响，针对不同岩性层理和内部倾角如何影响裂缝扩展的研究较少。针对上述问题，本文基于ABAQUS中的扩展有限元方法（Extended Finite Element Method，XFEM），对均质页岩情况下水力压裂裂缝扩展形成单条裂缝和多条裂缝时的扩展规律，对含层理页岩情况下层理构造方向、内部倾角和层理岩性如何影响裂缝扩展分别展开探究，相关结果可为页岩气的高效开采提供一定的参考依据。

1 页岩数值模型建立与验证

1.1 数值模型建立

参照文献［14］和文献［15］中页岩数值模型的建立方法，在ABAQUS软件中分别建立均质页岩（无层理）、含45°方向构造层理的页岩、含水平构造层理的页岩和含竖直构造层理的页岩4种模型，如图1所示。不同页岩模型的规格均为60 m×60 m；不同层理的厚度均为5 m且等间距布设；不同模型的初始裂缝长度均设为1.5 m。均质页岩模型的初始裂缝位置设有由如图1（a）所示的3种单条裂缝工况和多簇压裂工况，后文有详细工况介绍，在此不多做赘述。一般情况下，层理的力学性质要弱于页岩，此时若层理的构造方向与主应力方向存在偏差，水力裂缝扩展至层理处容易沿层理内部扩展［15］。为了探究裂缝在不同岩性层理内部的扩展规律，建立如图1（b）所示模型；为了更为准确直观地观察层理内部倾角变化对垂向裂缝扩展的影响，选取2种最特殊的层理构造方向（即水平和竖直）建立模型，如图1（c）、图1（d）所示，并在软件中改变层理材料方向与最大水平地应力方向的夹角来模拟层理内部倾角。地层所受最大水平主应力σH方向均为X方向（数值可取5、6、7 MPa），最小水平主应力σh方向为Y方向（数值均为5 MPa），如图2所示。模型的左右竖直两边约束X方向位移，上部边约束Y方向位移，下部边设为对称约束。页岩和层理的主要力学参数如表1所示［15-16］，压裂液粘度均为0.06 Pa·s，注入压裂液的体积流量均为0.001。

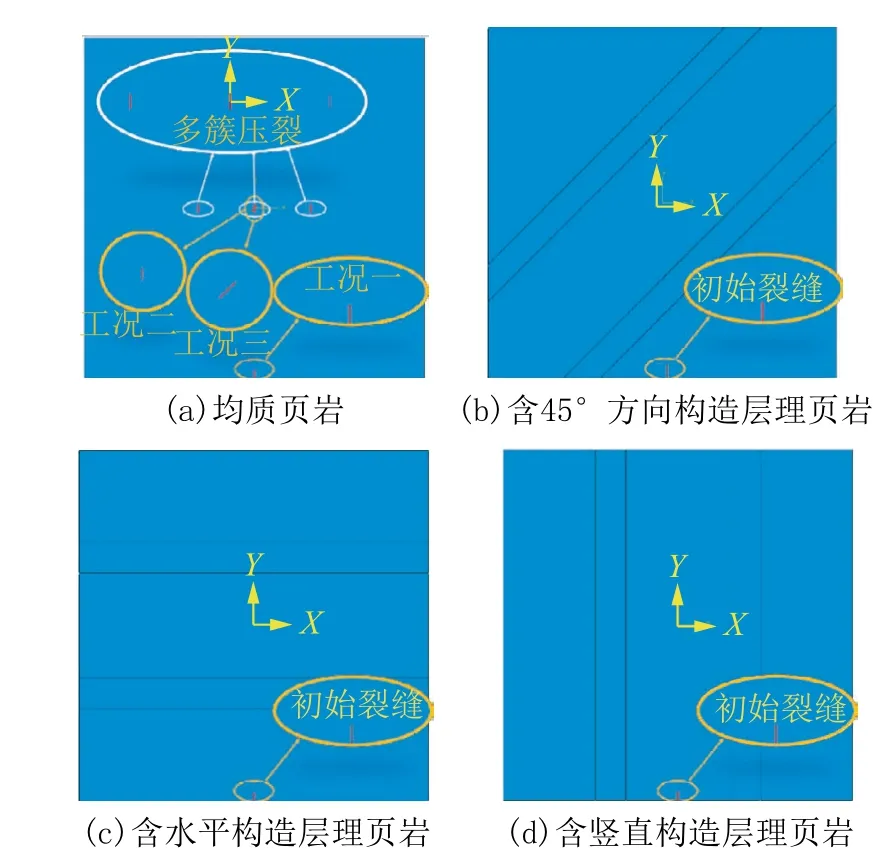
图1 页岩模型示意Fig.1 Schematic diagram of the shale models

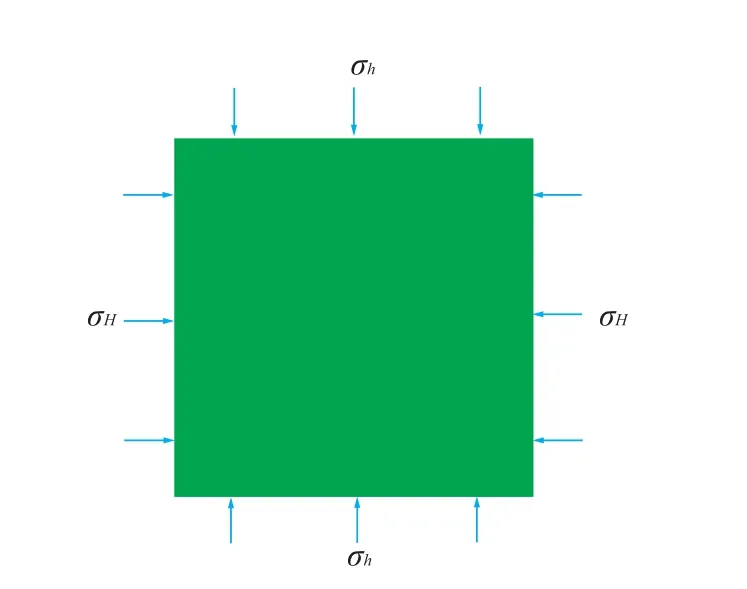
图2 页岩所受地应力示意Fig.2 Schematic diagram of ground stress on shale

表1 页岩和层理的力学参数[15]Table 1 Mechanical parameters of shale and bedding

1.2 数值模型验证

为了检验模型的可靠性，以姜浒等［17］运用大尺寸真三轴水力压裂物理模拟实验系统进行水力压裂试验为基础，模拟同一条件下的裂缝扩展路径。数值验证模型的尺寸与物理模拟试验保持一致，为0.3 m×0.3 m，为图1（a）中工况三下的均质页岩模型的缩小模型。其最大水平主应力方向为X方向（6 MPa），最小水平主应力为Y方向（1 MPa），射孔方位角为60°，验证模型所用材料参数为：材料属性为页岩，弹性模量8.402 GPa，泊松比0.23，抗拉强度2.59 MPa。

模拟结果与物理模拟试验结果对比如图3所示。从图3可以发现二者裂缝扩展路径大体保持一致，裂缝扩展规律基本吻合，说明采用扩展有限元法模拟水力裂缝扩展具有较高的可靠性。

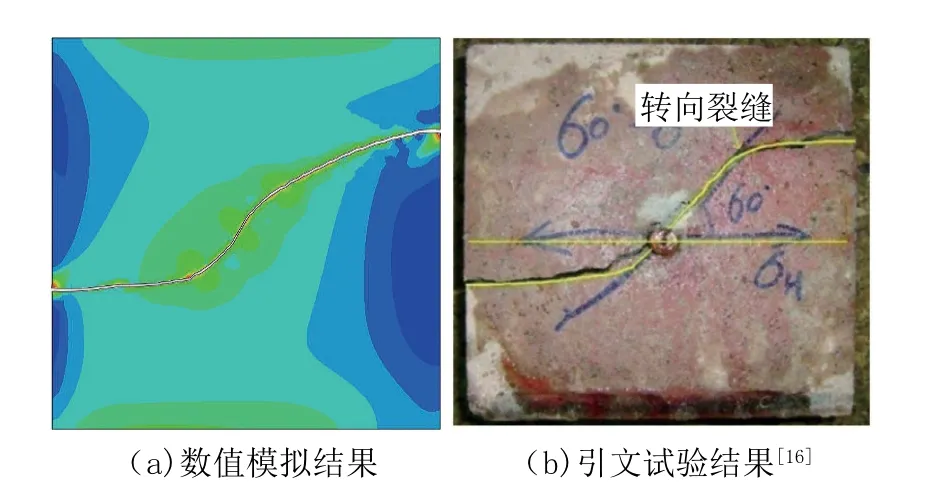
图3 数值模拟与物理模拟结果裂缝扩展路径对比Fig.3 Comparison of fracture propagation paths between numerical simulation and physical simulation results

2 均质页岩水力压裂裂缝扩展规律

对于均质页岩水力压裂裂缝扩展规律的研究包括如表2所示的3种工况，探究当地应力差△σ分别为0、1和2 MPa时所对应的不同工况下裂缝的扩展规律。其中，初始裂缝位置可设为页岩模型底边的中部或页岩模型的中部，注液点位置可设为初始裂缝底端或中部，初始裂缝与最大水平主应力方向的夹角（以下简称为“方位角”）可设为90°或45°。各工况下裂缝扩展的数值模拟结果如图4～6所示。

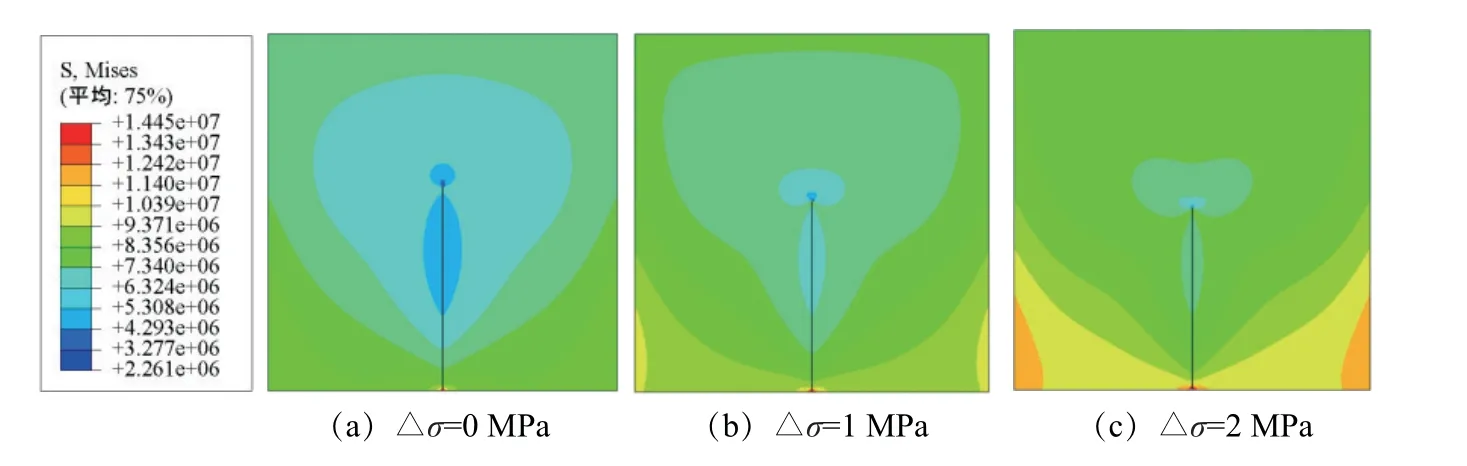
图4 工况一下的裂缝扩展云图Fig.4 Nephogram of fracture propagation under the working condition 1

表2 不同工况参数Table 2 Parameters of the different working conditions

2.1 裂缝扩展长度和方向

由图5可知，在工况二中的初始裂缝在水压作用下沿着原方向在均质页岩中分别向两端扩展，这种扩展方式比工况一中的初始裂缝仅向一端扩展的更长。如表3所示，与工况一下的裂缝扩展长度相比，当地应力差为0 MPa时，工况二下的裂缝扩展长度增加了11.2 m，增幅为32.6%；当地应力差为1 MPa时，工况二下的裂缝扩展长度增加了8.9 m，增幅为27.9%；当地应力差为2 MPa时，工况二下的裂缝扩展长度增加了7.9 m，增幅为25.9%。由此可知：对于工况一和工况二，当初始裂缝垂直于最大水平主应力方向扩展时，随着最大水平主应力的增加，裂缝的扩展变得更困难，其扩展长度变短，且在注液体积流量相同的情况下，裂缝向两端同时扩展优于裂缝仅向一端扩展，但当地应力差逐渐变大时，该趋势会有所降低。

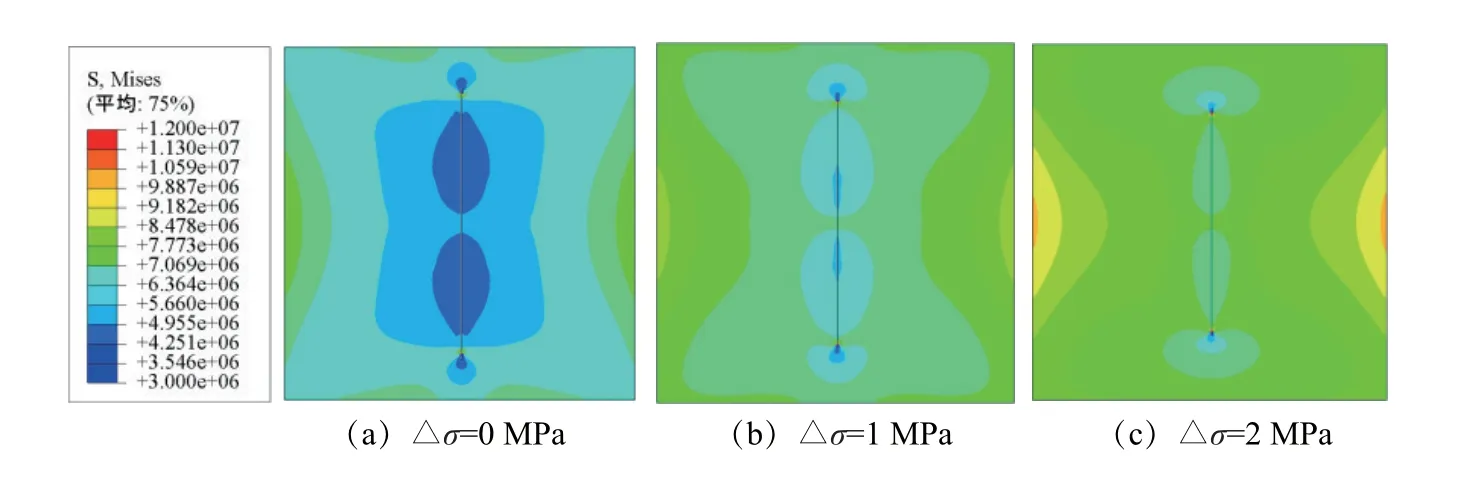
图5 工况二下的裂缝扩展云图Fig.5 Nephogram of fracture propagation under the working condition 2

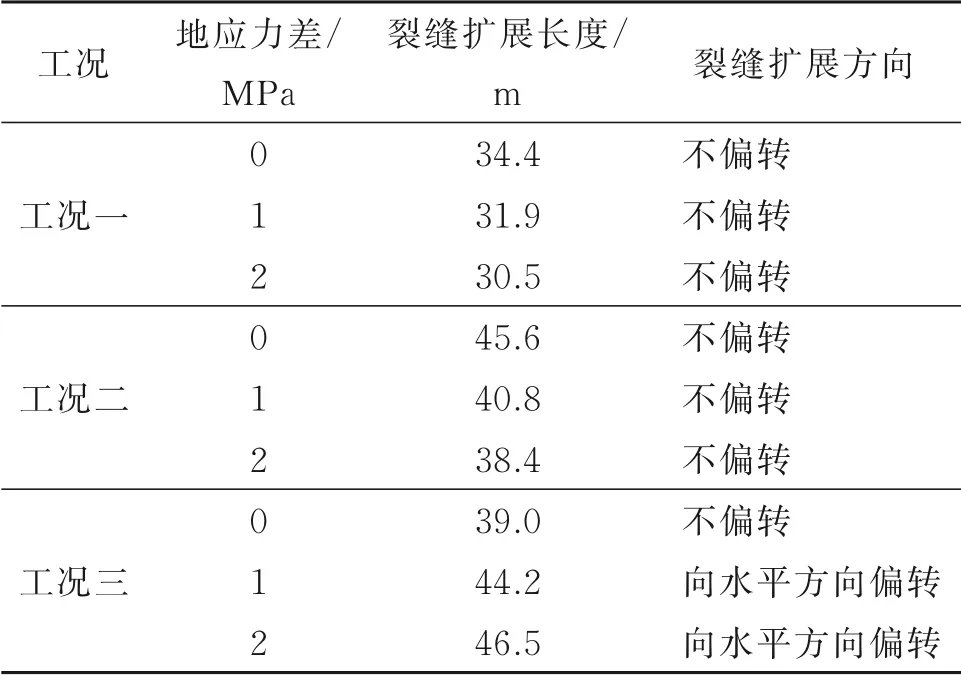
表3 各工况下裂缝扩展方向与长度统计Table 3 Fracture propagation direction and length under the various working conditions

由图6可知，当地应力差为0 MPa时，初始裂缝沿着原方向继续扩展，但当最大水平主应力逐渐增大时，裂缝将朝着最大水平主应力方向发生偏转，且裂缝的偏转程度随着地应力的增大而增大；当地应力差为1 MPa时，裂缝的扩展长度比地应力差为0 MPa时增加了5.2 m，增幅为13.3%，当地应力差为2 MPa时，裂缝的扩展长度比地应力差为1 MPa时增加了2.3 m，增幅为5.2%。由此可知：工况三的裂缝扩展规律和工况二时不同，当方位角为45°且存在地应力差时，裂缝会向最大水平主应力方向发生偏转，并且裂缝的扩展长度随着地应力差的增大有所提升。

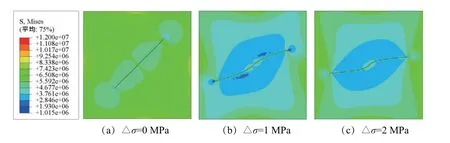
图6 工况三下的裂缝扩展云图Fig.6 Nephogram of fracture propagation under the working condition 3

2.2 裂缝扩展宽度和注液点压力

图7为各工况下注液点处的压力-时间及裂缝宽度-时间曲线，其中的实线为注液点处的压力随时间变化的关系曲线，虚线为注液点处的裂缝宽度随时间变化的关系曲线。

由图7中3种工况下注液点处的压力-时间曲线可知：（1）随着注液时间的增加，注液点处的压力迅速上升至峰值，曲线的峰值点可称为裂缝的起裂压力，注液点在达到起裂压力后开始起裂，随后注液点压力逐渐下降至某一值后趋于稳定，该值称为裂缝的扩展压力；（2）在工况一和工况二中，当裂缝垂直于最大水平主应力方向扩展时，随着最大水平主应力的增加，裂缝的起裂更为困难，裂缝的起裂压力和扩展压力都变得更大，并且初始裂缝向两端扩展时的起裂压力和扩展压力也明显比仅向一端扩展时更大；（3）在工况三中，当初始裂缝的方位角为45°时，3条压力-时间曲线基本一致，地应力差的改变对裂缝的起裂压力与扩展压力影响不大。

由图7中3种工况下注液点处的裂缝宽度-时间曲线可知：（1）不同工况下注液点处的裂缝宽度都是先在短时间内迅速增大，而后随着时间的增加而缓慢增加；（2）在工况一、二中，裂缝不偏转，并且裂缝宽度随着地应力差的增大而增大；（3）在工况三中，当地应力差为0 MPa时裂缝宽度最大，地应力差为1 MPa次之，地应力差为2 MPa最小，由此可知注液点处的裂缝宽度与裂缝长度也存在一种关系，即裂缝长度越长，注液点处的裂缝宽度越小，其原因是当注液体积流量和注液时间一定时，裂缝体积大致相同，裂缝若扩展的长度越长，则会使裂缝的宽度变小。

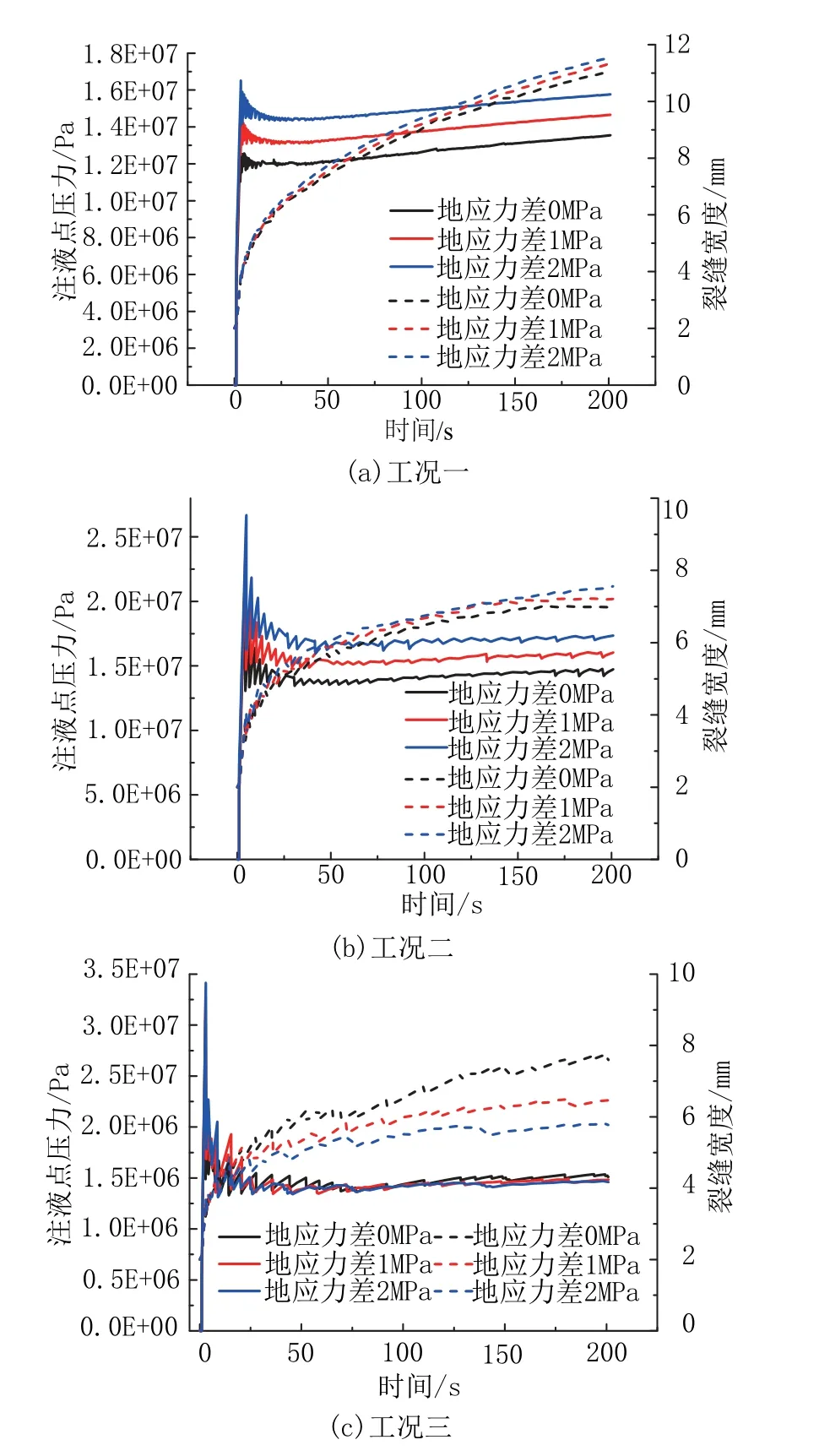
图7 各工况下注液点处的压力-时间及裂缝宽度-时间曲线Fig.7 Pressure vs time and fracture width vs time curves at the injection point under the various working conditions

为进一步探究裂缝宽度与裂缝长度之间的规律，在ABAQUS软件中选取3种工况均在地应力差为2 MPa下的裂缝起点、中点和终点3处的裂缝宽度进行对比研究，由于工况二和工况三是对称扩展，所以仅取裂缝上半部分的起点、中点和终点，结果如图8所示。由图8可知：对于裂缝未发生偏转的扩展路径（工况一和工况二），裂缝宽度的大小与裂缝上的某点和注液点（起点）间的距离有关，随着与注液点的距离增大，裂缝上某点的宽度减小；但对于出现偏转的裂缝扩展路径（工况三），其裂缝上某点的宽度并没有这种趋势，其起点和中点处的裂缝宽度大致相等，而在终点处的裂缝宽度较小。

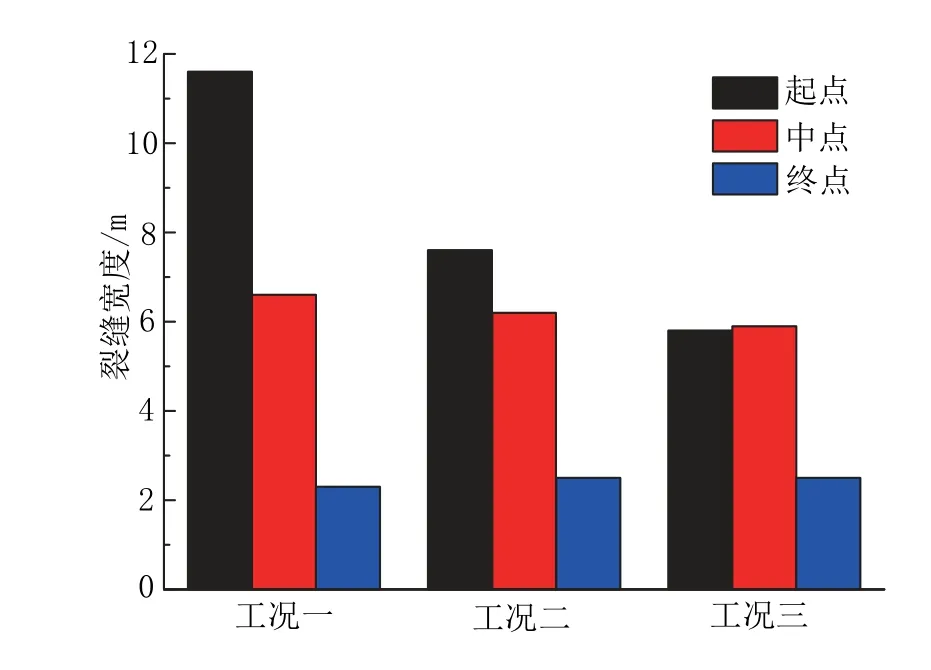
图8 各工况下裂缝上不同位置处的宽度对比Fig.8 Comparison of the width at different facture positions under various working conditions

2.3 多簇压裂裂缝扩展

水平井分段多簇压裂在实际油气生产过程中应用广泛。在压裂过程中，由于裂缝之间相互存在干扰，有利于出现复杂裂缝网络，从而提高油气储层的导流能力。本小节中对多簇压裂进行模拟研究。

数值模拟中射孔簇设置3个，采用分时进行压裂，压裂次序为：（1）页岩正中心射孔1；（2）位于射孔1正右侧、距离其10 m的射孔2；（3）位于射孔1正左侧、距离其10 m的射孔3。地应力差设置为0、2、4 MPa，其余模拟条件与前文一致，模拟结果如图9所示。

将在不同射孔下压裂产生的水力裂缝分别进行编号，结果如图9所示，将其在不同地应力差情况下各裂缝扩展长度进行统计，结果见表4。由图9可以看出，裂缝1由于是第一条压裂的裂缝，裂缝沿着初始裂缝方向扩展，并未出现裂缝扩展干扰现象。裂缝2、裂缝3由于是后压裂产生，页岩内部应力分布发生变化，裂缝扩展路径受裂缝1影响，各自朝远离裂缝1的方向扩展，并且在最大水平主应力的作用下，地应力差越大，其偏转程度越大。其原因如图10所示，先压开的裂缝会在其周围产生诱导应力场，改变原始页岩中的应力分布，使页岩内部最小主应力方向（即竖直方向）发生偏转，导致最小主应力方向和初始裂缝方向不再一致，成为裂缝偏转的诱因，使后续裂缝的扩展路径朝着最大水平主应力方向发生偏转。

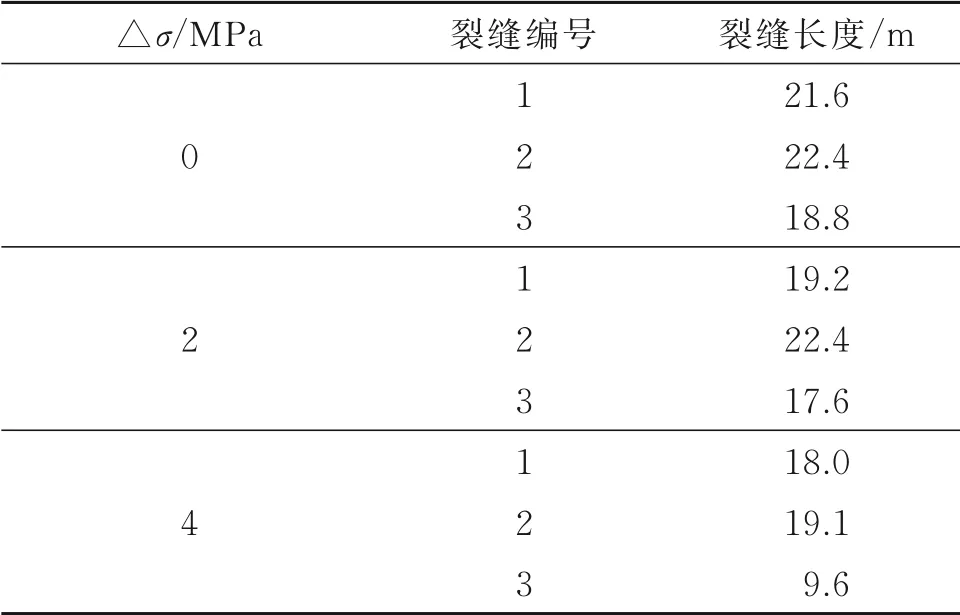
表4 不同地应力差下各裂缝长度统计Table 4 Fracture lengths under the different ground stress deviations

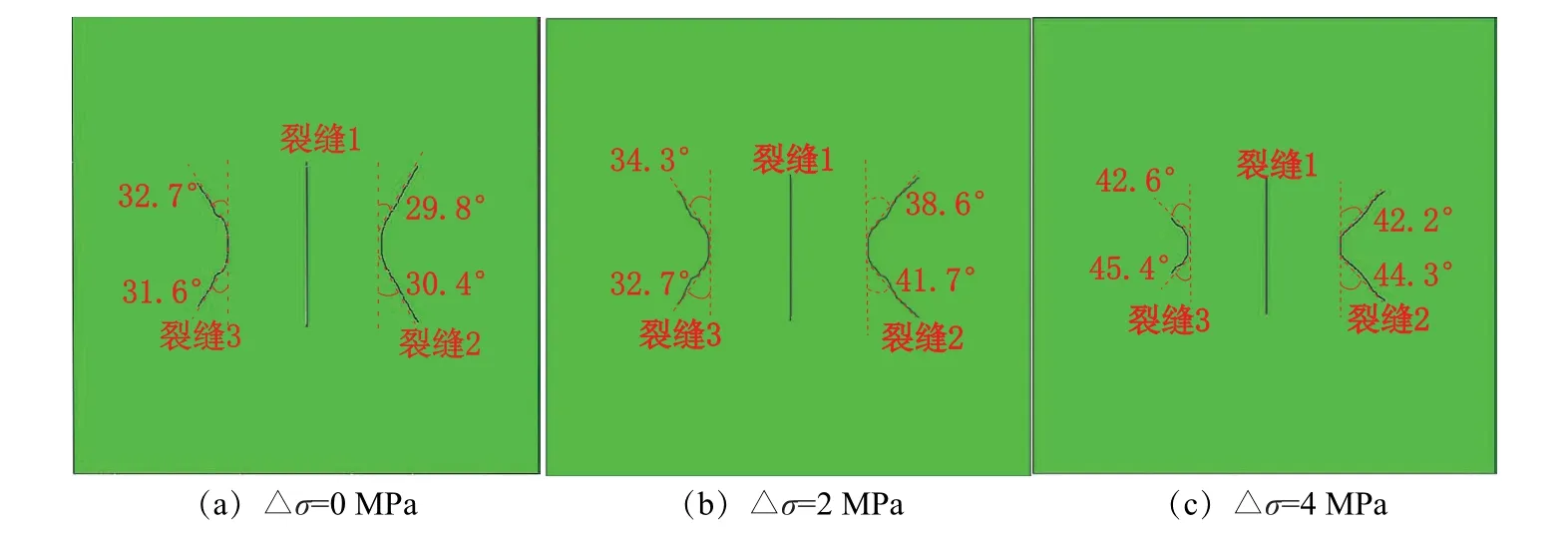
图9 三簇水力压裂裂缝扩展路径Fig.9 Fracture propagation paths of three-cluster hydraulic fracturing

由表4可知，对于不同地应力差下同一编号的裂缝，其地应力差越大，裂缝长度越短，这一规律同样也符合前文单簇下的规律。

3种地应力差下由于压裂次序的不同，使得3条裂缝的长度出现了同一现象，即裂缝1的长度大于裂缝3却小于裂缝2，出现该情况的原因为裂缝2在诱导应力场的干扰下，其向最大水平主应力方向发生偏转，在某种程度上这种偏转有利于裂缝扩展，导致裂缝长度会有不明显的增长趋势，但随着裂缝2压裂完成，裂缝间的诱导应力场越来越明显，如图10（c）所示，其内部应力场箭头颜色较裂缝1压裂完成时更深，页岩内部应力增大，从而使页岩更难压裂开，进而造成裂缝3更短的现象，表明压裂次序的不同会极大地影响各个裂缝的形态。

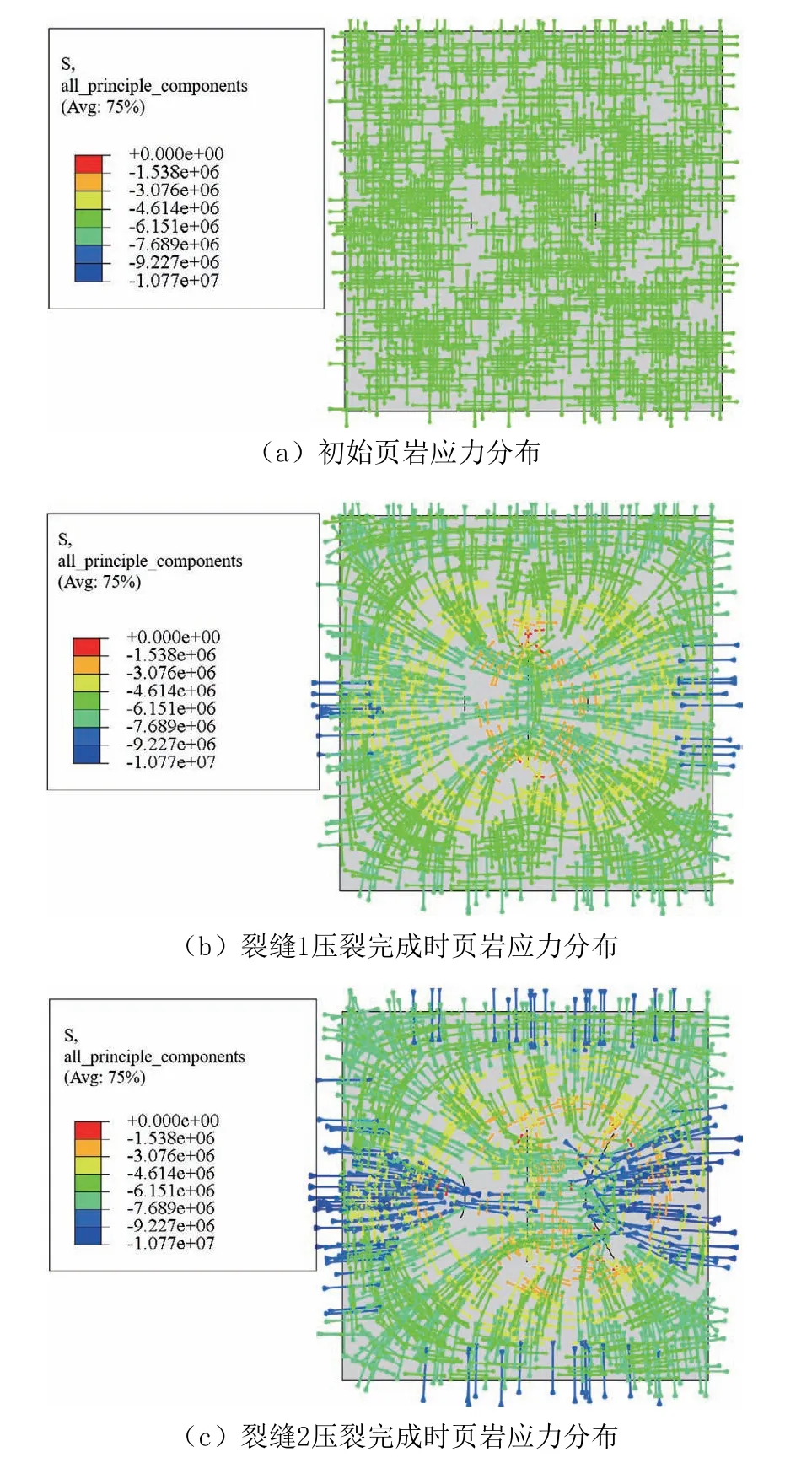
图10 各压裂阶段页岩内部应力分布Fig.10 Stress distribution in shale at each fracturing stage

选取地应力差△σ=2 MPa情况，对注液点压力与裂缝宽度进行分析，绘制时程曲线，结果如图11所示。对于注液点压力，裂缝1为第一条起裂的裂缝，其曲线的形态和起裂压力与前文工况二下情况保持一致；裂缝2和裂缝3在未开始注水阶段，注液点压力开始缓慢增加，并且由于裂缝1的形成，岩石内部应力分布发生改变，使得裂缝2和裂缝3注液点起裂压力增大，出现起裂更困难的现象；裂缝1和裂缝2的注液点裂缝宽度时程曲线形态大体一致，都是在页岩瞬间压裂时宽度陡增，然后随着压裂液的持续注入，裂缝宽度缓慢增加，当该裂缝压裂结束，停止注入压裂液后，由于“滤失作用”的存在，导致裂缝逐渐收缩，时程曲线中表现为缓慢下降段，裂缝3由于是最后压裂的裂缝，即没有停止注入压裂液阶段，所以曲线中没有缓慢下降段，并且起裂压力不同的是3条裂缝的裂缝宽度的峰值和起裂时所达到的瞬时宽度相差不大。这表明分时多簇压裂中，压裂次序对裂缝的起裂压力有着较大影响，即对比首次起裂，后续裂缝的起裂压力会相对增大，对各个注液点的裂缝宽度影响又相对较小。

3 层理构造对页岩水力压裂裂缝扩展的影响

为探究层理构造对页岩水力压裂裂缝扩展的影响，在ABAQUS中建立如图1（c）和（d）所示的含水平构造层理及含竖直构造层理的2种页岩模型进行对比研究，图12、图13为通过数值模拟得到的结果。

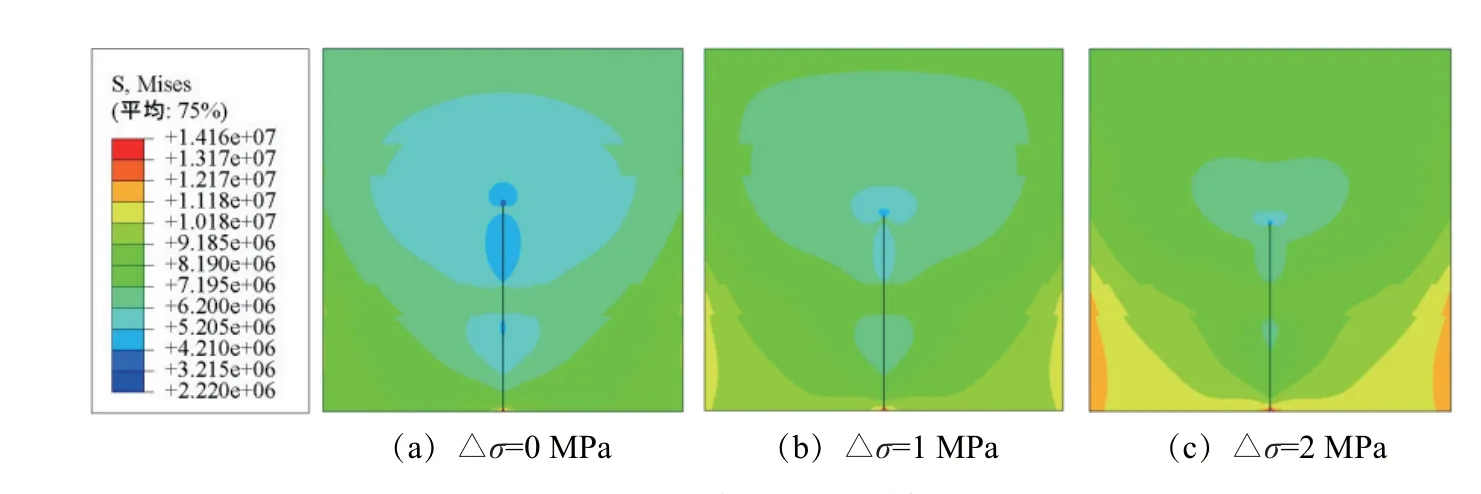
图12 水平构造层理下裂缝扩展云图Fig.12 Nephogram of fracture propagation under the horizontal bedding

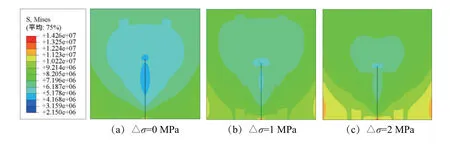
图13 竖直构造层理下裂缝扩展云图Fig.13 Nephogram of fracture propagation under the vertical bedding

3.1 裂缝扩展长度、注液点裂缝宽度及起裂压力

由图12、图13，统计含不同构造层理的页岩模型在地应力差分别为0、1和2 MPa下的裂缝扩展长度及方向，结果如表5所示。

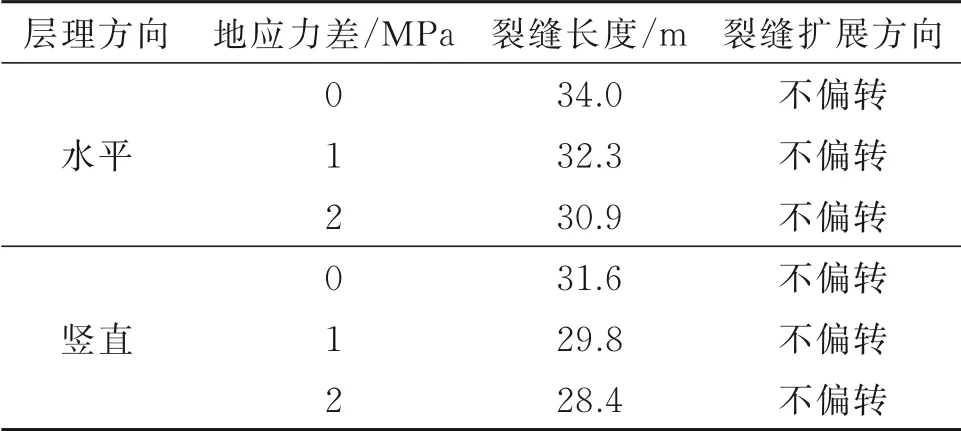
表5 含不同构造层理的裂缝扩展长度及方向Table 5 Length and direction of fracture propagation with different structural bedding

由上述结果可知：裂缝的扩展长度随着地应力差的增大而减小；当层理为水平构造方向，地应力差由0 MPa增加到1 MPa时，裂缝的扩展长度减小了1.7 m，减小的幅度为5%；当地应力差由1 MPa增加到2 MPa时，裂缝的扩展长度减小了1.4 m，减小的幅度为4.3%；当层理为竖直构造方向，地应力差由0 MPa增加到1 MPa时，裂缝的扩展长度减小了1.8 m，减小的幅度为5.7%；地应力差由1 MPa增加到2 MPa时，裂缝的扩展长度减小了1.4 m，减小的幅度为4.7%。

图14为含水平构造层理和竖直构造层理页岩注液点处的压力-时间及裂缝宽度-时间曲线，从中可以看出：（1）对于含水平构造层理的页岩，注液点处的压力和裂缝宽度随时间变化曲线在注液时间为50～75 s时，出现了较为明显的陡降段，该时间段正是裂缝扩展至水平层理并在其内扩展的阶段，这是由于层理的力学性质比页岩弱，在该段内裂缝更易扩展，造成裂缝宽度和扩展压力同时下降；（2）对于含竖直构造层理的页岩，由于初始裂缝布设在页岩上，裂缝在扩展过程中未发生偏转，因而并未穿过层理，故在曲线中未出现陡降段；（3）无论是含水平构造层理或是含竖直构造层理，注液点处的起裂压力和裂缝宽度均是随着地应力差的增加而增大，且裂缝长度越长，相应的注液点裂缝宽度则越短。上述结论与前文所述结论是一致的。

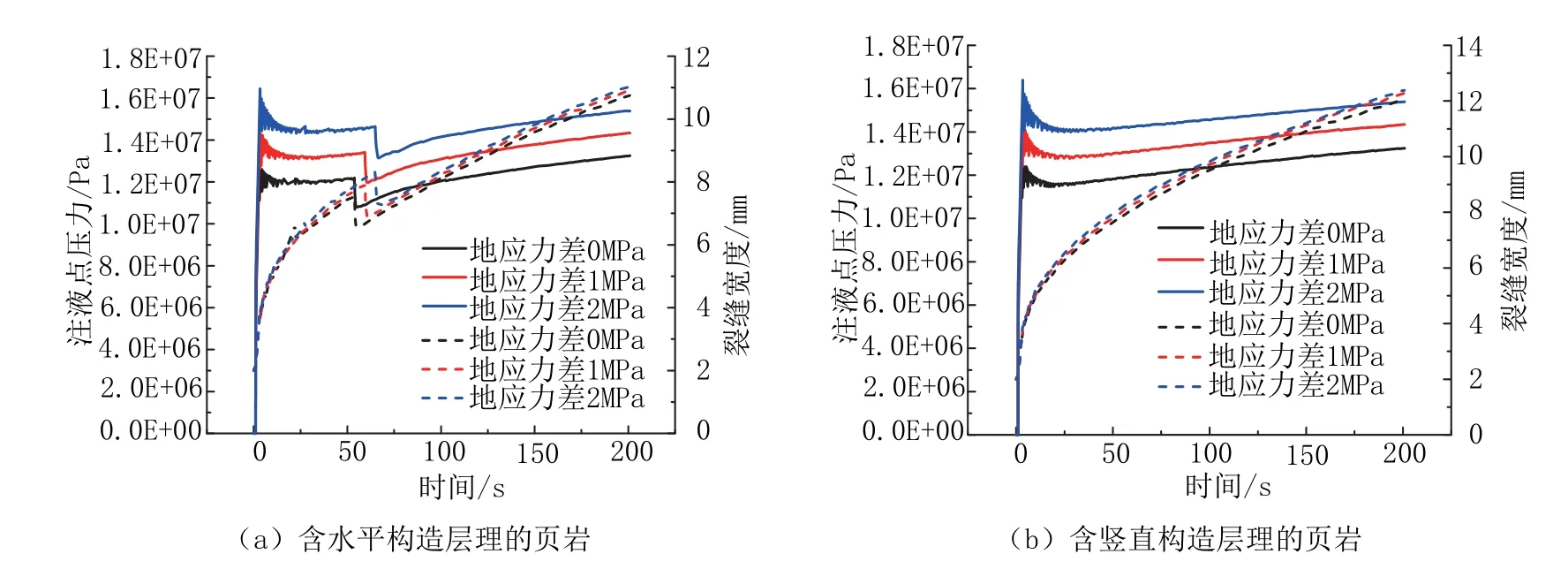
图14 含水平构造层理和竖直构造层理页岩注液点处的压力-时间及裂缝宽度-时间曲线Fig.14 Pressure vs time and fracture width vs time curves at the injection point in shale with the horizontal structural and the vertical structural bedding

3.2 层理内部倾角对裂缝扩展的影响

由于页岩是沉积岩，在其漫长的形成过程中除了可能会形成含不同构造层理的情况，层理内部物质也可能会由于褶皱、断层错动等地质构造原因产生一定的方向性。将层理内部物质与水平方向间的夹角称为“层理内部倾角”。在ABAQUS软件中可通过设置层理的材料方向实现对层理内部倾角的调整。前述研究都是基于层理内部倾角为0°所展开的。此处通过设置层理内部倾角分别为0°、30°、45°、60°和90°，地应力差均设为2 MPa，探究含水平构造层理和含竖直构造层理页岩中不同层理内部倾角下裂缝扩展的偏转情况。数值模拟的结果如图15、图16所示。

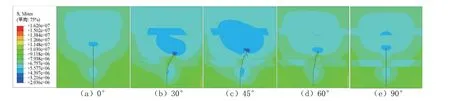
图15 含水平构造层理页岩中不同层理内部倾角下裂缝扩展云图Fig.15 Nephogram of fracture propagation in shale with the horizontal structural bedding under different bedding internal dip angles

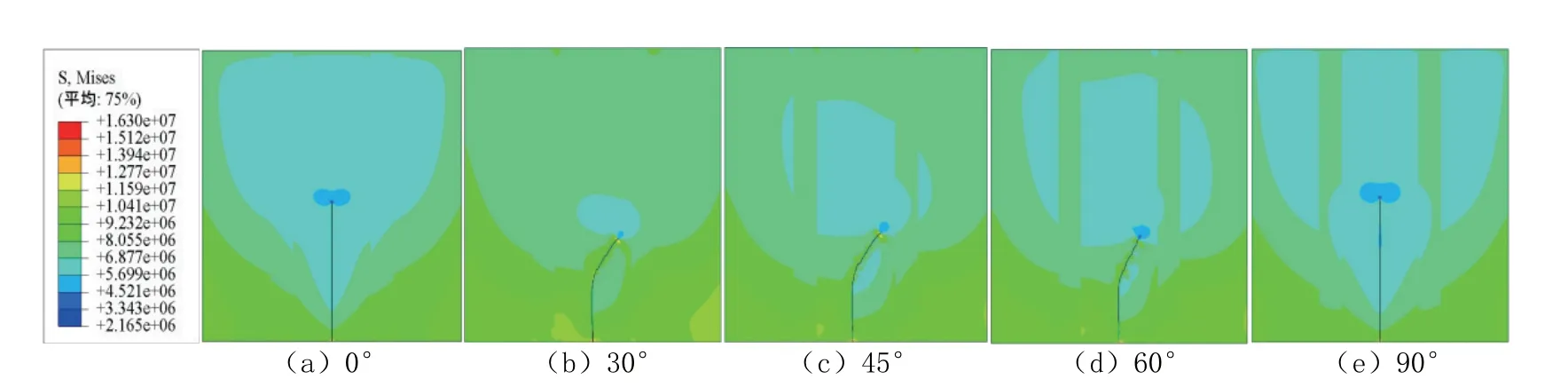
图16 含竖直构造层理页岩中不同层理内部倾角下裂缝扩展云图Fig.16 Nephogram of fracture propagation in shale with the vertical structural bedding under different bedding internal dip angles

由图15、图16可知：当层理内部倾角为30°、45°和60°时，裂缝的扩展都是先沿原方向扩展一段距离，而后再向层理内部倾角方向发生不同程度的偏转。此处以“裂缝扩展偏移比”表征裂缝扩展的偏转程度，它是指以裂缝扩展开始发生偏转时为起点，到裂缝扩展结束为止的这段裂缝的水平扩展长度与垂直扩展长度之比，结果如表6所示，从中可以看出对于含水平和竖直构造层理的页岩，当层理内部倾角为0°和90°时的裂缝不偏转，而当层理内部倾角为30°时的裂缝扩展偏移比最大，45°次之，60°最小，表明裂缝扩展的偏转程度随着层理内部倾角的增大而减小。

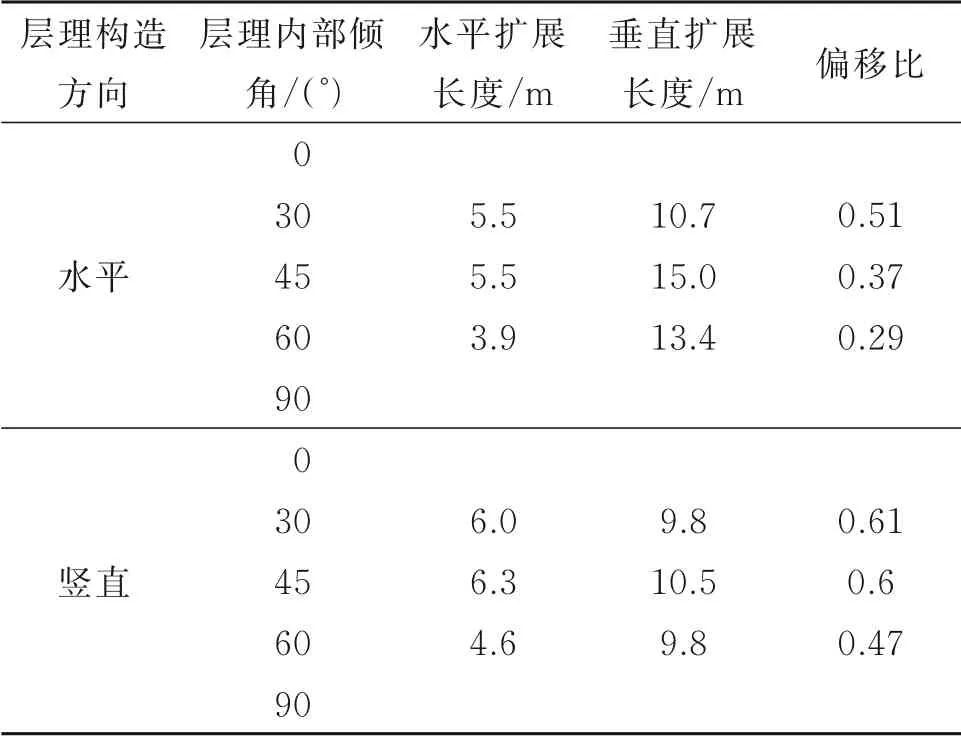
表6 不同层理内部倾角下的裂缝扩展偏移比Table 6 Fracture propagation deflection ratio under the different bedding internal dip angles

4 不同岩性层理对裂缝扩展的影响

在ABAQUS软件中建立如图1（b）所示的含45°方向构造层理页岩模型，且层理内部倾角为0°，探究分别为泥岩、煤岩和砂岩3种不同岩性层理时对裂缝扩展的影响。不同岩性的主要力学参数如表7所示，各工况的数值模拟结果如图17～19所示。

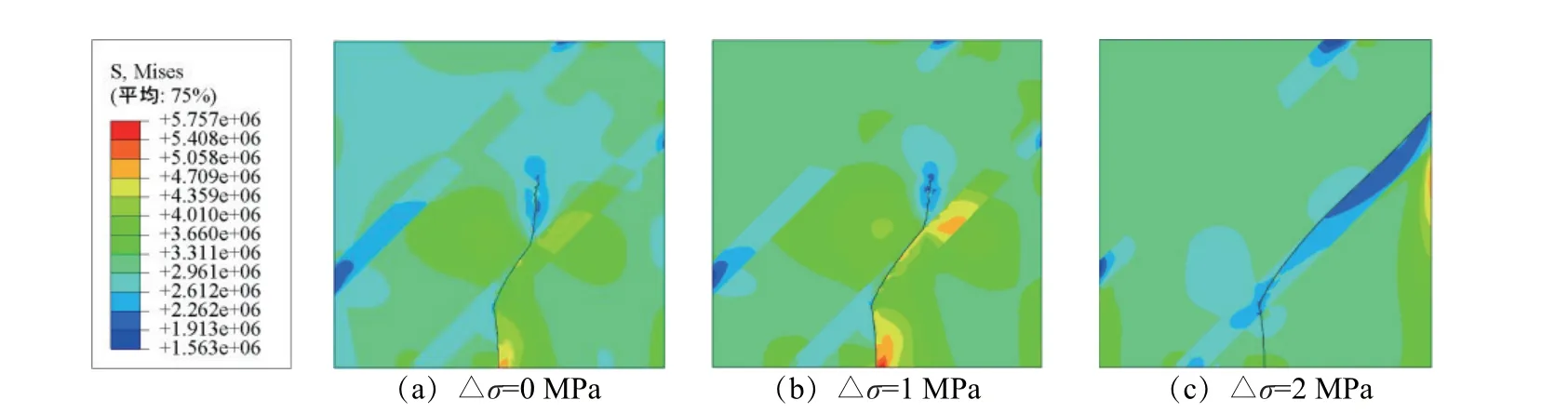
图17 工况一下裂缝扩展云图Fig.17 Nephogram of fracture propagation under working condition 1

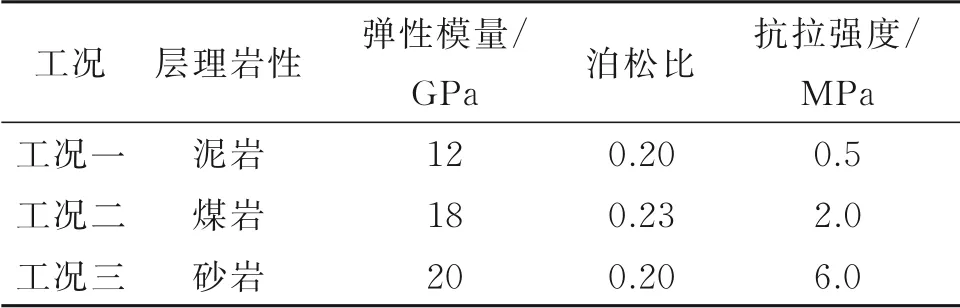
表7 不同岩性的主要力学参数Table 7 Main mechanical parameters of various rocks

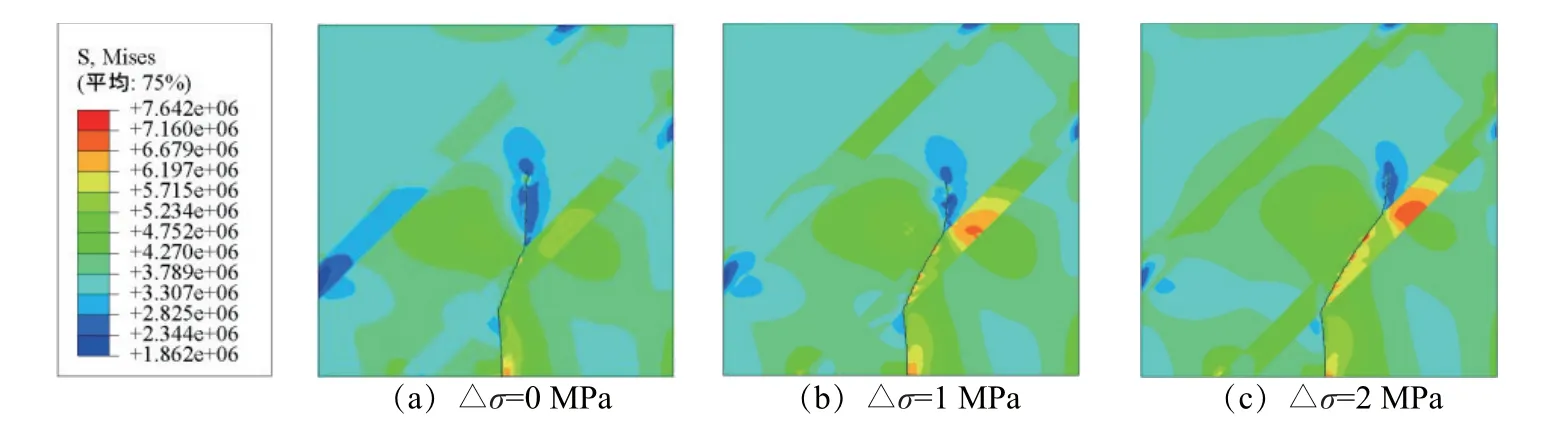
图18 工况二下裂缝扩展云图Fig.18 Nephogram of fracture propagation under working condition 2

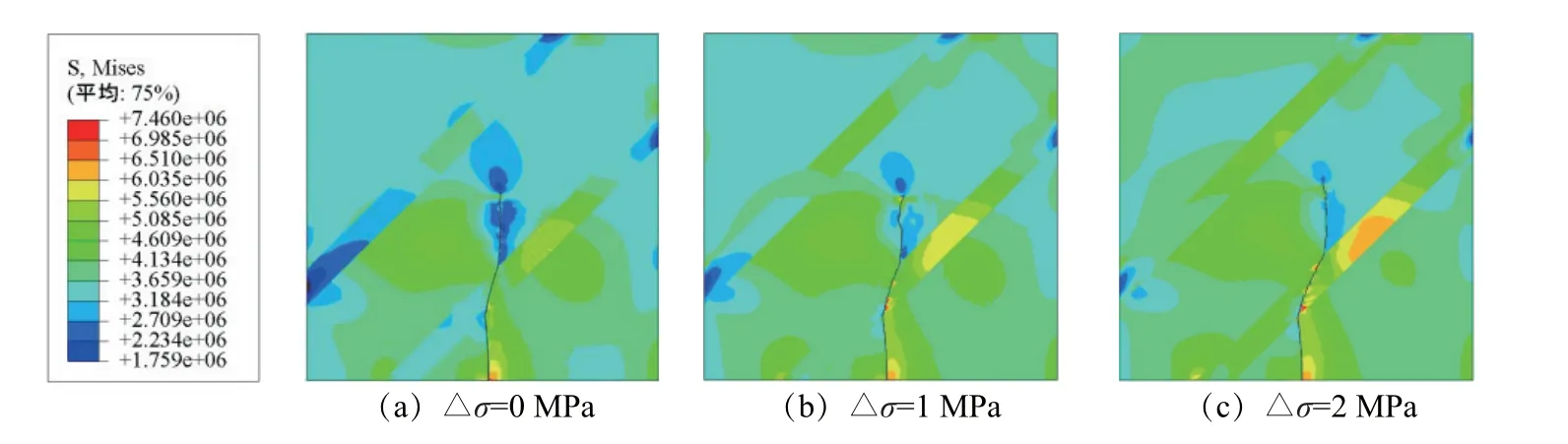
图19 工况三下裂缝扩展云图Fig.19 Nephogram of fracture propagation under working condition 3

由图17～19可知：（1）在3种不同工况下，当裂缝扩展至层理时均发生了偏转，但偏转的程度有所不同；（2）当层理岩性相同时，若地应力差不同，则裂缝在层理内的扩展规律也有较为明显的区别。为探究3种工况下裂缝在层理内的扩展情况，统计裂缝在层理内部的水平扩展长度和垂直扩展长度，结果如表8所示。

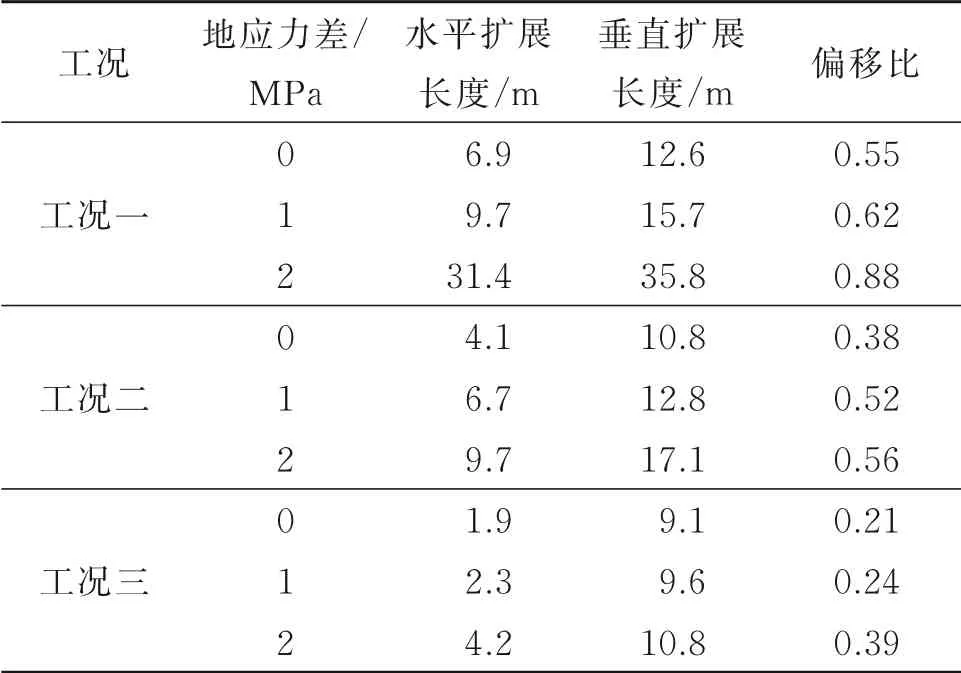
表8 各工况下裂缝在层理内的扩展情况Table 8 Fracture propagation in bedding under the various working conditions

由表8可知：（1）在工况一中的层理为泥岩时，由于其强度较小，故裂缝更容易在其内部扩展，且随着地应力差的增大，裂缝在层理内部扩展得更长，当地应力差为2 MPa时更是沿着层理向右侧贯穿了整个页岩模型，相应的偏移比为0.88；（2）在工况二和工况三中的层理分别为煤岩和砂岩，裂缝的偏移比仍是随着地应力差的增大而增大，但它们的偏移比均比工况一时的小；（3）在工况三中的层理为砂岩，这是所选3种材料中力学参数最大的一种，裂缝在砂岩层理中的偏移程度最小，当地应力差为0 MPa时的偏移比仅为0.21；（4）裂缝在层理为砂岩时的偏移程度最小，煤岩次之，裂缝在泥岩层理中更容易沿着层理扩展，其偏移程度最大；（5）对比各工况在不同地应力差下的偏移比，可知随着地应力差的增大会加剧裂缝在层理内部的扩展，从而造成偏移比增大，则裂缝偏转得更为明显。

5 结论

通过运用大型有限元软件ABAQUS中的扩展有限元模块对不同页岩模型水力压裂裂缝的扩展规律进行数值模拟研究，可得出以下结论：

（1）对于均质页岩模型的水力压裂裂缝扩展，当裂缝沿着垂向扩展时，随着水平主应力的增大裂缝更难扩展，表现为裂缝的扩展长度更短、起裂压力更大；当裂缝向两端同时扩展时优于裂缝仅向一端扩展的情况；当初始裂缝处于页岩中部且呈45°方向时，裂缝的扩展会向着最大水平主应力方向发生偏转，且裂缝的偏转程度随着最大水平主应力的增大而增大；水力裂缝扩展得越长，则其注液点处的裂缝宽度越小；对于水力裂缝不偏转时，距离注液点越远处的裂缝宽度越小，若水力裂缝发生偏转，则未必有这种趋势；对于分时多簇压裂，先形成的裂缝会影响后续新裂缝使其朝远离该裂缝方向扩展，且会影响裂缝扩展的形态和裂缝的起裂压力，对比首次起裂，后续裂缝的起裂压力会相对增大，对各个注液点的裂缝宽度影响又相对较小。

（2）对于含水平和竖直方向构造层理的页岩，当水力裂缝扩展至层理时，其注液点处的裂缝宽度和扩展压力会迅速下降；对于不偏转的水力裂缝，地应力差对均质页岩的影响规律与含水平和竖直构造层理页岩的影响规律一致；改变层理内部倾角，水力裂缝会出现不同程度的偏转（0°和90°除外），且水力裂缝的偏转程度随着层理内部倾角的增大而减小。

（3）对于含45°方向构造层理的页岩，水力裂缝在层理为砂岩时的偏移程度最小，煤岩次之，泥岩最大，表明当层理的力学参数越弱时，裂缝越容易在其内部扩展，且裂缝的偏移程度会随着最大水平主应力的增大而增大。

（4）本文重点探究了不同地应力差的工况下均质页岩中初始裂缝的位置、方位角、数量，以及含层理页岩层理的构造方向、内部倾角及岩性对水力裂缝扩展的影响，但在页岩气水力压裂实践中，压裂液排量、粘度等压裂工艺参数对裂缝扩展也有较大影响，这些将在后续研究中加以综合考虑。