基于GA的BP网络算法优化及应用
林浩宇
(福州大学 物理与信息工程学院,福建 福州 350000)
0 引 言
BP(Back Propagation,BP)神经网络在生活中的应用处处可见,如数字识别系统的设计、PID参数的整定值、函数逼近以及模式识别的应用,都可以基于BP神经网络展开[1]。BP算法具有精确性高等优点,但是也存在收敛速度慢、易陷入局部极小问题的缺点[2]。遗传算法(Genetic Algorithm,GA)作为生物智能算法的一种,基于生物进化理论基础发展而来,是一种自适应性的算法,能够对一个数据空间进行全局部优,而且在收敛性方面也有一定的优越性[3]。本文将遗传算法与BP神经网络算法巧妙地结合在一起,利用遗传算法对BP神经网络进行权值与阈值求解,并进行优化处理,从而得到权值和阈值的最优解,使BP神经网络结构的稳定性大幅度提升[4-5]。
在理论研究方面,朱苗苗等人将BP神经网络和遗传算法结合形成一种交互式算法[1];在日常的生活应用中,徐星等人基于遗传算法优化的BP网络对矿井的水质进行了分析[6];在对未来数据走势预测领域,谢梦蝶、秦江涛通过遗传算法优化的BP神经网络实现了对股指进行预测及研究[7];谢文强通过遗传算法优化的BP网络对锂离子电池剩余容量进行预测[8]。这些涉及日常生活各个领域的实验及实践有力地证明了遗传算法优化的BP网络具有很强的实用性,也展现了遗传算法的高效性与可利用性。
在数据云集的时代,BP神经网络在生活中的应用处处可见。它可以对事物的未来变化过程进行预判,从而成为趋势预测领域的有力工具之一。它利用构建相对应的模型,通过过去产生的数据随时间推移变化的规律,对数据未来的趋势进行预测[9]。但是,传统BP神经网络存在收敛速度慢等缺点,有一定的局限性,而遗传算法优化的BP神经网络,能很好地弥补传统BP神经网络的这一缺点。优化后的BP神经网络具有适应性强、网络稳定度高的优势。
1 遗传算法理论
遗传算法GA是一种生物智能优化算法。它实质上是一种全局搜索寻找最优值的技术。遗传算法针对对随机产生的可能结果,在这些结果中选择一定量的可能解作为一个种群,根据相应的规则,即自然遗传学的选择及交叉变异等方法,通过种群的迭代,得到最优解。在种群迭代的过程中,需要对个体适应度的大小进行比较,按照优胜劣汰以及适者生存的原理,逐渐搜索得到一个最优解,最终得到一个新的解集的群体。这个解集即需要解决的问题的最理想的解[10-11]。
遗传算法解决实际问题的步骤如下[12],流程如图1所示。
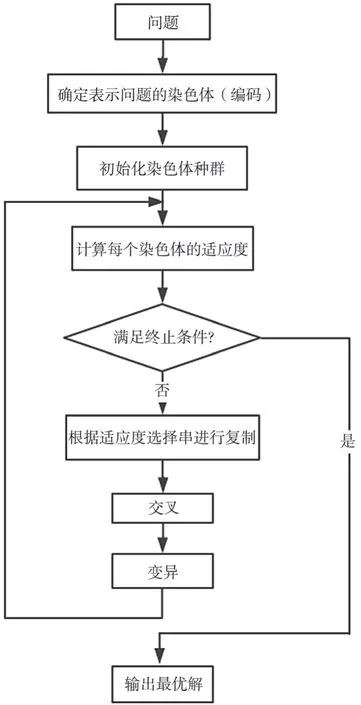
图1 遗传算法流程图
(1)初始化。通过遗传算法参数编码在N个样本中随机选择,确定一个初始种群P(0),形成一个可行解的集合。
(2)个体评估。把初始的种群P(0)导入目标函数,然后算出样本中各种群的适应度。
(3)结束条件判断。给定一个初始条件,判断算法结束条件,如满足条件直接跳到至步骤(8)。
(4)选择运算。对目标群体采用优胜劣汰、适者生存的法则,选择出大量优良个体。
(5)变异运算。通过变异概率对目标个体进行变异运算。
(6)交叉运算。通过交叉概率对目标个体进行交叉运算。
(7)经过变异、交叉随机运算,如果得到由N个新个体构成的下一个群体P(t+1)转至步骤(2),反之转至步骤(4)。
(8)进化个体。得到函数中适应度最高的一个个体,这个个体即该问题的最理想的解,结束运算。
2 遗传算法优化的BP网络
BP神经网络虽然操作简单、实用性强,在数据预测和图像分割领域有很大优势,但也难免存在一些问题,如收敛速度慢、算法稳定性较差、容易落入局部极小值等。而遗传算法在全局搜索方面表现出色,通过遗传算法得到BP神经网络权值和阈值优化求解,就可以得到稳定的网络结构,在图像分割处理、数据计算以及趋势预测方面都有较好的完善和改进,是值得一做的优化方案。
为了充分发挥遗传算法和BP神经网络两者的优势,本文通过遗传算法对BP神经网络进行改进优化,优势互补。具体步骤如下[13-14],流程如图2所示。

图2 遗传算法优化的BP网络流程图
(1)初始化:对整个种群进行初始化处理,利用参数编码生成N个个体,这N个个体形成新的初始种群,然后对种群数进行计算,确定染色体长度和范围,给出理想的误差值。
(2)适应度计算:计算出适应度f,公式如下。

式中:yi为网络期望的输出,oi为实际的输出值,SE为误差平方和函数。
(3)交叉运算:步骤(2)计算出适应度f,通过优胜劣汰的原则,筛选出优良个体,对其进行交叉运算。即选择第k个染色体ak和第i个染色体ai,在第j位的交叉运算方式如下。

式中:b∈[0,1]。
(4)变异运算,第i个个体在第j个基因进行变异运算公式如下。

式中:amax和amin分别为染色体aij的上下界,f(g)=r(1-g/Gmax);g为进行到当前的迭代次数,Gmax为进化的最多次数,r∈[0,1]。
(5)评估:对种群中个体的适应度进行计算并计算误差。
(6)判断是否满足终止的条件,如果满足,转至步骤(7),反之转至步骤(3)。
(7)得到BP网络最优的权值和阈值。
(8)对BP网络进行校正,调整各层参数。
(9)计算BP网络的误差,如果误差在要求的范围内,则结束整个过程。反之转至步骤(7),继续校正网络参数。
(10)得到优化后的数据,对网络空间和映射关系进行保存。
3 实验与性能
为了验证该优化的网络的实用性,以矿井通风量为研究对象Data0,通过总回风巷的通风量、瓦斯、煤尘、温度和湿度等数据对最优矿井通风量进行计算。需要注意的是,总回风巷的气流量等于回风巷和掘进工作面气流量之和,具体数据如表1所示。
根据表1的数据,绘制出各因素对应下的通风量之间的三位曲面图,如图3至图8所示。

表1 某总回风巷的数据点
由图3至图8可以看出,不同变量对通风量影响是不同的,可能由工程中间间断作业造成。采用GA-BP网络对通风量最优值进行预测,经过初始化、适应性函数、选择、交叉、变异等操作后,得到相关的适应度曲线,最后输出优化过后神经网络的预测值及误差值,如图9至图11所示。
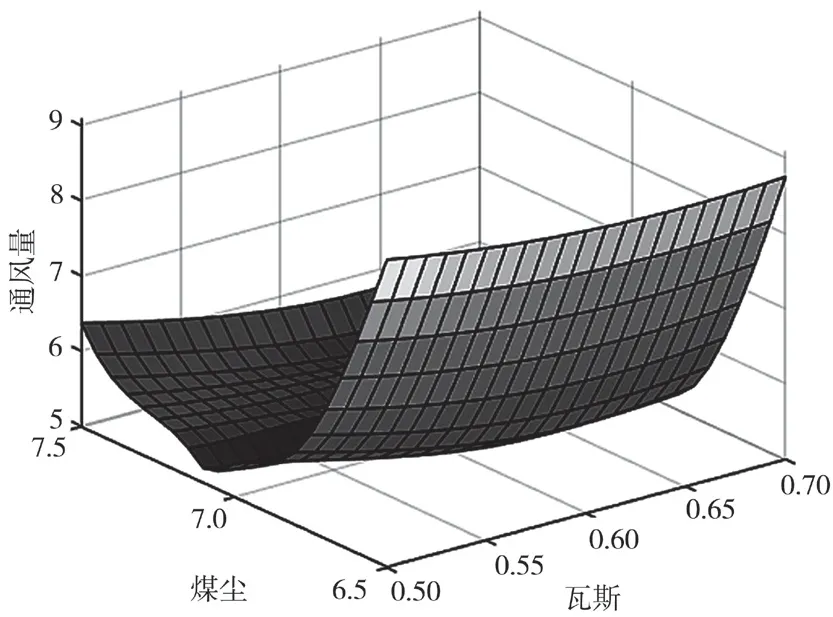
图3 某总回风巷煤尘、瓦斯与通风量之间的关系图
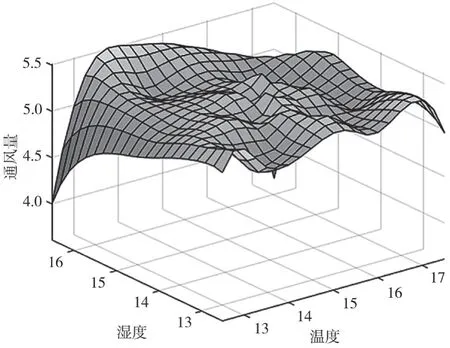
图8 某总回风巷湿度、温度与通风量之间的关系图
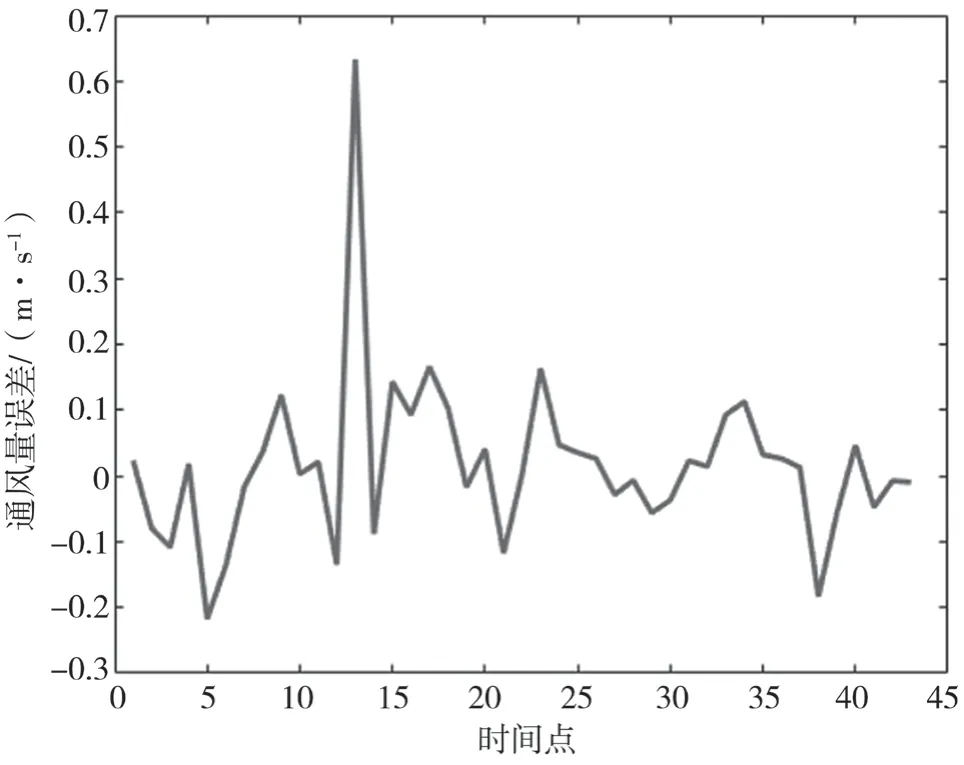
图9 总回风巷预测误差分析

图4 某总回风巷湿度、瓦斯与通风量之间的关系图
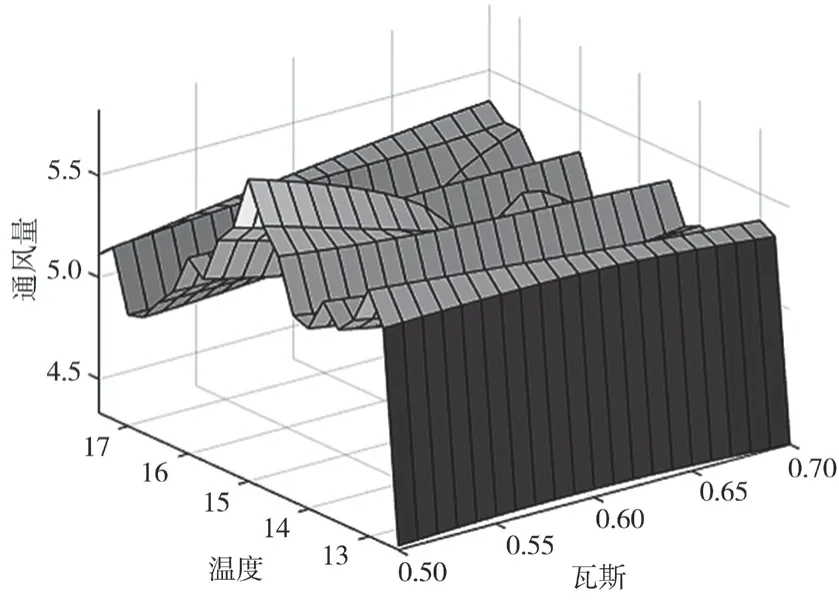
图5 某总回风巷温度、瓦斯与通风量之间的关系图

图6 某总回风巷温度、煤尘与通风量之间的关系图

图7 某总回风巷湿度、煤尘与通风量之间的关系图
根据图11,得出GA-BP预测与回归总回风巷预测的误差比较如表2所示。

图10 总回风巷最优通风量预测

图11 GA-BP预测与回归预测总回风巷误差比较
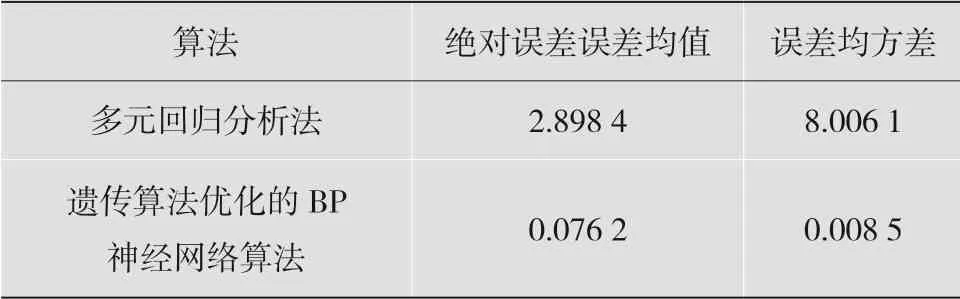
表2 GA-BP预测与回归总回风巷预测的误差比较表
由图9至11可以得知,GA-BP网络系统进行全域搜索,得到通风量的最优条件是:瓦斯0.5%,煤尘6.5 g·m-3,温度16.5 ℃,湿度12.5%RH,预测的最优风速为4.158 4 m·s-1。由此可以得出,所得到的预测结果相较于回归分析法误差更小,预测结果更平滑,数值更精确,在一定程度上具有一定的鲁棒性和泛化能力。
4 结 语
本文的实验充分证明了遗传算法优化BP神经网络的可行性,即利用遗传算法极其强大的全域搜索能力,确定BP神经网络的最优权值和阈值,使计算预测性能大幅度提升。实验得出的结论也很好地印证了提出这一改进算法的初衷,即要求在误差可控制的范围内提高BP网络算法的稳定性。
作为研究者,要清楚地认识到,遗传算法与BP网络结合只是一个进步的开端。接下来,研究者还需要去做多次实验来进一步提高该算法的稳定性和实际操作性,需要不断降低预测误差。既然这个优化算法在初步试验中被证明其具有可行性,应该将这种思维应用到更多算法中,更高效、更稳定地实现数据预测的优化。

