基于TwIST的UWB精确定位算法设计及仿真

杨 柳，袁光福，赵 涛，郭子文*，吴 坚

（1.95875部队，甘肃 酒泉 735000；2.95859部队，甘肃 酒泉 735000；3.航天新通科技有限公司，重庆 401332）

0 引 言

位置信息作为一个时空基础，在万物互联的时代，发挥着不可替代的作用。在当今社会，位置信息不仅关系着国家的安全，也关系着国民经济的发展。在测控方面，在一些卫星定位无法使用的情况，如卫星定位受干扰的情况下，急需其他定位技术的补充。此外，如智能制造、车联网等一些国家重点发展的战略方向领域，都需要精确的位置信息。

室外定位环境中，全球导航卫星系统（Global Navigation Satellite System，GNSS）可以在开阔地带提供良好的定位精度，一般情况下可以达到数十米级的定位精度，如果使用实时动态测量（Real Time Kinematic，RTK）的方式进行定位，可以达到厘米级的定位精度[1]。但GNSS信号在遇到阻挡时会快速衰减，同时也会产生多路径效应，降低接收信号的质量，不利于解算出距离信息，导致定位精度受到影响，因此GNSS在如仓储工厂、智能制造、地下停车场等室内环境难以进行精确定位。

超宽带（Ultra Wide Band，UWB）无线电定位、蓝牙定位、蜂窝定位、ZigBee定位、WiFi定位、无线射频标签（Radio Frequency Identification，RFID）定位、地磁定位、伪卫星定位、计算机视觉定位、可见光定位、红外定位以及超声波定位等[2-6]是较为常见的几种室内定位方式。其中，UWB定位技术不采用传统的载波调制解调方式，而采用ns级的脉冲窄带信号来直接传输UWB信号[7]，频带范围可达到3.1～10.6 GHz，在噪声较大的环境中同样可以正常工作。此外，UWB脉冲的功率谱密度很低，能够有很好的时间分辨率，同时又有很强的抵抗多路径干扰的能力。UWB定位系统的主要优势集中在定位精度、功耗、抗噪声及穿透性能力等方面。

根据测距观测量的不同，定位算法主要分为基于时间定位的到达时间法（Time of Arrival，TOA）、到达时间差法（Time Difference of Arrival，TDOA）、基于信号角度的定位方法（Angle of Arrival，AoA）以及基于信号接收强度的定位方法（Received Signal Strength Indication，RSSI）[8-11]。其 中，TDOA算法不需要得到绝对时间，时间同步的要求更低，系统复杂度更小，是目前主流定位系统使用的算法之一。

在使用TDOA算法进行目标的位置求解过程中，需要对得到的定位方程组进行求解。Chan算法[12]采用二重最小二乘法对该方程组进行求解，在TDOA测量误差较小时，具有最优的估计性能。本文提出了一种基于两步收缩阈值（Two-step Iterative Shrinkage Thresholding，TwIST）[13]的定位方案，详细分析对比了基于TwIST算法和基于Chan算法求解目标位置的性能，并采用Kalman滤波算法对数据进行了滤波处理，分别应用到这两种算法中，通过仿真分析，验证了基于TwIST的TDOA定位算法的有效性，提高了定位的精确度。

1 定位原理

1.1 TDOA定位

到达时间差法（TDOA）是通过测量信号的到达时间，而后使用到达时间之差进行定位计算。移动台坐标位置为通过达到时间差构建的双曲线交点。TDOA原理如图1所示。

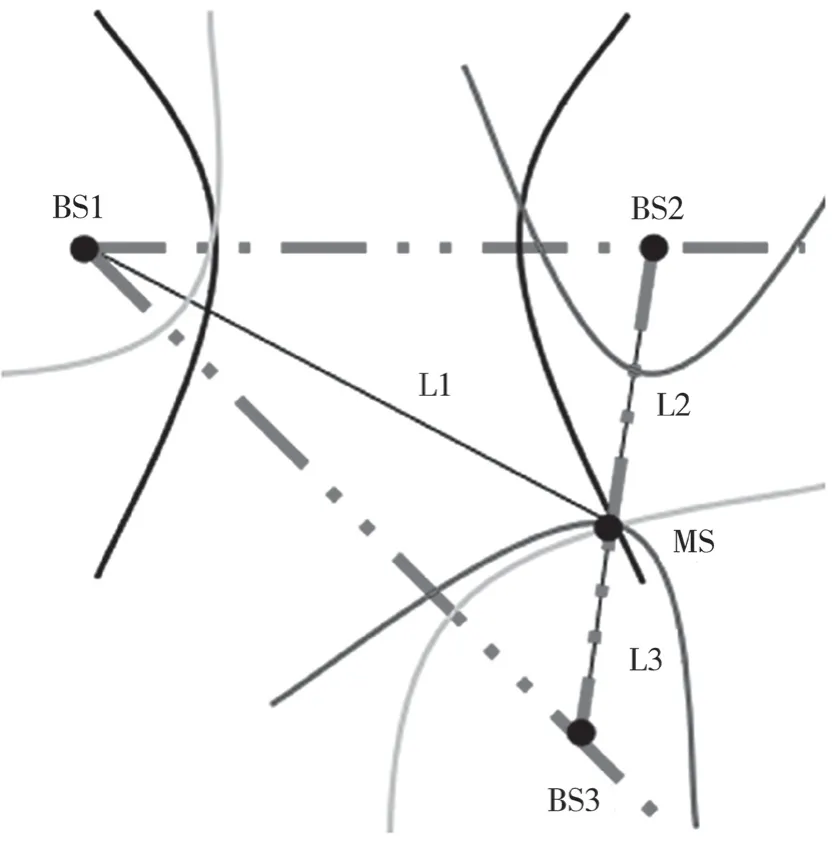
图1 TDOA原理图

图1中，BS1，BS2，BS3为UWB基站位置，MS为标签位置，测得基站BS1、BS2、BS3到标签MS的距离分别为L1，L2，L3。在实际的UWB定位系统中，通过对达到时间的测量，使用时间与距离的换算公式Δdij=c(Δti-Δtj)可以计算出未知位置的移动台与两个己知坐标位置的测距基站的距离之差，再根据这个距离差和己知基站的坐标，可以得到多条双曲线。而移动台的理论坐标位置就位于这些双曲线的公共交点上。当出现n个不在一条直线上的基站时，就可以得到n-1个双曲线方程，这些双曲线的交点即为移动台的坐标位置。根据TDOA定位模型，通过求解下述方程组，最终可以得到移动台的位置。

1.2 Two-Step IST（TwIST）算法

Bioucas D J M和FIGUEREDO M A在文献[13]中提出了一种两步迭代阈值收缩算法（TwIST）。该算法同时具有IST算法[14]良好的去噪性能以及IRS算法高效处理病态问题的优点。TwIST算法的核心思想是利用前两个迭代值去更新当前值，也就是所谓的“两步”迭代收缩算法。令C=I+λDt，R=I-KtK，借助两步固定迭代算法思想A=C-R，则有A=λDt+KtK，求线性方程组Ax=b可以转变为：

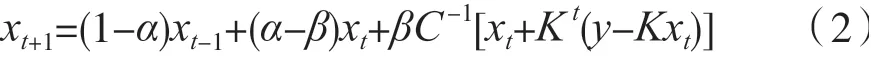
将 式（2）中 的C-1用 去 噪 算 子ψλ()代 替，TwIST算法的迭代格式如下：

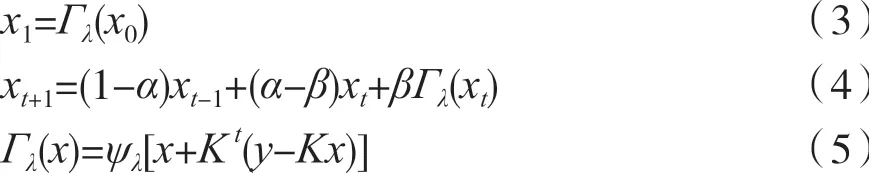
式中：α和β为TwIST中定义的参数，0≤α≤1，0＜β＜2α，实验中，α和β在较大范围内均可保证解算结果收敛；ψλ是基于正则化的去噪算子。从式（3）～式（5）可知，下一次的迭代结果xt+1不仅依赖于当前的结果xt，也将考虑上一次的结果xt-1，也就是需要前两步的迭代结果。关于TwIST算法的收敛性能以及参数α和β的计算方式等详细推导过程请参考文献[13]。

1.3 卡尔曼滤波

数据滤波通过去除噪声来还原真实数据。卡尔曼滤波（Kalman）是一种数据滤波方式。Kalman滤波在测量方差已知的情况下，能够从一系列存在测量噪声的数据中，估计动态系统的状态。Kalman滤波是目前应用最为广泛的滤波方法，便于编程实现，并可做自适应的实时参数更新，广泛地应用于通信、导航与控制等多个领域。

卡尔曼滤波利用系统模型和观测模型的统计特性，通过递推得到最优的数据。通过使用先验估计值和观测值进行加权计算的思路进行优化，即：当前状态的估计值=基于上一时刻的预估值+当前状态观测值。

假设某一随机线性离散系统的状态向量Xk，系统过程随机噪声Wk，系统状态转移矩阵Φk,k-1，噪声输入矩阵Γk,k-1，系统观测值Zk，观测矩阵Hk，观测噪声Vk，则状态方程和观测方程为

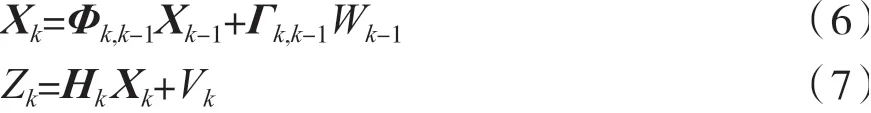
系统过程噪声方差Qk正定，观测噪声方差Rk非负定，Kk卡尔曼滤波估计过程如下。

状态一步预测：

状态估计：

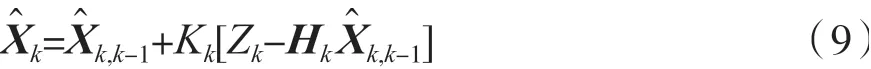
滤波增益矩阵：

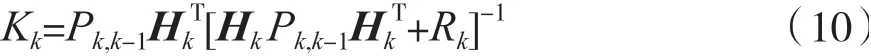
一步预测误差方差阵：

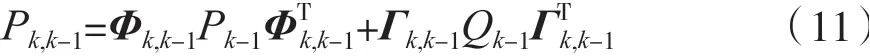
估计误差方差阵：

式中：为k时刻的状态估计值，Pk为k时刻的估计误差方差。通过系统的初始值X0和P0，根据在第k时刻的观测值Zk，通过递推的方式推断出第k时刻的状态估计值(k=1,2,3,…)。

2 仿真与实验分析

2.1 基于TwIST的定位算法设计

基于TwIST的定位算法主要为求解通过TDOA算法得到的线性方程组Ax=b，不同于Chan算法中使用改进的最小二乘进行方程组的求解。为获得更高的去噪性能和更快的收敛速度，本文提出的算法使用了两步收缩阈值的方式进行方程组的求解。定位算法主要流程如图2所示。

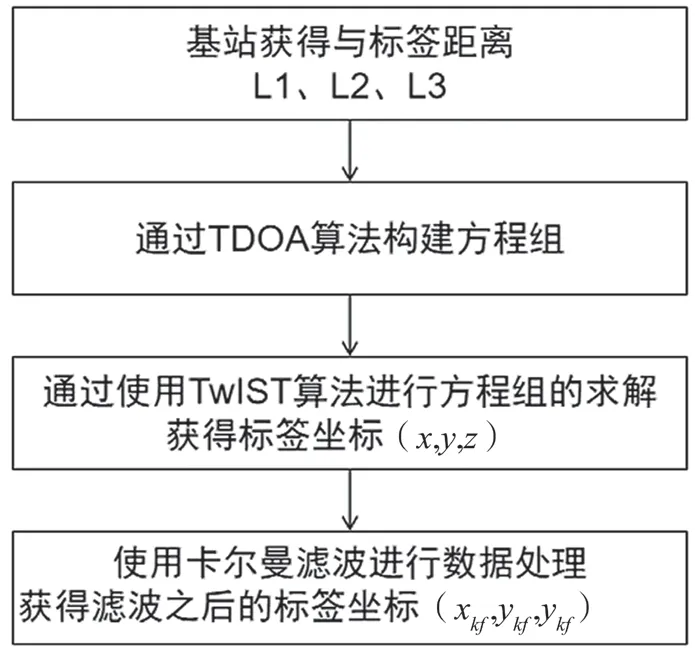
图2 基于TwIST的定位算法框图

基于Chan的TDOA定位算法在求解方程组的过程中则是先将初始非线性TDOA方程组转换为线性方程组，然后采用最小二乘法得到初始解，再利用第一次得到的结果及已知约束条件进行第二次最小二乘估计，从而得到标签坐标。

2.2 基于仿真模型的定位解算

本文首先使用MATLAB软件建立一个静态标签定位仿真模型，建立了一个基站数量为6的定位小区。基站位置以及标签位置平面如图3所示。

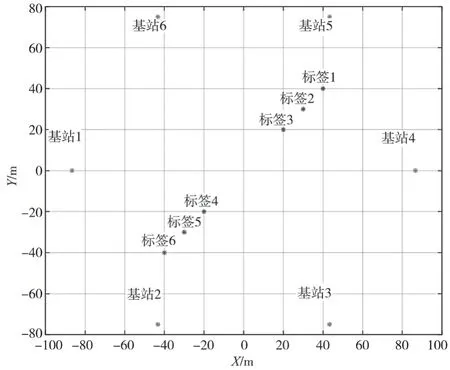
图3 仿真的基站与标签位置平面图

分别使用本文提出的基于TwIST的定位算法和基于Chan的TDOA定位算法进行位置坐标求解。在定位解算完成后，对定位结果进行卡尔曼滤波处理，得到均方根误差（Root Mean Square Error，RMSE）数值对比结果，如表1所示。

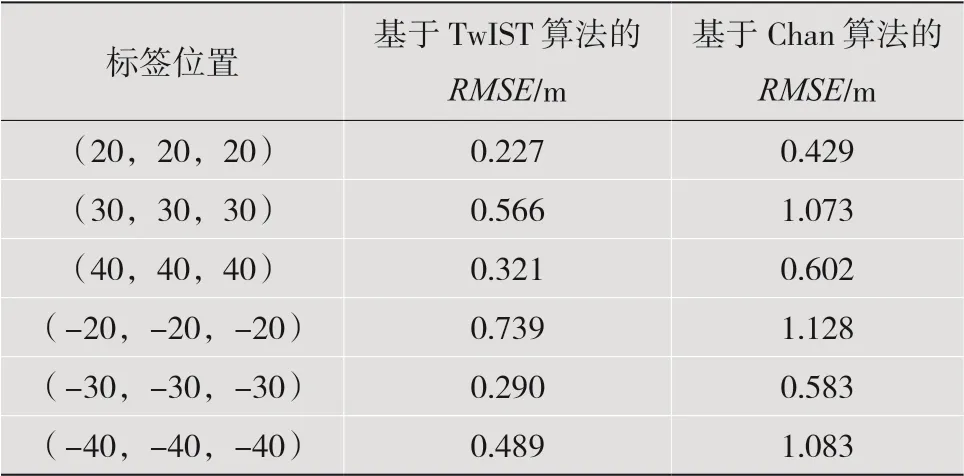
表1 均方根误差数值对比

从均方根误差RMSE结果可得，使用基于TwIST算法进行定位解算得到的位置结果比基于Chan的TDOA算法得到的结果精确度高50%。

2.3 基于实验数据的定位解算

在使用仿真模型得到的仿真数据进行定位解算、分析并对比使用基于TwIST的定位算法和基于Chan的TDOA定位算法的定位性能后，为进一步验证本文算法在UWB定位中有更优的定位精度，本文进行了定位实验测试，图4为实际的测试场景。

图4 实验测试场景

具体的基站位置以及标签位置如图5所示。

图5 实验的基站与标签位置图

基站位置分别为（0.0，0.0），（1.8，4.2），（0.0，8.4），（1.8，12.6）。在此次定位实验中，共测量收集到6组实验数据，分别为标签位置在（0.6，1.2），（0.6，2.4），（0.6，5.4），（0.6，7.8），（0.6，9.6）和（0.6，12.0）时所得到的距离数据。

分别使用本文提出的基于TwIST的定位算法和基于Chan的TDOA定位算法进行二维位置坐标求解，在定位解算完成后对定位结果进行卡尔曼滤波处理，得到均方根误差数值对比结果如表2所示。

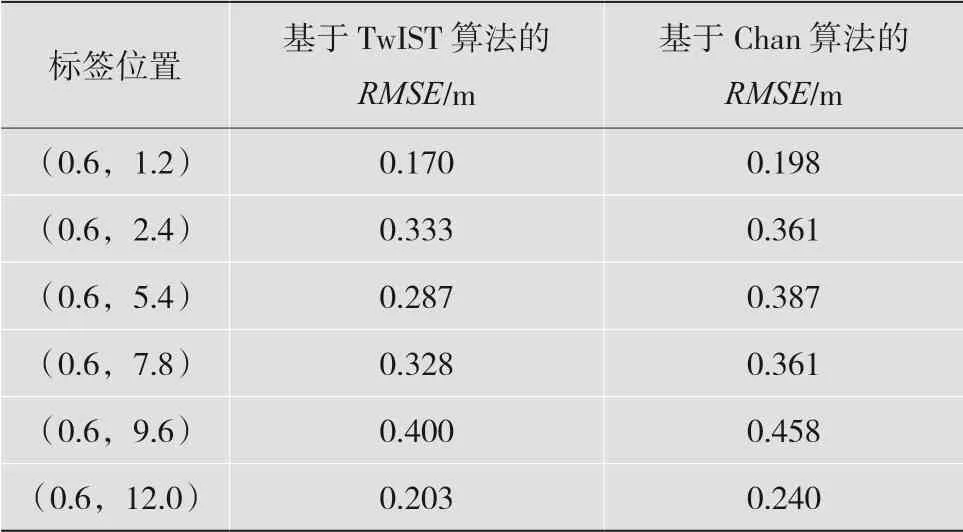
表2 均方根误差数值对比

在使用实验测量数据的条件下，分别使用本文提出的算法和基于Chan的TDOA算法进行二维的标签位置解算，从得到的均方根误差RMSE表格可以得出，基于TwIST的定位解算算法效果要优于基于Chan的TDOA算法，定位精度提高了约15%。

3 结 语

UWB定位作为当前精度最高的室内定位技术，在遥控遥测应用对位置信息有需求、无法使用卫星定位的情况下，可以作为辅助系统获取目标位置信息。本文设计了一种基于两步迭代阈值收缩法（TwIST）结合卡尔曼滤波的UWB精确定位算法，充分利用了TwIST算法去噪性能好、收敛速度快的优点。通过与基于Chan算法仿真和实验数据的定位结果对比发现，该算法提高了UWB系统的定位精度；同时，通过对比二维和三维的定位结果可得，本文提出的算法得到的位置信息在三维定位中的效果更好，具有更高的空间分辨率。