基于校准补偿和VBUKF平滑的超宽带采煤机定位技术

曹 波，王世博，葛世荣， 刘万里，马光明，梁 耍

(1.中国矿业大学 机电工程学院，江苏 徐州 221116；2.安徽科技学院 机械工程学院，安徽 蚌埠 233033)

0 引 言

煤矿智能开采是国内外煤炭开采领域共同追求的前沿技术[1-2]。采煤机是综采工作面的核心设备，要实现智能化开采必须实现采煤机智能化，监测采煤机在工作面的位置是实现智能化、无人化开采的关键。针对采煤机的定位技术主要有：红外线定位[3-4]、无线传感网定位[5-6]、里程计定位[7-8]、激光定位[9]、超声波定位[10]、惯性导航定位[11-13]。其中惯性导航定位技术广泛应用于采煤机定位，已得到煤机企业和煤矿普遍认可[14]。但是惯性测量元件随着时间和距离的推移存在漂移现象，导致定位误差不断累积增加，定位精度逐渐下降，无法满足定位要求。因此需要其他定位技术辅助惯性导航定位，当采煤机即将运行到端头时，为惯性导航提供采煤机的位置信息。

UWB(Ultra-Wideband，超宽带无线通信技术)具有抗干扰能力强、测距精度高、抗多径及穿透性强等优点[15]，已经被应用于采煤机定位，刘清[16]和王雪松[17]等提出基于超宽带测距原理的采煤机定位系统，并在井下进行了测试。樊启高[18]提出采用自适应模糊卡尔曼滤波技术进行INS/UWB组合导航数据融合的方法提升定位精度；方文浩[19]提出基于区域判定的方法提高测距精度，采用三角形质心算法进一步提高定位精度。刘一鸣[20]提出了利用信息过滤算法对UWB定位结果进行过滤，利用神经网络算法对刮板输送机机头位置每个时间段的数据进行评估，提高采煤机定位精度，但是忽略了NLOS环境的存在；刘万里[21]提出一种基于UWB采煤机绝对位置精确校准的方法，将UWB布置均匀布置在巷道中，由于NLOS的影响，定位精度较低。为减小NLOS误差的影响，提高定位精度，田野[22]利用UWB测距建立采煤机误差预测模型，提高NLOS下采煤机定位精度。笔者[23]采用高斯混合模型对测距值进行平滑处理，然后利用交互式多模型滤波分别对视距环境(LOS)测量值和NLOS测量值进行滤波，获得精度较高的测距值，采用扩展卡尔曼滤波进行定位，可获得较高的定位精度。孙继平[24]采用卡尔曼滤波消除突发非视距(NLOS)对测量数据的影响，在此基础上提出基于历史和卡尔曼阈值的最近邻居指纹定位方法，提高矿井定位的精度，但定位误差仍然较大，平均定位误差在1.4 m左右。李旭红[25]针对井下NLOS环境下的定位精度不高的问题，提出以联合定位得到的初始坐标作为无迹卡尔曼滤波(UKF)算法的观测值，并对UKF的测量更新方程进行修正，但在实际工况中，系统的测量噪声随着时间动态变化，使得的滤波性效果不佳。

通常情况下，假定基站的位置坐标是非常准确的，但是在实际的作业环境中，基站在安装过程和位置坐标确定时，不可避免存在位置误差。影响UWB系统定位精度的主要因素是视距误差、非视距误差及系统自身的误差，很多研究者容易忽略基站的位置误差对定位精度的影响。基站的位置误差也是引起定位精度较低的原因之一。尽管上述研究者对消除非视距误差进行了研究，但是均未考虑到基站位置误差对定位精度的影响。尤其是在复杂的环境下，基站的位置坐标很难准确的测量，即使获得高精度的测距值，也很难得到较高的定位精度。

针对上述问题，提出一种校准方法，在LOS环境下，通过定位区域中的参考节点与基站进行测距，对基站位置误差、尺度因子误差和偏差进行补偿，达到校准的目的；针对NLOS环境，考虑到测量噪声时变性，提出采用变分贝叶斯无迹卡尔曼滤波(VBUKF)对测距值进行平滑，减小非视距误差的影响；经过校准和VBUKF平滑处理后，采用Caffery定位算法(CL)求解目标节点的坐标，为进一步提升定位精度，采用高斯-牛顿迭代算法(GN)对CL算法的结果进行优化。

1 UWB定位系统

为获得采煤机的三维坐标，有研究者提出将UWB基站安装在液压支架顶端和底端[2,16,18]，将目标模块安装在采煤机机身上，通过UWB自组网的形式获得目标模块与对应基站之间的距离，采用相关的定位算法解算采煤机的位置坐标。但是液压支架的频繁移动，导致基站的位置坐标不断发生改变，很难准确确定移动后基站的坐标，进而导致采煤机的定位精度较低。基于此，笔者提出将UWB基站安装在综采工作面端头位置，如图1所示，当采煤机机上的目标节点运行到距离端头10 m左右时，由UWB定位系统获得采煤机的三维位置坐标，为惯性导航校准提供基准。

图1 UWB基站部署Fig.1 UWB anchor nodes deployment

2 UWB定位方法

2.1 基站校准补偿

在UWB定位系统中，目标节点与基站的真实距离ri可表示为：

(1)

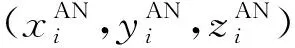
UWB信号在传输过程中受到测距系统本身的误差及非视距的影响，导致测量距离di往往大于真实距离，其数学表达式为：

di=(1+αi)ri+Bi+Ni+wi

(2)

其中：αi为尺度因子误差；Bi为偏差；Ni为非视距误差；wi为高斯白噪声。

系统误差可以通过适当的校准技术来进行补偿。 如果定位系统处于LOS环境下，则偏差和尺度因子误差可以得到补偿，通常情况下，假设基站的位置坐标是可以准确测量的。然而，在复杂环境下，在基站安装过程中和对基站坐标进行确定时存在误差，导致基站的坐标很难精准确定。因此，将式(2)改写为：

(3)

为了对基站进行位置校准，需要忽略非视距误差，在测量区域内选择多个参考节点，必须保证基站与参考节点处于LOS环境中，同时必须保证参考节点的位置坐标尽可能准确，则参考节点与基站之间距离di-j可表示为：

(4)

从式(4)可以看到，尺度因子误差、偏差和位置误差这3个误差参数相互交织在一起。由于采用相同的UWB，每个基站在LOS环境下偏差可以认为恒定不变，因此，用第j个测距方程减去第C个方程，消除偏差的影响，则有：

(5)

(6)

其中：

为方便计算，将上式简化为：

(7)

将式(7)转换成矩阵形式：

Ui=GiXi+W

(8)

根据最小二乘法原理，第i个基站的位置误差和尺度因子误差为：

(9)

根据基站位置误差，对每个基站进行校准补偿，可得校准后基站的位置坐标为：

(10)

为求得偏差Bi,令

(11)

H=[1, 1,..., 1]T

(12)

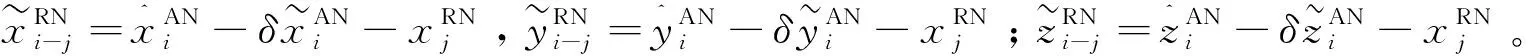
根据式(11)和式(12)，将式(4)转化为矩阵形式，如下：

Ri=HBi+W

(13)

由式(13)，可计算出偏差的估计值，即：

(14)

2.2 变分贝叶斯无迹卡尔曼滤波

根据上述方法，可以对每个基站的尺度因子误差、偏差及基站的位置误差进行补偿校准。对于确定的空间定位区域，每个基站被校准后，尺度因子误差和基站的位置误差是固定不变的。但是由于非视距的存在，偏差Bi和非视距误差Ni很难分开，非视距误差与定位空间的环境有密切的关系，存在不确定性和多变性，需要实时估计测距误差，因此采用VBUKF对测距值进行滤波，减小非视距误差的影响。

在k时刻，建立距离的空间状态向量模型为：

(15)

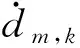
空间状态方程和观测方程为定义为：

Dm,k=FDm,k-1+Bwk-1

(16)

Zm,k=ADm,k+vk

(17)

(18)

(19)

(20)

其中，0<β≤ 1，0 < ||B|| < 1。

(21)

VB近似的思想是通过最小化后验近似分布与真实分布之间的Kullback-Leibler(KL)散度值[26]，可得相关参数最优估计，其散度定义为：

(22)

通过对式(22)散度值最小化，可得如下近似：

(23)

(24)

(25)

VBUKF的基本步骤如下：

1)协方差矩阵经过SVD分解后，如下：

(26)

2)计算2n+1个Sigma 点及相应的权重：

(27)

其中，λ=α2(n+δ)-n,λ和δ为尺度参数；α为一个较小的整数。

3)根据状态方程计算预测状态采样点：

(28)

(29)

(30)

量测噪声方差矩阵参数预测为：

基于HIS的住院摆药单优化与摆药差错预警系统的设计与应用 …………………………………………… 温正旺等（19）：2713

(31)

(32)

5)量测更新

(33)

(34)

(35)

(36)

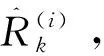
(37)

(38)

(39)

(40)

(41)

(42)

经过VBUKF滤波后，可获得滤波后的距离：

(43)

2.3 定位算法

当测距值经过VBUKF平滑后，结合校准补偿后的基站位置坐标和CL算法求解目标节点的估计位置，4个UWB基站组成的定位系统观测方程组为：

(44)

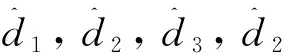
将式(44)转换成矩阵的形式：

CX=M

(45)

其中:

目标节点的位置坐标为：

X0=(CTC)-1CTM

(46)

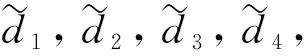
X=(HTH)-1HTL+X0

(47)

2.4 定位性能评价

为了评价UWB系统的定位性能，选择均方根误差(RMSE)作为定位精度的评价指标，计算公式为：

(48)

其中，(xr,yr,zr)为目标节点的真实坐标；(xt,yt,zt)为定位算法所求坐标；为全面分析误差的变化，x,y,z轴三个方向上的误差计算公式为：

(49)

3 试验结果与分析

为验证所提的校准方法和VBUKF的有效性，采用美国Time Domain公司生产的UWB P440模块作为基站和目标模块。4个基站固定不动，并将基站群在水平面的投影设置为V型布局，这种布局能获得好的定位精度[29]。为很好地模拟井下UWB定位系统对采煤机定位，并考虑非视距环境的存在，将一个基站设置在NLOS条件下，分别进行静态定位和动态定位试验，图2给出了基站部署及运动轨迹的平面图，图3为静态试验及动态试验的真实实验场景，4个基站的坐标分别为AN1 (3.636,6.062,0.478),AN2 (5.983,4.796,1.097),AN3 (3.598,6.033,2.179),AN4 (1.208,4.799,1.440)。为突出所提出方法的优越性，分别对CL算法和CL-GN算法校准平滑前后的定位精度进行分析。

图2 基站布局及运动轨迹Fig.2 Anchor nodes deployment and movement tracks

图3 现场试验场景Fig.3 Realistic experiment scenario

根据设置的基站坐标，在定位区域内选择9个参考节点，并且确保这些参考节点与每个基站处于LOS环境下，9个点的位置坐标尽可能的准确，根据上述基站误差补偿原理，可求出校准后4个基站的坐标，尺度因子误差和偏差，其求解参数见表1。

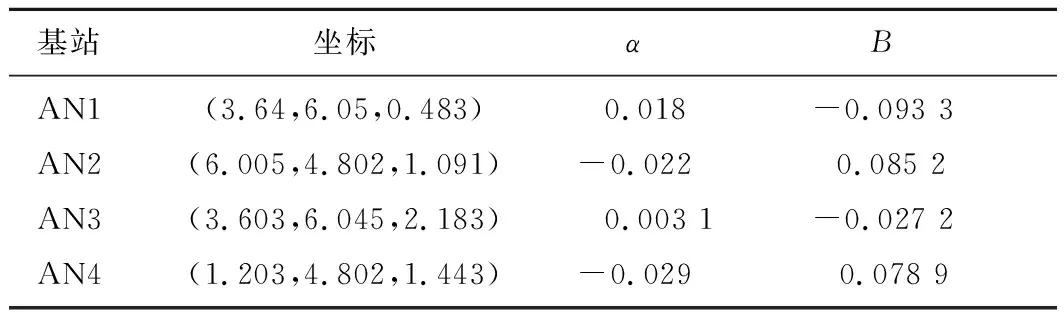
表1 校准后基站坐标、尺度因子误差和偏差Table 1 Coordinates,scale factor error and bias of anchor nodes after calibration

为验证NLOS环境下，VBUKF方法能够消除非视距误差，图4给出了AN2在第一个定位点的原始测距数据与VBUKF处理后的结果，从图中可以看到，原始测量数据波动较大，经过VBUKF平滑后，测距数据波动幅度明显减小，证明了VBUKF能提高距离精度和改善数据的稳定性，进而提升UWB系统的定位精度和可靠性。

图4 UWB测距信息Fig.4 UWB ranging information

在静态条件下，设置19个定位点，定位点的轨迹如图2所示，相邻2个定位点之间的距离为0.15 m,对每个点进行300次测距，根据4个基站所测得的距离，分别利用尺度因子误差α和偏差B对LOS条件下的测距进行重构，对NLOS条件下的测距值采用VBUKF平滑对距离滤波处理，利用CL算法和CL-GN算法分别计算校准前后目标节点的位置坐标，其定位结果如图5所示。从图中可以看到，无论是校准平滑前还是校准平滑后，GN算法都能够有效的减少误差；经过校准补偿和VBUKF平滑后，定位精度显著提升，而且CL-GN算法表现出较好的定位性能，定位精度在0.06～0.22 m，明显优于CL算法。图6给出了最大误差、最小误差、平均误差及误差标准差，经过校准补偿和滤波后，CL算法的平均定位精度提高了31.1%，CL-GN算法的定位精度提升了56.4%，而且CL-GN算法定位误差的标准差最小，仅为0.059 m，有利于UWB系统获得稳定的定精度。

图5 校准平滑前后定位误差对比Fig.5 Comparison the positioning error before and after calibration and smoothing

图6 定位误差特征统计Fig.6 Characteristic statistics of positioning errors

为进一步分析CL算法和CL-GN 算法校准前后误差在3个坐标轴上的变化情况，图7给出了误差在X,Y,Z3个坐标轴上的分布情况。从图7可以看出，无论校准前后，GN算法对3个坐标轴的定位精度有着很大的贡献，能够提高定位精度；Y轴误差明显大于X轴和Z轴误差，说明Y轴误差是引起定位精度较低的主要原因。未校准前，X轴能够获得较高的定位精度，Y轴和Z轴定位性能较差。经过校准平滑，CL-GN算法的Y轴和Z轴误差大大减小，定位精度大幅度提升，X轴的某些定位点定位精度变化不明显，但是满足实验室定位精度要求。在实际综采工况中，UWB定位系统可能会受到粉尘、水雾及采煤机运行时振动的影响，这些因素对定位精度产生怎么样的影响，有待进一步深入研究。

图7 校准平滑前后误差在三个坐标轴上的分布Fig.7 Errors distribution on three axes before and after calibration and smoothing

为更好地证明所提校准补偿和VBUKF平滑方法的适用性和有效性，本文进行动态试验，根据测距结果和CL-GN算法，分别计算出校准平滑前后的定位结果。从图8种可以看到，经过校准平滑后，目标节点在3个坐标轴上的波动程度有所较小，运动轨迹更加接近实际轨迹，证明了本文所提的校准方法能够有效减小定位误差，提升动态定位精度。在实际应用中，安装在机身上的目标节点可能会受到采煤机震动的影响，需要将目标节点安装在振动较薄弱的地方，振动、粉尘、水雾对UWB系统定位精度的影响需要进一步的研究。

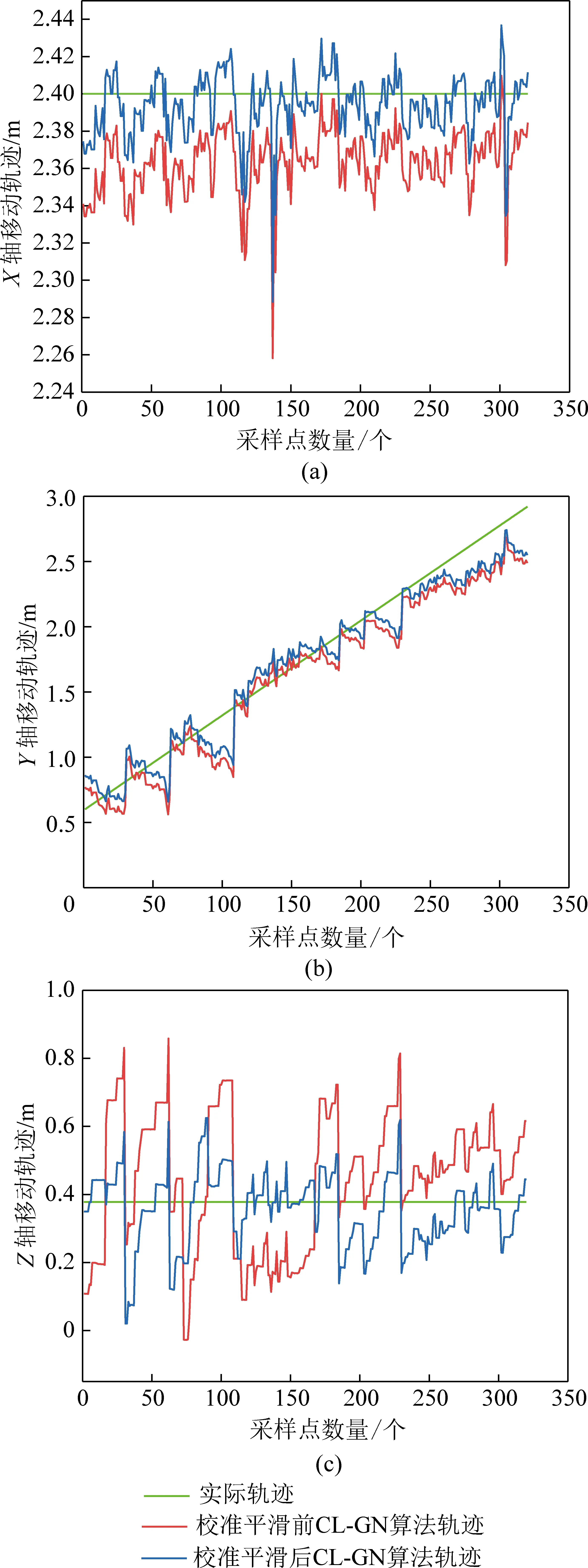
图8 校准前后动态定位结果轨迹曲线Fig.8 Trajectory curve of dynamic positioning result before and after calibration

4 结 论

1)为提高UWB系统的定位精度，考虑基站位置误差、尺度因子误差和偏差对定位精度的影响，提出对基站的位置误差进行校准补偿，根据校准补偿原理，可以获得校准后基站的坐标。

2)采用VBUKF对NLOS测距信息进行滤波处理，减小NLOS误差的影响，提高距离估计精度；在校准补偿和VBCKF平滑基础上，采用 CL算法求得目标节点的坐标，利用GN算法对CL算法的结果进行优化。

3)试验结果表明，经过校准补偿和VBUKF平滑后，CL和CL-GN算法的平均定位误差分别由0.347、0.250 m减小为0.239、0.109 m,平均定位精度分别提高了31.1%，56.4%；同时动态运动轨迹更加接近实际轨迹，表明本文的方法能有效地提升UWB系统定位精度，是一种可行的方法，能够为井下定位技术提供理论参考。