基于ADAMS的螺栓拆卸机器人动力学分析与仿真

刘 数，尚 欣，高希振，孙传虎，王 冠

（宁夏大学 机械工程学院，银川 750000）

0 引言

动力学是机器人控制与设计的基础，工业机器人作为串联式多关节机构，拥有多个输入输出，为非线性强耦合关系，是一种典型的多体机械系统[1]。伴随拆卸类工业机器人高精度、智能化的发展趋势，使其对控制和结构设计方面的要求更高。动力学的分析与仿真作为拆卸机器人设计是否合理的重要判别工具，不仅可以提高控制的精度与稳定性[2]，也是结构设计过程中，各个关节驱动电机与减速器选型的主要依据[3]。曾有鑫[4]、何倩倩[5]、孙恒辉[6]等人对拆卸类机器人动力学进行了相关研究，以验证结构设计的合理性及奠定了优化控制的基础。动力学分析与仿真在设计与生产上的应用同时具有缩短产品研发周期，减少物理样机试制，降低研发成本等优点，也逐步受到了人们的重视[7]。

当前关于机器人动力学主流的分析方法为拉格朗日法[8,9]、牛顿-欧拉法[10,11]、凯恩法[12]等，而动力学仿真主要是，借助计算机仿真软件进行系统动态仿真,常用的动力学仿真软件包括ADAMS、Simpack、SimMechanics等[13]。其中,ADAMS软件以其强大的求解功能和便捷的交互式图形环境,成为当前使用最广泛的多体动力学仿真软件[14]。因此，为验证拆装工业机器人结构与动力选型是否合理，保证该工业机器人控制方面上精度与稳定，针对本文自主设计的六自由度螺栓拆卸工业机器人，采用拉格朗日法建立研究对象的动力学数学模型，利用MATLAB对其数学模型系数进行分析，然后借助ADAMS软件进行动力学仿真，完成了机器人动力学的理论分析与仿真验证。

1 三维建模与结构参数

针对实际拆装工况需求，鉴于对其末端执行器的姿态要求，确定为具有六个自由度的串联式机器人，前三自由度确定末端执行器所到达的位置，后三自由度确定末端执行器姿态要求，考虑ADAMS的建模功能较为繁琐，为了能够快速准确的建立机器人三维模型，选择CAXA实体设计软件依据设计图纸进行三维建模。机器人模型如图1所示。

图1 机器人三维模型

整个机器人机构由基座、肩关节、大臂、小臂、手腕等关键机构组成，前四关节为RV减速，后两关节为谐波减速，电机选择安川电机。结构参数依据工作空间要求，确定为大臂长度990mm，小臂长度1240mm。主要的动力学参数如表1所示。

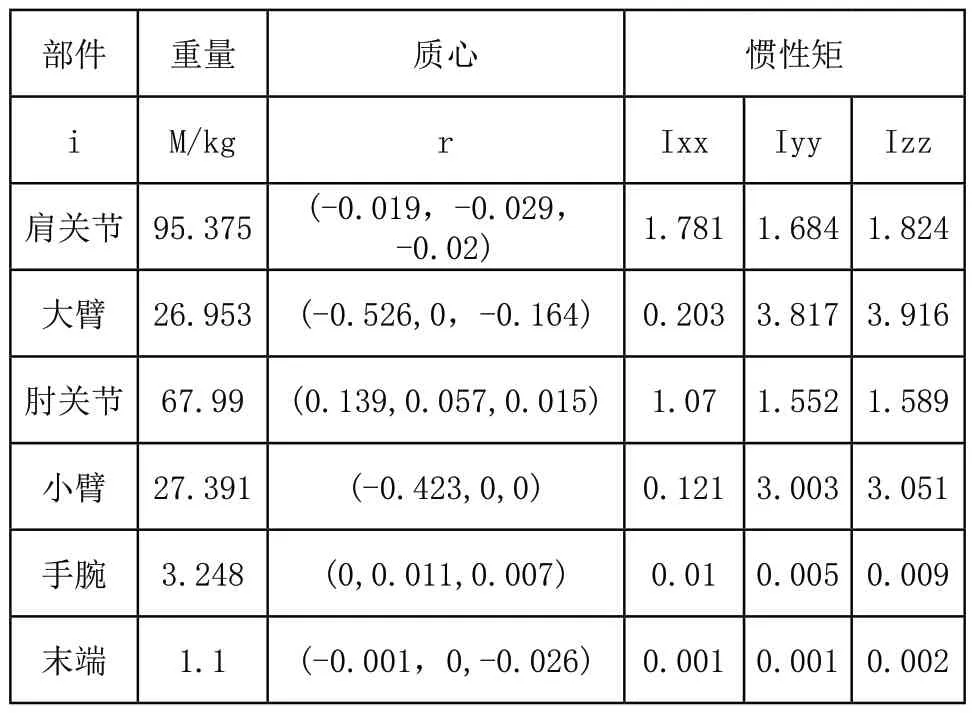
表1 主要动力学参数

拆卸机器人对球阀螺栓的拆卸，主要是通过机器人末端执行装置对螺栓进行拆卸，末端执行装置是采用二次包络蜗轮蜗杆结构形式的液压扭力扳手，机器人首先将拆卸头对准待拆螺栓，然后进一步调整姿态，使反作用力板临近球阀本体，以抵消拆卸产生的反作用力对机器人产生的负载冲击，最后液压驱动末端执行机构将螺栓旋松去除，如图2所示。

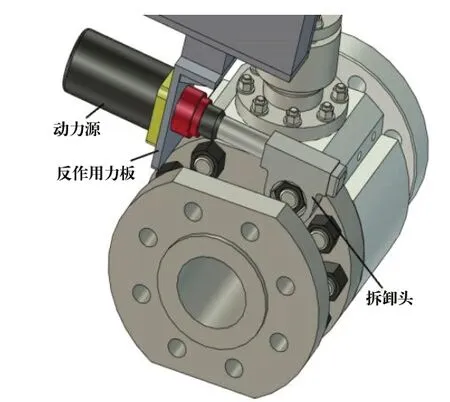
图2 执行机构工作示意图

2 动力学数学建模

动力学分析的方法有很多种。但鉴于拉格朗日法是一种基于能量的动力学方法，只需要速度和势能而不需要求出内外作用力，能够以简单方便的形式进行动力学方程的推导。故本文采用拉格朗日法对其进行动力学推导。

依据拉格朗日方程函数的定义[15],动力学结构形式如式(1)所示：

式(1)中L为拉格朗日函数，qi为系统选定的广义坐标，针对本文中的研究对象其单位取rad，Ek为系统动能，Ep为系统势能。

其机器人上任一连杆任意一点的速度为：

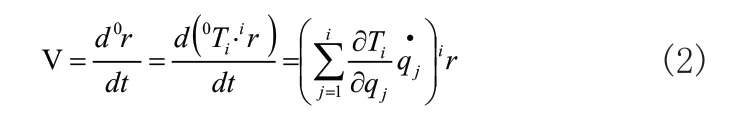
任意一点的动能为：

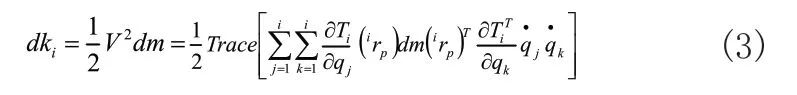
任意连杆的动能为：

机械臂的拉格朗日方程为：

系统的动力学方程为：

上式进一步写成机器人动力学的经典形式：

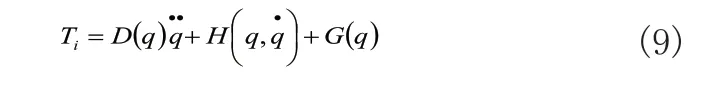
其中：

惯性矩阵D(q)=[Dij]，

重力矢量矩阵G(q)=Di。

以上数学结构相对简单，但针对多自由度机械臂而言，数学模型仍相对复杂，不利于分析验证，对于当前研究的六自由度的工业机器人而言，鉴于后三自由度满足pieper准则，手腕机构可与小臂作为一个整体进行分析，其大臂与小臂的状态会对最终的动力学分析结果有着决定性的作用[16]，加之肩关节是对其各主要结构动力学累加，故本文分析了大臂与小臂的状态对肩关节相对动力学的各系数主要矢量数值分布情况。如图3～图5所示。

图3 肩关节重力载荷

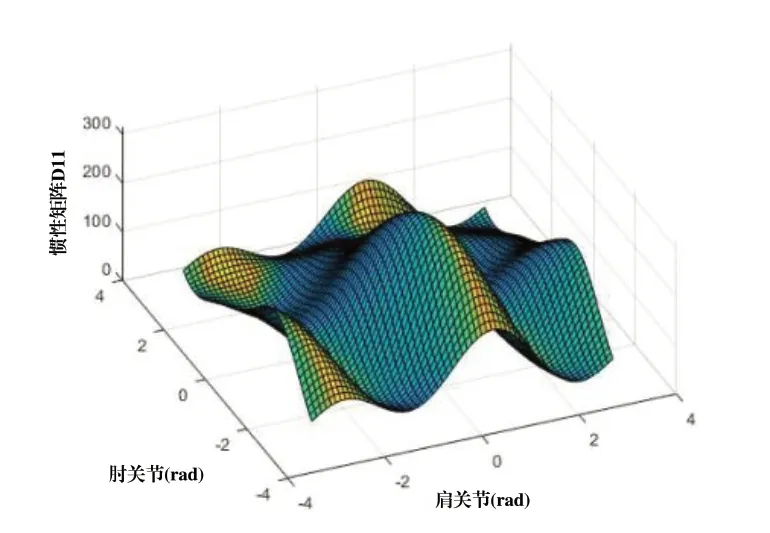
图4 惯性矩阵D11

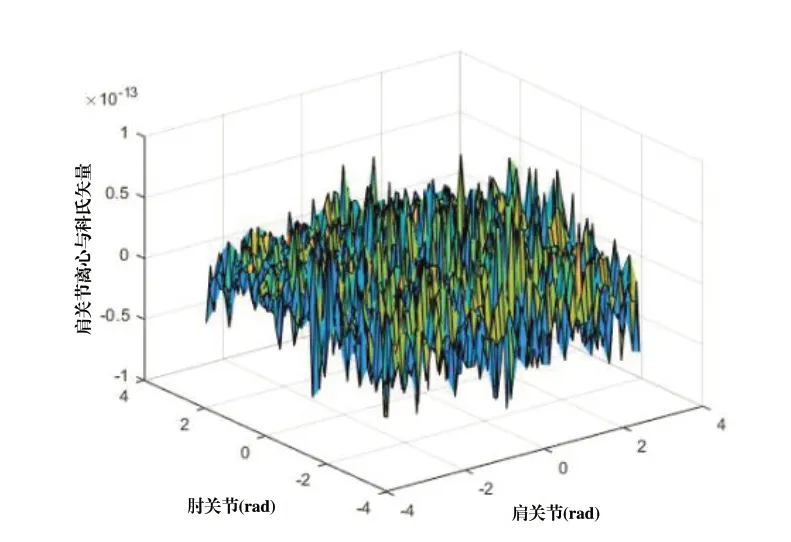
图5 肩关节离心力与科氏力矢量

由图3～图5可知，其肩关节的状态对肩关节重力载荷与系数的取值影响较大，离心力与科氏力分析中赋予了肩关节2rad/s的角速度，因离心力与科氏力较为复杂，无明显规律，但其总体数值较小，在本系统中非高速运转的状态下，可以忽略不计。

3 仿真过程

首先将CAXA实体设计软件中的机器人三维模型的装配体输出为Parasolid格式文件，并将其导入ADAMS中，将导入ADAMS的三维模型，进行添加材料、质量属性、布尔操作等编辑，以便可以更快捷、准确的模拟实际的系统。各关节设置为转动副，基座与大地固定，对转动副添加驱动。拆卸机器人在工作过程中，其运动状态有无数种，仿真过程不可能对所有的状态进行仿真分析，只能选择相对典型又尽可能涵盖大部分路径与姿态[17]，驱动函数借助STEP5函数进行驱动设置。处理后的虚拟样机如图6所示。

图6 虚拟样机仿真模型与运动轨迹

仿真完成后，利用ADAMS的后处理模块可输出各个关节的驱动力矩等运动过程中的仿真参数，各关节力矩曲线如图7～图10所示。

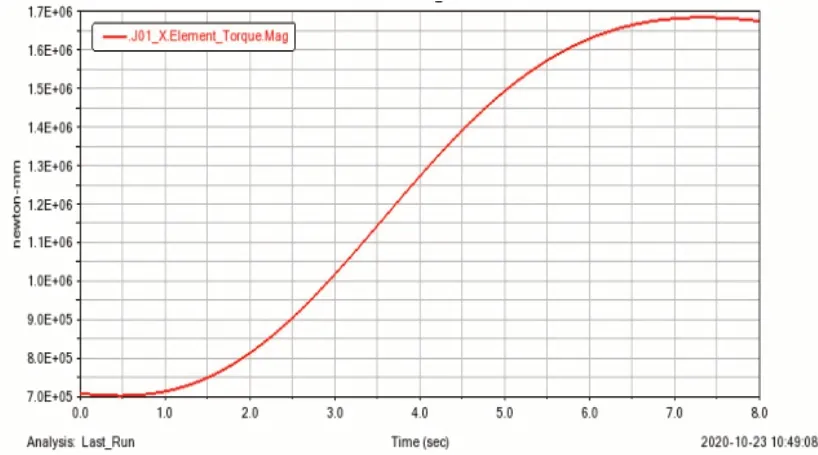
图7 第一关节力矩图

图8 第二关节（肩关节）力矩图

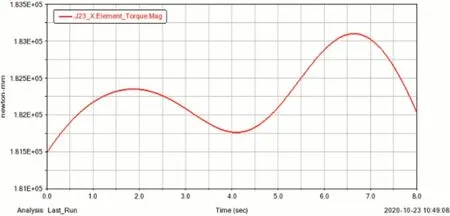
图9 第三关节（肘关节关节）力矩图

图10 后三关节力矩图

由图10可知，其主要关节中，第一关节力矩变化范围为700～1700NM；第二关节（肩关节）力矩变化范围为95～116NM；第三关节（肘关节）力矩变化范围为181～184NM，各关节力矩总体而言起伏变化较为平稳，无突变情况，力矩变化区间范围合理，符合设计需求。

4 结语

本文首先利用CAXA实体设计软件依据设计要求，建立了拆装工业机器人的三维模型，基于拉格朗日动力学方程对其工业机器人的动力学数学模型进行了推导，并对动力学模型中的系数进行分析；在动力学仿真上，运用多体动力学虚拟仿真软件ADAMS对其进行了仿真分析。分析与仿真结果显示：该拆装机器人运动稳定，符合设计要求。同时依据数学模型与ADAMS虚拟样机对结构进行动力学仿真与分析的方法，可以有效的提高设计开发效率，降低生产与实验成本。