基于SuperMap的卫星虚拟仿真系统设计与实现

高凡，王彦良，陈富强，吴薇，何家琦，白天琦

（1.郑州师范学院，河南 郑州 450053；2.河南省地质矿产勘查开发局测绘地理信息院，河南 郑州 450006）

我国航天卫星事业迅猛发展，越来越多的卫星发射升空；但人们对卫星的了解大多源于书面文字、新闻报道等层面，不够直观和立体。本文基于Super-Map iDesktop 9D软件设计并实现了卫星虚拟仿真系统，可帮助人们直观研究卫星轨道控制和仿真。自20世纪50年代以来，美国已开始对卫星轨道控制和仿真进行研究。Winorbit是美国为研究卫星轨道跟踪和预报而设计开发的一款实时计算卫星位置并使用二维地图显示卫星轨迹和覆盖区域的软件系统[1]。该系统采用二维的方式进行展示，在视觉上并不能对航天器、地球和太阳的时空关系，航天器的瞬时姿态以及位置上的转变进行直观反映，视觉效果呈现较差；还需有牢固的专业知识背景才可顺利解读，因此并未被广泛应用。Satellite Tool Kit（STK）由美国Analytical Graphics公司研发，被世界多国航天专家应用于卫星系统工程的设计、制造、发射和运行的过程中。作为一款具有商业化性质的航天卫星系统分析软件，STK可帮助用户快速了解空间飞行任务中多学科交叉内容，能十分便捷地帮助用户制定飞行计划，分析飞行任务和卫星实时的机动情况[2]。通过该软件系统，用户仅需设置各类运动物体的相关参数即可快速地对任务过程进行模拟和显示；再根据软件生成的相关数据报告和图片表格开展任务分析，从而得出最佳的解决方案。然而，由于STK是商业软件，价格十分昂贵；且STK未公开源代码，因此不能自主进行软件的二次开发，进而适应和满足国内部分卫星飞行方案中的特殊要求。

我国航天科技工作者在理论与实践中形成了多种卫星轨道控制与仿真方法，从不同角度探索了卫星的最优飞行路线，也开发了许多仿真系统。本文根据已获取的TLE数据，计算得到卫星在地惯坐标系下的瞬时坐标，再将瞬时坐标转换为地固坐标系下的坐标，最后利用SuperMap iDesktop 9D创建轨道数据集，添加坐标点要素，连接坐标点，形成卫星轨道。通过该软件的二次开发，将3ds格式的卫星模型加载到场景中，并动态设置坐标，实现卫星在轨运转的可视化。

1 系统参数与基准

1.1 卫星轨道根数

卫星轨道根数用于描述卫星运转的参数信息。研究卫星运动状态的6个参数（轨道半长轴a、轨道偏心率e、轨道倾角i、升交点赤经Ω、近地点幅角ω、真近地点角f），简称卫星轨道六根数[3]。通过轨道六根数可确定卫星在轨道上的位置和速度等参数[3-4]。

1.2 时间系统

时间系统是卫星定位和测量过程中的一个重要概念，在本系统中涉及任意时刻协调世界时与儒略日的转换，以便计算格林尼治平恒星时。

1.3 空间坐标系统

本系统中采用两个不同的参考系：①地心地固坐标系，坐标原点为地心，如图1所示；②地心惯性坐标系，坐标原点为地球质心[5]，如图2所示。

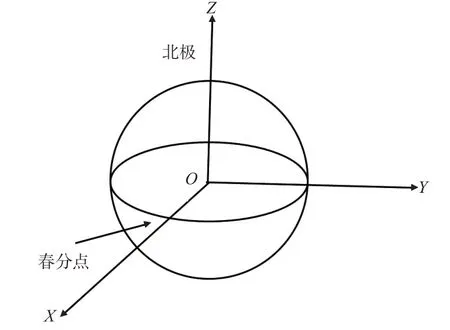
图1 地心地固坐标系

图2 地心惯性坐标系

2 卫星轨道地理坐标解算

在计算卫星位置和速度之前，需对各坐标系进行坐标转换。由TLE数据计算得到的卫星坐标是地心惯性坐标系下的大地直角坐标，而SuperMap iDesktop 9D中采用的是地心地固坐标系下的地理坐标，因此需首先将计算得到的地心惯性坐标系下的大地直角坐标转换为地心地固坐标系下的大地直角坐标，再将地心地固坐标系下的大地直角坐标转换为地心地固坐标系下的地理坐标。坐标转换前，需先计算卫星位于该坐标点时刻的儒略日，再根据儒略日计算得到恒星时角，最终根据恒星时角进行坐标转换。

2.1 儒略日与协调世界时的转换

在卫星轨道计算中，首先需将公历表示的年、月、日表示为儒略日，转换公式为：

式中，[]为取整；JD为转换后的儒略日；Y为公历年份；M为公历月份；D为公历日；h为小时数；m为分钟数；s为秒数[6]。

2.2 儒略日与格林尼治平恒星时的转换

计算得到儒略日后，再利用儒略日计算得到儒略世纪，进而计算得到格林尼治平恒星时。其计算公式为：

式中，T为儒略世纪[4]。

2.3 计算格林尼治视恒星时角

首先利用格林尼治平恒星时计算格林尼治视恒星时角，再利用格林尼治视恒星时角将地惯坐标系转换为地固坐标系，最后将地固坐标系转换为地理坐标系。其计算公式为：

式中，Δψ为黄经章动；Λ为月亮轨道对黄道平均升交点的黄经；T为历元J2000起算的儒略世纪数[5]；εA为平黄赤交角。

2.4 地心惯性坐标系与地心地固坐标系的转换

地心惯性坐标系与地心地固坐标系的转换公式为：

2.5 地心地固坐标系与地理坐标系的转换

地心地固坐标系与地理坐标系的转换公式为：

式中，N为基准椭球体的卯酉圆曲率半径；e为椭球偏心率。

3 系统设计与实现

3.1 系统设计

通过SuperMap桌面端iDesktop建立三维地球场景，利用iObject.NET和Visual Studio 2012进行二次开发，具体包括加载卫星模型、绘制卫星轨道和卫星模型的人机交互等步骤，最终形成完整的系统。系统设计流程为首先根据获取的TLE数据计算卫星所必需的轨道要素，逐个计算得到卫星在某时刻的位置点；然后连接各位置点形成三维轨道线；再将卫星模型加载到三维模型可视化线上；最后实现卫星在轨运行过程的可视化。通过鼠标点击选取卫星模型，采用气泡的方法展示卫星的具体信息，实现人机交互，如图3所示。

图3 系统设计流程图

3.2 系统实现

3.2.1 卫星仿真系统的可视化环境

SuperMap iDesktop 9D是一款桌面GIS应用与开发软件，几乎涵盖了常规的GIS功能（如iServer服务发布、自动化制图、空间分析、网络分析、地图发布、海图模块等）以及现有的较专业的工具功能，且还支持扩展开发[7]。系统基于SuperMap iDesktop 9D软件提供的三维地球场景，完成可视化环境的创建，并实现初始化处理、加载3ds卫星模型、绘制卫星轨道等功能。系统采用Visual Studio 2012平台进行二次开发，不仅可以自由浏览查询卫星信息，还可以通过控制按钮设置自定义的观察视角，最终实现卫星、发射场地、卫星运行轨道的可视化和信息查询。

3.2.2 卫星轨道三维虚拟仿真的实现

在卫星虚拟仿真系统中，地球三维模型的建立是一项基础且重要的工作。系统以SuperMap iDesktop 9D软件的球面场景为地球三维模型进行研究。系统程序是基于面向对象计算开发的，开发语言为C#，编程环境为Microsoft公司的Visual Studio 2012，配置环境为SuperMap iObject.NET。系统实现的具体步骤为：

1）三维模型建立。利用3ds Max创建卫星模型和卫星发射基地模型，通过Photoshop修改贴图，并与卫星原图进行细致比较，制作较逼真的卫星模型和卫星发射基地模型，如图4、5所示。

图4 卫星发射基地三维模型

图5 卫星三维模型

2）开发环境配置。在SuperMap iDesktop 9D桌面端软件中创建新的工作空间（Satellite.SWMU），右键单击场景菜单，建立新的球面场景，命名为satellite。配置iObject.NET环境，安装SuperMap Visual Studio 2012工具包，利用Visual Studio 2012建立C#项目，进行桌面端SuperMap iDesktop 9D的二次开发，链接工作空间。

3）卫星轨道可视化的实现。

首先计算不同时间下的卫星瞬时坐标，卫星在轨运行时位置随时间的变化而改变，因此将时间设置为变量，计算不同时间下的卫星瞬时坐标。将时间步长TimeStep设置为1 d，BeginTime设置为获取电脑本地时间_time64(NULL)，为了减少计算机数据处理量，End-Time设置为BeginTime+1，则位置点个数NumPoints=int(3 600×24(dEndTime-dBeginTime)/dTimeStep)。计算卫星瞬时位置的关键在于，计算参数真近点角（True-Perigee），由此计算得到不同时间下的卫星位置点坐标。

在计算TruePerigee时，需运用偏近点角（Bias-Perigee）和平近点角（FlatPerigee）两个辅助参数。其计算公式为：

通过对应公式计算得到地惯坐标系的位置点坐标。其计算公式为：

上述计算得到的点坐标为地心惯性坐标系下的大地直角坐标，需将其转换为地心地固坐标系下的大地直角坐标，再将地心地固坐标系下的大地直角坐标转换为地理坐标。

然后绘制三维轨道线，将转换后的点坐标导入point3ds中；再将point3ds加载到geoline3D上，并设置三维线的颜色、宽度以及海拔；最后把三维线加载到Scene中实现三维线的可视化。

4）模型加载与卫星在轨运行可视化实现。将3ds格式的卫星模型加载到三维线上，并设置模型运动周期，实现卫星在轨运行可视化。导入不同卫星的TLE数据，即可计算不同卫星的轨道，并加载对应的卫星模型实现三维可视化，如图6所示。

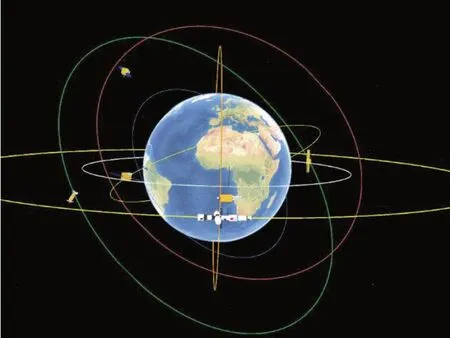
图6 卫星加载示意图

5）卫星信息显示。在系统中通过鼠标单击选取卫星模型可弹出对应的卫星信息，该交互通过气泡方式实现。气泡由外框和绘图区两个部分组成，将用户自定义控件传入绘图区，在控件中可设置气泡的样式和显示内容等；通过代码链接模型ID与气泡控件，实现卫星信息的气泡显示。在主程序中建立新的用户自定义控件，从工具箱中拖入pannel控件作为气泡的主面板，拖入picturebox控件用以展示卫星照片，拖入label控件用以展示卫星名称，拖入textbox控件用以介绍卫星的具体信息，拖入linklabel控件超链接用以展示更多的卫星信息；初始化气泡，填充气泡信息，链接控件与SuperMap桌面端中填写的属性信息；最终实现卫星虚拟仿真系统。

4 结语

系统采用SuperMap iDesktop 9D进行卫星仿真，利用Visual Studio 2012进行二次开发，绘制了卫星轨道，显示了卫星的基本信息。使用者不局限于专业人士，可以向任何人展示，方便传播，有利于激发不同人群对航天的兴趣和关注度。系统的显示方式为三维图像，以地球外部为立足点，非常直观生动；但由于SuperMap iDesktop 9D中的三维地球无法实现地球自转，因此系统只能模拟地球停止自转情况下的卫星在轨运动状态。