基于TOPSIS评价法的企业原材料订购决策研究
方洋洋 向佳豪 张立 冯高尧
(1.汉江师范学院物理与电子工程学院 湖北十堰 442000;2.汉江师范学院新型功能材料制备与物性研究中心 湖北十堰 442000)
随着社会科技时代的进步,各种生产企业相继建立与发展。生产原材料的需求订购与运输方面所存在的问题也表现得愈加突出。为了解决现实生活中企业生产原材料中表现的订购决策问题,对该问题所存在的现状进行分析,在考虑企业的订购问题时,其中材料的选择,供货商的选择,运输商的选择以及各种影响产品产量质量的损耗都是生产企业在制定方案时需要考虑的问题[1-4]。
通常来说,对于生产企业原材料中的订购发现,供应商收到的订货总量与企业对该商家的偏好程度是成正比的,所以企业总是会偏好选择能够保障其生产的商家。供应商实际的供货量与企业的订货量总是不可避免地存在偏差,而对于偏差的程度、偏差的范围、异常偏差发生的次数相较于总交易次数的比例,在一定程度上也反映了供应商对于保障该企业生产的重要性。
基于以上方面的分析,考虑减少待选择企业的数目。基于供货商的供货能力,近5年企业对于各个原材料供应商的订货总量,排除订货总量极低的供应商。以分析供货商的供货特征,确定供货次数、平均供货量、单次最大供货量、供货稳定性、供货一致性和合理供货比例,这六个评价指标作为衡量选择订购方案优劣的属性变量。利用TOPSIS评价法建立起多目标评价模型来量化各供应商对于保障企业原材料生产的重要性,从而选择出最重要的50家供应商[5]。
1 企业原材料订购决策模型建立
1.1 建立供货商选择指标模型
1.1.1 供货次数
供货次数越多,证明供货商供货能力越强,企业对于供货商的供货能力认可度也就越高。
基于供货商供货数据计算供货总量。计算各供货商过去五年参与供货次数:
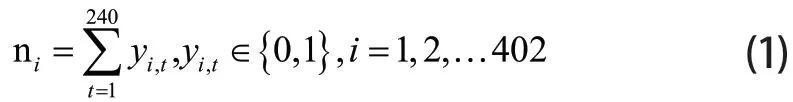
式(1)中:ni表示供货商i在近五年供货次数,逻辑变量yi,t,含义为在第t周供货商i是否参与了供货,“1”表示参与供货,“0”表示未参与供货。
1.1.2 平均供货量
由平均供货量可以看出供货商的供货质量与供货能力。
先对原材料进行换算,再进行平均供货量的计算,统一为生产数目,剔除240周内未参与供货数据,最后求得平均值:

式(2)中:m i表示供货商平均供货量,p i表示产品生产一立方米时所消耗的原材料,xi,t为供货商i第t周的供货量,A、B、C为各类原材料的供货商集合。
1.1.3 单次最大供货量
由于供货商会根据企业对产品的需求量拟定最大生产量,所以它会反映出一个供货商供货量的最大上限值。
由所给供货商历史供货数据将原材料换算为生产产品数目,最后得出各家供货商历史供货数据最大值:

式(3)中:ximax表示供货商i的单次最大供货量。
1.1.4 供货稳定性
为了减少企业不必要的损失,供货商供货需要参照企业每次的订单量上下浮动。供货稳定性越好,证明供货商供货能力越强。
为了得到各供货商稳定性,可以对各供货商每次供货量与订货量的差值进行比较:
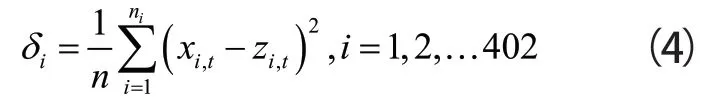
式(4)中:δi代表供货商i订单量与订货量均方误差,zi,t表示供货商第t周的供货量。
1.1.5 供货连续性
通过平均间隔天数、平均连续供货周数和间隔次数三项指标最终得出供货连续性最好的供货商。
分析发现,平均间隔天数和平均连续供货周数可视为效益指标,间隔天数可视为成本指标。分别归一化:
成本指标:
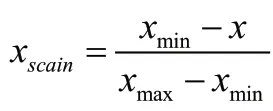
效益指标:
指标归一化后,可建立供货连续性评价指标并由熵权法求解:
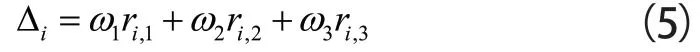
式(5)中:ωj表示第j个指标的权重,ri,j表示供货商i第j个指标数值。
1.1.6 合理供货比例
合理供货比例是指供货商供货量与企业订单量比值,合理供货比例越大,则与企业合作可能性就越大。
此处设定理想供货商供货量应在企业给定订购单量上下20%范围内浮动。可得到:
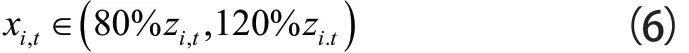
式(6)中:xi,t为供货商i第t周的供货量,zi.t表示供货商i第t周的供货量。
定义供货符合时即为1,不符合即为0,可以得到:

式(7)中:Counti表示供货商符合条件的供货次数。
最后,供货商i的合理性比例可以由符合条件的供货次数占供货商供货总次数比值求得:

式(8)中:γi表示供货商i的合理性比例。
1.2 建立TOPSIS法多指标评价模型
本文描述在面对订货方案的优化选择时,采用熵权法和TOPSIS两者结合的方式进行最优目标求解。
熵权法的主要目的是对指标体系进行赋权,而TOPSIS的主要目的是通过逼近理想解的程度来评估各个样本的优劣等级。将两者结合,先是对该原始数据进行整理和处理,并且计算出指标样本中的比重和权重,再进行综合评价,根据所得计算数值评价得出优劣等级进行归一化处理,让各个指标逐渐去接近甚至是达到最优值,构造出两者的相近度,然后对相近度进行排序,排序用表示,的值越大,表明评价对象越接近最优值。

图1 TOPSIS法多指标评价模型
1.2.1 熵权法
根据信息熵的定义,对于某项指标,可用熵值来判断某个指标的离散程度,信息熵值越小,该指标对综合评价的影响(即权重)就越大。利用信息熵,计算各个指标权重,为多指标综合评价提供依据。
(1)对样本数据求比值,可得:

式(9)中:xij表示第i个样本第j项评价指标的数值;Pij表示样本数据比值。
(2)代入计算能够求得熵值得:

式(10)中:ej表示样本数据熵值。
(3)进行定权计算比重和归一化处理,可得:
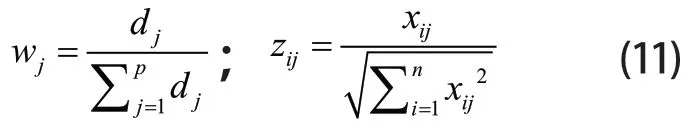
式(11)中:wj表示权数比重,dj表示每个指标相应的权重,zij表示归一化权重值。
1.2.2 TOPSIS评价法
TOPSIS法[4]根据有限个评价对象与理想化目标的接近程度进行排序的方法,对现有的对象中进行相对优劣的评价。TOPSIS法是多目标决策分析中一种常用的有效方法,所用的是欧式距离。其基本原理,是通过检测评价对象与最优解、最劣解的距离来进行排序,若评价对象最靠近最优解同时又最远离最劣解,则为最好;否则不为最优。其中最优解的各指标值都达到各评价指标的最优值。最劣解的各指标值都达到各评价指标的最差值。
(1)对数据进行预处理,寻找最优、最劣方案:


式(13)中:D i+表示最优距离,D i-表示最劣距离。
(3)再构造相对接近度:

式(14)中:C i表示相对接近度。再根据Ci的大小进行排序,Ci越大,表明评价对象越接近最优值。
2 企业原材料订购决策模型求解
假设最重要的供货商供需可确保企业正常生产运行。首先,由供货量大于订货量“,富余量大于0”这一条件,在402家供货商里面剔除一部分不符合条件的供货商。
其次,由熵权法求得六个基本评价指标的系数,由“供货次数、平均供货量、单次最大供货量”这三个指标确定供货商供货能力,由供货稳定性、供货一致性和合理供贷比例确定供应风险。再由各指标系数权重确定影响比重最大的相关指标,从而确定供货商供货能力和供货风险两个要素对供货商选择的影响。
最后,运用TOPSIS法对给定402家供货商进行细化处理,由评分最高的前50家供应商确定订货方案。
3 案例分析
本文主要以2021年大学生数学建模国赛C题生产企业原材料的订购与运输为背景,探究解决企业原材料的订购方案,筛选出合适的供货商以确定订购方案。
已知企业每周有2.82万立方米的产能。单独生产每立方厘米材料时,需要A、B、C类原材料分别为0.6立方厘米、0.66立方厘米、0.72立方厘米。企业仓库要储存满足两个星期生产的原材料,同时收购供货商的全部供货。
利用MATLAB软件编程,对熵权法进行求解,代入式(5)可得:

式(15)中:间隔次数权重为0.4383,平均间隔周数为0.3560,平均连续供货周数为0.2057。由上式各系数可知:间隔次数和平均间隔周数对供货连续性影响最大,决定供货连续性的主要指标为间隔次数。
TOPSIS评价法六个指标权重计算如表1所示:
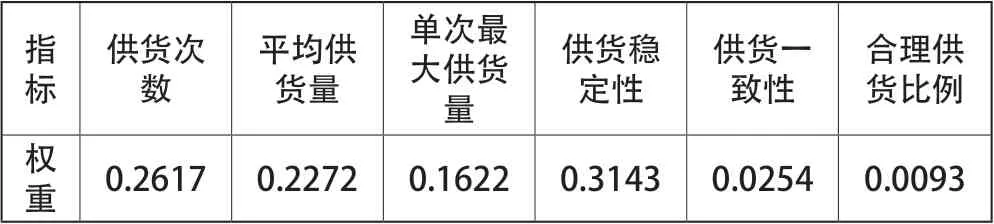
表1 TOPSIS评价法指标权重
由表1数据可知:供货稳定性权重最大即对供货商选择影响最大,供货次数第二。由前文筛选指标流程可知,两个指标分别决定供货商供应能力和供货风险。
最终由上述公式计算得到可靠性最大的前五十名供货商如表2所示。
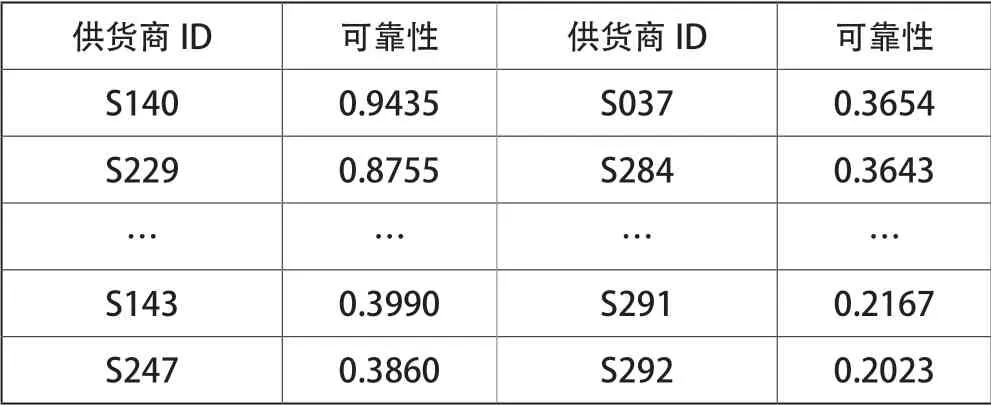
表2 50家可靠五十家可靠性最大供货商
由50家供应商的可靠性可以看出,供应商S140的可靠性最大,高达0.9435,对于今后订货方案的确定,可以优先考虑。前六家供货商的可靠性都比较强,之后则呈现断层式衰减,因此前六家供货商可以制定长期合作方案,之后的供货商则可用作备用方案选取。
4 结语
本文围绕供货数据和订货历史,对供货商范围进行缩小,从平均供货量反应了供货商长期合作的价值及间接判断出供货商供货质量与供货能力,筛除出可靠性较大的供货商方案。
(1)根据订货的各种因素建立相关指标模型,包括供货次数、平均供货量、单次最大供货量、供货稳定性、供货一致性和合理供货比例。
(2)采用熵权法可以得到指标权重系数,根据权重系数进而建立TOPSIS法综合评价模型。
(3)通过TOPSIS法建立多指标评价模型,得出优劣等级进行归一化处理,依据可靠性大小筛选出50家最重要的供货商。由TOPSIS法算出的结果可运用于最优解的评定,还可用于对比所求目标特性的优良。

