高速公路同向曲线路段车辆行驶轨迹研究

张军华， 郭筱穆

(1.安徽省交通规划设计研究总院股份有限公司，安徽 合肥 230088； 2.公路交通节能环保技术交通运输行业研发中心，安徽 合肥 230088； 3.国家开发银行辽宁省分行，辽宁 沈阳 110014)

0 引 言

近年来，我国高速公路迅猛发展，并将战略重心放在“老少边穷”地区。这些地区往往地形崎岖复杂，在设计时会受到多方面的限制，因此在设计的过程中需要在满足规范的前提下进行设计指标的相应调整。公路平面线形由直线、圆曲线及缓和曲线三种线形单元组成，路线设计规范[1]对不同组合形式下的各基本单元做出了相应的要求。平曲线由于能够避免长直线引起的驾驶疲劳和更好适应地形的优点，成了平面设计的主要组成部分。但是，平曲线也会由于增加了驾驶员的操作难度而引发相关的安全问题。有关资料表明，大部分交通事故发生在平曲线路段，在美国达到40%，在中国达到36%[2]。因此，平曲线的设计对于公路平面整体的安全性具有重要的影响。平曲线路段是由圆曲线+直线+圆曲线构成的，主要包括同向曲线与反向曲线两类，本文的研究对象为同向曲线。同向曲线指的是两个转向相同的相邻圆曲线中间连以直线所形成的平面线形。同向曲线在设计时主要需要考虑曲线间的短直线长度，因为曲线间直线长度过短会引起驾驶员的视觉误判，容易从视觉上忽略，而把两个曲线看成一个曲线；当直线长度不足以将两个曲线完全独立时，容易把中间的直线段看成反弯的断背曲线[3]，这对车辆的安全行驶产生了严重的影响。

目前国内外对于同向曲线间最短直线长度的要求都有相应的规定。我国规范规定[1]两曲线间以直线径相连接时，直线的长度不宜过短，设计速度大于或等于60 km/h时，同向曲线间最小直线长度(以m计)以不小于设计速度(以km/h计)的6倍为宜。美国对最小直线长度没有进行规定[4]，而是根据不同的设计速度对平曲线长度提出不同的要求。日本对于同向曲线间的短直线长度也未做出规定，有日本学者通过透视图检查，同向曲线间直线长度最好避免在500～700 m。德国作为世界上最早对最短直线长度进行规定的国家，提出了最小长度为设计车速6倍的要求[5]。我国现行的规范则是主要参考了德国规范的取值，但是对于这一取值的具体意义没有进行相应的解释说明。国内学者对于同向曲线间的短直线合理长度进行了深入的研究，早期张正云和刘遵纪[6]从力学、舒适性和经济性角度对断背曲线的定量问题进行探讨，认为力学条件对定量断背曲线没有控制意义，当直线长度达到设计车速的6秒行程以上就能满足驾驶员操作需要，从驾驶员视觉连贯性和舒适性方面考虑才有了6倍速度(6V)的要求。在北京工业大学贺玉龙和郑柯的博士论文[7，8]中则分别考虑了运行速度以及驾驶员心生理反应等因素对同向曲线间的短直线长度进行了研究。张荣洁[9]认为同向曲线之间的最小直线长度，随着曲线半径的增大而减小，当半径大于一定值 (约为600 m)后，直线最小长度稳定在220 m左右。

总而言之，目前的研究在考虑同向曲线间短直线长度时，主要以是否引起反弯错觉为判断依据，但是对于反弯错觉的界定标准又存在很大的主观性，因此对于同向曲线间的短直线长度进行定量化研究具有重要的意义。本文利用UC-win/Road软件进行不同设计条件下的工况仿真模拟，得到了在不同平面设计指标和车速情况下的行车轨迹，量化分析行车速度、圆曲线半径及同向曲线之间直线长度对同向曲线路段最大横向偏移量的影响显著性，同时对比分析同向曲线之间具有不同直线长度的同向曲线路段横线偏移值沿道路纵向分布规律，从行车轨迹角度对同向曲线路段进行综合分析。

1 同向曲线行车特性

在进行同向曲线设计时，主要考虑了短直线长度不足引起的驾驶员视觉误判和操作困难问题。在同向曲线之间插入短直线被称为“断背曲线”。“断背曲线”不仅会破坏线形的连续性，甚至会使驾驶员产生错觉，如图1所示，把线形看成两段同向弯曲的连续曲线中间插入一个反向弯曲曲线，在行车过程中，驾驶员常因未能注意到曲线半径的变化，不能及时调整方向及行驶速度而发生事故。此外，保证驾驶员操纵方向盘不感到困难的行程长度至少有6秒的行驶时间，这是因为往一个方向转动方向盘最少需要3秒。若直线长度过短，将会导致驾驶员操纵方向盘困难，引发交通事故[10]。

图1 断背曲线的错觉

车辆在曲线路段行驶时，由于受到视距不良和线性限制的原因，驾驶人员会通过不断调整车速和转向来使车辆安全通过曲线，因此车辆在通过曲线路段时很难完全沿着设计的行车道中心线进行行驶。而实际的行车轨迹也会由于车速和平面半径的不同而有所区别。邓天民等[11]的研究，根据轨迹横向偏移率的聚类结果，得到山区公路曲线路段有6种轨迹模式，具有明显的多样性特征；而且平曲线半径越小，切弯效应越大，事故风险可控，驾驶人越倾向于采用切弯方式来通过弯道，曲线路段是否发生切弯行为的临界半径值为 200 m。由于曲线的存在，大型车和小型车驶于基本型曲线时，于弯道内侧QZ断面轨迹横向偏移量最小，而于弯道外侧QZ断面轨迹横向偏移量最大，当驾驶员对连续弯道路况较为熟悉或者行车过程逐渐适应弯道频繁转向后，倾向于靠近道路中心线行驶。李晨[12]提出了车辆在通过曲线路段时主要有4种轨迹模式，并分别介绍了每一种轨迹模式所对应的条件，这4种轨迹模式分别是正常轨迹、漂移型轨迹、校正型轨迹和切弯型轨迹。一般情况而言，驾驶人会根据期望产生相应的期望速度与期望轨迹，当实际情况发生变化时，行车轨迹和速度就会做出相应调整。邢大伟[13]提出视觉作为驾驶员获取信息的主要途径，约85%以上的信息都依靠视觉获得，因此视觉感知特性直接影响到驾驶员的操作与车辆的运行状态。综上，行车轨迹能间接反映驾驶员对于路况信息的处理。

因此，为了研究车辆在通过同向曲线路段时的横向稳定性，以轨迹横向偏移值为研究对象，综合考虑车速、半径以及曲线间短直线长度的影响，本文以此为切入点，对同向曲线路段车辆进行驾驶仿真实验。通过得到的实际轨迹数据，首先分析了影响行车轨迹最大横向偏移量的影响因素以及影响强弱，其次对于横向轨迹偏移量在不同设计车速和半径下的纵向分布规律进行了总结与分析。

2 驾驶仿真实验设计

目前关于车辆行车轨迹的获取方法主要分为实车实验法、计算机仿真法和驾驶模拟仿真法等三大类。具体如下。

(1) 实车实验法：实验者驾驶车辆在选定的实验路段行驶，通过无人机摄影，路侧安置的摄像机、传感器等来捕捉车辆运行轨迹或在特定断面的横向偏移值。例如，Fitzsimmons等[14]通过路面充气管来记录曲线路段的轨迹和速度，分析了轨迹横向偏移以及切弯行为。符锌砂、林慧等[15]均采用了路侧摄像来获取轨迹偏移。

(2) 计算机仿真法：应用电子计算机实现对道路、车辆、驾驶员及环境的全面模拟，相应模型均为特定的算法或程序。常见的计算机仿真法软件有Carsim、Trucksim等。

(3) 驾驶模拟仿真法：实验者通过操纵驾驶模拟器，在搭建的虚拟实验道路上行驶，通过软件系统自带的数据记录、输出功能获取行车轨迹数据。与计算机仿真法将特定程序作为驾驶员决策模型不同，驾驶模拟仿真法是驾驶员通过操纵驾驶模拟器来对驾驶决策进行输入，主导者仍是人。常见平台如同济大学的交通行为与交通安全模拟实验平台，长安大学的六自由度汽车性能虚拟仿真实验平台、2自由度UC-win/Road运动仿真平台等。

结合上述内容，总结各方法优缺点见表1。

表1 行车轨迹获取方法对比

本研究的目的是探讨高速公路短直线路段在不同平面设计指标及行车速度下的行车轨迹特性，在现实道路上选择具有不同平面设计指标的实验路段并开展实车实验十分困难；此外，实车实验也仅能获取部分断面的轨迹横向偏移值，并存在一定的安全隐患，因此本研究放弃采用实车实验法。

对于计算机仿真法和驾驶模拟仿真法，两者在构建道路模型方面差别不大，计算机仿真法在车辆模型方面更为精确，而驾驶模拟仿真法在驾驶员决策方面更加贴近实车驾驶情况；在数据采集方面，软件系统自带的数据采集、输出功能均较为强大，基本可认为能采集任意位置的行车轨迹数据，因此均可满足实验数据采集的要求。而行车轨迹可间接反映驾驶员感知道路、环境等信息，通过大脑分析处理后，并采取相应驾驶操作的结果，该过程受驾驶员影响较大。综上，本研究采用驾驶模拟仿真方法获取行车轨迹数据。

2.1 道路模型

如图2所示，要确定一个短直线路段的平面线形，需要输入的指标包括两端的直线段长度L1和L3；第一段曲线及第二段曲线之间的直线长度L2；第一段曲线的圆曲线半径R1，及其两端的回旋线参数A11，A12；第二段曲线的圆曲线半径R2，及其两端的回旋线参数A21，A22。本研究主要探讨短直线路段圆曲线半径(图2中R1及R2)、同向曲线之间直线长度(图2中L2)以及通过短直线路段的行车速度对短直线路段行车轨迹的影响。同时采用正交实验设计实验方案。

图2 短直线路段示意图

本研究将以上三个因素均划分为三种水平。其中，通过直线路段的行车速度分别采用80 km/h、100 km/h、120 km/h，分别与高速公路常用的设计速度相对应。短直线路段的圆曲线半径分别采用800 m、1400 m、2000 m，分别与设计速度80 km/h、100 km/h、120 km/h时圆曲线半径一般值相对应。根据《公路路线设计规范》同向曲线之间直线长度小于设计速度6倍形成短直线路段， 因此本研究也将同向曲线之间的长度划分为三种水平0～2 V，2～4 V，4～6 V，同时分别取其中值1 V、3 V、5 V进行道路模型构建。因素水平划分见表2。

表2 因素水平表

同时，选用合适的正交实验表L9(34)进行实验方案设计，具体见表3。

表3 正交实验方案

除了以上三个参数外，为使车辆到达曲线路段时能够达到预定的行车速度，本研究在曲线路段两侧设置了两个直线段L1、L3，两段长度均为1 km。缓和曲线参数A11、A12、A21、A22取值则参考《公路路线设计规范》相关要求，同时兼顾超高过渡长度、最小缓和曲线长度的要求。本研究中用到的实验路段具体参数见表4。

本研究主要探讨短直线路段平面设计指标及通过短直线路段的行车速度与短直线路段行车轨迹之间的关系，因此在道路建模时道路纵断面采用直坡段，未设置竖曲线。此外，为减小纵坡对实验结果的影响，本研究道路纵坡采用0.3%，道路纵断面图如图3所示。

图3 道路纵断面参数标定

本研究道路横断面采用国内双向四车道高速公路常用横断面组成，其路幅组成为：0.75 m土路肩+3 m硬路肩+2×3.75 m行车道+0.75 m左侧路缘带+2 m中央分隔带+0.75 m左侧路缘带+2×3.75 m行车道+3 m硬路肩+0.75 m土路肩=24.5 m。本研究标准横断面如图4所示,标准断面路幅宽度24.5 m，行车道、硬路肩横坡均采用2%。应当注意，道路位于曲线路段时，会随着圆曲线半径、设计速度等的变化采用不同的超高值，本研究对道路的超高进行标定，不同路段超高取值按照《公路路线设计规范》(JTG D20—2017)进行取值，例如设计速度为80 km/h、圆曲线半径为800 m时，该路段行车道、硬路肩超高均采用4%。不同路段之间的超高过渡可通过添加Transition来进行设置，设置完成后其会在道路纵断面图中进行位置示意。某工况下UC-win/Road道路模型如图5所示。

图4 道路横断面参数标定

图5 道路模型

2.2 车辆模型

UC-win/Road车辆模型主要包括车辆3D模型及其动力学模型两部分。本研究以小型车为研究对象开展仿真实验，参考《公路工程设计标准》中对车辆宽度、轴距等相关要求，在UC-win/Road中对车辆3D模型进行参数标定，如轴距设置为2.5 m，车辆宽度设置为1.8 m等。相关参数设定如图6所示。

图6 车辆参数标定

车辆动力学方面，UC-win/Road除了可采用其自身车辆动力学外，还可采用INNOSIMULATION车辆动力学以及CarSim车辆动力学，本研究采用UC-win/Road车辆动力学。

2.3 实验方案

建立完仿真模型后，即可开展驾驶模型仿真实验。对于驾驶人的选取，本次驾驶实验由15位志愿者实际操作，在所建立的道路模型中进行无干扰的自由驾驶，平均每人驾驶次数为2次，每个工况得到约30组样本。仿真结束后，即可得到车辆行驶轨迹。志愿者由10名男性驾驶员和5名女性驾驶员组成，驾驶年龄主要是3～5年，具有相对充分的驾驶经验。根据得到的实验结果，对每组工况下的所有样本数据进行平均值计算。

本研究采用车辆重心偏移相应行车道重心线的距离分析短直线路段行车轨迹特性，而UC-win/Road驾驶模拟器输出的行车轨迹为车辆左侧轮胎至左边界的距离或右侧轮胎至右边界的距离(图7中的A或B)。因此，需要将其转化为车辆重心偏移相应行车道中心线的距离(图7中L)，以便后文分析车辆的横向偏移特性。转换公式为：

图7 L与A、B关系示意图

式中：L为车辆重心与相应行车道中心线距离，m；

A为车辆左侧轮胎至左侧边界距离，m；

B为车辆右侧轮胎至左侧边界距离，m。

根据L定义以及图7可知，L为负值时，表示车辆向右侧偏移；L为正值时，表示车辆向左侧偏移。

3 仿真结果分析

3.1 最大横向偏移值

本研究按前文所述的实验方案进行驾驶仿真实验，得到了驾驶员采用不同行车速度通过不同圆曲线半径、不同短直线长度的短直线路段时车辆的最大横向偏移值，不同实验方案下最大横向偏移值仿真结果，见表5。

表5 最大横向偏移值

续表

对正交试验结果的分析方法主要有两种，一种是极差分析(直观分析)，另一种是方差分析。极差分析原理简单，可排出影响因素的主次顺序，并确定最优水平的搭配，但无法判断考察因素对试验结果的影响是否显著，也无法确定考察因素的显著性水平；方差分析除了具有极差分析功能外，克服了极差分析的缺陷，但其分析过程较为复杂[16]。本研究需确定行车速度、圆曲线半径以及同向曲线之间直线长度对轨迹最大横向偏移量的影响是否显著，并确定相应的显著性水平，因此对正交试验结果进行方差分析。方差分析相关原理及计算方法可参考上文提到的数理统计，同时也可借用SPSS、MATLAB、MINITAB等统计工具进行方差分析。

短直线路段行车轨迹最大横向偏移值方差分析结果见表6。

表6 方差分析结果

当给定显著水平α=0.05时，F分布上侧分位数，F0.05(2,2)=19.000。由表6可知，因素A、C对应F值分别为133.619和124.373，远大于F0.05(2,2)=19.000，说明圆曲线半径，以及通过短直线路段的行车速度对短直线路段行车轨迹最大横向偏移值都是非常显著的。文献[12]研究结果与本文研究结果一致，对于短直线路段而言，圆曲线半径以及通过短直线路段的行车速度仍然是影响行车轨迹最大横向偏移值的两个关键因素。根据表6可知，因素B对应F值为1.922，小于F0.05(2,2)=19.000，说明同向曲线间直线长度对短直线路段行车轨迹横向偏移值不显著，从道路几何设计指标角度来说，其不是影响短直线路段行车轨迹最大横向偏移值的关键因素。

3.2 横向偏移值沿道路纵向分布

在圆曲线半径一定的条件下，同向圆曲线之间采用不同的短直线从而形成不同的短直线路段。本研究以设计速度80 km/h，圆曲线半径采用800 m条件下不同的短直线路段为例，对短直线路段最大横向偏移值的位置进行分析。仿真实验时，通过短直线路段的行车速度均采用80 km/h，同向曲线间的直线长度分别取设计速度的1倍(1V)、3倍(3V)、倍(5V)，即80 m、240 m和500 m。

本研究在分析短直线路段行车轨迹最大横向偏移值位置时，为获得一个参照标准，获取了基本型曲线路段的行车轨迹数据。该基本型曲线圆曲线半径、转角、缓和曲线参数及长度与短直线路段保持一致。

通过驾驶模拟获取了驾驶员采用80 km/h行车速度通过基本型曲线路段(即直线+缓和曲线+圆曲线+缓和曲线+直线)时车辆的行车轨迹，其横向偏移值与桩号的关系如图8所示。

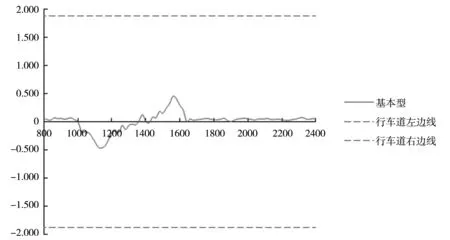
图8 基本型曲线行车轨迹(单位：m)

结合前文可知，图7所采用的实验路段ZH点桩号为K1+000，HY点桩号为K1+100，YH点桩号为K1+555，HZ点桩号为K1+655。由图7可知，车辆进入曲线段时，行车轨迹表现为向曲线内侧偏移(向右侧偏移)，车辆驶出曲线路段时，行车轨迹表现为向曲线外侧偏移(向左侧偏移)。这与文献[17]研究结果“车辆右转弯时，入弯至出弯呈现右偏—左偏”相一致。同时，由图7可以看出向曲线内侧的横向偏移量最大值发生在K1+150附近，向外侧偏移的横向偏移量最大值发生在K1+550附近，即分别发生在HY和YH点附近。

通过驾驶模拟获取了驾驶员采用80 km/h行车速度通过采用不同直线长度(80 m、240 m、400 m)的短直线路段时车辆的行车轨迹，其横向偏移值与桩号的关系如图9所示。

图9 横向偏移值(单位：m)

由图8可知，同向曲线之间分别采用80 m、240 m和400 m所形成的短直线路段其行车轨迹最大横向偏移值均约为0.5 m，同时与图7中基本型曲线路段行车轨迹最大横向偏移值也较为接近，进一步说明了同向曲线之间的直线长度不是影响短直线路段行车轨迹最大横向偏移值的主要因素。

同时，由图8还可发现，当同向曲线之间直线长度较短时(图8中的1V)，行车轨迹横向偏移值随桩号的变化情况与基本型曲线较为接近，这说明当同向曲线之间直线长度较小时，其往往被驾驶员误以为是曲线路段，驾驶员即使行驶在短直线上也不会将方向盘回正，而是与基本型曲线路段类似，采用一定的方向盘转角来通过短直线路段。随着同向曲线之间直线长度的增加(图8中的3V)，驶入第一段曲线和驶出第二段曲线时行车轨迹偏移值随桩号变化情况与基本型曲线类似，驾驶员均有向曲线内侧或外侧偏移的倾向，而由第一段曲线驶入短直线(驶出第一段曲线)和由短直线驶入第二段曲线(驶入第二段曲线)时，驾驶员有向曲线内侧或曲线外侧偏移的倾向，但不明显，这说明驾驶员开始意识到同向曲线之间的短直线，并具有将方向盘回正的意识，但因直线长度较短，其没有充足时间来完成操作。随着同向曲线之间直线长度的进一步增加(图8中的5V)，驶入、驶出第一段曲线，或驶入、驶出第二段曲线时行车轨迹偏移值随桩号变化情况分别与基本型曲线类似，驾驶员在驶入驶出第一段、第二段曲线时行车轨迹向内侧、外侧偏移的倾向均较为明显，说明驾驶员已经能够较为清楚地意识到同向曲线之间的直线路段，并有较为充裕的时间来将方向盘回正，完成驾驶操作。

4 结 论

(1) 分析了同向曲线路段最大横向偏移值与行车速度、圆曲线半径及同向曲线之间长度之间的相关性，发现圆曲线半径、行车速度对其影响较为显著，而同向曲线之间直线长度对其影响不显著。

(2) 在80 km/h行车速度、圆曲线半径采用800 m条件下，对比分析了同向曲线之间长度分别采用1V、3V、5V所构成的同向曲线路段行车轨迹横向偏移值沿道路纵向的分布规律，发现同向曲线之间直线长度的变化不影响横向偏移量的峰值(最大横向偏移量)，但对横向最大横向偏移量出现的位置具有显著影响。

(3) 同向曲线之间长度较短时(1V)，其行车轨迹纵向变化规律与基本型曲线类似，仅在驶入第一段曲线及驶出第二段曲线时有较为明显的横向偏移；当同向曲线之间长度较大时(5V)，在驶入驶出第一段曲线，驶入驶出第二段曲线时均有较为明显的横向偏移；而当同向曲线之间长度适中时(3V)，在驶出第一段曲线及驶入第二段曲线时有一定的横向偏移，但不明显。

(4) 仅分析了同向曲线路段最大行车轨迹偏移值与圆曲线半径、同向曲线之间直线长度、行车速度之间的相关性，后续研究中可建立同向曲线路段最大行车轨迹偏移值的预测模型。

(5) 在建立道路模型时，第一段曲线半径R1与第二段曲线半径R2采用了同一半径，同时第一段曲线缓和曲线参数A11、A12与第二段曲线缓和曲线参数A21、A22均相等，后续可研究参数以上参数取值的变化对同向曲线路段行车轨迹的影响。