基于路面估计的车辆避撞控制策略研究

李文礼,赵 瑞,廖达明,钱 洪,李亚娟

(1.重庆理工大学 车辆零部件先进制造技术教育部重点实验室,重庆 400054;2.重庆理工清研凌创测控科技有限公司,重庆 400054;3.重庆青山工业有限责任公司,重庆 402761)

车辆的避撞功能是智能车辆安全系统的重要组成部分,现有的避撞控制策略很少考虑变路面工况的影响,无法实现对变路面工况的动态自适应控制[1]。传统的避撞控制策略在面对变路面时会直接开启防抱死制动系统ABS进行控制,而这大大降低了乘员的舒适性。获取路面附着系数能实现车辆更高的控制精度,是在保证安全性的前提下提高舒适性的有效途径。目前,路面估计方法分为3种:第1种是通过安装在轮胎上的传感器直接进行测量估计,如声音传感器[2]、光学传感器[3]和雷达等;第2种是利用车辆动力学模型和轮胎模型进行附着系数估计[4],用常见的车载传感器获取车辆行驶状态信息并应用贝叶斯估计方法进行估计[5];第3种是基于滑移率[6]的方法。余卓平等[7]利用激光雷达对路面进行估计,成本较高,参考路面数据难以获取。杨秀建等[8]使用最小二乘法和滑移率进行估计,实现实时路面附着系数估计,然而滑移率曲线估算的最大附着系数只能在轮胎附着力较小和滑移率较小的条件下实现。Berkeley安全碰撞策略首次在避撞控制中考虑路面影响[9]。蒋春文[10]使用递归最小二乘法估计附着系数,在考虑坡度的基础上提出了将最大制动减速度应用于安全距离公式和碰撞时间相结合的多级碰撞预警系统中,然而并没有考虑制动时的舒适性。李霖等[11]提出一种两级预警两级制动的避撞策略,然而并没有考虑路面附着系数的影响。周兵等[12]考虑路面状况和量测噪声干扰,建立了路面状况、车速和最大减速度的模糊关系以提升碰撞危险的评估效果,然而需要提前获取路面情况。汪等[13]设计了适应不同路面附着条件和驾乘人员舒适度的转向制动联合避撞策略。较多的避撞控制通过多级制动优化整个制动过程,而制动分级越多,制动策略越复杂。考虑到制动过程中的舒适性,均在舒适性减速度的区间内选择固定的制动减速度,若当前制动策略切换时,期望制动减速度实现跳变,则会产生较大的冲击度。

为了提高车辆制动的安全性和舒适性,提出一种基于路面附着系数的车辆主动避撞控制策略。首先,使用容积卡尔曼滤波估计车辆状态和路面附着系数;然后,在估计的路面附着系数的基础上,建立基于路面附着系数的安全距离模型。考虑制动时驾乘人员的舒适性,使用压力控制以避免制动分级产生的阶跃,直接对制动压力进行约束优化,以增强车辆在变附着系数路面的安全性和舒适性。

1 车辆状态及路面附着系数估计

为了实现更高的估计精度和较小的计算量,采用四自由度车辆模型和参数较少的Dugoff轮胎模型来计算轮胎力。

1.1 四自由度车辆动力学模型

车辆模型是一个有纵向、侧向、横摆和侧倾4个自由度的非线性系统,模型如图1所示。

车辆动力学方程式可描述为

(1)

(2)

式中:m为整车质量;ms为簧载质量;Iz为转动惯量;a为质心至前轴距离;b为质心至后轴距离;hs为质心高度;g为重力加速度;vx为纵向车速;vy为侧向车速;vcog为车辆合速度;δij为车轮转角;r为横摆角速度;φ为车身侧倾角;ax为纵向加速度;ay为侧向加速度;βφ为质心侧偏角;κφ为侧倾角刚度;αij为车轮侧偏角;λij为车轮滑移率;vij为车轮中心速度;tf为前轮轮距;tr为后轮轮距;Fx_ij为轮胎纵向力;Fy_ij为轮胎侧向力;Fz_ij为车轮垂直载荷;i为前轮f或后轮r;j为左轮l或右轮r。

1.2 Dugoff轮胎模型

Dugoff轮胎模型是理论模型中的稳态模型,具有路面附着系数参数,能够模拟轮胎的稳态运动过程。Dugoff轮胎模型的计算式为

(3)

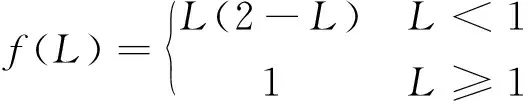
(4)

(5)

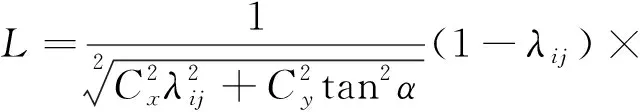
(6)

式中:Cy为轮胎侧偏刚度;Cx为轮胎纵向刚度;Re为车轮滚动半径;ωij为轮胎的转速;ε为速度增益系数。

1.3 基于容积卡尔曼滤波的车辆状态估计与附着系数估计

将车辆行驶状态估计[14]与路面附着系数估计结合起来,应用容积卡尔曼滤波算法对车辆状态与路面附着系数进行估计,具体估计过程如图2所示。

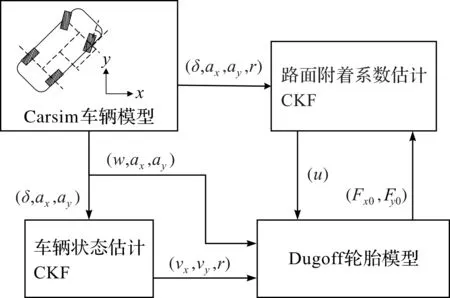
图2 车辆状态估计和路面附着系数估计结构图Fig.2 Structure diagram of vehicle state estimation and roadadhesion coefficient estimation

建立系统的状态方程与量测方程,即

(7)

式中:状态变量X1=[vx,vy,r,ax,ay,Γ];参数变量X2=[μfl,μfr,μrl,μrr]。

车辆行驶状态估计器的测量输出和路面附着系数估计器的测量输出和估计器控制输入为

Z1=Z2=Z=[ax,ay,r]

Uk=[δ,ωfl,ωfr,ωrl,ωrr]

路面附着系数估计状态方程为

(8)

其中:

为避免求取协方差矩阵中容易出现奇异值导致矩阵非正定的问题,使用SVD分解代替传统的cholesky分解。仿真使用的参数如表1所示,仿真结果如图3,4所示。

表1 车辆模型参数

图3 不同路面附着系数不同车轮估计值Fig.3 Estimated values of different wheel adhesion coefficients on different roads

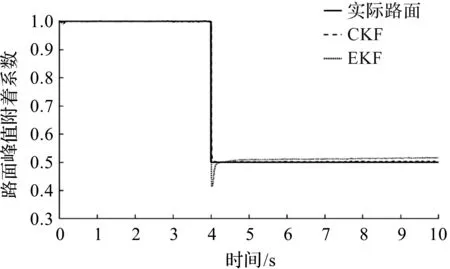
图4 4个车轮路面附着系数估计平均值Fig.4 Estimated average value of road adhesion coefficientfor four wheels

通过图3可以看出:车辆对恒定的路面附着系数估计误差较小,误差约为6%,而对变化的路面附着系数估计误差较大,尤其是单个车轮的估计值,误差达到了20%。由于车轮的计算公式使用的是同样的公式,计算较为简单,其中的数值基本是对称的,因此使用4个车轮估计路面附着系数的平均值。而此时使用容积卡尔曼滤波(CKF)在路面变化时产生的误差要明显小于使用扩展卡尔曼滤波(EKF)产生的误差。

2 基于压力控制的主动避撞控制策略

基于压力控制的主动避撞控制策略首先通过上述估计的路面附着系数和车速等信息,计算出车辆制动所需要的制动压力;其次结合车辆的安全状态决定车辆制动压力的增加与减少;再次对压力进行压力规划,使用多项式路径来平滑压力曲线,进行约束优化[15],得到理想的制动压力;最后使用模型预测控制器作为下位控制器,根据得到的理想制动压力进行舒适性的约束,从而将制动压力返回给车辆,形成一个闭环控制。避撞控制策略结构图如图5所示。

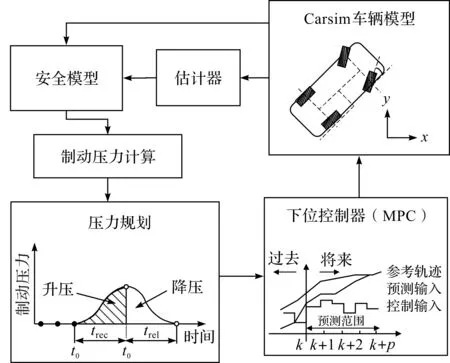
图5 避撞控制策略结构图Fig.5 Collision avoidance control strategy structure diagram

2.1 安全距离模型

车辆的停车距离取决于制动初速度、反应时间和路面附着系数,即

(9)

式中:T1为减速时间;T2为延迟时间,一般为0.05～0.20 s;u0为制动初速度。

对路面附着系数的估计值是理想的路面峰值附着系数,引入附着系数利用率来模拟实际道路上的路面附着系数。路面附着系数利用率为

(10)

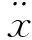
当相对减速度达到最大,即拥有最大减速度时,附着系数利用率变成质量系数,其数值与驾驶员的操作无关。为保证车轮不抱死,相关法规要求质量系数要大于0.75。最短停车距离可表示为

(11)

式中Δv为前后车相对速度。

鉴于不同年龄的驾驶员有不同的反应时间,反应时间主要分为3类:反射时间、判断时间和行动时间。反射时间为0.44～0.52 s,判断时间为0.15～0.25 s,行动时间为0.15～0.40 s。而不同年龄段的人反应时间为0.74～1.17 s[16]。在设定最小制动安全距离时应加入驾驶员的反应时间,通过驾驶员反应时间的不同,设定一个最大制动安全距离和最小制动安全距离,即

0.74u0+S

(12)

1.17u0+S

(13)

安全距离要考虑驾驶员心理安全距离S,心理安全距离为2～5 m,取3 m。通过得到不同驾驶员的反应时间所区分的最大安全距离和最小安全距离,形成了多级的安全制动距离,结果如图6所示。

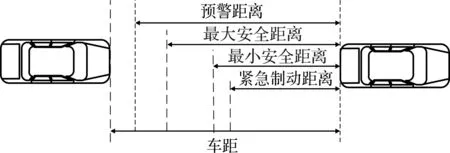
图6 车辆分级制动Fig.6 Vehicle graded braking

将简化后的安全距离模型用于计算TTC阈值,即

(14)

式中:TTCemerg为车辆采取紧急制动的碰撞时间;TTCbrake为车辆采取部分制动的碰撞时间;u为车速。

为了提高TTC的精度,TTC可表示为

(15)

将TTC与TTCbrake和TTCemerg进行比较得到3种模式信号,即

(16)

2.2 制动压力计算

车轮的力矩平衡方程为

(17)

∑T=Ts-Tb-Trr-rFx

(18)

式中:Ts为发动机转矩;Tb为制动力矩;Trr为滚动阻力矩;rFx为轮胎纵向力扭矩。

制动系统压力的形成与液压回路、比例阀有关,建立的模型为

Tb=GP

(19)

式中:Tb为制动器制动力矩,Nm;G为制动器制动系数,Nm/kPa;P为制动器气液压力,kPa。

2.2.1 制动压力规划

当车辆需要制动时,车辆会尽可能快地增大或减小制动压力,而制动压力变化过快,会导致车辆在制动开始和结束时有一个抬升量和下沉量。因此,对计算的制动压力进行约束,以尽量避免这种情况的发生。制动压力变化示意图如图7所示。

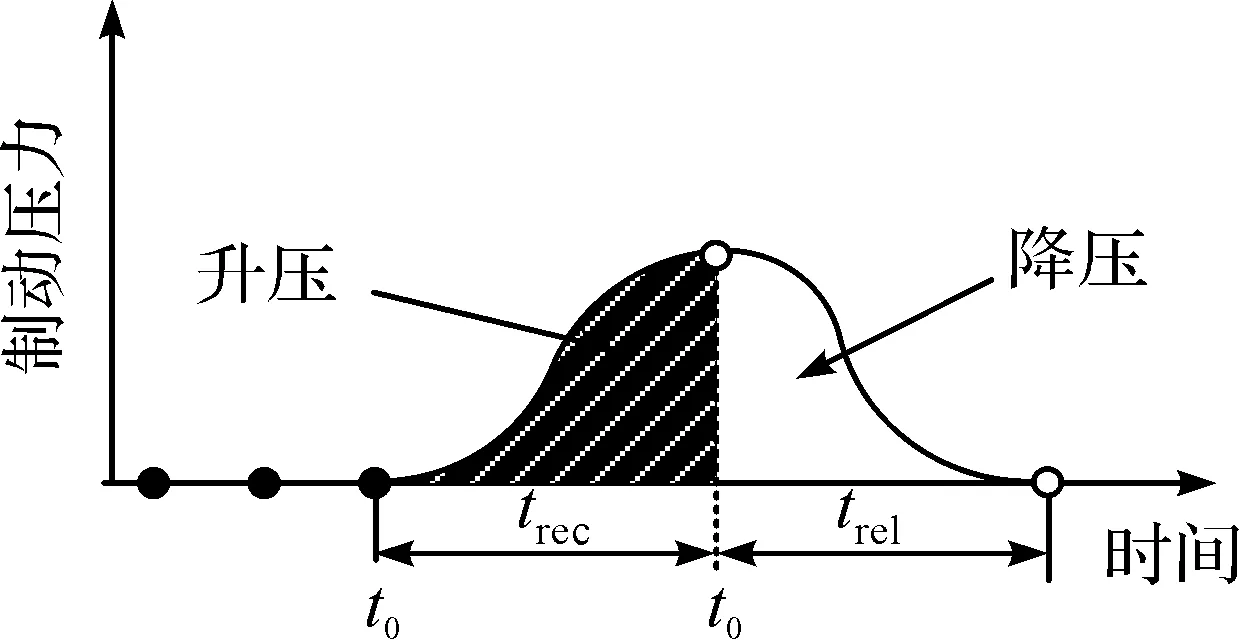
图7 制动压力变化示意图Fig.7 Schematic diagram of brake pressure change

将制动压力的变化简化为一个三次函数,即

P(t)=c0t3+c1t2+c2t+c3t0≤t≤t0+Δtrec

(20)

将信号触发时的压力作为初值,计算的制动压力作为终值。升压过程的约束条件[17]为

(21)

降压过程的约束条件为

(22)

2.2.2 制动压力控制

所规划的制动压力使用阶段性的约束,在每个阶段依然会存在小幅度的阶跃。单位时间内制动压力的变化越小,车辆产生的制动力矩也就越平稳,车辆产生的减速度和冲击度也会越小。使用模型预测控制[18](MPC)能“快速”“平稳”地跟随制动压力轨迹曲线,同时加入约束可以减少制动压力产生阶跃,以提高驾乘人员的乘坐舒适性。

制动压力和制动力矩在一定范围内成正比例关系,因此制动系统可以使用一个一阶惯性系统来表示,即

(23)

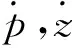
(24)

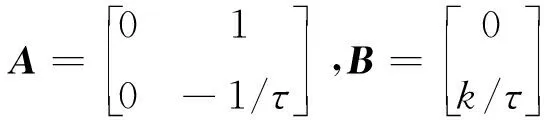
(25)

式中:x=[pz]T为系统状态向量;u=zdes为系统控制输入。将连续方程离散化,即

x(k+1)=Akx(k)+Bku(k)

(26)

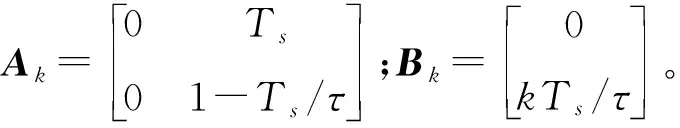
系统的输出方程为

y(k)=Cx(k),C=[1 0]

(27)

滚动优化表示为

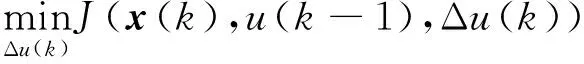
(28)

构造代价函数J表示为

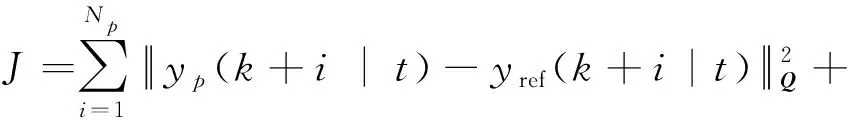
(29)

式中:Q为误差惩罚项权重矩阵;R为控制量增量惩罚项权重矩阵。在约束条件下求解函数,使实际压力与参考压力的差值达到最小,即

(30)

3 仿真与分析

基于Simulink/Carsim进行仿真试验,对建立的避撞策略进行仿真和分析。仿真设定最大舒适性减速度为-6 m/s2,设定两车初始距离为10 m,前车以5 m/s的速度前进,后车以10 m/s的速度接近前车。为了降低驱动力调节对车辆制动产生的影响,使用恒定驱动转矩,因此车辆开始时会保持恒定的减速度,而且制动产生速度波动。

在控制策略中对制动压力进行规划和约束,当车辆产生制动时,制动压力的跳跃变化非常大。考虑在部分制动的过程中,车辆没有条件触发紧急制动就会处于较为安全的状态。此时考虑车辆的制动舒适性,车辆计算的制动压力产生的波动依然很大,使用模型预测控制(MPC)对制动压力进行约束可以降低制动压力的变化。使用MPC所产生的压力波动要远小于使用比例积分微分(PID)控制的波动(图8)。由于考虑了舒适性,加入压力变化率约束导致MPC的控制响应速度变慢,产生了约0.1 s的滞后,而PID控制虽然跟随效果优于MPC,但是也产生了较大的超调量。

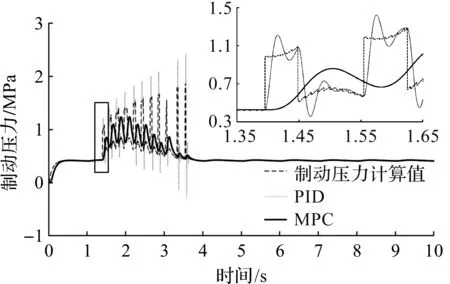
图8 制动压力曲线Fig.8 Brake pressure curve

制动压力曲线的跟随主要是用于部分制动工况,其对制动压力准确跟随的需求低于制动压力变化幅度的需求,因此需要制动压力有一定的跟随性能和较为平缓的变化幅度,这样才能提高驾乘的舒适性。约束制动压力能够降低冲击度,使用MPC控制制动压力可以有效降低车辆在制动过程中产生的冲击度,其效果优于使用PID控制,尤其是路面附着系数发生改变时,MPC控制效果尤为显著,如图9,10所示。

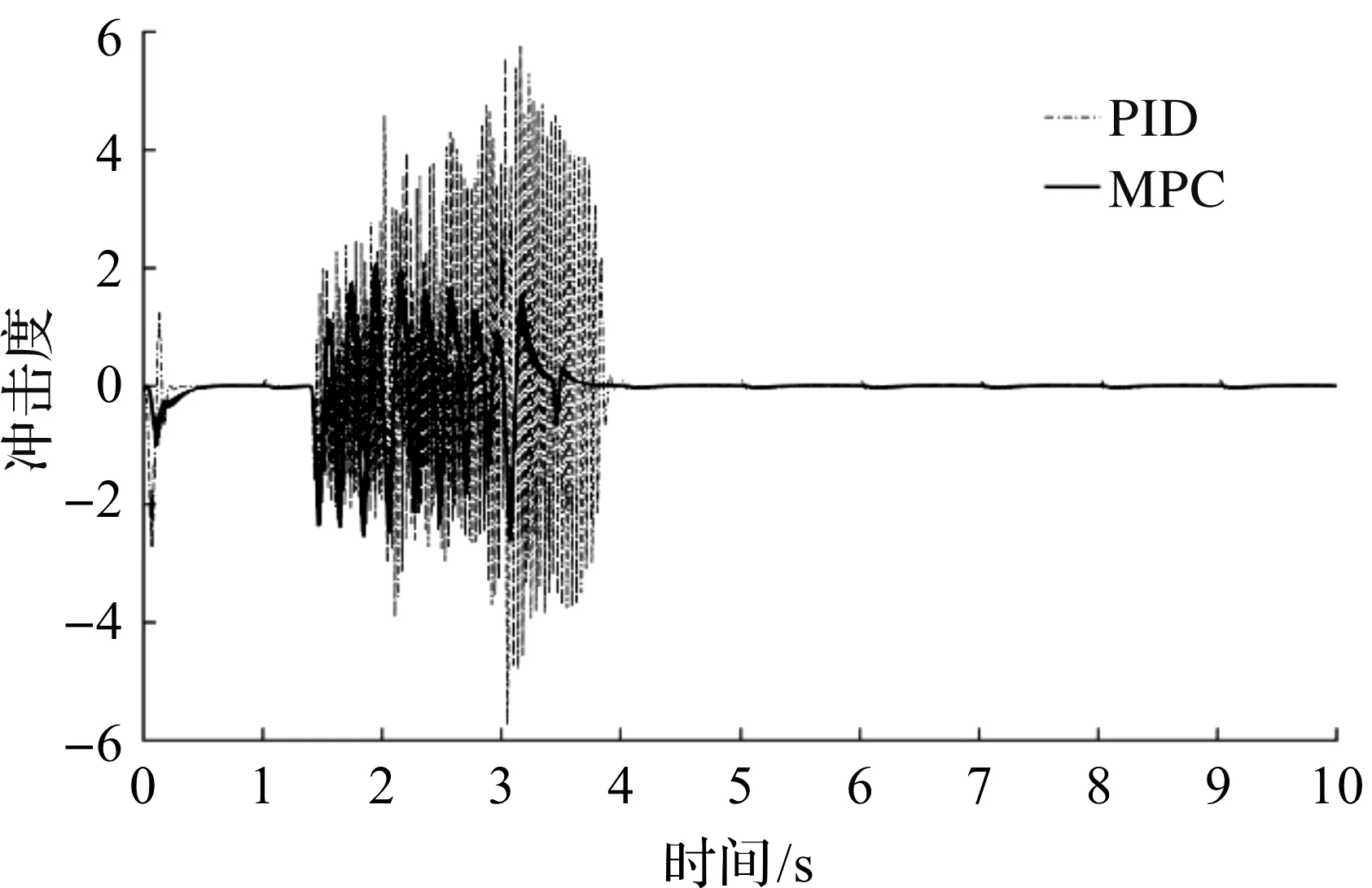
图9 定路面附着系数冲击度曲线Fig.9 Jerk curve with constant adhesion coefficient

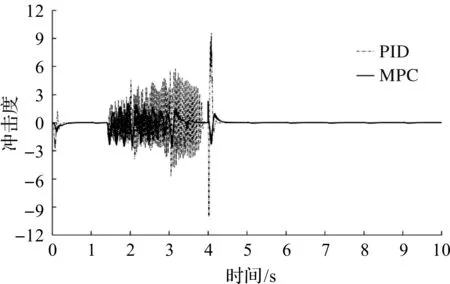
图10 变路面附着系数冲击度曲线Fig.10 Jerk curve with variable adhesion coefficient

路面附着系数在第4秒时发生突变,如图4所示。图11,12显示车辆在路面附着系数变化后,车速有较为明显的降低。通常车辆在附着系数减小时会保持上一时刻的车速,因此车速会高于原有车速。本策略在制动过程中估计到路面变化,会提高制动压力或者减小制动压力,以保持原有的制动状态。车辆的制动使车辆的相对距离始终大于4 m,其中包含驾驶员心理安全距离和驾驶员的反应延迟导致的距离,距离过大主要为了避免因路面变化导致碰撞的产生。

图11 车速Fig.11 Vehicle speed

图12 相对距离Fig.12 Relative distance

图13为车辆在定路面和变路面的制动减速度图,当路面附着系数减小后,车辆的制动减速度瞬间减小,而车辆处于一种危险状态,车辆增加制动压力,提高车辆的制动力,增大制动减速度。车辆瞬间的制动减速度变化较大,主要是为了提高安全性,当车辆逐渐处于安全状态,车辆的制动减速度平缓降低以提高驾乘的舒适性。

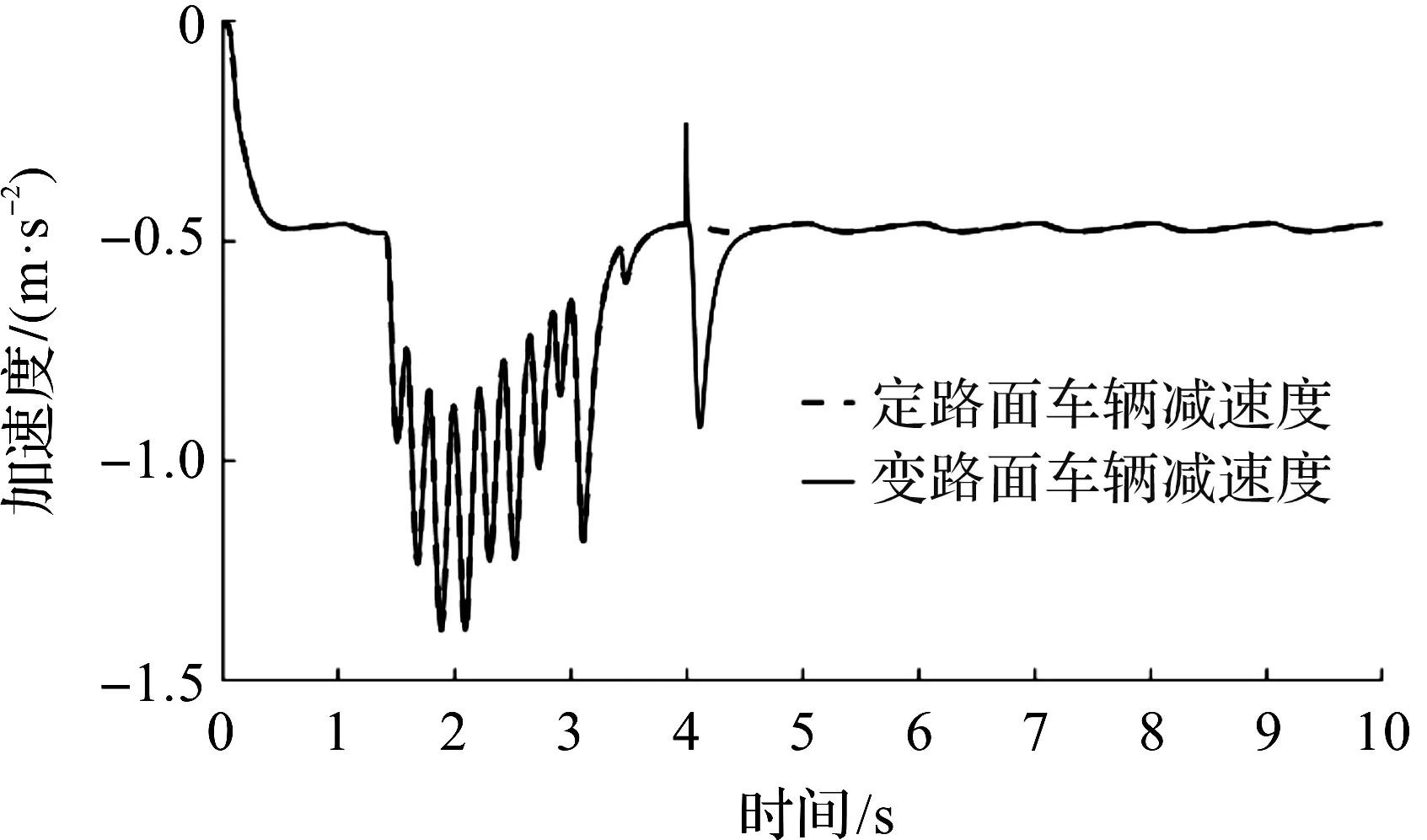
图13 加速度曲线Fig.13 Acceleration curve

由图14,15可知:车辆在1.4 s处开始采取制动,总制动时长达到2 s。由图14可知:在建立的避撞策略中,当TTC值到达阈值后,车辆开始采取制动,以脱离危险状态,由于是部分制动,因此在2 s内反复执行部分制动操作,最终脱离TTC的预警状态。当路面附着系数减小后,车辆的TTC值瞬间减小,车辆的部分制动提供的制动力瞬间增大,当TTC值脱离危险状态后,制动力恢复到原状态下。

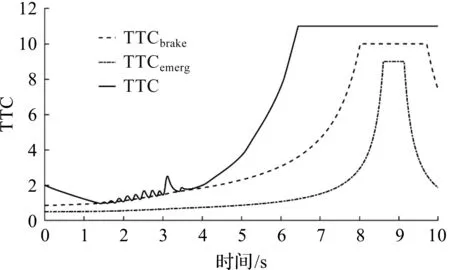
图14 定路面附着系数TTC曲线Fig.14 Time to collision curvewith constant adhesion coefficient

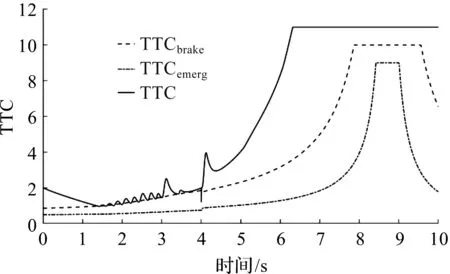
图15 变路面附着系数TTC曲线Fig.15 Time to collision curvewith variableadhesion coefficient

4 结 论

为了提高车辆在变路面工况下的安全性,提出了一种基于路面附着系数估计的避撞控制策略,使用容积卡尔曼滤波估计路面附着系数,建立了基于路面附着系数的安全制动距离模型。为提高车辆制动时的舒适性,对制动压力进行约束优化,使用模型预测控制作为控制器。结果表明容积卡尔曼的估计精度满足避撞策略的精度要求。约束优化后的制动压力配合模型预测控制能显著减小制动压力突变带来的冲击度,同时压力控制使车辆在面对变附着系数路面的工况时有很快的反应速度,根据估计的路面附着系数提出的避撞策略能够实现车辆安全避撞控制。

本文得到了重庆理工大学研究生创新资助项目(clgycx20202021)的资助。