单双向振动条件下饱和软黏土动力特性研究

李 磊,梁 超,郑 昌,昌志峰,蒋耀晨

(1.浙江交工集团股份有限公司,浙江 杭州 310051;2.浙江工业大学 土木工程学院,浙江 杭州 310023)

软黏土是指在滨海区域、沼泽地区和三角洲地带等水源充沛且水流缓慢的区域,土体经过各种生物化学反应后自然沉降形成的细粒软黏性土,其具有压缩性高、含水率高、抗剪强度低、孔隙比大和渗透性差等特点,工程性质极为不良。软黏土在我国沿海地区较为常见,随着沿海地区的高速发展,高速公路、铁路及机场等基建工程愈发密集,海上平台、人工岛等近海工程愈发多见,以上设施长期受交通荷载、波浪荷载和风荷载等动荷载作用,又多建于深厚软黏土土层之上,因此对软黏土动力特性的研究十分必要。

近年来,对饱和软黏土的动力特性试验研究逐渐增多。基于现有研究成果,循环加载下饱和细粒软黏土土体刚度随着循环圈数的增加而逐渐衰减。基于Idriss等[1]的软化指数模型,Matsui等[2]、Yasuhara等[3]、黄娟等[4-5]、周建等[6]和王军等[7]对该模型进行了考虑动应力幅值和循环圈数的修正。基于Hardin-Drnevich的表达式[8],张勇等[9]提出了含固结压力、动应力幅值和循环圈数等变量的动骨干曲线模型。Polito等[10]认为不同波形对能量耗散-孔压影响关系不大。目前,国内外学者主要关注的还是单向振动模式的循环荷载作用,如交通荷载等。事实上双向振动模式在工程中也较为常见,如波浪荷载等。双向振动与单向振动两种荷载作用存在不同[11],目前针对两者的比较研究还较为少见。王常晶等[12]认为单双向振动条件下萧山软黏土最小极限循环强度可视作一致。黄博等[13]对单双向振动条件下的饱和砂动力特性展开研究,提出当土样在较小圈数下被破坏时,单双向振动模式对试样动力特性影响较小,两者可视为等效,而在较大圈数下,两者动力特性差异明显。目前,针对饱和软黏土的单双向振动对比试验研究鲜有报道,因此笔者开展大周数单双向振动条件下饱和细粒软黏土循环三轴试验研究,主要考虑振动模式、循环圈数及动应力幅值等因素对细粒软黏土动力特性的影响,并建立考虑振动模式和循环圈数的软黏土动骨干曲线模型。

1 饱和软黏土动三轴实验

1.1 试验土样

试验所用土样为温州软黏土。温州位于我国东南,毗邻东海,是我国典型的沿海城市。温州大部分地区地质层多被深厚淤泥质软黏土层占据,厚达20～30 m,是典型的软黏土。由于温州地区在历史上未遭遇过剧烈的海平面升降或严重的地表侵蚀,一般认为天然温州软黏土为正常固结土。本研究中所用土样来自温州地区一个深度约10 m的基坑底部。由于重塑土具有较为可靠的可重复性和均匀性,试验结果可信度较高,本试验土样均采用重塑土,该重塑土制备采取泥浆加压固结法,具体步骤:1) 将试验所需用土放入烘箱烘干,先用粉碎机将烘干的土块碎成小颗粒,再用研磨机碾磨成粉;2) 根据1.2倍液限算出所需的土粉和水,称取定量的干土粉和水混合,用搅拌器搅拌均匀;3) 将泥浆倒入固结仪中,对其进行12.5,25,50,100 kPa的逐级加载,每一级加载后,待土样压缩值基本稳定后(以压缩值变化率小于2 mm/d为稳定)再施加下一级荷载,最后一级荷载加载时间延长一周,以待土样完成主固结。经室内试验,重塑土的基本物理特性如表1所示。

1.2 试验装置及试验步骤

试验装置:为了进行复杂应力路径下饱和细粒软黏土的静动力特性试验研究,笔者所采用的试验仪器为英国GDS公司(GDS Instruments,London)生产的电机伺服动三轴试验系统(图1)。该设备具有高精度、高控制力以及可进行循环加载试验的特点。

图1 电机伺服动三轴试验系统Fig.1 Motor servo triaxial testing system

土动力特性室内试验常用的方法有动三轴试验,主要适用于土在较大动应变幅(ε(γ)>10-4)时土动力特性的测试,试验步骤:1) 根据土工试验规程将重塑土样制成直径50 mm、高100 mm的标准圆柱体,周围贴上滤纸条,以增加排水通道;2) 将切好的土样装入GDS动三轴压力室反压饱和24 h,反压采用300 kPa,有效围压20 kPa,试验土样饱和度均可达到98%以上;3) 施加设定的围压完成固结。

试验分为2个部分:第1部分为单向振动加载试验,该试验部分动应力幅值σa分别为20,30,50 kPa;第2部分为双向振动加载试验,该试验部分动应力幅值σa分别为10,20,30,50 kPa,试验加载频率均为0.1 Hz。试验加载方式如图2所示,其中:OAB段表示饱和阶段;BCD段表示等压固结阶段;CD段表示对应固结围压值(本研究固结围压p′=100 kPa);DE段表示动力加载阶段,单向振动加载时为压缩波,双向振动加载时为正弦波。双向振动下动应力σd=2σa,而在单向振动下动应力σd=σa。具体试验方案见表2。

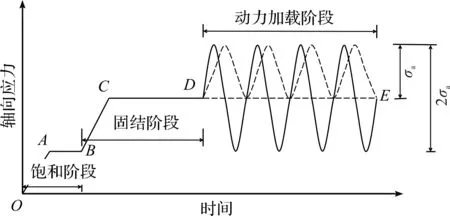
图2 典型试验加载过程Fig.2 Typical loading process

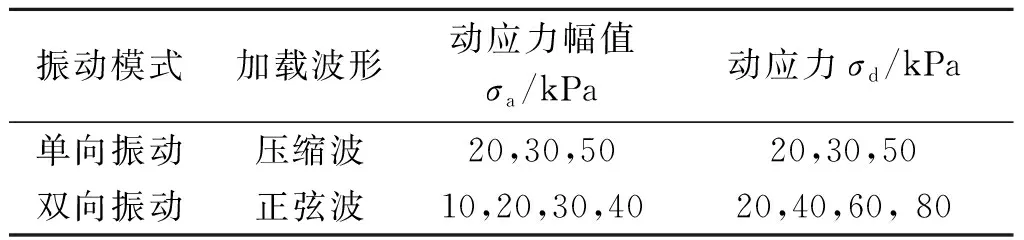
表2 动三轴试验方案

2 试验结果与分析

2.1 孔压与应变发展

图3为单双向振动条件下的孔压时程曲线。图3(a)为饱和土样在不同应力水平的双向振动荷载下孔压时程曲线,由图3(a)可知:当应力水平较小时(σd分别为20,40 kPa),孔压在较短时间内迅速完成累积,之后缓慢增长并趋于平稳;当应力水平较高时(σd=60 kPa),孔压在早期快速累积然后持续增长,当应力水平足够大时(σd=80 kPa),孔压增长极快,土样在循环圈数N=100时发生破坏。图3(b)为饱和土样在不同应力水平的单向振动荷载下孔压时程曲线,与双向振动状态下的发展模式类似,在低应力状态下,单双向振动状态下的孔压极为相近,单向振动孔压略大于双向振动。

图3 单双向振动状态下孔压时程曲线Fig.3 Development of pore pressure under one-way and two-way cyclic loading

图4为单双向振动下N=1 000时的孔压与应力水平关系曲线。图4(a)为孔压与动应力的关系曲线,在相同的动应力下,单向振动的孔压比双向振动大;图4(b)为孔压与动应力幅值的关系曲线,在相同的动应力幅值下,孔压的结果则与上述结果刚好相反。结果表明不同的振动模式对孔压的累积有显著影响。

图4 单双向振动下典型圈数孔压对比Fig.4 Development of pore pressure under one-way and two-way cyclic loading

图5为单双向振动条件下的动应变时程曲线。图5(a,b)分别为饱和土样在不同应力水平的双向和单向振动荷载下动应变时程曲线。图5(a)中,在低应力水平下,土体迅速达到安定状态,循环圈数对土体形变累积影响很小。当σa=10 kPa时,动应变εd为0.034 7%,随着圈数增加,动应变几乎没有增长。随着应力增大,循环荷载对土体扰动加剧,当应力水平超过某一临界值,如当σa=40 kPa时,土样在短时间内发生疲劳破坏。图5(b)中,土样均处于安定状态,且随动应力幅值逐渐增加,土样应变对应增大。当σa=50 kPa时,土样仍未破坏。说明振动模式对土样的应变发展有显著影响。对比图5(a,b)可知:在相同动应力幅值下,双向振动状态下的动应变比单向振动状态下的动应变大,如在动应力幅值均为20 kPa时,双向条件下的动应变是单向振动条件下的2.04倍。

图5 单双向振动状态下动应变时程曲线Fig.5 Development of dynamic strain under one-way and two-way cyclic loading

图6为单双向振动下N=100时的动应变与应力的关系曲线。图6(a)为动应变与动应力的关系,在相同的动应力下,单向振动的动应变比双向振动大;图6(b)为动应变与应力幅值的关系曲线,在相同应力幅值下,单向振动下的动应变明显比双向振动大。结果表明不同的振动模式对土体的应变发展有显著影响。

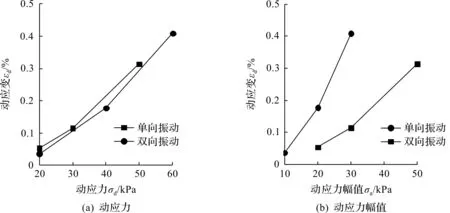
图6 单双向振动下典型圈数动应变比较Fig.6 Comparison of dynamic strains under one-way and two-way cyclic loading at typical cycle number

2.2 应力—应变关系

安定是指结构体在某一特定的循环荷载下,产生的塑性变形在有限的循环次数后稳定下来,且在安全界限内,结构体不会发生破坏[14]。在弹塑性安定状态时,动应力—动应变关系曲线可基本看为一个封闭且中心对称的滞回圈,称为滞回曲线。

图7为在典型圈数下的滞回圈对比,图中Ed和E′d分别为单向与双向振动下的滞回圈斜率。单向振动状态下滞回圈呈狭长的纺锤形,且滞回圈的面积随着循环圈数的增加逐渐减小,而双向振动状态下的滞回圈呈现明显的棘轮效应,随着荷载作用次数的增加,塑性变形越来越大,棘轮效应愈加明显,滞回圈面积也逐渐增大。此外,由于单向振动条件下试样处于弹塑性安定状态,随着循环荷载的增加,孔压与累积应变几乎不再增加,滞回圈重合,滞回圈的斜率无明显变化,土样的动模量几乎不变,双向振动状态下滞回圈的斜率随振动圈数的增加而减小,与图5中应变时程曲线结果相符。在循环加荷载初期滞回圈比较陡峭,随着圈数的增加,滞回圈的斜率逐渐降低,这种情况体现了土体在循环荷载作用下的刚度软化性。

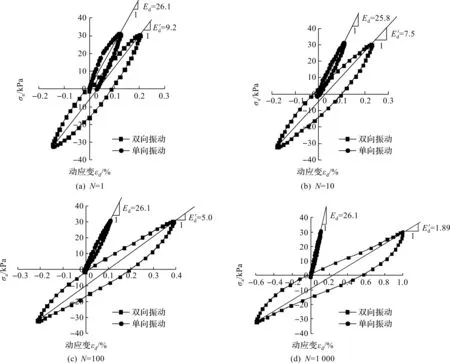
图7 典型圈数下σa=30 kPa时单双向振动条件下滞回圈对比Fig.7 Comparison of hysteretic loops under one-way and two-way cyclic loading at σa=30 kPa at typical cycle number

比较各典型振次下的单双向振动条件下滞回圈可以发现:在相同加载圈数和相同应力幅值下,单向振动条件下的滞回圈斜率大于双向振动条件下的滞回圈斜率,即单向振动下动模量大。在相同圈数下双向振动时土样产生的应变比单向振动时土样产生的应变大,这是由于在双向振动条件下,土样额外受到挤伸作用,而单向振动时只有压应力,所以在双向振动时土样产生的应变大。

2.3 骨干曲线

骨干曲线是受同一固结压力的土在不同动应力作用下每一周期应力—应变关系曲线滞回圈顶点的连线,同时也反映了动应力对动应变的非线性,结果如图8所示。对于骨干曲线,曲线上每一个点的动应力τd和动应变γd均为各自的幅值,其曲线形态接近双曲线,一般比较容易描述。Hardin等[8]提出了目前两种常用的骨干曲线表达方式。

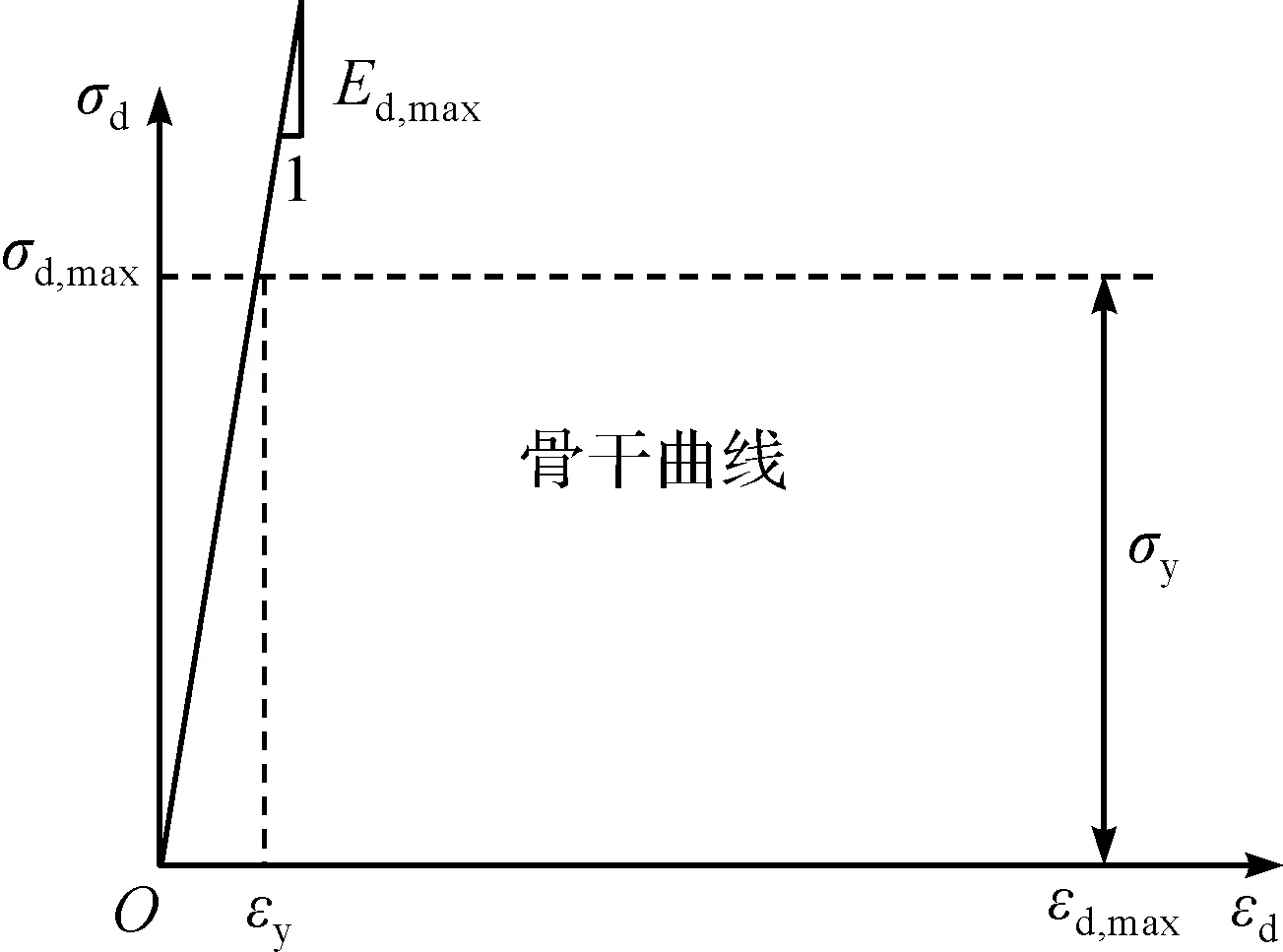
图8 骨干曲线Fig.8 Diagram of backbone curve

通常,采用Hardin-Drnevich的σd-εd曲线(双曲线关系)[8]来分析循环荷载作用下土体的动应力—动应变关系的骨干曲线,即

(1)

故可得动压缩模量函数的基本关系为

(2)

式中:σd,εd分别为动应力幅值和弹性应变;a,b为试验参数。进一步分析上述两式,可得a,b的物理意义,a为最大剪切模量的倒数,b为最大应力幅值的倒数。

图9为单双向振动条件下不同循环圈数下所对应的动应力—动应变关系的骨干曲线,从骨干曲线中可以看到:在不同振动模式下,土体都表现出了应变软化的特点,并且骨干曲线随圈数的增加而右移,初始斜率减小,表明了土样刚度循环衰减的过程。比较图9中单双向振动条件下的骨干曲线可以发现:单向振动条件下的骨干曲线比双向振动条件下的骨干曲线高,且单向振动条件下的初始斜率比双向振动条件下的初始斜率高。说明土样在单向振动条件下的抗剪强度和刚度均比双向振动条件下高,此结论表明振动模式对土样的强度和刚度都有不可忽视的影响。

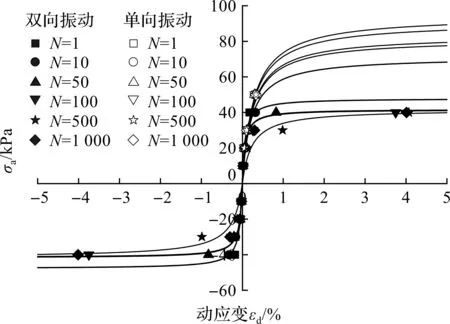
图9 单双向振动条件下不同圈数拟合骨干曲线Fig.9 Backbone curves fitted with test results at different typicalcycle numbers under one-way and two-way cyclic loading

2.4 考虑循环振次的动骨干曲线模型

由图10(a,b)拟合的动应力—动应变骨干曲线参数可建立不同循环圈数下的动骨干曲线模型。图10(a)为双向振动下骨干曲线方程参数b1与循环圈数的关系曲线,图10(b)为单向振动下骨干曲线方程参数b2与循环圈数的关系曲线。拟合参数b1和b2与循环圈数N之间的关系可表示为

b1=n1-n2·ln(N+n3)

(3)

b2=m1-m2·ln(N+m3)

(4)

式中:n1=0.020 64;n2=-0.000 68;n3=0.23;m1=0.002 322;m2=-0.001 236;m3=12.207;N为循环圈数。

图10(a,b)中的曲线为式(1)拟合所得的拟合曲线,该拟合曲线能够较为准确地表达拟合参数b与循环圈数的关系。表3,4中数据是根据式(1,2)与Hardin-Drnevich双曲线模型拟合所得,图10中两种振动模式下骨干曲线的初始斜率接近,a1,a2变化极小,因此直接作为常数。

表3 双向振动条件下拟合参数

表4 单向振动条件下拟合参数

将式(3)代入式(1)中,便可得到不同振动模式下不同循环圈数的动骨干曲线方程,即

(5)

(6)

式中:a1=0.003;n1=0.020 64;n2=-0.000 68;n3=0.23;a2=0.002 3;m1=0.002 322;m2=-0.001 236;m3=12.207。

比较单双向振动条件下的拟合参数b,可发现双向振动条件下的a,b均大于单向振动条件下的a,b,表示同等条件下,单向振动下土体的刚度和强度均比双向振动条件下的刚度大,与前文中的结论一致。

图11(a,b)分别为双向和单向振动状态下实验值与预测值N—εd的关系曲线。比较图11(a,b)中的实验值与预测值可以发现:本研究动骨干曲线模型对实验值的预测较为准确。通过以下公式可以得到预测的N—εd曲线,即

(7)

(8)

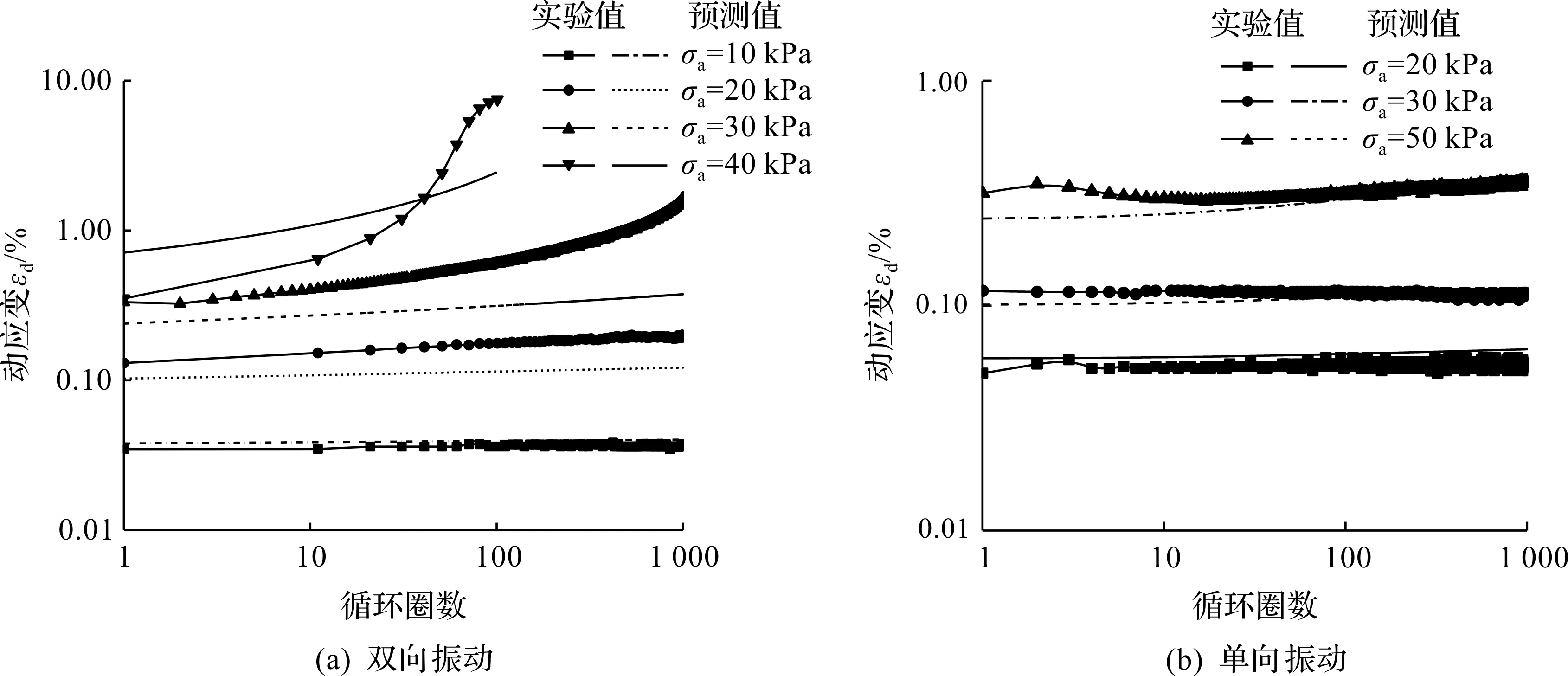
图11 单双向振动状态下实验值与预测值对比Fig.11 Comparison of measured and predicted dynamic strains under one-way and two-way cyclic loading

从以上模型的建立过程可以看出:笔者构建的动骨干曲线考虑了循环圈数的影响,对于循环荷载下易发生软化现象的饱和软黏土来说,该模型更符合实际。考虑到不同振动模式对土体的影响有所不同,笔者分别建立并比较了单双向两种不同振动模式下的骨干曲线模型。

3 结 论

不同的单双向振动模式对循环荷载下饱和软黏土应变发展有显著影响。在相同动应力下,单向振动导致的动应变比双向振动略大,而在相同应力幅值下,单向振动导致的动应变明显比双向振动小。在饱和软黏土的动应力—动应变骨干曲线中,土体初始刚度及动强度随循环圈数的增大均有所减小。同等条件下,单向振动下土体的刚度和强度均比双向振动条件下的刚度大。考虑到不同振动模式对土体的影响有所不同,分别建立并比较了单双向两种不同振动模式下的骨干曲线模型,模型考虑了动应力幅值和循环圈数的影响,所得预测值与实验值较为吻合。