腹板开孔冷弯卷边槽钢双肢拼合梁的整体屈曲性能研究
袁伟斌,孙家贤,赵笙惠,余南霆
(浙江工业大学 土木工程学院,浙江 杭州 310023)
近年来,冷弯型钢拼合受弯构件已被广泛应用于中低层的冷弯型钢结构住宅体系和中等跨度的门式刚架[1]。在实际工程中,为了方便管线布设,冷弯型钢拼合受弯构件多是由2个腹板开孔单肢冷弯型钢构件通过螺钉连接而构成。
周绪红等[2]对双肢拼合冷弯薄壁型钢工字梁进行了试验研究,验证了该拼合截面梁承载力“1×2≥2”的拼合效应,并提出了计算该构件受弯承载力的强度折减修正法。Schafer等[3-4]、Moen等[5]基于大量冷弯型钢构件实验数据,提出了单肢构件的直接强度法(Direct strength method,DSM),该法目前已被北美规范[6]所采用,但直接强度法对于拼合构件的适用性仍需进一步的研究验证。Wang等[7-8]对跨中腹板开孔冷弯薄壁卷边槽钢拼合梁的局部-畸变屈曲性能进行了数值模拟和试验研究,研究发现若单纯叠加单肢构件DSM计算值的结果偏于保守。Ye等[9-10]对实腹冷弯卷边槽钢拼合梁的局部-畸变屈曲进行了试验研究,发现有效截面法和DSM均可较准确计算实腹构件承载力。Chen等[11]在试验的基础上利用有限元分析了孔洞周围的加劲板件对冷弯薄壁卷边槽钢拼合梁承载力的影响,研究发现在孔洞处设置加劲板件能大幅提升构件的承载能力。鉴于目前关于腹板开孔双肢拼合冷弯型钢梁的整体屈曲性能的研究较少,笔者根据经过验证的有限元模型分析螺钉间距、孔洞尺寸、孔洞间距及构件长度的影响,并通过组合效应修正受整体屈曲控制的单肢受弯构件DSM公式。
1 有限元模拟及验证
1.1 有限元模型
采用ANSYS有限元软件的壳单元Shell 181建立半跨构件,本构关系选用理想化的双折线等向强化模型,网格尺寸为10 mm。在模拟构件腹板间的面-面接触时,法向接触关系使用增强拉格朗日算法,切向摩擦系数设为0。采用MPC 184刚性梁单元连接相应结点的方法简化了基本构件连接位置处的自攻螺钉。同时,为了防止加载点处的局部破坏,该单元也被用于耦合加载区域的结点自由度。有限元模型及其简支边界条件如图1所示。

图1 有限元模型Fig.1 Finite element model
有限元分析(Finite element analysis,FEA)过程分为两步:1) 特征值分析,用以获得结构的一阶模态,然后根据一阶模态施加初始几何缺陷值;2) 考虑几何和材料双重非线性的位移控制加载静力分析。
1.2 有限元验证
为验证该有限元模型的准确性,对文献[8]的6组4点弯曲试验构件进行了模拟分析,试件截面尺寸、命名方式、材料参数和初始几何缺陷均取自该文献的数据结果。
冷弯型钢梁有3种主要屈曲模式:1) 构件发生畸变屈曲时,受压翼缘与卷边会绕着腹板-翼缘交线产生转动,板件间交线位置发生改变并不再挺直;2) 在发生局部屈曲时,受压侧腹板或翼缘处产生屈曲变形,板件间交线位置不变且挺直;3) 在发生整体屈曲时,板件间交线不挺直但截面形状不会改变。此外,构件也会发生上述相关屈曲破坏。通过对有限元模型在极限状态时的变形形态来确定构件破坏模式,以OH0.7T1.9-86构件为例,如图2所示,试验和有限元模型均表现出了局部-畸变相关屈曲状态。图3对比了该试件有限元和试验的弯矩—曲率曲线,有限元和实验的曲线在上升段基本吻合,但在接近峰值处于出现分离偏差,主要原因是有限元理想化的本构关系与实际材料存在差异。

图2 有限元屈曲模式与试验屈曲模式对比(OH0.7T1.9-86)Fig.2 Comparison of the deformation between the experimentaland numerical results (OH0.7T1.9-86)

图3 有限元与试验弯矩—曲率曲线对比(OH0.7T1.9-86)Fig.3 Comparison of moment-curvature curves obtainedfrom FEA and test (OH0.7T1.9-86)
表1为各组构件有限元受弯承载力与试验结果对比[8],二者比值的平均值为0.98,标准差为0.03。综上所述,笔者的有限元模型能较好模拟腹板开孔冷弯卷边槽钢双肢拼合梁的4点受弯性能,可在此基础上分析构件整体屈曲性能。
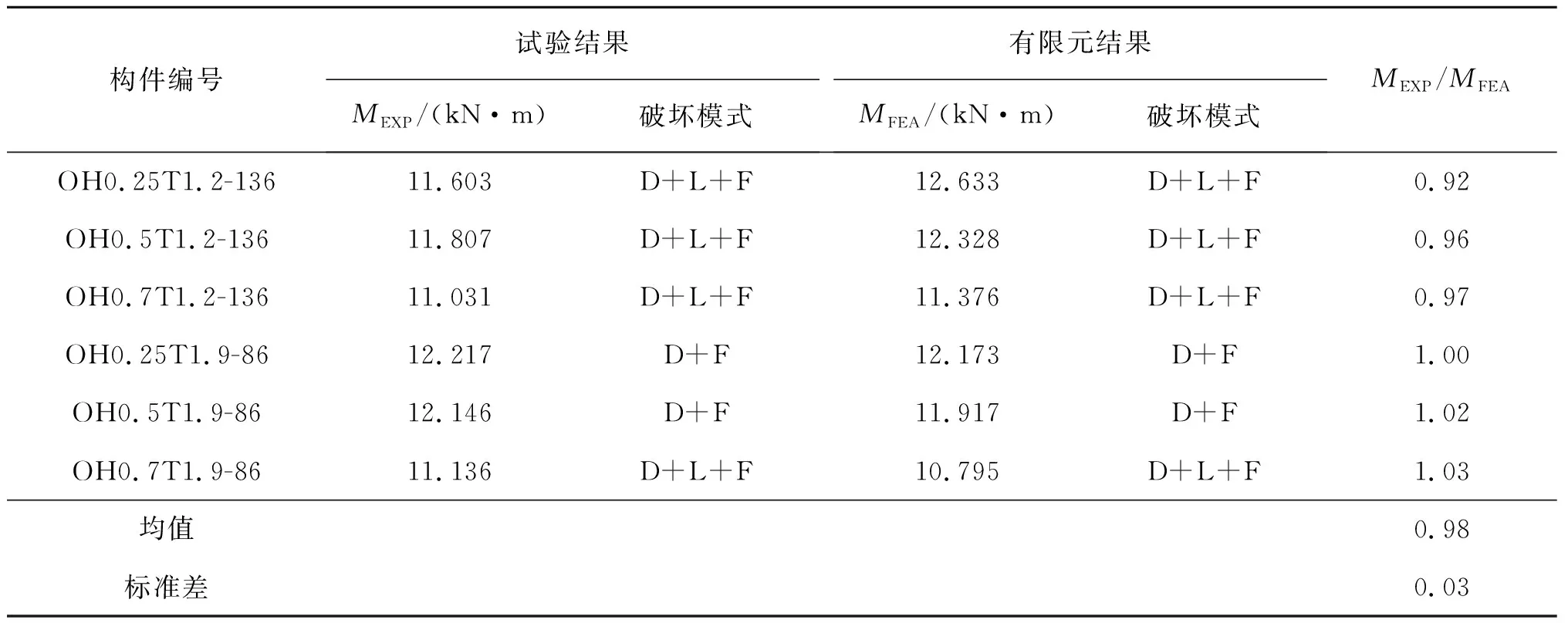
表1 有限元与试验受弯承载力对比
2 参数分析
参数分析时,构件的屈服强度为390 MPa,弹性模量为205 GPa,泊松比为0.3,初始几何缺陷幅值为l/1 000。试件编号规则和构造示意如图4所示,参数分析涉及了H150(hw=150 mm,bf=65 mm,bl=15 mm)和H200(hw=200 mm,bf=75 mm,bl=20 mm)两种截面。图5为构件发生整体屈曲时的变形图。
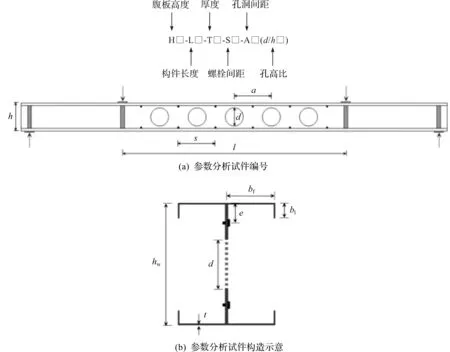
图4 参数分析试件编号及构造示意Fig.4 Specimen labelling rule and structure diagram for the parametric study
2.1 不同螺钉间距的影响
对不同螺钉间距下的H150-L4000-T2.4-A300(d/h=0.5)和H200-L4000-T2.4-A300(d/h=0.5)构件进行了模拟。以H150-L4000-T2.4构件为例,从图6可知:构件承载力随着螺钉间距的减小而增大。相比于无螺钉构件,螺钉间距为50 mm的H150和H200构件的承载力分别增长了9.1%和4.5%。这主要是因为构件受整体弯扭屈曲控制时,螺钉能加强基本构件腹板与腹板间的约束作用。

图6 不同螺钉间距下的腹板开孔拼合梁弯曲承载力对比(H150-L4000-T2.4)Fig.6 Comparison of ultimate moment of CFS built-up beamswith web perforations in different screwarrangements (H150-L4000-T2.4)
2.2 不同孔洞大小的影响
选取腹板孔高比d/h分别为0,0.25,0.5,0.65,0.8,分别对H150-L4000-S150-A300构件和H200-L4000-S150-A300构件进行了参数分析。图7对比了H200构件在不同截面厚度和孔洞大小下的承载力,对于发生整体弯扭屈曲的构件,承载力随着孔洞增大并没有明显降低。随着孔高比d/h从0增大至0.8,H150构件和H200构件承载力分别降低了1.2%和0.8%。这是由于构件在发生整体弯扭屈曲时,其高应力区域首先会出现在一侧单肢构件的上翼缘和另一侧构件的下翼缘;然后逐渐向拼合处延展,构件屈曲时腹板处的应力并不大,因此腹板的孔洞对承载力影响较小。
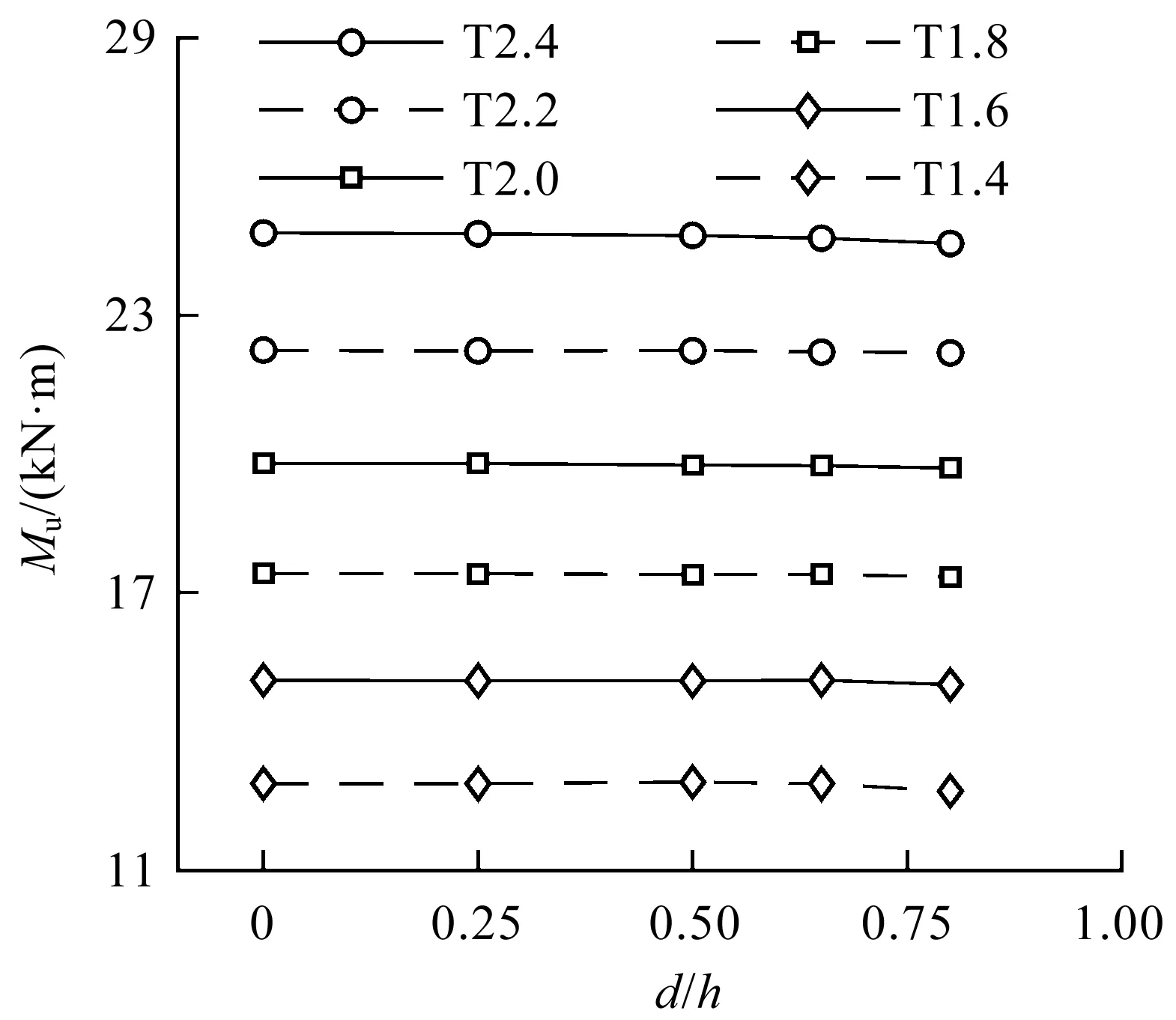
图7 不同孔洞大小下的腹板开孔拼合梁弯曲承载力对比(H200-L4000-S200-A300)Fig.7 Comparison of ultimate moment of CFS built-upbeams with web perforations in differenthole sizes (H200-L4000-S200-A300)
2.3 不同孔洞间距的影响
通过改变孔洞间距大小,对H150-L4000-S150-(d/h=0.5)和H200-L4000-S200-(d/h=0.5)构件进行了分析。H200构件结果如图8所示,受整体弯扭屈曲控制的构件承载力随着孔洞间距增大而增加,但是提升幅度很小,这表明孔洞间距对构件的整体屈曲强度的影响较小。
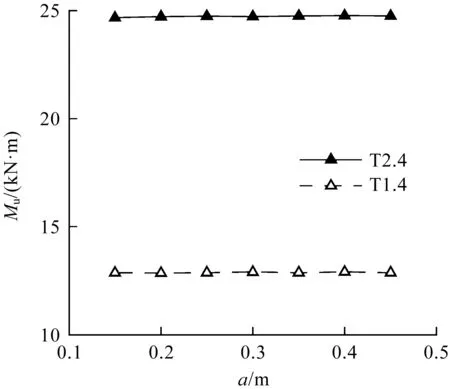
图8 不同孔洞间距下的腹板开孔拼合梁弯曲承载力对比(H200-L4000-S200-(d/h=0.5))Fig.8 Comparison of ultimate moment of CFS built-up beamswith web perforations in different hole spacing(H200-L4000-S200-(d/h=0.5))
2.4 不同构件长细比的影响
以H150-T2.0-S150-A300构件为例,对不同长细比下的构件进行参数分析,构件长度范围为1.2~6.0 m,如图9所示。当长细比较小时(l/i≤30),拼合梁主要发生局部和畸变屈曲;在中等长细比下(30
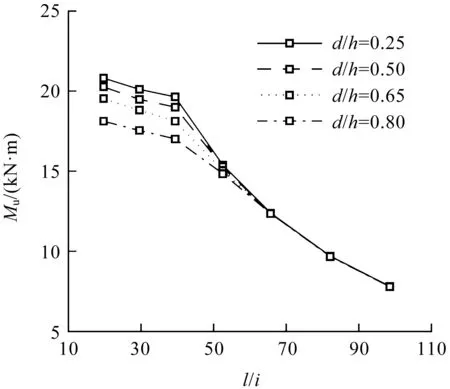
图9 不同长细比下的腹板开孔拼合梁弯曲承载力对比(H150-T2.0-S150-A300)Fig.9 Comparison of ultimate moment of CFS built-up beamswith web perforations in different slendernessratio (H150-T2.0-S150-A300)
3 腹板开孔冷弯卷边槽钢拼合梁直接强度法研究
3.1 冷弯型钢构件DSM公式
北美冷弯型钢设计规范[6]给出了腹板开孔冷弯型钢构件受弯承载力直接强度法计算公式,构件发生整体侧扭屈曲Mne的DSM计算公式为
(1)
式中:My为毛截面边缘屈服弯矩;Mcre为考虑孔洞影响的弹性整体弯扭屈曲临界弯矩。
冷弯型钢构件的弹性临界屈曲弯矩是DSM计算公式的核心环节。由于拼合梁的螺钉以及腹板接触的作用,目前仍很难得到弹性临界屈曲弯矩解析解。因此,将单肢开孔构件DSM计算结果的2倍作为腹板开孔双肢拼合冷弯卷边槽钢受弯构件的DSM计算值。单肢腹板开孔冷弯卷边槽钢梁的弹性整体屈曲临界弯矩Mcre根据文献[12]的计算方法利用Matlab编程计算得到。
3.2 参数分析结果与DSM整体屈曲公式的对比和修正
以构件承载力值Mu与毛截面边缘屈服弯矩My的比值为纵坐标,λe=(My/Mcre)0.5为横坐标,绘制了DSM整体屈曲公式曲线和参数分析数据结果对比图,如图10(图中Mynet为净截面边缘屈服弯矩)所示。DSM公式曲线位于数据点下方且偏离度较大,部分结果值比DSM计算值高出167%。参数分析结果与DSM计算值的比值的平均值为1.66,标准差为0.305,这表明叠加单肢构件的整体屈曲DSM结果的计算方法过于保守。与局部屈曲和畸变屈曲不同,冷弯卷边槽钢拼合梁发生整体屈曲时,构件间不会独立屈曲,而是作为整体发生屈曲。因此,在叠加单肢构件承载力作为拼合梁的承载力值时,需要考虑组合效应的影响。

图10 以整体侧扭屈曲为主的开孔拼合构件DSM原始曲线及有限元结果对比Fig.10 Comparison of the origin DSM curves and FEA resultsfor CFS built-up beams with web perforationscontrolled by global lateral-torsional buckling
根据参数分析结论可知:构件的长细比及螺钉间距对其整体屈曲承载力有着明显的影响。为考虑长细比对组合效应的影响,以长细比l/i为横坐标,构件承载力值Mu与原始DSM整体屈曲计算值Mne,o的比值为纵坐标,将螺钉间距等于腹板高度(s/h=1)的整体屈曲数据结果按Mynet/My归类作图,如图11所示。随着长细比的增大,组合效应值越来越大,且在相同长细比下,Mynet/My越小组合效应值越大。同时,为考虑螺钉作用对组合效应的影响,以螺钉间距和腹板高度的比值s/h为横坐标,构件承载力值Mu与Mu-s/h=1的比值为纵坐标,如图12所示。
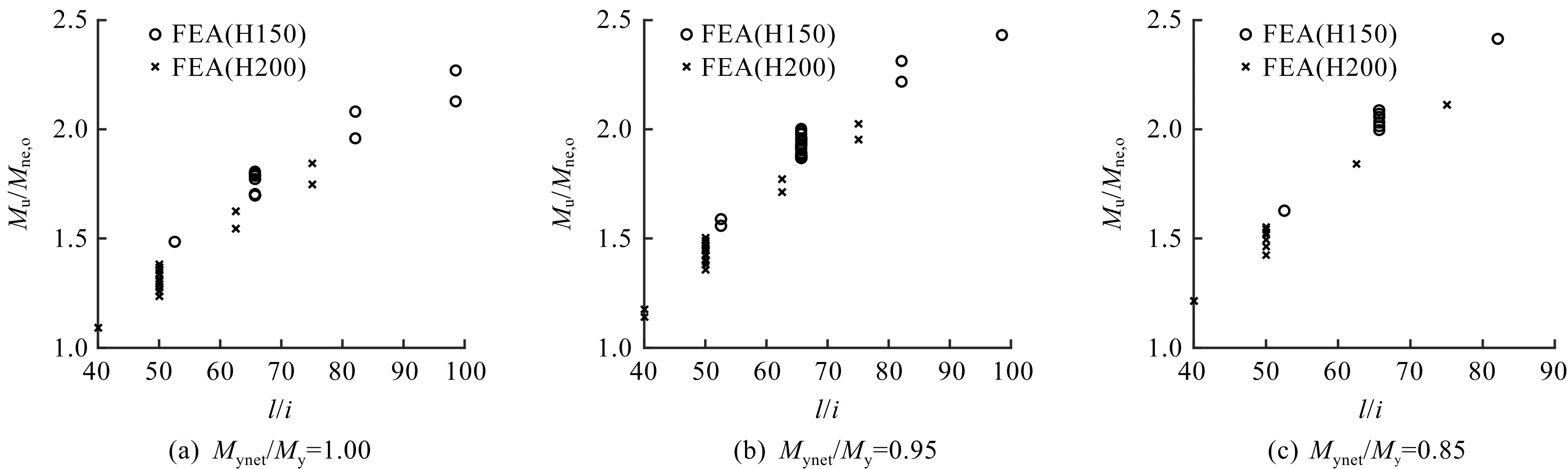
图11 不同长细比下以整体侧扭屈曲为主的开孔拼合构件有限元结果与原始DSM计算值对比Fig.11 Comparison of FEA results and design strength calculated by original DSM for CFS built-up beams with webperforations failed by global lateral-torsional buckling in different slenderness ratio
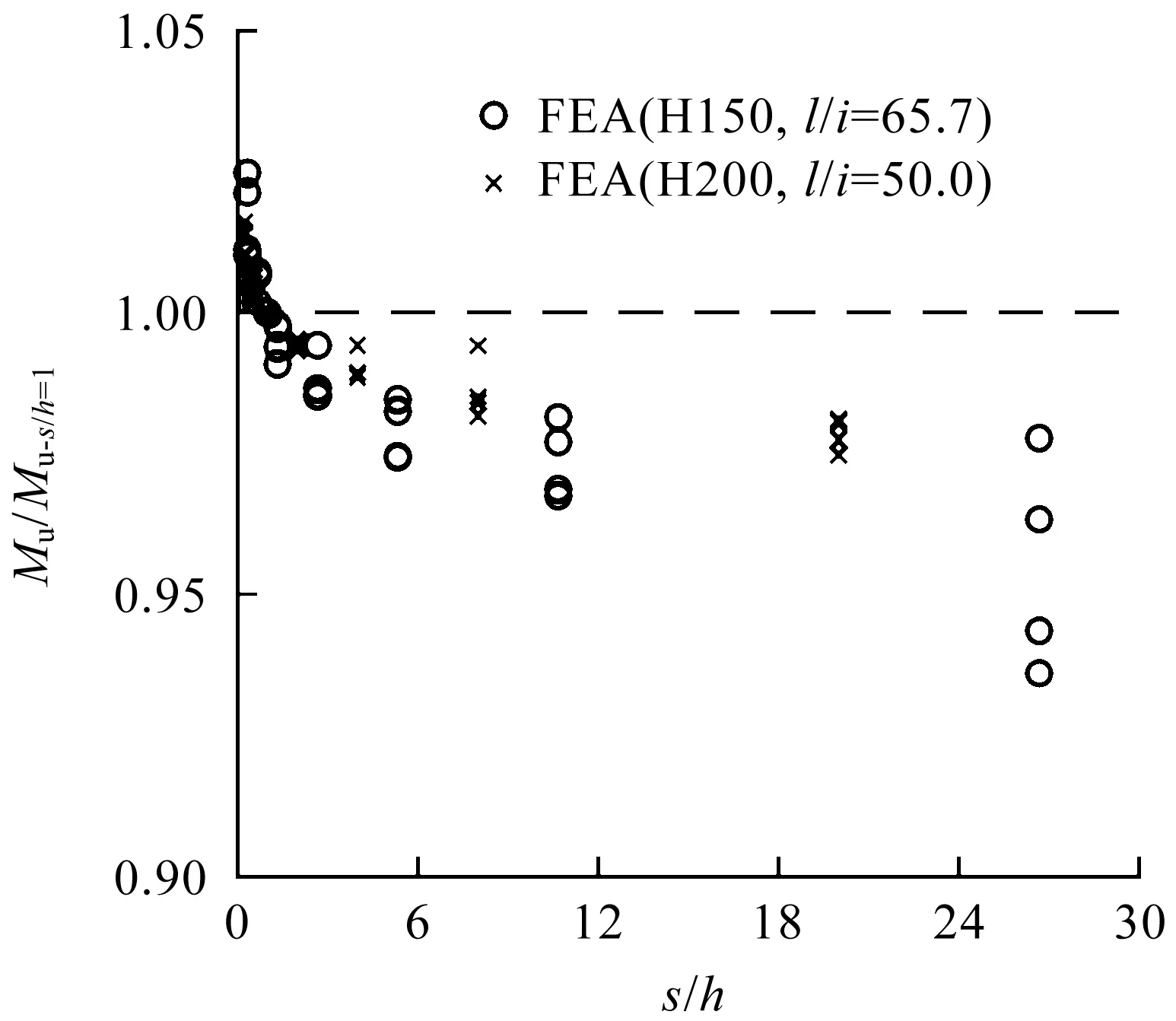
图12 不同螺钉间距下以整体侧扭屈曲为主的开孔拼合构件有限元结果对比Fig.12 Comparison of FEA results for CFS built-up beamswith web perforations failed by global lateral-torsional buckling in different screw spacing
为了量化长细比和螺钉间距的影响,分别对图11,12数据散点进行拟合,引入了长细比修正因子γe和螺钉间距修正因子ψe,修正后的计算式为
Mne,m=ψeγeMne,o=2ψeγeMne
(2)
γe=(-5.026η2+6.595η-0.282)ln(l/i)+
9.449η-13.15
(3)
(4)
式中:η=Mynet/My;s为螺钉间距;h为构件腹板高度;l/i为构件长细比;Mne为单肢开孔构件的整体屈曲DSM计算值,通过式(1)计算。
图13对比了修正式和有限元结果,修正式与参数分析结果比值的平均值为1.00,标准差为0.04。
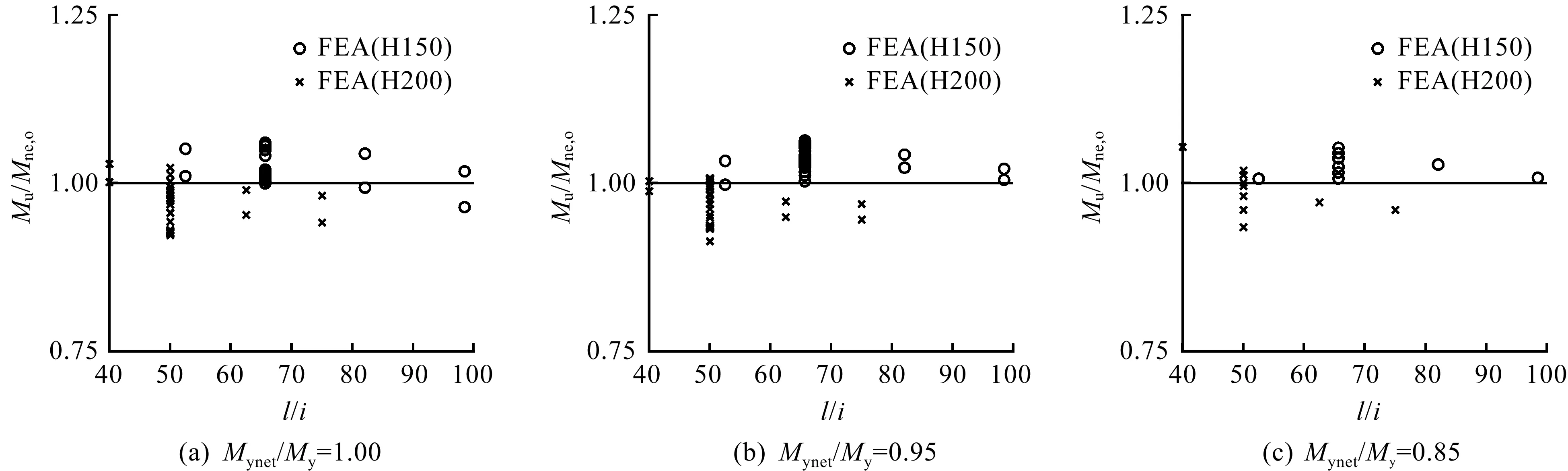
图13 不同长细比下以整体侧扭屈曲为主的开孔拼合构件有限元结果与修正DSM计算值对比Fig.13 Comparison of FEA results and design strength calculated by modified DSM for CFS built-up beams with webperforations failed by global lateral-torsional buckling in different slenderness ratio
4 结 论
利用经过验证的有限元模型分别在螺钉间距、孔洞大小、孔洞间距和长细比4种因素下对腹板开孔冷弯卷边槽钢双肢拼合梁进行了分析。结果表明:随着螺钉间距的增大,构件整体屈曲承载力逐渐降低;对于孔洞间距为300 mm的构件,不同孔洞大小对整体屈曲承载力影响较小;当构件孔高比小于0.5时,孔洞间距对整体屈曲荷载影响也很小;随着长细比的增长,构件的承载力逐渐降低,构件也从局部和畸变屈曲逐渐转为整体屈曲。另外,考量了长细比和螺钉间距对构件组合效应的影响,修正了受整体屈曲控制的单肢构件的DSM公式,修正后的公式能较准确计算拼合构件的整体屈曲承载力。

