钢结构聚氨酯涂层力学性能及抗冲击性能的有限元分析

霍俊芳,李海青,郝贠洪,3,宣姣羽,慈天义,查克乐汗

(1.内蒙古工业大学土木工程学院,呼和浩特 010051;2. 内蒙古工业大学内蒙古自治区土木工程结构与力学重点实验室,呼和浩特 010051;3.内蒙古自治区建筑检测鉴定与安全评估工程技术研究中心,呼和浩特 010051)

表面涂层能极大改善钢结构的表面性能,从而对钢结构起到保护作用。内蒙古中西部地区是我国沙尘暴爆发较频繁的地区之一[1]。该地区的钢结构设施如钢结构厂房、桥梁、大跨结构、塔桅结构等由于长期受到风沙等硬质颗粒的冲击而损伤。有机涂层如聚氨酯涂层,因具有良好的耐蚀性以及柔韧性等特点,在钢结构防护方面得到了广泛应用,但由于其在固化过程中产生较多微孔隙,硬度和屈服强度较低,对风沙的抗冲性能较差。因此,研究分析钢结构聚氨酯涂层力学性能及抗冲击性能,对钢结构涂层在西部地区的工程应用具有重要的意义。

目前,研究者们通过理论、试验及数值模拟等方法对金属材料和脆性硬质涂层受固体颗粒冲蚀进行了研究,且取得了不少进展,研究内容主要包括固体颗粒在冲击涂层过程中的应力、应变响应规律,冲击磨损行为和特征及塑性应变响应[2-6]。现有研究多集中于较小固体颗粒冲蚀条件下[7-8],且主要分析了冲击速度和角度对涂层冲蚀损伤机理和剥落行为的影响[9-12],而针对弹塑性材料涂层的研究较少。本工作采用有限元分析软件ABAQUS建立了二维平面对称模型,模拟得到聚氨酯涂层应力-应变曲线;并基于该应力-应变关系,建立具有不同厚度聚氨酯涂层的钢结构的三维冲击模型,通过与文献[13]的试验结果对比验证模型的准确性,并研究不同涂层厚度下钢结构聚氨酯涂层的抗冲击性能。

1 聚氨酯涂层应力-应变曲线的模拟计算

1.1 几何模型的建立

由于ABAQUS有限元分析软件的二维与三维模型都能满足模拟精度[14-15],为了减少有限元计算规模,建立微米压痕试验过程的二维平面模型。该模型的结构、施加载荷及约束条件均为对称,故仅取模型的一半进行模拟分析。

压头设置为半锥角70.23°的圆锥压头[16-17],由于压头材料硬度远大于被测材料,在有限元模拟过程中将其设置为线性解析刚体,以大幅减少计算量。假设聚氨酯涂层和钢板之间结合良好,即界面处没有分层或滑移,并假设压头与涂层表面不存在摩擦力[18]。通过试算确定冲击变形的影响范围,并参考微米压痕试验[19]实际试件尺寸,将覆有聚氨酯涂层的钢结构设置为半径5.8 mm,厚度5.8 mm的圆柱体,聚氨酯涂层的厚度为0.8 mm。基体与涂层均采用轴对称四边形减缩积分单元(CAX4R),在压头附近、中心轴线处网格划分较密,而在远离中心的外侧边界处网格划分较稀疏,如图1所示。圆锥压头与聚氨酯涂层的接触设置为面面接触。有限元模拟过程中,设置了加载和卸载两个分析步。加载速度对分析过程的影响很大,速度越慢,模拟结果与实际结果越接近,但所需的计算时间就越长。分析步时间的选择不仅要保证模拟结果的可靠性,还要保证在可接受的时间内完成计算,其时间选择如图2所示。

图1 钢结构聚氨酯涂层平面对称模型及网格划分Fig.1 Plane symmetry model and mesh division of steel structure polyurethane coating

图2 载荷-时间曲线Fig.2 load-time curve

1.2 材料参数

聚氨酯涂层、钢基体和冲击模型中冲击球体的材料参数[19]如表1所示。

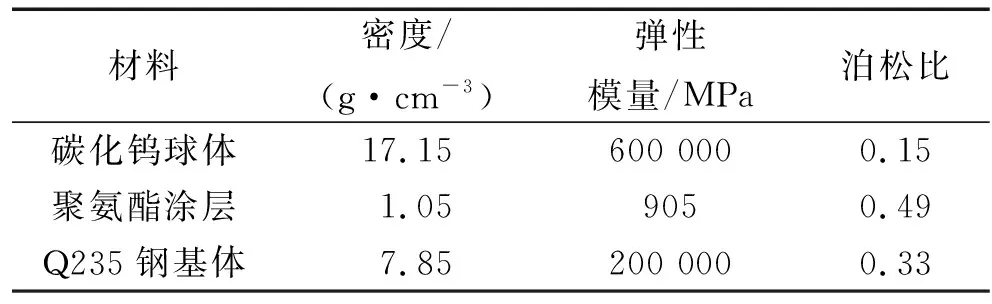
表1 模型中的材料参数Tab.1 Material parameters in the model

1.3 聚氨酯涂层塑性特性分析

通过有限元软件可进行正向分析,即设定材料的不同力学性能参数(屈服强度、弹性模量、密度和表示塑性性能的应力应变),模拟微米压痕试验的加载-卸载过程。运用有限元软件也可对模拟微米压痕试验进行反演分析,得到测材料的塑性性能参数,推导出材料的应力-应变关系[20]。微米压痕试验过程为准静态过程,压头慢慢压入,压头与涂层之间的摩擦可忽略。假设聚氨酯材料为均匀、各向同性材料,且涂层与钢基体定义为完全结合。有限元模拟初始阶段,选用特性相近的已知材料的应力-应变曲线进行有限元计算[21],以试验所得的荷载-位移曲线为基准进行比较。如果初选材料的性能参数是正确的,那么有限元模拟计算得到的荷载-位移曲线应该与微米压痕试验所得的曲线相符合;否则,需要不断调整聚氨酯涂层应力和应变值,每次改动量不能太大,如此反复,直到有限元模拟得到的荷载-位移曲线与微米压痕试验得到的荷载-位移曲线相吻合为止,最终确定聚氨酯涂层材料实际的应力-应变曲线。经过调整聚氨酯涂层材料的应力、应变值后,得到的荷载-位移曲线如图3所示。有限元计算结果与试验结果[19]总体变化趋势基本一致,最大位移时荷载为0.255 N,与试验结果的相对误差为4.16%,模拟得到的曲线与试验得到的曲线很好吻合,说明该有限元模型能够真实地反映聚氨酯涂层应力-应变的变化和钢结构聚氨酯涂层的微米压痕试验过程,验证了该模型的准确性。最终确定聚氨酯涂层的应力-应变曲线如图4所示。应力-应变曲线中第一个点处的应力为多线性材料的屈服应力,因而可以确定聚氨酯涂层的屈服强度为1.86 MPa。

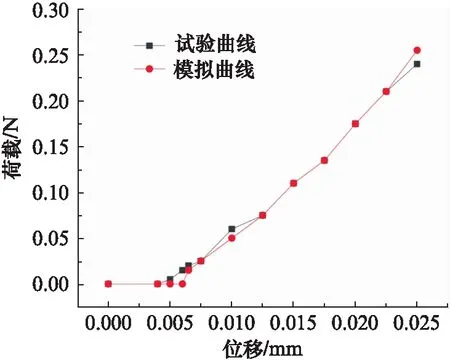
图3 聚氨酯涂层的荷载-位移曲线Fig.3 Load vs displacement curve of polyurethane coating

图4 聚氨酯涂层的应力-应变曲线Fig.4 Stress vs strain curve of polyurethane coating

2 三维冲击模型

2.1 几何模型的建立

使用ABAQUS有限元分析软件建立球体冲击钢结构聚氨酯涂层三维有限元模型,涂层厚度分别为0,0.2,0.4,0.6,0.8,1.0,1.2 mm。模拟研究的对象主要为涂层及基体材料,且冲击球体材料硬度远大于被测材料,因此不考虑球体的破坏形式,有限元模拟分析中,在满足模拟精度前提下,为了提高计算效率,球体采用刚性球体,球体直径为10 mm,球体模型采用1/4模型,基体的长、宽、高分别为50,50,5 mm。图5所示为球体冲击钢结构聚氨酯涂层的有限元模型和网格划分。小球网格采用三维四面体单元C3D4划分,涂层-基体网格采用三维六面体减缩积分单元C3D8R来划分。为提高模拟精度,对冲击中心区域的网格进行了致密化处理。冲击过程中球体与涂层接触采用面面接触,假设聚氨酯涂层和钢板之间完全结合,通过在两种材料的界面处合并节点,实现基体与涂层结合。有限元模型中沿涂层-基体方向的平面设置对称约束,为了避免应力波的影响,对基体底面和其他侧面设置固定约束,球形压头沿冲击方向的初始速度为5 m/s,冲击角度为90°,冲击总时间为0.5 ms。

图5 球体冲击钢结构聚氨酯涂层的有限元模型和网格划分Fig.5 Finite element model and meshing for sphere impacting polyurethane coating of steel structure

2.2 钢板本构模型的建立

基体Q235钢和聚氨酯涂层均为弹塑性材料。针对基体Q235钢材料,选用Cowper-Symonds本构模型[22],如式(1)所示,进一步研究球体冲击作用下基体的动态响应。

(1)

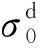
2.3 冲击损伤评价指标

球体冲击过程中的能量转化可分为两个阶段。首先,球体的初始动能转化为靶材的内能(弹性变形能、塑性耗散能与摩擦引起的能量三者之和);其次,在球体回弹阶段，靶材弹性变形恢复,返还给球体一部分动能。若为纯弹性接触,则压头在撞击过程中没有能量损失,入射动能等于回弹动能。若为弹塑性接触,则在撞击后只有部分动能返还,另外一部分动能转化为摩擦引起的内能和靶材的塑性变形能。假设球体为刚体,并且不考虑摩擦力的影响(摩擦因数为0),即假设摩擦引起的内能为0,则球体损失的动能全部转化为靶材的塑性变形能,如式(2)所示。

▽E=Ep

(2)

K为能量转化系数[23]:

(3)

式中:E1为冲击前球体动能,E2为冲击后球体动能,ETotal为系统总能量,单位均为mJ。K值越大,表示靶材吸收冲击能量的能力越强;K值越小,表示靶材吸收冲击能量的能力越弱。

2.4 冲击模拟可靠性分析

通过ABAQUS有限元软件建立球体冲击钢板模型,根据文献[13]球体冲击钢板响应过程模拟,设置球体冲击速度为1 m/s,球体为直径20 mm的钢球,得到冲击力时间历程,并与文献[13]给出的数值解进行对比。由图6可见,误差的影响较小,说明该有限元冲击模型是可行的。

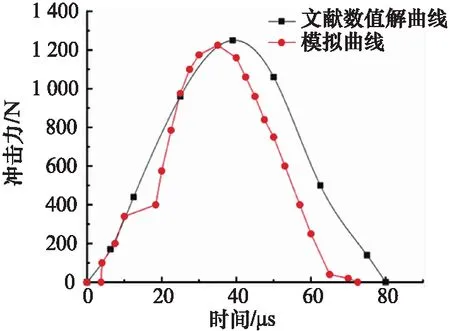
图6 球体冲击钢板模型模拟的冲击力时间历程Fig.6 Time history of impact force simulated by sphere impacting steel plate model

3 结果与讨论

3.1 能量守恒

由于本研究中没有考虑摩擦力的影响,并假设冲击球体为刚性,因此系统能量仅在球体的动能和靶材的内能(无摩擦引起的内能)之间转化。系统能量随时间的变化如图7所示,能量从动能(ALLKE)转化到内能(ALLIE),而内能由弹性变形能(ALLSE)和塑性耗散能(ALLPD)组成。

由图7可以看出:在0.43×10-4s时,系统动能为0,而弹性变形能上升到峰值,塑性耗散能随着钢结构涂层的永久变形不断上升;0.43×10-4s后,动能出现反弹上升,弹性变形能降低,塑性耗散能上升;0.5×10-4s后,系统能量稳定;将球形压头冲击过程中任一时刻的动能和内能相加,即得到系统总能量(ETOTAL),在整个碰撞过程中,系统总能量保持一恒定值,即系统能量守恒。

图7 球体冲击过程中的能量转化Fig.7 Energy conservation during sphere impact

3.2 涂层厚度对能量及其转化系数的影响

聚氨酯涂层厚度对系统动能的影响如图8所示,图中显示球体冲击后无涂层钢板的动能为2.75 mJ。涂层厚度为0.2 mm时,冲击后的动能为1.6 mJ。随着涂层厚度的增加,动能在入射阶段的衰减速度降低,即冲击缓冲时间增加,且随着涂层厚度的增加,冲击缓冲时间增加的幅度减小;在弹性恢复阶段所返还的动能增加,即随着涂层厚度的增加,其吸收能量的能力减弱。当涂层厚度为0.8 mm时,冲击后返还的动能为4.2 mJ,然后随着涂层厚度增加返还动能趋于稳定。

图8 聚氨酯涂层厚度对系统动能的影响Fig.8 Effect of polyurethane coating thickness on kinetic energy of system

聚氨酯涂层厚度对能量转化系数的影响如图9所示。从图9可以看出:随聚氨酯涂层厚度的增加，能量转化系数先增加后减小,当涂层厚度为0.2 mm 时,能量转化系数达到最大值,为0.943;当涂层厚度大于0.8 mm后,能量转化系数稳定在0.85左右。以上结果表明,钢结构聚氨酯涂层吸收冲击能量的能力随着涂层厚度的增加先增加后减小,当涂层厚度为0.2 mm时,吸收冲击能量的能力最强。由于涂层和基体在材料性能、结构方面存在差异,导致两者能量转化系数不同。涂层厚度较薄时,冲击球体与靶材的接触面积小,导致界面间的接触应力较高,试样更易发生塑性变形和材料去除,因此涂层厚度为0.2 mm时,靶材表现出较高的吸收冲击能量的能力。随着涂层厚度的增大,球体接触面积增大,接触应力降低,能量转化系数降低。当涂层厚度超过0.8 mm后,能量转化系数达到一个动平衡的状态。

图9 能量转化系数随聚氨酯涂层厚度的变化Fig.9 Relationship between energy conversion coefficient and polyurethane coating thickness

3.3 涂层厚度对接触冲击力的影响

聚氨酯涂层厚度对冲击力时间历程如图10所示。冲击模型采用1/4模型,实际冲击力为该图中冲击力的4倍。从图10中可见,无涂层(涂层厚度为0)钢板受到冲击时间较短,且受力峰值较大,随着涂层厚度的增大,聚氨酯涂层钢板受到的冲击时间延长,这可以延缓冲击过程,减小冲击力,说明在受到冲击的情况下,聚氨酯涂层可以争取更多的时间,从而减小冲击带来的破坏。涂层厚度的增大使冲击→静止(动能耗尽)、静止→反弹(弹性应变能释放)这两次运动状态的改变耗时更长,进而导致整个接触所需的时间更多,接触冲击力减小。

图10 聚氨酯涂层厚度对冲击力时间历程的影响Fig.10 Effect of polyurethane coating thickness on time history of impact force

最大接触冲击力随聚氨酯涂层厚度的变化如图11所示。冲击模型同样采用1/4模型,因此实际最大冲击力为该图中最大冲击力的4倍。由图11可见:随着涂层厚度不断增大,钢板表面最大接触冲击力减小,单位厚度增长对应的冲击力变化幅值不断减小。这表明聚氨酯涂层对球体冲击有减缓作用,涂层的减缓能力随其厚度增大而增大,但增长幅度逐渐减小,这与涂层厚度对材料动能影响分析得到的结论是一致的。根据涂层厚度对材料动能及表面冲击力的分析可知,表面涂覆聚氨酯涂层有助于材料减少因球体冲击产生的损伤,故需根据数值模拟及试验结果进一步分析涂层合理厚度,使其兼顾耐久性与经济性。

图11 最大接触冲击力随聚氨酯涂层厚度的变化Fig.11 Relationship between maximum contact impact force and polyurethane coating thickness

3.4 残余应力沿深度方向的分布

冲击中心点处残余应力沿深度方向的分布如图12所示。由图12中可以看出,无涂层钢板和涂层厚度0.2 mm的钢板受冲击后残余应力相对较大,涂层厚度0.4 mm的钢板受冲击后残余应力相对最小,聚氨酯涂层厚度超过0.4 mm后,残余应力相对较小。这说明同样冲击条件下,聚氨酯涂层具有减小冲击后靶材残余应力的作用。

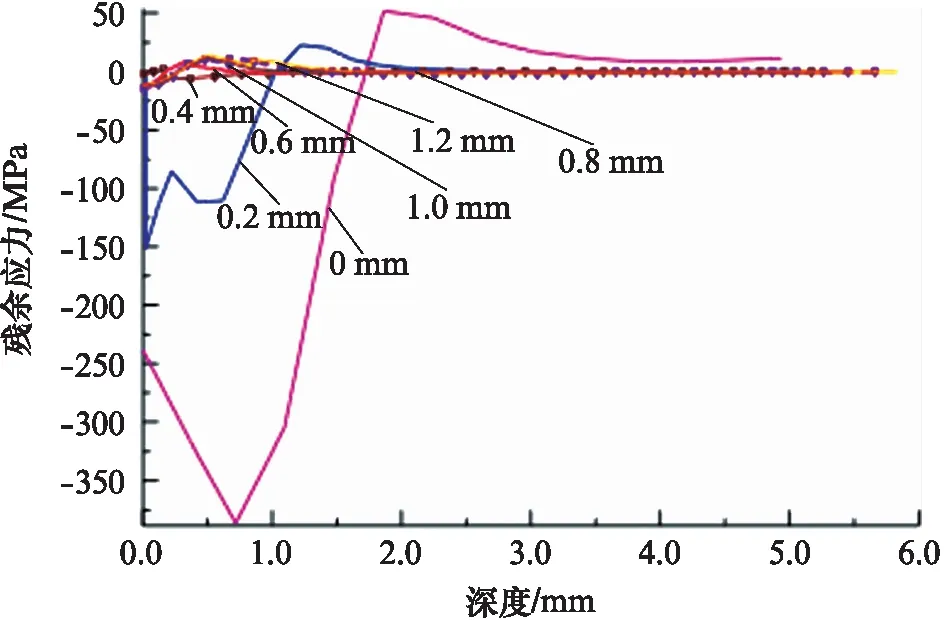
图12 冲击中心点处残余应力沿深度方向的分布Fig.12 Residual stress distribution along depth at impact centre

3.5 涂层最优厚度

材料的动力学响应差异反映了其抗冲击性的优劣,响应包括冲击力波形特性(最大冲击力,持续时间)和冲击动能的能量耗散[24]。通过前面的分析可知,当参数条件一定时,聚氨酯涂层厚度的增加对能量耗散、接触冲击力时间历程及冲击后靶材残余应力都有影响。当涂层厚度为0.8 mm时,能量吸收系数趋于稳定,涂层的减缓能力随其厚度增大而增大,但增长幅度逐渐减小,考虑到加大聚氨酯涂层厚度会降低叶片的附着力,且成本提高,因此,钢结构表面聚氨酯涂层较为适宜的厚度为0.8 mm。

4 结论

(1) 利用ABAQUS有限元分析软件建立微米压痕试验的二维平面模型,模拟得到聚氨酯涂层材料的应力-应变曲线,确定其屈服强度为1.86 MPa。

(2) 当球体半径及速度一定时,能量转化系数随聚氨酯涂层厚度的增大先增加后减小,涂层厚度0.2 mm时,能量转化系数达到最大值,为0.943,即吸收冲击能量的能力最强。

(3) 涂覆涂层钢板和无涂层钢板对比分析可知,同样冲击条件下,聚氨酯涂层具有减小冲击力的作用。随着聚氨酯涂层厚度增大，涂层对冲击力的减缓作用增大。

(4) 无涂层钢板和涂层厚度0.2 mm钢板的残余应力较大,聚氨酯涂层厚度超过0.4 mm后,冲击后残余应力相对较小。区域环境中,钢结构聚氨酯涂层的适宜厚度为0.8 mm。