串联式振荡水翼的纵向间距对获能的影响

何广华， 莫惟杰， 王 威， 杨 豪

(1. 哈尔滨工业大学 机电工程学院，哈尔滨 150001； 2. 哈尔滨工业大学(威海) 海洋工程学院，山东 威海 264209； 3. 山东船舶技术研究院 船舶与海洋工程水动力研究所，山东 威海 264209)

我国对于清洁的可再生能源发展需求日益增大，国家大力支持可再生能源研究建设，保护生态环境，推进清洁生产、推动绿色低碳可持续发展。振荡翼水流能发电装置可以从河流和海洋流中提取能量，该技术相比于传统的风能和太阳能发电，具有更大的能量密度[1]和可预测性[2]。同时，相比于相对成熟的水平轴旋翼发电装置，振荡水翼具备：启动流度低、运行速度慢和发电效率高三大优势。

来源于鸟类翅膀上下振荡摆动获得升力的启发，振荡翼获能研究最早始于1981年，Mckinney等[3]的振荡翼试验研究发现，当水翼升沉和俯仰运动的相位差在π/2附近时，获能效率最大，指出了其优异的获能能力。近些年清洁新能源开发研究受到重视，振荡翼水流能发电装置的新奇设计也受到研究人员的广泛关注。目前，振荡翼获能研究主要分为3种类型，全主动式、半主动式和全被动式[4]；全主动式就是强制水翼按照给定规律同时做升沉和俯仰运动，研究该运动模式下水翼的获能机理。

全主动式因其规律可控，取得的研究成果非常丰富。Liu[5]提出了根据有效攻角公式来衡量振荡翼获能的方式，并据此提出了一种以最大有效攻角为特定参数来区分水翼的推进和获能两种模式的方法。随着人们研究的深入，发现振荡翼表面的涡脱落会对获能产生积极作用；Simpson[6]在雷诺数Re为13 800的条件下对振荡翼的获能情况进行了试验研究，得到最大获能效率为45%，同时对振荡水翼的流场做了分析，总结了运动频率和振幅对流场中涡分布的影响规律，并对不同涡分布形式下的获能情况进行了分类。Kinsey等[7]在雷诺数为1 100时对振荡翼的获能情况进行了数值研究，发现获能的最优区域在折算频率f*=0.12～0.18，俯仰角θ0=70°～80°，最大获能效率可达34%，并发现明显的涡脱落现象。在此基础上又对Re=500 000时进行了参数化分析[8]，发现随着水翼升沉振幅的增加，最优的获能区域逐渐向低运动频率、高俯仰振幅移动。Deng等[9]在研究中发现，前缘涡脱落现象发生后，涡将会沿着翼身向后缘移动，使升力与升沉速度获得更佳的同步性。动网格技术为实现水翼全主动式控制提供了必要技术条件，王威等[10]运用动网格技术让双翼在上游周期性摆动，形成了周期性来流的条件。何科杉等[11]分析了尾缘襟翼对荷载频率的敏感程度。刘龙等[12]采用URANS(unsteady Reynolds averaged Navier-Stokes)方法分析了具有两个自由度三维刚性水翼的振动和噪声问题，其中重点计算了质量静矩和质量惯性矩对水翼振动的影响。李国俊等[13]研究发现了翼在失速时前缘漩涡的产生和尾涡脱离是一种能量转换和输入机制。

对于串联排列水翼，Kinsey等[14-16]进行了串联样机的试验和数值研究，总获能效率最高可达40%左右，并提出用总体相位来评价串联水翼的获能效率，在总体相位大约为π/2时总获能效率最高，且上游翼产生的涡脱落在特定的全局相位下对下游翼的获能将起到促进作用。Ma等[17]研究了半主动式串联水翼的获能情况，发现在上游水翼的尾迹流场中，下游水翼的获能效率会比较差，所以应该尽量避免下游水翼受到上游尾迹的影响。Xu等[18]采用速度势流理论对串联水翼的获能进行了分析，找到了最优的总体相位和尾涡模式。Pourmahdavi等[19]研究了水深对串联水翼的获能影响，发现相较于深水情况，水翼在浅水域中的获能效率会降低。Xu等[20]研究发现振荡翼在运动过程中前缘涡的形成和脱离会对装置的获能产生很大的影响，在最优的情况下，双水翼获能装置的效率可以达到53.8%。 Srinidhi等[21]研究了当雷诺数Re=100时串联双翼在地面效应作用下的获能情况，研究发现后翼的升力变化受到前翼尾涡在地面约束下的影响。在没有相位差时，两翼的升力最大，在相位差为π时两翼的稳定性最佳。Yang等[22]发现双水翼串联在地面效应作用下，后翼的升力会有所提升，但是获能会降低。Dahmani等[23]发现在改变串联翼的布置情况时，两翼的总获能可以提升23%。Karbasian等[24]研究了低雷诺数下串联水翼的获能情况，发现在较低运动频率时的获能较高，在多级串联情况下，第二级水翼后获能会明显减少。

已发表的文献研究基本都是考虑前后串联双翼平衡位置齐平的一般情况，提升获能效果有限。对于高雷诺数下串联水翼错位排列这种特殊情况的研究还非常少，为了能够有效提高下游翼的获能，使整个系统取得更高的获能功率，本文进一步分析了串联式振荡水翼的纵向错位排列对获能的影响，并深入分析获能提升的原因，总结了上游水翼尾涡对下游水翼流场的影响规律。

1 数学模拟方法及验证

1.1 数学模型

文中数学模型涉及的控制方程如下

连续性方程

(1)

式中：ρ为流体密度；t为时间；ui为流体介质在笛卡尔坐标轴i方向上的速度分量；xi为i轴方向的坐标，i=1，2，3。

动量方程

(2)

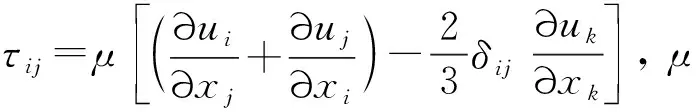
1.2 水翼运动的参数方程

给定水翼的运动轨迹为

h(t)=h0cos(2πft)

(3)

θ(t)=θ0sin(2πft)

(4)

式中：h为水翼的垂向位移；h0为升沉振幅；f为水翼的振荡频率；θ为水翼绕转轴的俯仰角；θ0为俯仰角的幅值。

1.3 水翼的获能效率

水翼的阻力系数CD、升力系数CL、力矩系数CM分别为

(5)

(6)

(7)

式中：FD，FL，M分别为水翼所受的阻力、升力和力矩；U∞为来流速度；S为水翼的弦长c与展长b的乘积，文中b取值为单位长度。

水翼获能的瞬时功率P为升力FL与俯仰力矩M做功之和，即

(8)

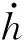
(9)

式中，T为水翼的振荡周期。

水翼的瞬时功率系数CP为

(10)

(11)

振荡水翼的总功率P0定义为

(12)

式中，d为水翼的竖向扫掠高度，它与展长b的乘积为水翼的扫掠面积。

振荡水翼在水流中的获能效率η为

(13)

1.4 模型设置及验证

1.4.1 模型设置

本文采用开源计算流体软件OpenFOAM开展数值研究，水翼弦长c=0.25 m，来流速度为2 m/s，雷诺数Re=500 000；采用Spalart-Allmaras单方程湍流模型进行计算。水翼振荡采用任意欧拉拉格朗日法在动网格上求解，控制方程为

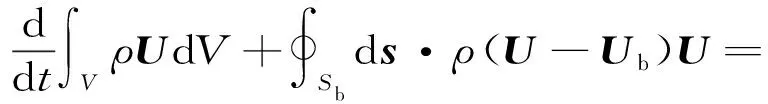
(14)

式中：U为流体速度；Ub为有限控制体边界速度；Sb为有限控制体边界。

时间项采用欧拉隐式离散，压力速度耦合采用Pimple算法。计算域网格，如图1所示。水翼周围及流场核心区域的网格加密处理，以保证上游水翼产生的尾涡在向下游传递过程中耗散减少。计算域大小为60c×60c；上游左侧边界为速度入口，下游右侧边界出口为压力出口，上下双侧边界均为滑移壁面条件。网格主要分为左、右两个区域，中间采用滑移边界，每个区域内分为弹性变形区和非变形区，水翼上下升沉运动时，在弹性变形区内(虚线框中的上下两处区域)网格产生拉伸变形，其余中间区域非变形网格为刚体运动(包括与虚线相交的网格)；水翼的俯仰运动通过中间圆形网格区域的转动实现，圆形滑移边界在不影响流体运动规律的同时保证内部网格绕水翼中心转动。水翼的前缘和后缘网格细节，见图1。

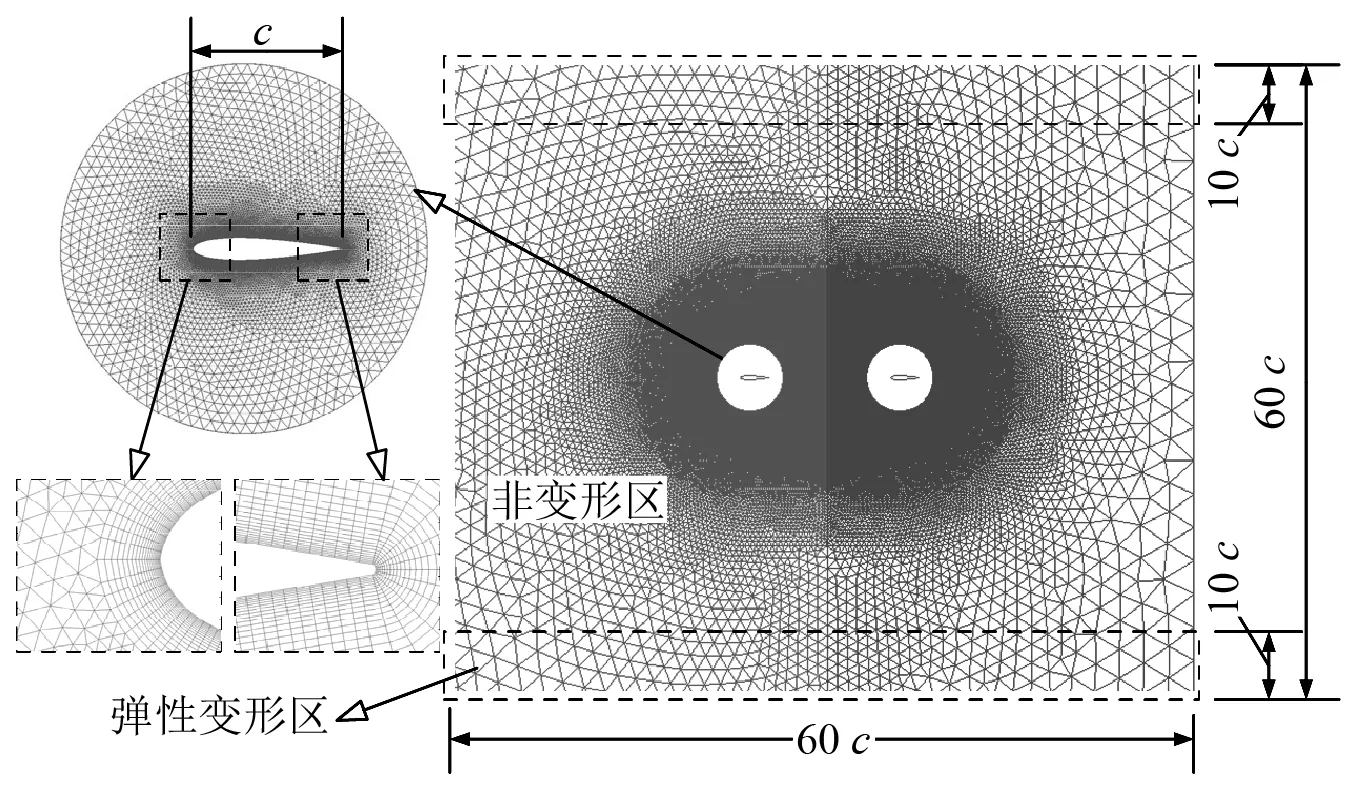
图1 计算域网格示意图Fig.1 Mesh arrangement details for dual-hydrofoil

前后两水翼的布置和相关参数设置，如图2所示。来流速度为U∞，两翼在x方向上的间距为Lx，平衡位置在y方向上的间距为Ly。 当水翼处于平衡位置时，俯仰角达到最大值为θ0。

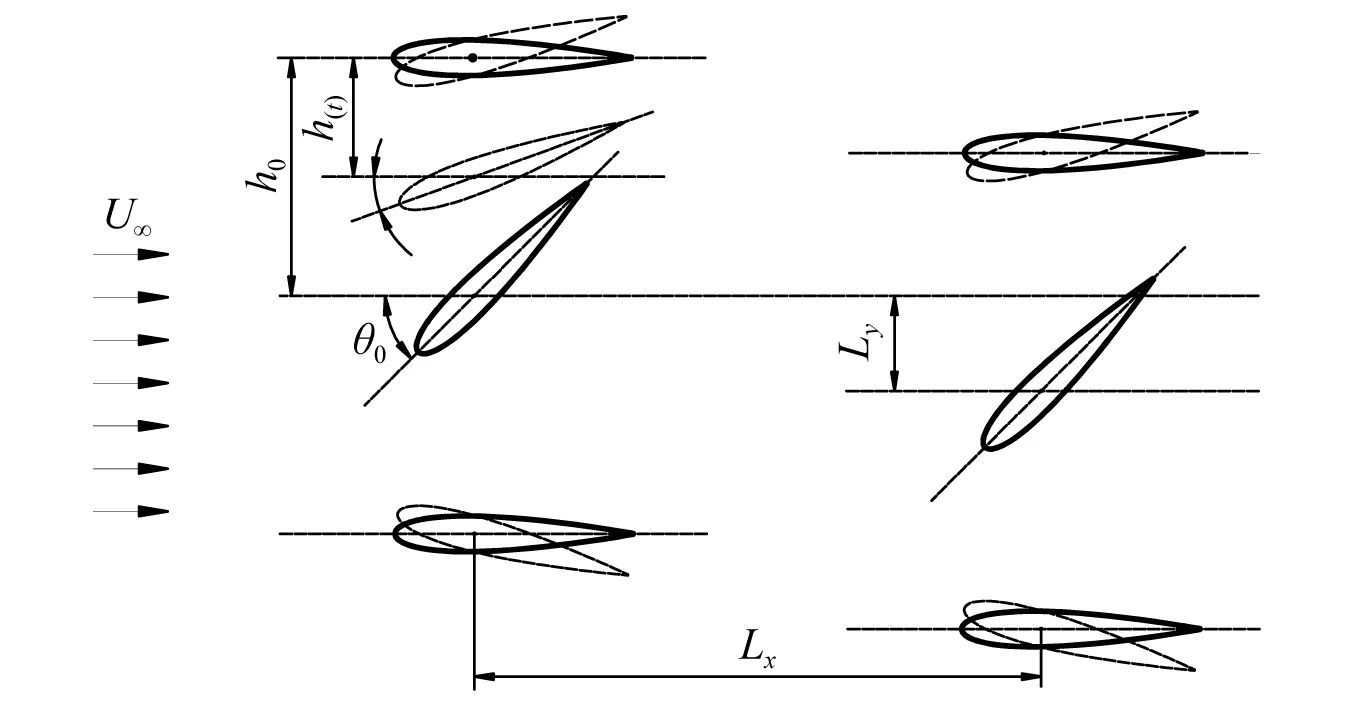
图2 前后两翼布置情况图Fig.2 Tandem arrangement of dual-hydrofoils

1.4.2 时间步及网格收敛性验证

为避免网格疏密及时间步长对计算结果的不利影响，进行网格和时间步收敛性验证。上游水翼振荡时一个周期内的升力系数曲线变化，如图3(a)所示。分别取3种不同数量的网格进行比较，研究网格密度对获能结果影响，发现当网格数量为24万～50万时，升力系数时历曲线非常接近，平均获能功率和效率如表1所示。24万和50万的获能效率相差约为3.6%，而12万相较于两者偏差较大。为保证收敛速度和计算精度，选取网格数量为24万以上的网格计算时，研究结果对网格密度不再敏感。

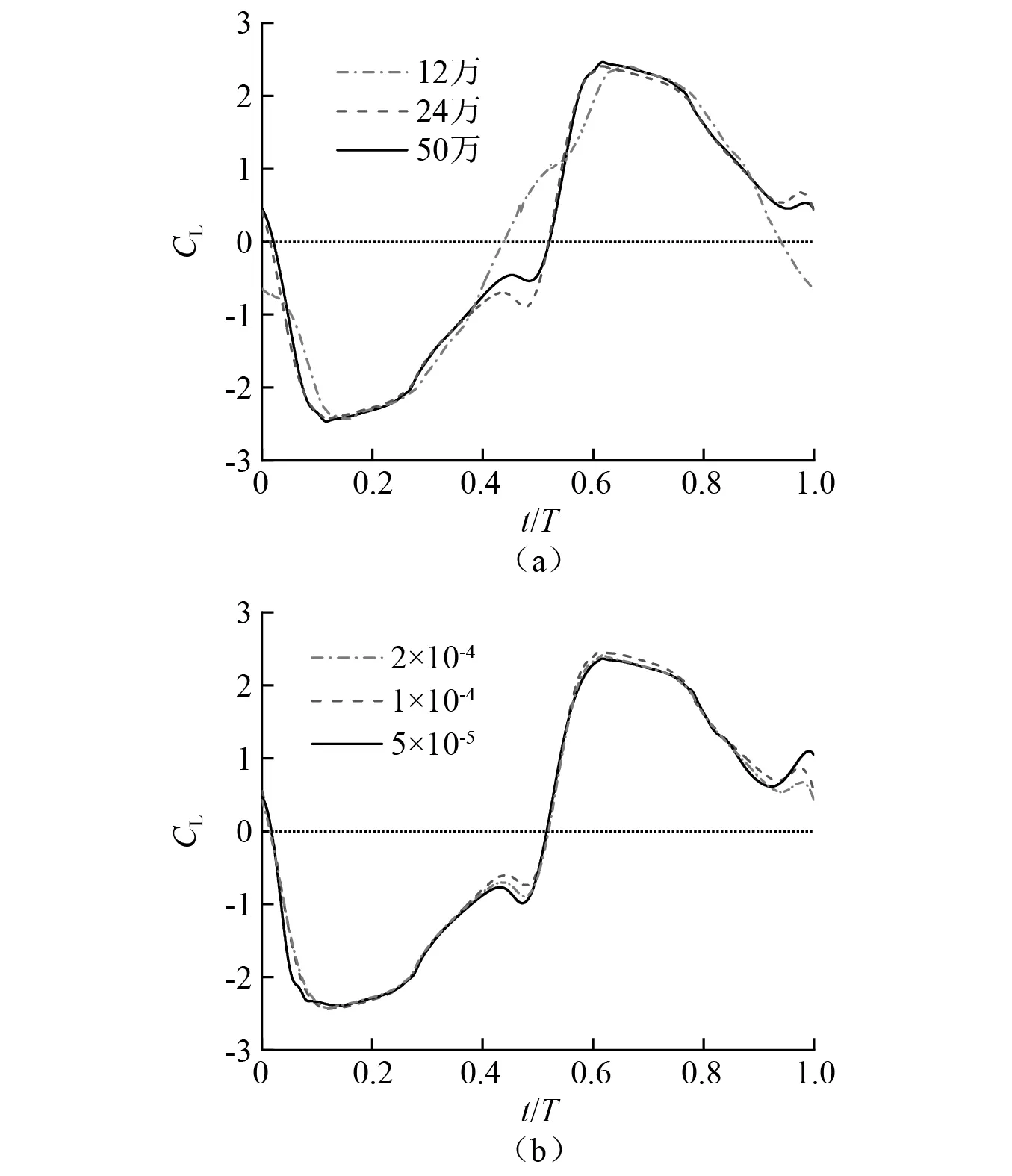
图3 网格及时间步收敛性验证对比图Fig.3 Convergence study of mesh resolution and time step

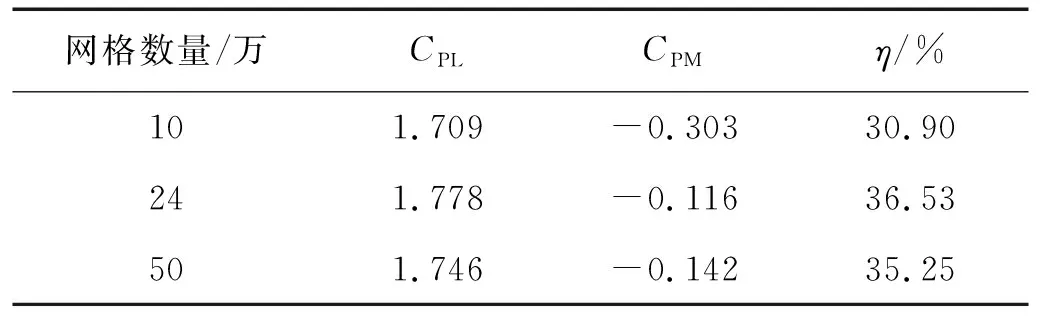
表1 不同网格数量结果验证Tab.1 Verifications of different mesh resolutions

保证库朗数小于1的条件下，取时间步长Δt分别为2×10-4s，1×10-4s，5×10-5s 3种工况进行计算，结果如图3(b)所示。可以看到3条升力系数曲线结果较为接近，对比表2中的获能情况，发现Δt=1×10-4s 与5×10-5s 间的误差仅为0.1%，为保证收敛速度和计算精度，文中取Δt=1×10-4s 的24万的网格进行数值模拟研究。

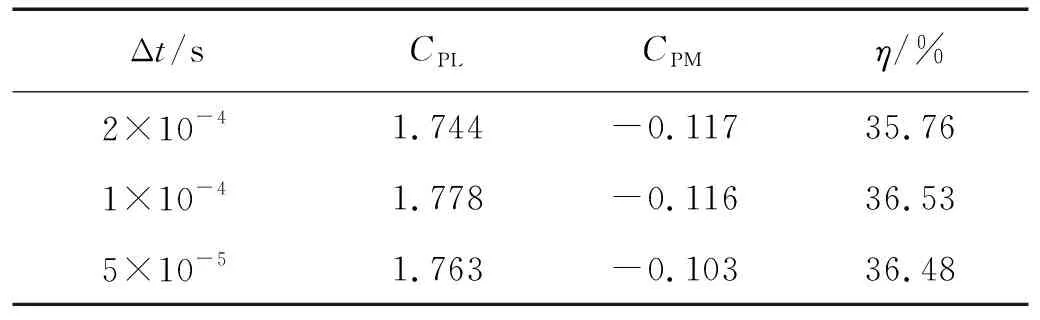
表2 不同时间步结果验证Tab.2 Verifications of different time steps

1.4.3 模型有效性验证

将计算结果与文献中相同工况的试验和数值结果进行对比，发现本文的结果比文献[16]中的数值结果更加接近文献[14]的试验结果，特别是在较小折算频率f*范围内(f*=fc/U∞，其中f为水翼的运动频率)，与试验结果吻合性更好。通过对比充分验证了本文数值模型的有效性。

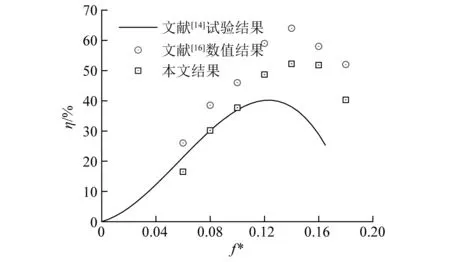
图4 与文献[14]试验及文献[16]结果对比图Fig.4 Comparisons with the results of experiments in reference [14] and reference [16]

2 研究结果与分析

2.1 前后水翼平衡位置相同时获能情况

本文主要针对NACA0015翼型进行研究，升沉振幅h0取值为1倍弦长，来流速度U∞取值为2 m/s，两翼间运动的相位差φ1-2=-π。采用总体相位Φ1-2来进行无量纲化处理，如式[15]所示

(15)

式中：Lx为两翼转轴之间的水平间距；φ1-2为两翼间运动相位差。

当Ly=0时双翼的获能情况，如表3所示。 因为在俯仰角幅值θ0≥75°时的涡脱落现象比较明显，所以上游水翼的俯仰角幅值θ0_1取值为75°； 由表3可知，在下游翼俯仰角θ0_2=75°、总体相位Φ1-2≈90°条件下，获能效率η高达52.24%，其中前翼为36.50%、后翼为15.74%，后翼仅为前翼获能效率的一半，占比较小。

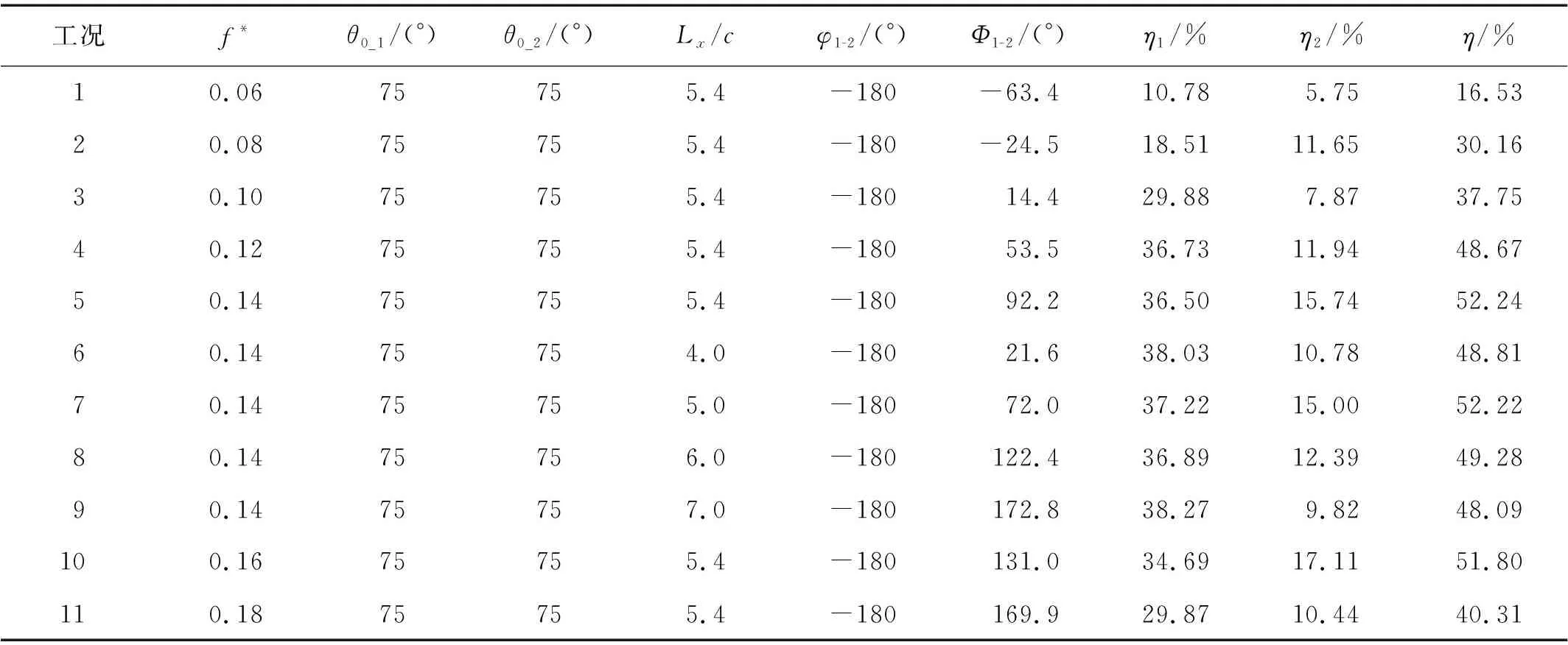
表3 串联双翼获能情况表Tab.3 Power extraction of the tandem hydrofoils

图5(a)给出了当f*=0.14时，间距Lx对双翼升力和力矩的平均获能功率影响； 图5(b)给出了当Lx=5.4c时，折算频率f*对双翼升力和力矩的平均获能功率影响。

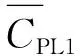
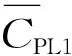
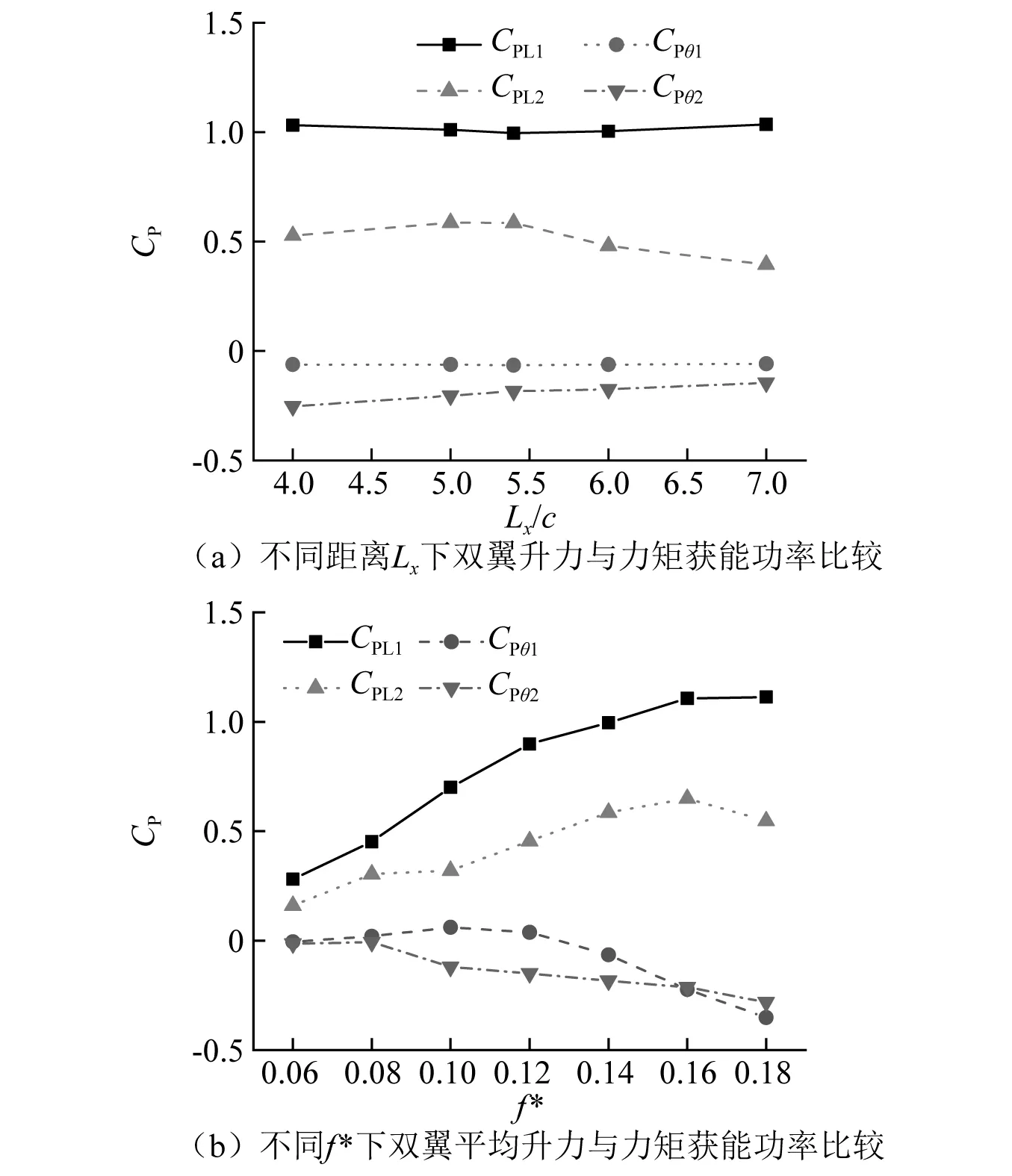
图5 不同参数影响下串联两翼的平均获能功率变化情况Fig.5 Power extraction versus different parameters for tandem hydrofoils

上述研究可以发现，通过改变运动参数和翼间布置可以大幅度影响水翼的获能功率，在保证全局相位位Φ1-2≈90°时，整个串联水翼系统的获能表现最优，这与Kinsey的研究结论一致。但也发现了后翼的获能功率依旧较低，当f*=0.14时仅为上游翼的43.12%，使得整个系统的获能功率并不高。在前翼运动、后翼静止的情况下，距离前翼转动中心分别取水平距离为3c和5c位置截面，给出其流向(x方向)速度分布规律，如图6所示。

由图6可知，当距离x取值为3c和5c时，前方水翼下游的过流断面尾迹平均流速还未得到均匀恢复，在振荡水翼平衡位置一倍弦长范围内，流动方向的平均流速仅为1.3 m/s，仅占上游翼来流能量的27.5%，尽管后翼在合适相位差条件下可以从前翼尾涡中提升获能效率，但是依旧有限。同时发现受上游翼的绕流影响，前方水翼尾流场中径向方向两倍弦长以外的区域流速约有5%的小幅度增加，因此用前后串联水翼的错位排列，改变前后振荡双翼的平衡位置，研究纵向间距对获能功率的影响，可以更好地提升双翼系统的获能效果。

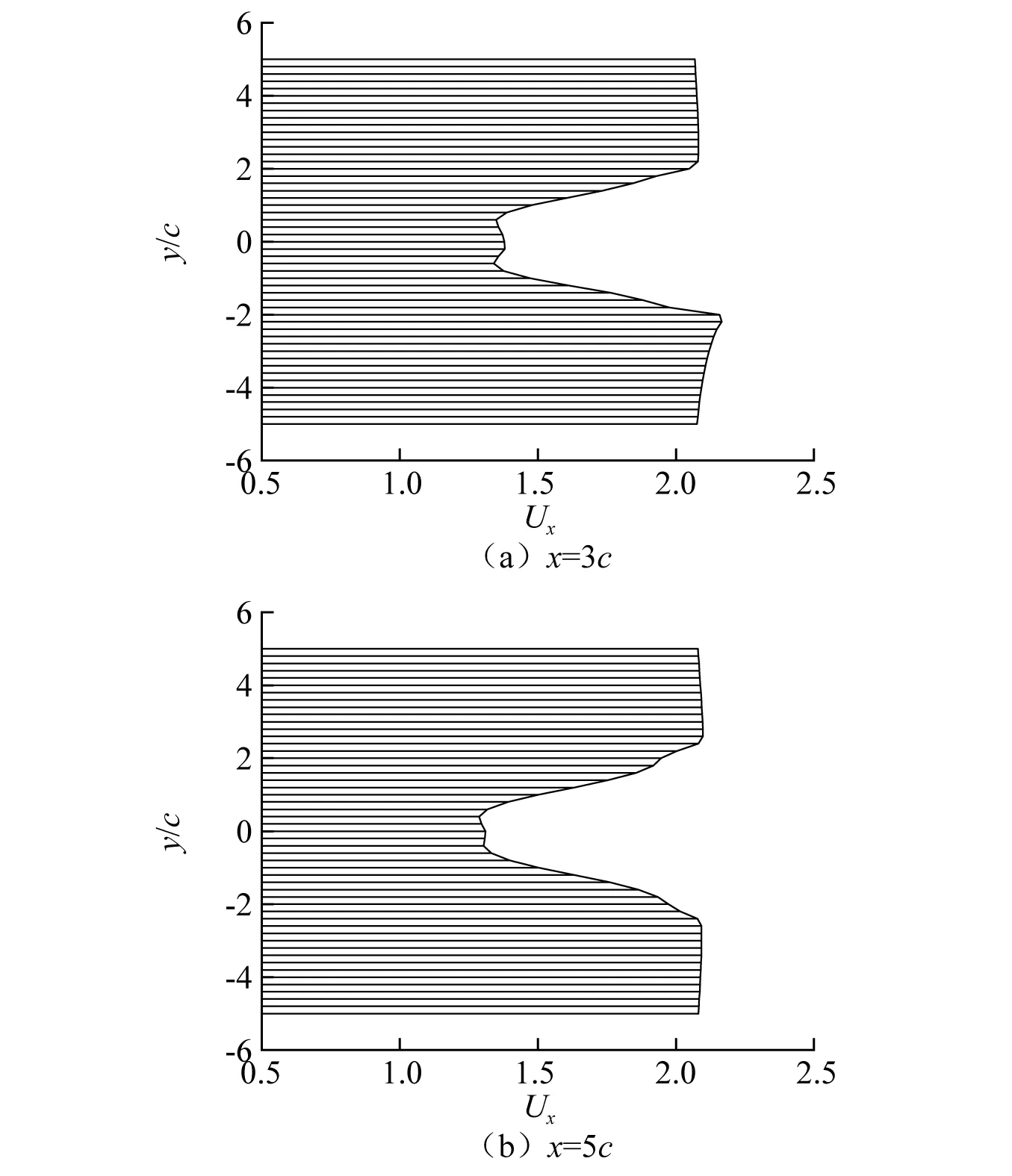
图6 不同距离时下游x方向流速分布情况Fig.6 Distribution of velocity in x direction

2.2 前后水翼错列时获能情况分析

改变径向(y方向)上前后两翼平衡位置距离Ly，此时两翼的运动参数取值为：h0=1c，θ0=75°，f*=0.14，Lx=5.4c。研究前后翼的纵向间距Ly对下游水翼获能的影响规律。计算得到的水动力系数曲线及功率获取情况，如表4所示，将这些结果与单翼独自振荡运动的获能不受上游影响的情况进行对比。

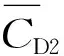
表4 不同Ly时下游翼获能功率及效率情况Tab.4 Power extraction of downstream hydrofoil with different Ly

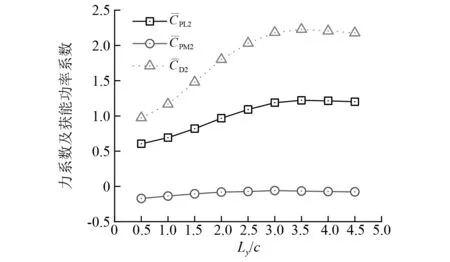
图7 力系数及获能功率系数随Ly变化曲线Fig.7 Force and power extraction coefficients versus Ly

不同Ly时一个周期内力系数变化图及功率获取情况图，如图8所示。下游翼不同Ly平衡位置的涡量图，如图9所示。图8(a)给出了一个周期内阻力系数CD2的变化情况，发现Ly=1.0c时，两个峰值都较低，结合图5中的速度分布情况可知，因后方水翼区域的来流速度普遍低于前方水翼来流速度，所以后翼的阻力系数偏低；当Ly=2.0c时，发现阻力系数的第一个峰值有非常明显的提升，此时水翼处于前翼尾涡区域，在后翼运动的前半个周期内，阻力值增加明显，但是在后半个周期内水翼向下运动时，未受到涡的影响，阻力峰值减小。当Ly继续增加时，结合图5，后翼的迎流范围逐渐远离低速区，两个峰值处趋于平稳。受到前翼尾涡的影响， 当Ly=3.5c时在第一个峰值处的峰值比第二个峰值有所提高。

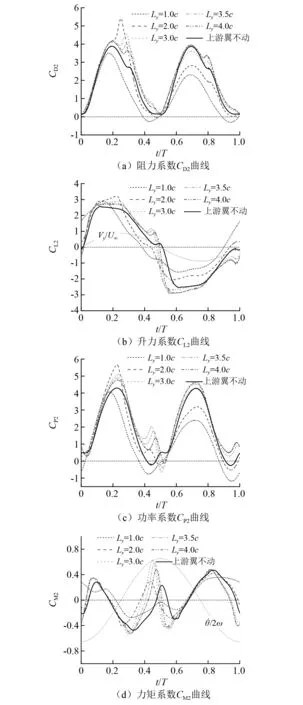
图8 不同Ly时一个周期内力系数变化图及功率获取情况图Fig.8 Forces and power coefficient over one cycle versus Ly

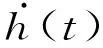
图8(d)展示了力矩系数CM2的变化情况，同时给出了无量纲化水翼转动的速度变化曲线。可以看到当Ly增加时，在t=0.4T～0.5T时的峰值逐渐增加，对应图9中涡量图看到Ly=2.0c，Ly=3.5c时前缘涡运动到水翼尾缘处产生负压，使力矩方向为逆时针，保证了水翼所受力矩与转动速度方向一致，此时力矩做正功，在Ly=3.0c时峰值达到最大，同时整体的力矩获能功率也达到最佳，图8(c)中总获能功率曲线在t=0.4T～0.5T时也因此得到了增加。

图9 下游翼不同Ly平衡位置时的涡量图Fig.9 Vortex topology evolution with different balanced position

为进一步说明振荡水翼在前翼尾涡影响下的水动力情况，图10分别为单翼振动和前翼运动影响下(Ly=3.0c)后翼在t=0.49T时刻，水翼的上、下表面压力系数分布情况。从图10(a)中可以看到，此时后翼前缘出现的脱落涡正沿着翼身向后缘移动，上表面的脱落涡处产生大范围的负压区域(约0.5c～0.9c处)，压力系数谷值达-3.5，此时水翼的升力系数稍大于零(见图8(b)，t=0.49T时刻区域)。

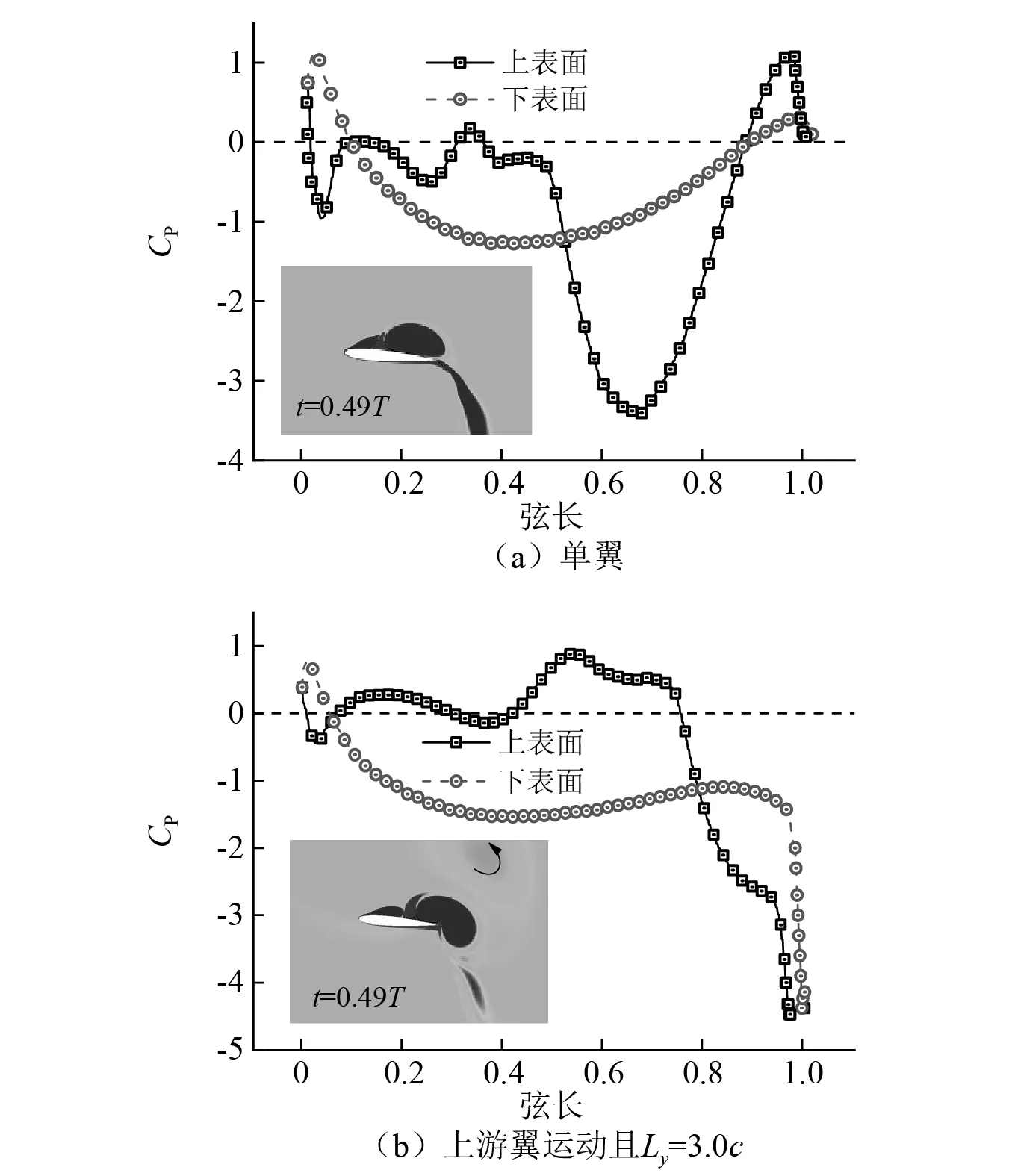
图10 当两种情况下t=0.49T时翼表面压力 系数分布及涡量图Fig.10 Distribution of pressure coefficient and vorticity fields in two situations at t=0.49T

对于Ly=3.0c的情况，受上游尾迹逆时针涡的影响，加速了后翼上的涡脱落，涡在t=0.49T时刻已运动至后翼尾缘并将离开翼身，此时在上翼面中部出现正压，靠近尾缘处出现巨大负压(约在0.8c～1.0c处)，压力系数谷值约-4.5。升力方面：随着涡提前离开翼身，水翼迅速失去向上的升力，升力方向改变，使得升力与升沉速度方向产生了更好的同步性，见图8(b)；力矩方面：由于上表面尾部的负压力，产生力矩方向为逆时针与俯仰运动方向一致，提高了力矩获能，见图8(d)所示。由此综合升力和力矩获能的改善，后翼总体获能得到了提升。

3 结 论

本文基于计算流体软件OpenFOAM对NACA0015翼型的串联式振荡翼进行了数值模拟研究，采用双翼错列分布的形式，着重分析了水翼纵向间距对双翼获能的影响，得到以下结论：

(1) 双翼串联条件下，前翼和后翼间的全局相位Φ≈π/2时，总获能效率最大。下游翼获能效率较低，不足上游翼获能的一半。

(2) 采用错位排列的方式可以有效提高后翼获能表现。根据双翼间过流断面的流速分布特点，前、后两翼平衡位置的纵向距离Ly取值为3.5c时，后翼的获能效率可达45.33%，相比于单翼的情况可以提升20.05%，是Ly=0时获能效率的近3倍，提升效果明显。

(3) 前翼的尾涡可以对后翼的获能产生积极影响。错位排列时，上游翼的尾涡在流经后翼时，改变了后翼前缘涡脱离的位置和时间点，对上翼面的压力分布产生了重要影响，使升力与升沉速度之间以及力矩和俯仰运动之间的同步性更佳，提升了水翼获能表现。