垂直振动下二元混合颗粒分离的影响因素及能量分析

刘 瑜， 周甲伟， 荆双喜， 罗晨旭

(1.河南理工大学 机械与动力工程学院，河南 焦作 454000； 2.河南牧业经济学院 能源与智能工程学院，郑州 450046) 3.华北水利水电大学 机械学院，郑州 450045)

颗粒物质广泛存在于自然界中，与日常生活密不可分。在农业、建筑业、运输业等领域，颗粒物质都起着很重要的作用，而且很多自然现象，如沙尘暴、山体滑坡、雪崩等都与颗粒物质的特殊性质有关[1-3]。

颗粒物质不同于传统的固体、液体和气体，具有独特的物理机械特性。比如“粮仓效应”，颗粒物质装入容器内，容器底部的压力最终会趋于一个定值[4-5]；“巴西果”“反巴西果”效应，不同颗粒混合后，经过振动，会出现大颗粒在上小颗粒在下的“巴西果”现象，或者大颗粒在下小颗粒在上的“反巴西果”现象[6-11]；还有“历史效应”、崩塌、偏析、斑图等现象[12-13]。研究颗粒运动的内在机理，揭示颗粒相互作用对宏观现象的影响规律，对工业发展和自然灾害防治等具有重要意义，一直是国内外学者的重要研究方向。

在垂直振动下，颗粒系统表现为复杂的聚合和分离行为。多年来，学者们试图采用试验和数值模拟的方法对颗粒在振动作用下的分聚行为进行研究，以揭示颗粒系统内在的分离机理。彭亚晶等[14]通过“巴西果”分离效应试验发现振动加速度存在一个临界值，影响分离效果。姜泽辉等[15]在试验过程中发现在一定条件下，颗粒床会出现“三明治”状态的分层结构。梁宣文等[16]在试验研究中观测到巴西果、反巴西果和三明治结构的动态循环反转。何菲菲等[17]发现同样的3种结构周期循环变化，并且三明治结构占据较长的周期时长。Xu等[18]指出在不同控制参数下，二元等厚颗粒混合物会出现5种分离模式，包括巴西果、反巴西果、混合状态、轻度巴西果和轻度反巴西果。Cano-Pleite等[19]通过试验研究了振动强度和气体速度对密度诱导颗粒分层的影响规律。赵永志等采用离散单元方法模拟巴西果效应分离过程，指出振动分离过程中存在最优的振幅和频率。Dai等[20]提出一种新的分离指标并采用离散单元法(discrete element method， DEM)对该指标进行了验证。Qiao等[21]采用DEM对巴西果分离中分离度和大颗粒上升速度的影响因素进行研究。赵啦啦等[22-24]用DEM方法研究振动模式、颗粒形状和干湿颗粒对分层行为的影响规律。众多研究表明，采用离散单元法进行数值模拟研究，参数的选择是影响颗粒分离效果的重要因素。

本文采用离散单元法对二元混合颗粒垂直振动下的分离行为进行模拟，研究接触刚度、摩擦因数和振动空间对分离效果的影响，并试从能量的角度揭示其分离机理。

1 离散单元法

离散单元法通过模拟系统内部颗粒间的受力和运动行为，揭示颗粒系统宏观力学特性的细观机理，是研究颗粒物质力学特性的重要数值模拟方法。离散单元法的核心是颗粒间的接触模型，接触模型对应于不同的颗粒特性，决定了数值模拟结果的可靠性。

目前常用的颗粒接触模型包括线性模型、黏结模型、平行黏结模型、赫兹模型等，本文主要研究颗粒运动分离行为，不考虑颗粒间的黏结作用，采用常规线性模型。

2 二元混合颗粒数值模拟试验

2.1 试样制备和模拟参数

建立长方体振动床，长度和宽度都为5 cm，高为30 cm。振动床内部填充二元混合颗粒，粒径分别为5 mm(大颗粒)和2.5 mm(小颗粒)，二者的质量相同，大颗粒的密度为400 kg/m3，小颗粒的密度为3 200 kg/m3。大小颗粒的体积比为1∶1，颗粒总数为4 000，其中大颗粒445个，小颗粒3 555个。本文分别对3种接触刚度(K=500 N/m，1 000 N/m，2 000 N/m)、3种摩擦因数(f=0.1，0.3，0.5)以及3种振动空间(无挡板、挡板距底面0.5 m和挡板距底面0.4 m)进行了数值模拟，研究各因素对分离效果的影响规律。

2.2 试验过程及分离效果定量描述

在振动床内随机生成大小颗粒，并依靠重力作用落至振动床底部，得到二者充分混合的初始平衡状态，如图1(a)所示。统计颗粒的堆积空间，得到初始平衡状态堆积高度为3.4 cm。为使振动分离达到较好的效果，选择赵永志等的研究确定的振动频率60 Hz，振幅0.6 cm进行数值模拟。通过改变颗粒之间的接触刚度、摩擦因数和挡板至振动床底的距离，对颗粒的振动分离效果进行研究。数值模拟过程中，分别记录振动床底层、中层和上层的大颗粒、小颗粒的Z轴方向位置以及大小颗粒的总体动能变化。

采用Lacey 混合指数[25-27]定量描述二元混合颗粒体系的分离程度。对于均一粒径体系，Lacey混合指数表示为

(1)

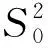
(2)

(3)

式中：p，q分别为两种颗粒的体积含率;N为样本内平均颗粒数量。

对于本文研究的二元颗粒体系，采用赵永志等研究中的 “等效颗粒数量”的方法确定N，计算二元颗粒的实际混合方差。

3 数值模拟结果分析和讨论

3.1 振动分离过程

二元球形颗粒在振动床内振动分离过程如图1所示。0时刻为颗粒自由下落后的初始平衡状态，颗粒体系的Lacey混合指数为0.96，大小颗粒混合充分。施加正弦垂直振动载荷，颗粒开始运动。1 s时，大颗粒开始向振动床上层移动，颗粒体系的Lacey混合指数为0.81；5 s时，有更多大颗粒运动至振动床上层，颗粒系统的Lacey混合指数为0.48，颗粒系统已经能够分离出半数左右的颗粒；10 s时，可以观察到明显的大颗粒在上、小颗粒在下的分离效果，此时颗粒系统的Lacey混合指数为0.38；到30 s时，大小颗粒的分离效果更好，颗粒系统的Lacey混合指数为0.29。

图1 振动分离过程中颗粒的瞬态图(f=0.1, K=1 000 N/m，无挡板，堆积高度3.4 cm)Fig.1 Particle transient figure of vibration segregation procedure (f=0.1, K=1 000 N/m，no baffle, stack height 3.4 cm )

3.2 接触刚度对分离的影响

在其他参数均相同的条件下，对500 N/m，1 000 N/m和2 000 N/m 3种接触刚度的振动分离效果进行数值模拟。

图2是3种接触刚度分离过程中颗粒平均动能的变化曲线。从图2可以看出，颗粒分离过程中，小颗粒的平均动能大于大颗粒的平均动能。这说明，在振动过程中，小颗粒比较活跃，更容易填充至下方的空隙中，从而逐渐托举起大颗粒。随着颗粒接触刚度的增加，颗粒的平均动能呈现增大的趋势，这与线性接触模型中接触力的计算方法相一致。

图2 不同接触刚度下颗粒平均动能变化曲线Fig.2 Variation curve of particle average energy with different contact stiffness

图3为3种接触刚度下，颗粒系统的Lacey混合指数变化曲线。接触刚度为500 N/m，1 000 N/m和2 000 N/m时，颗粒系统在30 s内的Lacey混合指数分别达到了0.26，0.29和0.36，都有较好的分离效果。特别是接触刚度为500 N/m时，分离效果最好。从图3可知，Lacey混合指数随接触刚度的增加有缓慢增加的趋势，即增大接触刚度，将使得颗粒系统的分离效果降低。

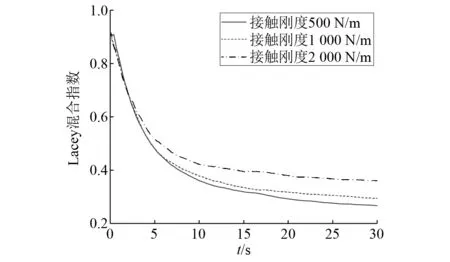
图3 接触刚度对分离效果的影响Fig.3 Influence of contact stiffness on segregation effect

3.3 摩擦因数对分离的影响

保持其他参数相同，将摩擦因数分别设置为0.1，0.3和0.5，得到3种摩擦因数下的Lacey混合指数随时间的变化曲线，如图4所示。从图4可以看出，随摩擦因数的增加，颗粒系统的Lacey混合指数呈增加趋势。当摩擦因数为0.5时，Lacey混合指数在0.9上下波动，颗粒系统无法实现分离。

图4 摩擦因数对分离效果的影响Fig.4 Influence of friction coefficient on segregation effect

通过检测颗粒圆心所在位置，选择初始平衡时位于振动床顶层的2颗小颗粒和位于振动床底层的2颗大颗粒，监测振动过程中颗粒距振动床底部的距离。考虑颗粒的接触情况，小颗粒I和大颗粒I都靠近振动床中部，小颗粒II和大颗粒II都靠近振动床侧壁。监测结果如图5所示。

从图5(a)和5(b)可以看到：当摩擦因数为0.1和0.3时，顶层小颗粒大多数时间在距底面0.02 m以下；当摩擦因数为0.5时，顶层小颗粒距床底的距离呈现近似周期运动，平衡位置在0.020～0.025 m，振幅大约为0.02 m。图5(c)和5(d)中大颗粒距床底的距离统计表明，当摩擦因数为0.1和0.3时，底层大颗粒大多数时间的位置在距底面0.02 m以上，大颗粒的运动位置明显要高于小颗粒的运动位置，从而实现了二者的分离。当摩擦因数为0.5时，底层大颗粒也呈现近似周期运动，平衡位置和振幅都与小颗粒的运动情况类似，致使大小颗粒一直处于充分混合状态。

图5 不同初始位置颗粒距振动床底的高度变化Fig.5 Distance to the variation bed bottom of particles at different initial positions

更进一步研究，选取在振动床底层、中间和顶层的大、小颗粒各8颗，图6为16颗大小颗粒在振动过程中距离振动床底的平均距离对比。从图6可以明显看出，当摩擦因数为0.1和0.3时，小颗粒和大颗粒距床底的平均距离差值较大，利于实现二者的分离；而当摩擦因数为0.5时，小颗粒和大颗粒距床底的平均距离很接近，大小颗粒分离困难。这与图5中监测颗粒运动轨迹得到的结论一致。

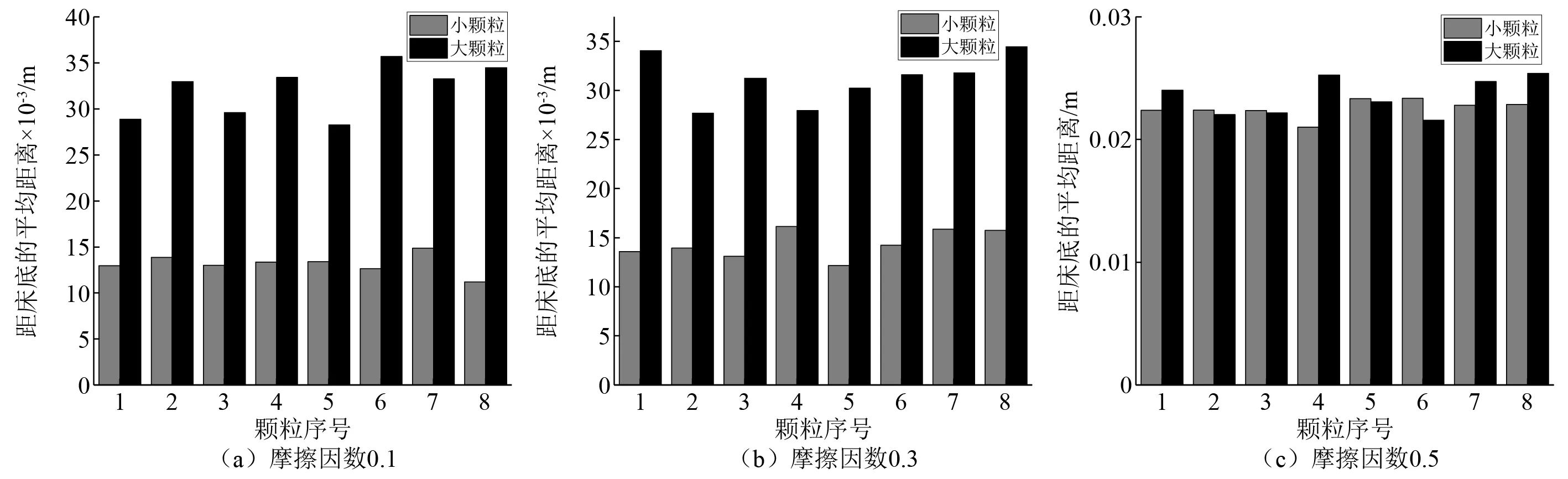
图6 大小颗粒距振动床底的平均距离对比Fig.6 Comparison of distances to the variation bed bottom between big and small particles

结合图5和图6可知，颗粒可以实现分离时，小颗粒距床底的平均距离小于0.02 m，而大颗粒距床底的平均距离大于0.02 m。因此，以0.02 m为分界线，每隔0.1 s记录16颗大小颗粒距振动床底的距离，并统计30 s内被监测各小颗粒距床底距离小于0.02 m，各大颗粒距床底距离大于0.02 m的概率，结果如表1和表2所示。

表1 小颗粒距床底距离小于0.02 m的概率Tab.1 Percentage of the data less than 0.02 m in all statistical data (small particles) %

表2 大颗粒距床底距离大于0.02 m的概率Tab.2 Percentage of the data more than 0.02 m in all statistical data (large particles) %

对比表1和表2中的数据：当摩擦因数为0.1时，在模拟的30 s内，大颗粒平均有80%的时间在颗粒床上层振动，小颗粒平均有83%的时间在颗粒床下层振动，大小颗粒混合区域较小，大小颗粒容易实现分离，Lacey混合指数低于0.3；当摩擦因数为0.3时，大颗粒平均有91%的时间在颗粒床上层振动，小颗粒平均有56%的时间在颗粒床下层振动，说明在振动过程中，小颗粒的位置不确定性大，会有一半的时间在颗粒床上层，大小颗粒在上层混合，导致较难实现分离，Lacey混合指数只能达到0.4；当摩擦因数为0.5时，大颗粒平均有58%的时间在颗粒床上层振动，小颗粒平均有45%的时间在颗粒床下层振动，这说明振动过程中大小颗粒的位置都不确定，大颗粒会频繁出现在颗粒床下层，小颗粒会频繁运动至颗粒床上层，这种不确定性，导致颗粒无法实现分离，Lacey混合指数一直在0.9左右波动。

图7为不同摩擦因数时颗粒平均动能变化曲线，从图7可知：颗粒平均动能随着摩擦因数的增大出现先减小又增大的规律；当摩擦因数为0.3时，颗粒平均动能峰值平均值最小；当摩擦因数为0.5时，颗粒平均动能峰值平均值最大。

图7 不同摩擦因数时颗粒平均动能变化曲线Fig.7 Variation curve of particle average energy with different friction coefficients

颗粒间摩擦因数对颗粒的运动起抑制作用。当摩擦因数较小时，颗粒之间会出现明显相对滑动，但是摩擦力(即剪切力)较小，颗粒垂直上下振动占主导作用，因此颗粒平均动能较大。随着摩擦因数的增大，颗粒之间发生相对滑动的阻碍增大，但是在特定数值模拟条件下，颗粒之间仍然有很多产生了相对滑动，此时摩擦力(即剪切力)比之前有所增加，抑制了颗粒垂直方向的运动，使得颗粒的平均动能出现减少的趋势。摩擦因数进一步增大，到0.5时，颗粒间较难产生相对滑动，这种情况下，只有少数颗粒会产生相对滑动，相比之前两种情况，摩擦力(即剪切力)对颗粒垂直方向运动的影响较小，所以颗粒具有较大的垂直方向速度，颗粒的运动出现与振动载荷相似的规律，此时颗粒平均动能出现增加的趋势。

3.4 振动空间对分离的影响

由图5可知，颗粒振动过程中距床底的最大距离都小于6 cm。考虑振动空间对分离的影响，当摩擦因数为0.1，接触刚度为1 000 N/m时，在距床底5 cm和4 cm处设置挡板，得到图8所示的Lacey混合指数变化曲线。

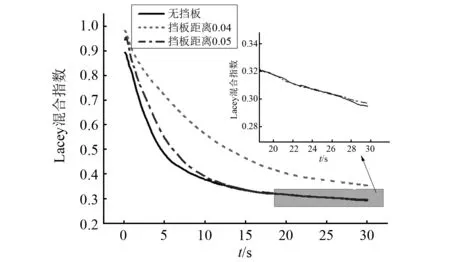
图8 不同振动空间Lacey混合指数变化曲线Fig.8 Variation curve of Lacey mixing index with different variation spaces

图8表明，挡板距离为4 cm时，颗粒向上运动受到挡板影响，颗粒的分离效果明显下降，挡板距离为5 cm时颗粒的分离效果与无挡板相比较差别不大。由图5中实线可知，被监测的大小颗粒距床底距离高于5 cm比例不大，颗粒运动过程受挡板影响较小，对颗粒分离效果影响较小。

在初始平衡状态，计算得到振动床的堆积高度为3.4 cm。模拟结果表明，当振动空间和颗粒体积比大于1.5时，颗粒分离效果较好，当振动空间和颗粒体积比为1.2时，颗粒分离效果明显减小。

3.5 颗粒动能变化对分离的影响

在研究中发现，振动床垂直振动过程中，大小颗粒的分离情况与二者的平均动能比值存在一定的联系，如表3所示。表3为不同模拟条件下，大小颗粒平均动能的比值R和30 s时的Lacey混合指数L。表3中:K为接触刚度；f为摩擦因数；D为挡板到床底的距离。

由表3可知 ，大颗粒平均动能都小于小颗粒平均动能，小颗粒更为活跃，更容易填充到空隙中，致使大颗粒无法回填到下层位置，从而逐渐移动至上层，并在上层附近振动。大颗粒平均动能约占小颗粒平均动能0.5～0.6时，颗粒床分离效果较好。大颗粒平均动能占比越大，大颗粒和小颗粒的相对活跃度越接近，此时大小颗粒会竞争填充至颗粒床下层，动能大的大颗粒可能优先填充至下层空隙中，导致小颗粒无法继续回填，从而增加颗粒分离的难度。

表3 大小颗粒平均动能比值对Lacey混合指数的影响Tab.3 Influence of average kinetic energy ratio of large particles to small particles on Lacey mixing index

4 结 论

分析颗粒床垂直振动时的分离过程，通过对动能、颗粒位置和Lacey混合指数的研究，明确接触刚度、摩擦因数和振动空间对分离效果的影响规律，得到以下结论。

(1)在颗粒振动分离过程中，颗粒间的接触刚度会影响振动分离的效果。随着接触刚度的增大，Lacey混合指数有增大趋势，颗粒分离效果有所降低。

(2)随着摩擦因数的增加，颗粒分离效果逐渐降低。当摩擦因数为0.1时，颗粒间的摩擦力较小，颗粒垂直振动的速度较大，颗粒的平均动能较大，此时小颗粒约有83%的时间在底层运动，大颗粒多数时间在上层运动，二者容易实现分离。当摩擦因数为0.3时，颗粒间相对滑动的摩擦力增大，颗粒垂直振动的速度减小，颗粒的平均动能减小，小颗粒回落困难，仅有56%的时间在下层运动，致使二者分离效果降低。当摩擦因数为0.5时，颗粒之间较难产生相对滑动，所有颗粒在振动床内都呈现近似从底层到顶层的周期运动，致使二者无法实现分离。

(3)振动空间减小，限制颗粒向上运动，会影响颗粒分离效果。当振动空间和颗粒体积比大于1.5时，颗粒分离效果较好，当振动空间和颗粒体积比为1.2时，颗粒分离效果明显减小。

(4)振动分离过程中，小颗粒的动能大于大颗粒动能，更容易填充下层空隙，将大颗粒托举至上层。大颗粒平均动能约占小颗粒平均动能的0.5～0.6时，颗粒分离效果较好。大颗粒平均动能与小颗粒平均动能接近时，小颗粒的填充机制难以发挥作用，致使二者无法实现分离。