时滞和扩散影响下社交网络谣言传播动力学*

王楠 肖敏† 蒋海军 黄霞

1) (南京邮电大学自动化学院&人工智能学院,南京 210023)

2) (新疆大学数学与系统科学学院,乌鲁木齐 830047)

3) (山东科技大学电气与自动化工程学院,青岛 266590)

提出了一个考虑空间扩散与发酵期时滞的社交网络谣言传播模型,重点研究了扩散与时滞对在线社交网络中谣言时空传播的影响.首先,分析了谣言传播平衡点的存在性,并得到了基本再生数 R0 ;其次,运用Roth-Hurwitz 稳定判据分析了谣言传播平衡点的局部稳定性,并讨论了扩散诱导的Turing 不稳定;最后,选取时滞为分岔参数,建立了谣言传播模型的Hopf 分岔条件.数值仿真结果表明,扩散和时滞的出现都能使得谣言传播模型的稳定性发生根本性改变.本文从时间和空间两个维度扩展了传统谣言传播动力学仅考虑时间演化的局限,更加真实地模拟了谣言在现实社会中的时空传播规律,为谣言传播的治理提供了全新的角度和思路.

1 引言

2022 年2 月,中国网民规模达10.32 亿,互联网普及率达73.0%,形成了全球最为庞大的数字社区.在线社交网络的发展一方面使得网民之间的交流变得更加便捷,另一方面也为谣言传播提供了新的途径[1-3].网络谣言传播比传统途径传播速度更快,范围更广,不加以阻断可能会在短时间内占用大量社会资源,引发民众恐慌甚至造成巨大的经济损失[4,5].特别是在突发性公共卫生事件中,由于民众对事件本身不了解,往往会被谣言和不实信息所吸引,甚至成为谣言传播者,极大地破坏了社会的稳定[6,7].因此,定性和定量地研究社交网络中虚假信息的传播规律,成为谣言治理工作的重中之重.

如何建立符合现实的社交网络谣言传播模型受到广大学者的高度关注.谣言在网络中传播具有隐蔽性强、传播范围广、传播途径复杂以及传播过程难以控制等特征,这与传染病在人群中扩散有着极大的相似.因此,谣言经常被称作互联网中的传染病.现有的网络谣言传播模型大多借鉴了传染病模型[8-10].例如,利用传染病动力学中仓室模型[11,12]的概念将社交网络中的人群区分为谣言易感者、谣言已知者和谣言恢复者等基本类型,并在SIR (susceptible-infected-recovered)模型的基础上建立起各类网络谣言传播模型.这些数学模型能够精准而直观地描述网络谣言的传播规律,充分而深刻地揭示网络谣言传播的危害.因此,基于传染病模型的谣言传播动力学已引起广泛关注.例如,Moreno 等[13]在2004 年首次研究虚假信息在随机无标度网络中的扩散过程,通过对参数时间分布的数值计算区分不同的谣言传播算法;Zhou 等[14]考虑网络拓扑结构及感染节点的邻近节点之间的差异对谣言传播的影响,发现感染节点的总数取决于网络的拓扑结构;张芳等[15]指出,谣言是一种典型的社会群体心理现象,在建立传播模型时应引入心理学因素,如感知、情绪、记忆、决策等;赵来军等[16]考虑了记忆因素对谣言传播过程的影响,提出了具有遗忘机制的谣言传播模型,并且发现网络的平均度存在阈值,超过这个阈值,谣言的影响就会达到饱和;顾亦然和夏玲玲[17]注意到重要熟人免疫策略能有效地抑制谣言传播,建立了新的SEIR (spreader-exposed-ignorant-recovered)谣言模型并根据真实在线社交平台Facebook 的用户数据进行数值模拟;万佑红和王小初[18]基于现实社交网络中存在的从众效应进行模拟仿真,研究个体影响力对谣言扩散的作用;朱霖河和李玲[19]在传统的网络谣言传播模型中引入饱和辟谣函数用以刻画政府辟谣行为对谣言传播的约束能力;Ruan 等[20]研究在简单传播模型里引入智能节点研究恶意节点对谣言传播的影响,结果表明恶意节点紧密度的增加会助长虚假信息的传播;Chen 和Wang[21]将谣言未知者按性格分为稳重型未知者和激进型未知者,提出了新的SEIsIrR (spreader-exposed-steady ignorantradical ignorant-recovered)谣言传播模型,通过对Twitter 上真实传播的谣言数据集进行仿真,证明人的性格、谣言的可信度及谣言与生活的相关性影响着谣言传播的范围与速度.

随着近些年移动互联网设备的迅猛发展,人们早已突破时空限制,可以随时随地通过社交网络参与到公共事件的讨论中.因此建立反应扩散方程[22,23]来描述网络信息的时空扩散变得具有现实意义.反应扩散网络谣言传播模型不仅能够反映谣言的网络分布特征,还可以描述其发展趋势: 扩散项刻画了网络谣言在一维空间中沿着某一固定传播方向进行扩散的过程;在传播方向上的某一固定空间位置内,网民自行传播谣言,由于位置不变,该过程与谣言传播的时间紧密关联.一些学者也建立了相应的反应扩散谣言传播模型,研究其丰富的时空动力学特征.例如,赵洪涌和朱霖河[24]针对媒体报道与空间扩散等因素,建立了反应扩散SIM (spreader-ignorant-medium)谣言传播模型,并给出系统稳定与Hopf 分岔产生的条件;Zhu 等[25]为了使得模型更加贴合真实的传播机制,在反应扩散SI(spreader-ignorant)谣言传播模型中加入非线性发生率βSI/(1+αI),并分析了扩散系数对谣言传播稳态的影响.

在实际的网络谣言传播过程中,时间滞后同样不可忽视.在网络谣言从产生、传播、治理到消失的各个阶段中都可能存在着时滞[26,27].谣言刚出现时一般只在小范围内传播,但借助开放的社交网络,其在人群的讨论中酝酿发酵,甚至会在更大范围内传播.发酵期时滞指的是网络谣言从产生到传播的过程中会在谣言易感者群体中存在时间滞后的现象,忽视谣言传播的发酵期可能会导致谣言治理的不及时.

但是目前同时考虑空间扩散效应与发酵期时滞的谣言传播模型并不多见.为了更好地刻画不同人群在谣言传播模型中相互转化的过程,本文考虑在谣言传播过程中谣言未知者会以不同类型的发生率分别转化为谣言感染者及恢复者,并且谣言感染者会在社交网络中接收到辟谣信息从而转化为恢复者.基于上述分析,从时空维度建立一个具有饱和发生函数、发酵期时滞以及扩散项的谣言传播模型,研究时滞与扩散项对谣言传播模型稳定性的影响.

本文结构组织如下.在第2 节中,提出一个具有扩散效应和时滞的谣言传播模型.在第3 节中,对模型进行稳定性分析,并研究无时滞反应扩散谣言传播模型的Turing 不稳定性.选取时滞为分岔参数,给出了模型在平衡点处发生Hopf 分岔的条件.在第4 节中,通过数值仿真来验证前文的理论结果.在第5 节中,对本文工作进行总结并展望未来的工作.

2 模型建立

文献[10]将网民分为谣言未知者S、谣言已知者I和谣言恢复者R这三种状态,其描述的SIR谣言传播模型如下:

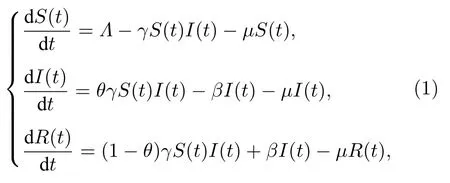
其中,未知者S未收到谣言,已知者I收到谣言并传播,恢复者R收到谣言但不传播.由于社交网络具有开放性,未知者S以Λ的人口输入率自然增长,γ表示谣言在社交网络上传播的速率,接触到谣言的未知者S以θ和 1-θ的概率分别转为已知者I和恢复者R,辟谣信息以β的速度在社交网络中传播.同时三种状态的网民均以µ的概率离开.考虑现实意义,以上参数均为正.文献[10]通过计算给出了模型(1)的平衡点和基本再生数R0的表达式,讨论该模型的稳定性和分岔点,并通过几何方法分析了局部平衡点的全局稳定性.仿真结果表明,模型(1)在R0=1 处存在分岔,并且当R0＞1时,已知者I密度随着R0的增加而逐渐增加;θ的变化对稳定状态下I密度的峰值有较大影响,但对I密度的收敛时间影响较弱.这为谣言治理工作提供了新的思路.

然而模型(1)没有考虑扩散和时滞对于网络谣言传播的影响.为了使模型更加贴合现实,我们在模型(1)的基础上引入扩散项、时滞与饱和发生率.文献[19]提出用饱和函数h(I)=βI/(1+αI)来描述辟谣信息在社交网络中的传播,其中β表示辟谣信息在社交网络上的传播速度,α是衡量已知者种群数量对于辟谣信息传播效果的饱和因子,这与现实中网络谣言的传播规律十分贴合.于是得到了以下具有饱和函数的时滞反应扩散谣言传播模型:

其中t＞0,x∈Ω=(0,π) .初始条件为

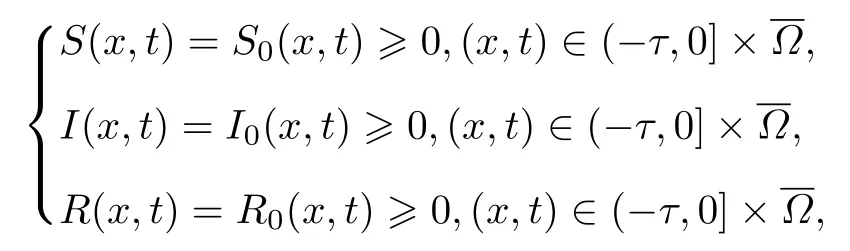
Neumann 边界条件为

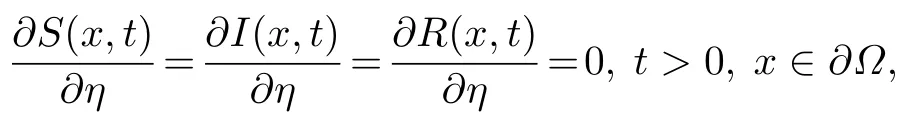
S(x,t),I(x,t)和R(x,t) 分别表示谣言未知者、谣言已知者和谣言恢复者在t时刻x位置处的密度.γS(x,t-τ)I(x,t)表示谣言已知者I在谣言未知者S种群中传播谣言的能力,τ是谣言未知者S种群在接收到谣言后经过讨论和思考而决定是否传播谣言的反应时间.βI(x,t)/(1+αI(x,t)) 是辟谣信息在谣言已知者I数量的饱和作用下将谣言已知者I转化为谣言恢复者R的辟谣能力.初始条件S0(x,t),I0(x,t)和R0(x,t)为非负连续函数.Δ=∂2/∂x2是拉普拉斯算子.d1＞0,d2＞0 和d3＞0分别是S(x,t),I(x,t)和R(x,t) 的空间扩散系数.Ω是一个有界域,∂Ω是Ω的光滑边界,η是∂Ω的单位外法向量.Neumann 边界条件表示谣言传播系统是封闭的,谣言在网络边界没有流进与流出.

3 时空动力学分析

根据现实意义,本文研究模型(2)的两个非负平衡点:

(i)无谣言平衡点E0=(Λ/µ,0,0),此时模型(2)中仅存在谣言易感者,谣言未能在人群中传播;

(ii)谣言传播平衡点E*=(S*,I*,R*),此时存在谣言传播者,谣言已在人群中持续传播,其中

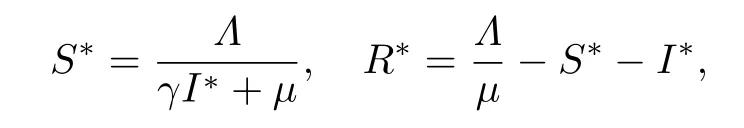
并且I*满足方程

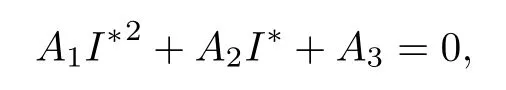
其中

假设:

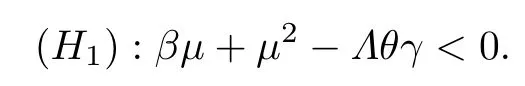
当 (H1) 成立时,则有

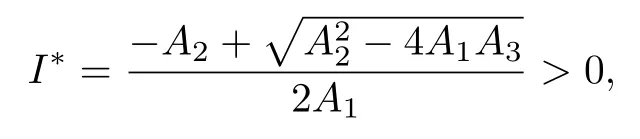
此时E*=(S*,I*,R*) 为模型(2)的唯一正平衡点.

基本再生数R0是谣言传播模型中一个重要参量,用于衡量网络谣言在人群中传播扩散的能力.当R0＜1 时,谣言在人群中会自行消亡;当R0＞1时,谣言则会持续存在下去.本文根据文献[28]的再生矩阵的方法计算R0.令X=(i,r)T,不考虑扩散项,由模型(2)可得

其中,

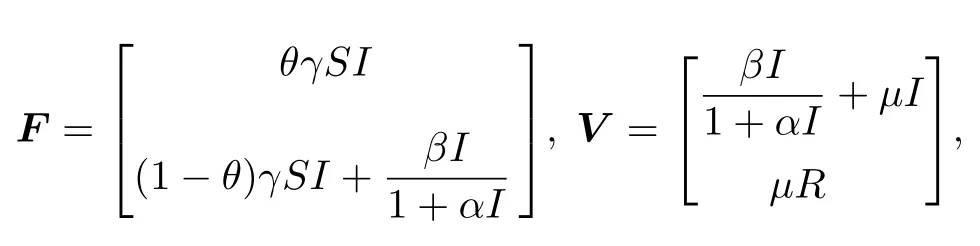
在无谣言平衡点E0处的雅克比矩阵分别为

于是有

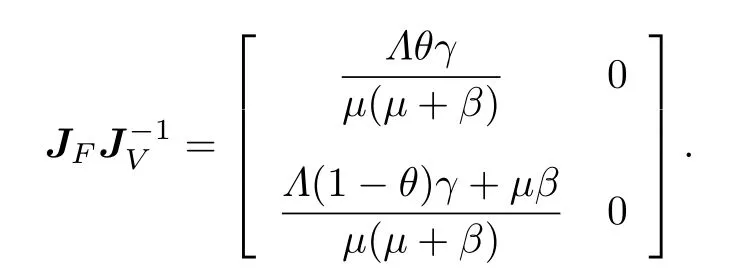
令

则模型(2)的线性化系统为

其中

并且

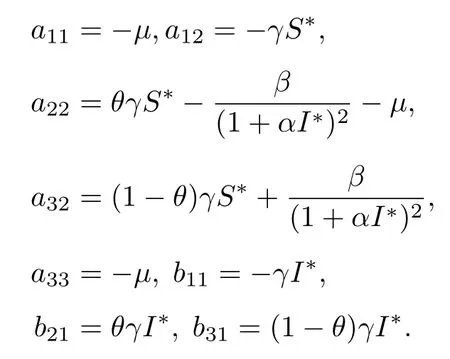
对于所满足的纽曼边界条件,易知Δ 有特征值-k2(k∈{0,1,2,···}),模型(2)的特征方程为

其中I是 3×3 的单位矩阵,且

将特征方程(4)展开,得到如下表达式:

其中

3.1 Turing 不稳定

本小节重点研究在无时滞的情形下,即τ=0时,扩散项对模型(2)稳定性的影响.

当无扩散,即d1=d2=d3=0 时,模型(2)在E*处的特征方程为

其中

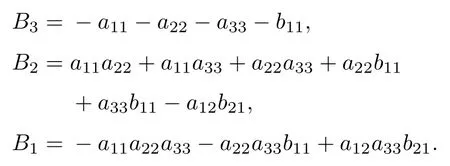
由Roth-Hurwitz 稳定判据可知,当假设

成立时,方程(6)所有的根都具有负实部.因此,模型(2)在平衡点E*处是局部渐近稳定的.

当扩散效应出现时,即di＞0(i=1,2,3) 时,模型(2)在E*处的特征方程为

其中

并且

定义

做如下假设:

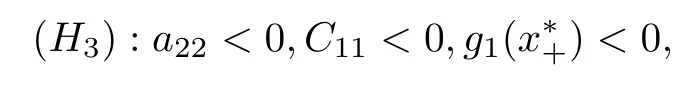
其中

引理1当B1＞0 和 (H3)成立时,方程g1(x)=0有两个正根x-和x+(0＜x-＜x+),使得当x∈(x-,x+)时,有g1(x)＜0 .

定理1假设R0＞1,τ=0,并且(H1)—(H4)成立.对于模型(2),以下结论成立 :

1) 当di=0(i=1,2,3) 时,模型(2)的谣言传播平衡点E*是局部渐近稳定的;

2) 当di＞0(i=1,2,3) 时,模型(2)在谣言传播平衡点E*处发生Turing 不稳定.

3.2 Hopf 分岔

本小节主要研究反应扩散谣言传播模型(2)的时滞诱导Hopf 分岔.

当τ=0,di＞0(i=1,2,3) 时,模型(2)的特征方程为(7)式.做出如下假设:

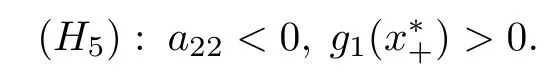
由(8)式可知,若B3＞0 成立,则有C3(k2)＞0 ;若B2＞0 和 (H5)成立,则有C2(k2)＞0;若B1＞0 和(H5)成立,对于任意的x＞0 ,都有g1(x)＞0,于是得C1(k2)＞0.

计算可得

其中

做出如下假设:

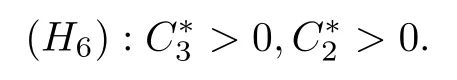
若B3B2-B1＞0 和 (H6)成立,则对任意k∈{0,1,2,3,···},有

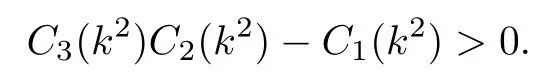
根据Routh-Hurwitz 稳定判据,若 (H2),(H5) 和(H6)均成立,对于任意的k∈{0,1,2,3,···},方程(7)的根均具有负实部.此时,无时滞模型(2)在谣言传播平衡点E*处是局部渐近稳定的.

当τ＞0,di＞0(i=1,2,3) 时,模型(2)的特征方程为(5)式.令λ=iω(ω＞0) 并代入(5)式,分离实虚部得到

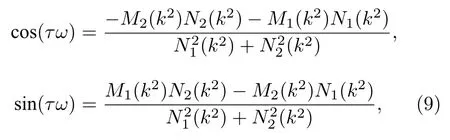
其中

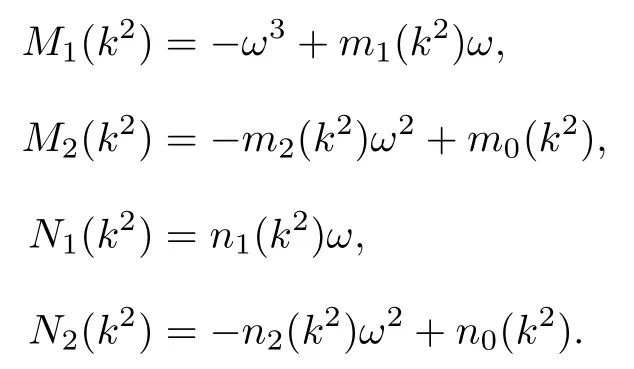
根据 cos2(τω)+sin2(τω)=1 可得

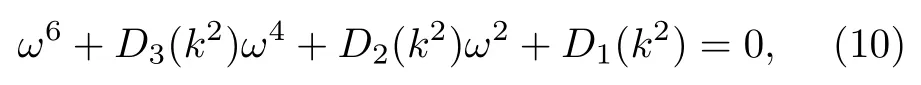
其中

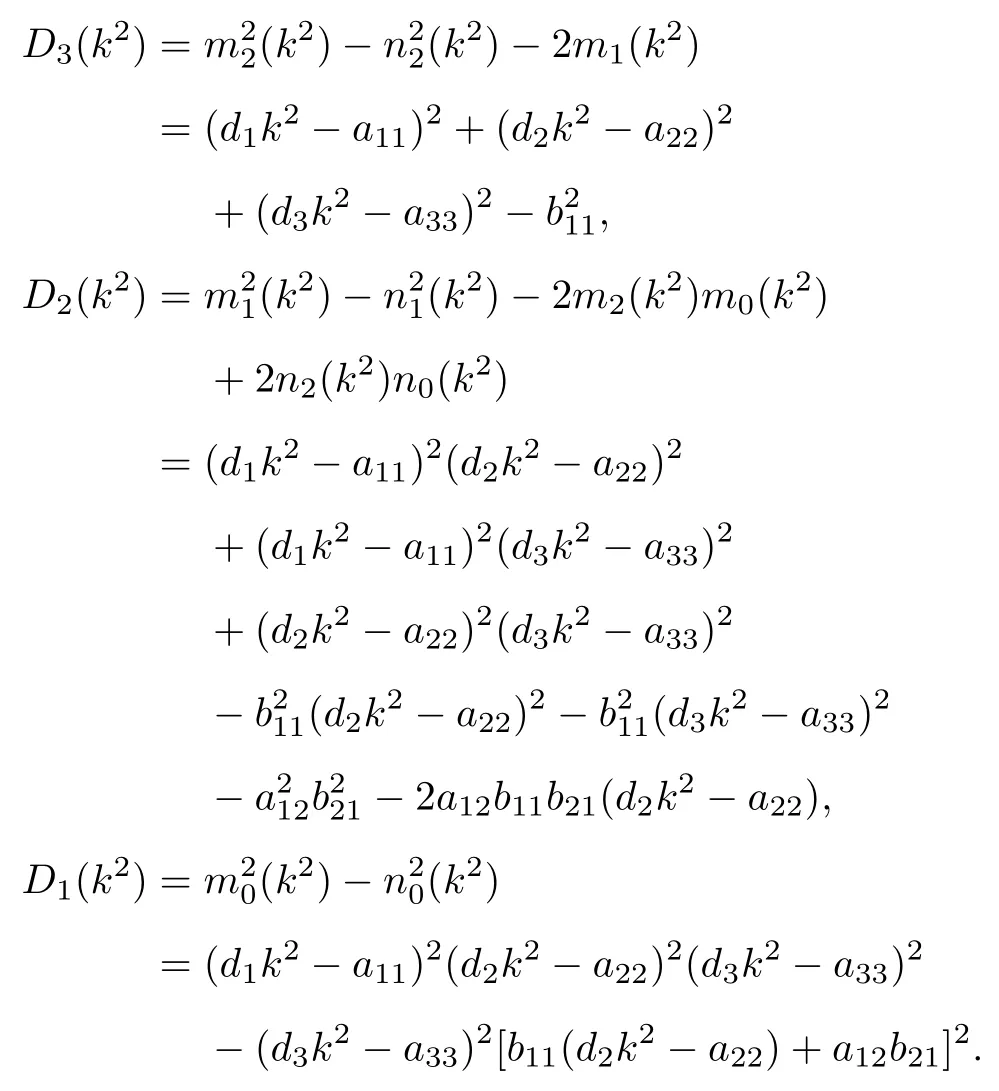
令z=ω2,则(10)式变为

令

当k=0 时,若以下条件成立:

则有g3(0)|k=0=D1(0)＜0,且=+∞,根据零点定理可知,此时方程g3(x)|k=0=0内至少存在一个正根.不失一般性,假设方程g3(x)|k=0=0 存在三个正根xn(n=1,2,3),则特征方程(5)|k=0存在三个纯虚根 iωn,其中ωn=(n=1,2,3).

由(9)式可得

其中

定义

当k≥1 时,令j=k2.定义

假设:

若 (H8)成立,那么当j≥1 时,Ei(j)(i=1,2,3) 是单调递增的,有

做如下假设:

若 (H9)成立,则有Di(k2)=Ei(j)≥Ei(1)＞0(i=1,2,3),于是有方程(11)|k≥1无正根.

验证k=0 时的穿越条件,对(5)式两边同时关于τ求导,于是有

其中

将τ=τ0和λ=iω0代入(14)式,得到

其中

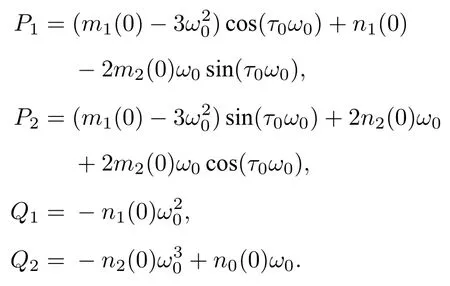
于是,

则,

做如下假设:

若满足 (H10) ,则.基于上述讨论,得到如下定理:

定理2假设R0＞1,di＞0(i=1,2,3),并且(H1),(H2),(H5)—(H10) 成立.对于反应扩散谣言传播模型(2),以下结论成立:

1) 当τ∈[0,τ0)时,谣言传播平衡点E*是局部渐近稳定的;

2) 当τ＞τ0时,谣言传播平衡点E*是不稳定的;且当τ穿越τ0时,模型(2)在E*附近发生Hopf分岔.

4 数值仿真

本节在文献[10]的基础上选取参数,通过数值计算与分析来验证上述理论的正确性,并研究谣言已知者I种群数量对辟谣信息传播的饱和作用.

选取模型(2)的参数为Λ=0.8,γ=0.6,µ=0.3,α=0.5,β=0.2,θ=0.7.此时假设 (H1) 成立.通过计算得R0=2.24＞1 以及谣言传播平衡点E*=(1.0595,0.7584,0.8487).

下面首先研究空间扩散对无时滞谣言传播模型稳定性的影响,此时τ=0.研究选取的初始条件为S(x,0)=1.0595+0.1cosx,I(x,0)=0.7584+0.1cosx,R(x,0)=0.8487+0.1 cosx.当d1=d2=d3=0 时,通过验证可以得到假设 (H2) 成立.由定理1 可知,模型(2)平衡点E*处是局部渐近稳定的,数值仿真结果如图1 所示;当d1=6,d2=0.01,d3=0.01 时,通过验证知假设 (H3) 和 (H4) 均成立.根据定理1,模型(2)在E*处失去其稳定性,发生Turing 不稳定,数值仿真结果如图2 所示.图3 是模型(2)发生Turing 不稳定时的Turing斑图.

图1 当 τ=0,d1=d2=d3=0 时,模型(2)在 E* 处是局部渐近稳定的Fig.1.Model (2) is locally asymptotically stable at E* when τ=0,d1=d2=d3=0.

图2 当 τ=0,d1=6,d2=0.01,d3=0.01 时,模型(2)在 E* 处是不稳定的Fig.2.Model (2) is unstable at E* when τ=0,d1=6,d2=0.01,d3=0.01.

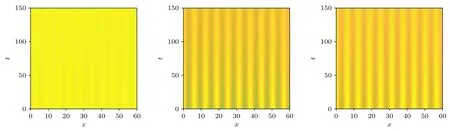
图3 Turing 不稳定发生时模型(2)的Turing 斑图Fig.3.Turing patterns of model (2) when Turing instability occurs.

从图1 可以看出,在无扩散时,随着时间的推移,社交网络中未知者S、已知者I和恢复者R这三类人群的密度分别快速收敛于1.0595,0.7584和0.8487,这说明谣言在人群中稳定持续地存在着.从图2 可以看出,引入扩散项后,谣言传播在空间上呈现周期振荡的趋势,这意味着谣言于短时间内大规模地在社交网络中快速地传播开来.

其次,验证由时滞诱发的Hopf 分岔.令d1=d2=d3=0.1,并选取初始条件为S(x,0)=1.25,I(x,0)=0.85,R(x,0)=0.74.计算可知此时ω0=0.5513,τ0=2.6332,通过验证可以得到假设(H5)—(H10)均成立.根据定理2,当τ=2.6＜τ0=2.6332时,模型(2)在E*处是局部渐近稳定的,仿真结果如图4 所示;当τ=2.655＞τ0=2.6332 时,模型(2)在E*处变得不稳定,仿真结果如图5 所示.

从图4 和图5 可以看出,当时滞τ小于分岔阈值τ0时,三种状态的网民密度趋于固定值,这表明此时人群中始终存在固定数量的谣言已知者;当时滞τ大于分岔阈值τ0时,三种状态的网民密度呈现出周期振荡,意味着谣言在社交网络中持续存在且周期性地传播,在增加谣言治理难度的同时也带来了新的风险.图6(a)是τ=2.6 时模型(2)在位置x=4 处的相图,图6(b)则是τ=2.655 时模型(2)在位置x=4 处的相图.

图5 当 τ=2.655＞τ0=2.6332 时模型(2)的波形图Fig.5.Waveform plots of model (2) with τ=2.655＞τ0=2.6332 .

图6 模型(2)在位置x=4 处的相图 (a) τ=2.6;(b)τ=2.655Fig.6.Phase diagram of model (2) at x=4: (a) τ=2.6;(b) τ=2.655.

最后,研究饱和因子α对模型(2)稳定性的影响.为方便讨论,取d1=d2=d3=0,其他参数不变,选取不同的α.从表1 可以看出,随着I种群数量的饱和因子α增大,对辟谣效果的抑制作用也增大,人群中谣言已知者I的密度变大,谣言未知者S和恢复者R的密度则减小,并且谣言在社交网络中发酵期时滞的分岔阈值τ0减小.

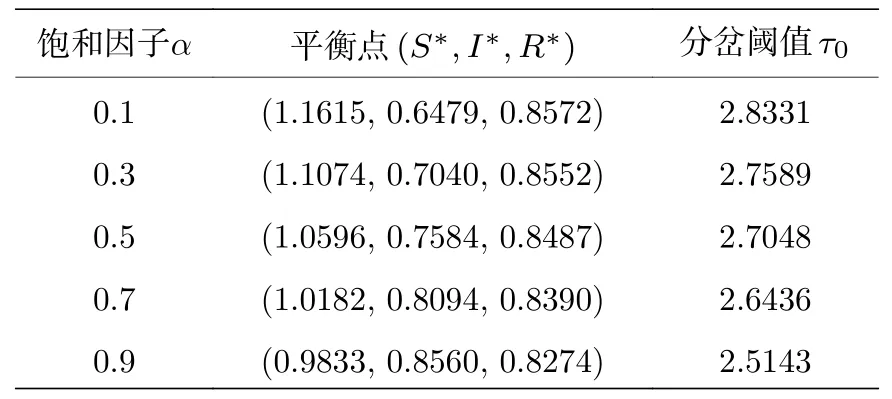
表1 不同α 对应的平衡点与分岔阈值Table 1.Equilibrium point and bifurcation threshold for different α.

图7 是τ=2.4 时谣言已知者I的密度在α不同取值情况下的波形图.显然,α的增大不仅会使得谣言在更大范围内传播,还会延长谣言从产生到趋于稳定的时间,并且带来更大的传播峰值.

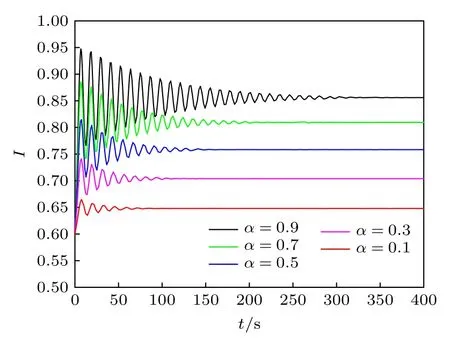
图7 不同α 取值时I 的波形图Fig.7.Waveform of I with different values of α.

5 结论

本文将发酵期时滞、空间扩散以及饱和辟谣函数引入到传统SIR 谣言传播模型中,研究了谣言在社交网络中传播的时空动态演化特性.首先,在稳定的无时滞谣言传播模型中引入扩散项,给出模型发生Turing 不稳定的条件,证明了Turing 不稳定正是由扩散诱导的.其次,选取发酵期时滞作为分岔参数,给出模型产生Hopf 分岔的条件及分岔阈值τ0的表达式.当τ＜τ0时,含有扩散项的谣言传播模型是稳定的;当τ＞τ0时,模型失去稳定性并发生Hopf 分岔.最后,在数值仿真部分验证了前文的结论,并且模拟了I种群数量的饱和因子α对于谣言传播的影响.α的增长表示I出现严重的拥挤现象,辟谣效果被削减,分岔阈值τ0减小,传播峰值增大.这些结论为谣言预防和治理提供了新的理论依据.因此,监管仍处于发酵期的谣言,提高辟谣信息发布的时效性,加大对特定人群的辟谣力度,是构建良好社交网络环境的重要内容.当前,本文主要研究的是时间滞后与空间扩散对社交网络中谣言传播的影响,在未来的工作中将进一步考虑多渠道对谣言传播的影响并继续研究分岔方向与分岔周期解的稳定性.