基于ADR-SDP-DCNN算法的非稳定工况下港口起重机轴承故障诊断
李胜永,吴丽华,戴雨
(1.江苏航运职业技术学院交通工程学院,江苏 南通 226010;2.江苏省交通运输厅规划研究中心,南京 210001)
0 引 言
港口起重机是港口机械的重要组成部分,因其具有频繁启停非稳定工况、服役期长及工作环境恶劣等特点,易发生传动机构故障,而在各类故障中,轴承故障尤为常见。因此,对港口起重机轴承进行在线监测及故障诊断,能够在一定程度上保障港口起重机健康可靠运行,有效避免因轴承故障而造成的经济损失及安全事故。
近些年来,关于轴承故障诊断的研究涌现出较多成果,形成了一系列经典的诊断方法,如变分模态分解、经验模态分解(empirical mode decomposition, EMD)、经验小波变换(empirical wavelet transform , EWT)、机器学习算法等。也有少数研究将上述方法应用到港口起重机的故障诊断中,如严华等将EMD方法用于港口起重机轴承故障的特征提取,钱志远将反向传播神经网络(back propagation neural network, BPNN)用于港口起重机的故障诊断与分类,沈科宇等使用支持向量机对港口起重机轴承故障进行诊断。但上述方法大多是针对稳定转速工况下的轴承故障诊断的,而港口起重机通常处于频繁启停这一非稳定转速工况下,对于这类非稳定工况,若直接应用上述方法将会得到不理想的诊断结果。这就需要提前将信号转化为相对稳定的信号,角域重采样(angular domain resampling, ADR)技术便能满足这一需求,如CHEN等和HOU等均将该技术用于解决非稳定信号的转化问题,再结合EMD或EWT等常见方法对轴承进行故障诊断。随着深度学习技术的快速发展,越来越多的研究将其应用于轴承故障诊断,如HOU等将不同故障轴承振动信号的峰度图作为深度卷积神经网络(deep convolutional neural network, DCNN)的输入进行训练与诊断,SINGH等将故障轴承声发射信号的声谱成像图作为DCNN的输入进行训练与诊断,均取得了比经典方法更高的诊断准确率。
针对上述所提到的港口起重机频繁启停这一非稳定工况而导致的轴承故障难以诊断的问题,本文将经典方法与深度学习技术相结合,创新性地提出一种基于ADR-SDP-DCNN算法的轴承故障智能诊断方法,这里SDP是对称点阵(symmetrized dot pattern)图像分析方法的简称。首先应用ADR技术将非稳定工况下采集的轴承振动信号转化为稳定信号,并借助自适应噪声完备集合经验模态分解(complete ensemble empirical mode decomposition with adaptive noise, CEEMDAN)对信号进行分解与重构的降噪处理,再通过SDP方法将重构信号进行图像化,最后应用DCNN对SDP图像进行训练与识别,发挥DCNN在图像识别与处理方面的优势,实现对港口起重机轴承故障的智能诊断。
1 ADR-SDP-DCNN算法
1.1 ADR及阶次分析
ADR技术的核心原理为:将通过传感器获取的非稳定工况下的原始信号,根据等角度间隔按照一定方式重新采样,获得相对稳定的信号,即角域信号。通过对角域信号进行傅里叶变换可得到阶次谱图。ADR技术具体实现过程如下:
假设参考轴在匀加速工况下工作,其转角可表示为
()=++
(1)
式中:、和为待定系数;为采样时间。
设Δ为键相脉冲对应的参考轴转角增量,Δ为定值,、、为3个连续键相脉冲到达时间,则有

(2)
将式(2)代入式(1),得到

(3)
通过式(3)计算、、,再代入式(1)可得到在[0,2Δ]范围内的任意转角在时域振动信号中对应的时间点:

(4)
为防止信号出现过采样现象,通常将转角的取值范围设置为
Δ2≤≤3Δ2
(5)
按照下式对的重采样进行离散化:
=Δ
(6)
式中:Δ为所期望的等角度间隔;为插值系数。将式(6)代入式(5),可得
Δ(2Δ)≤≤3Δ(2Δ)
(7)
综上,式(4)可转换为

(8)
通过式(8)可计算得到原始信号中的等角度间隔所对应的采样点时间,而采样点时间所对应的幅值通常利用三次样条或线性插值算法得到。
1.2 SDP方法原理
图1为SDP方法原理图,其中:()表示极坐标半径;()与()分别表示极坐标以逆时针和顺时针方向沿初始线旋转的角度;为角度放大因子。
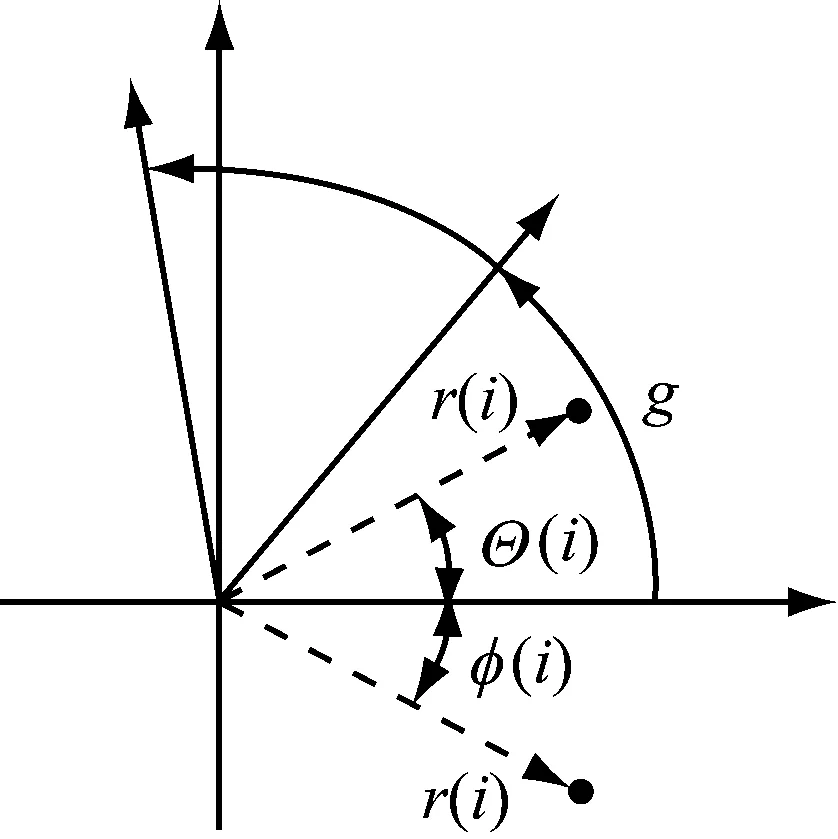
图1 SDP方法原理图
对于所采集的某一原始信号,设其时刻和+时刻所对应的幅值分别为和+,其中为时间间隔参数,则利用式(9)~(11)将该信号转化为极坐标空间((),(),())中的点。
()=(-)(-)
(9)
()=+(+-)(-)
(10)
()=-(+-)(-)
(11)
式中:和分别表示原始信号幅值的最大值和最小值。由式(9)~(11)可知,参数、、直接决定原始信号在极坐标空间((),(),())中的位置,通过理论分析及试验表明,在0<≤10,=60°,<时,能够最大化体现不同信号的差异性。
1.3 DCNN
DCNN因其具有自主学习、逐层提取特征的性质,能够实现图像端到端分类,从而能够有效避免因人工提取特征不合适而造成分类结果不理想的情况。通常一个典型的DCNN结构包括1个输入层、多个卷积层和池化层、1个或多个全连接层和1个输出层,见图2。
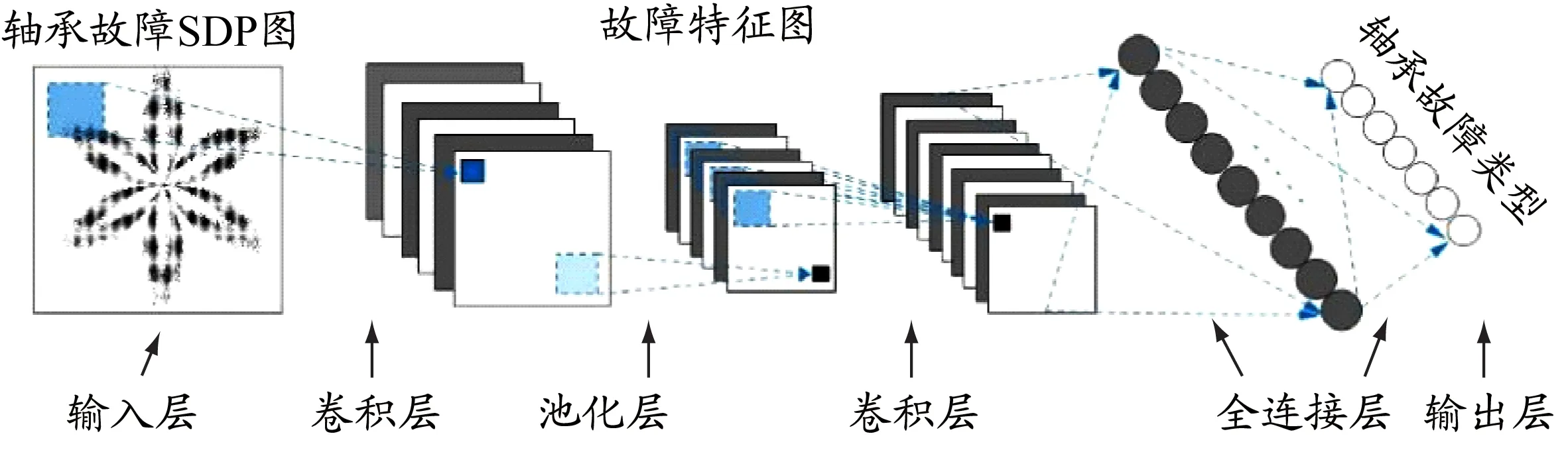
图2 典型的DCNN结构
各层的基本原理和作用如下:
输入层:包括图像及文本等数据的输入,在输入前,通常还需对输入对象进行预处理,如统一图像大小、进行归一化处理等。在本文研究中,输入对象为SDP图。
卷积层:该层是DCNN的核心部分,该层具有多个卷积核且同时具有权值共享的优点,使其模型参数个数能够大大减少,从而简化模型。卷积原理如式(12)所示。
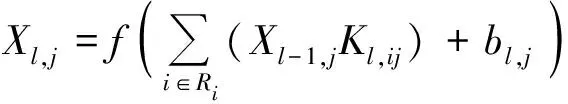
(12)
式中:,、-1,分别为当前层、上一层-1的第个输出特征图;(·)为激活函数;为输入特征图集;,和,分别为卷积核和偏置。
池化层:该层是对输入数据进行下采样,也称为下采样层。具体原理如式(13)所示。
,=down(-1,)
(13)
式中,down(·)为下采样函数,即所选择的池化方法,常用方法包括最大池化、均值池化等。
全连接层:该层主要对前一层的输出进行全局分析处理,整合具有区分性的局部信息,并进行非线性组合。具体原理如式(14)所示。
,=(,-1,+,)
(14)
式中:(·)为激活函数;,为权值。
输出层:该层将全连接层的输出进行分类,通常采用Softmax分类器。
DCNN使用误差反向传播算法训练网络,得到优化参数,、,、,等。本文中,DCNN所采用的损失函数为均方误差:

(15)

2 基于ADR-SDP-DCNN算法的港口起重机轴承故障诊断步骤
基于ADR-SDP-DCNN算法的港口起重机轴承故障诊断具体步骤如下:
搭建港口起重机轴承故障试验台进行试验,采集轴承的原始振动信号()。
将原始振动信号()进行ADR处理,其中插值方法选择三次样条插值算法,经过ADR处理后得到角域振动信号()。
应用CEEMDAN对信号()进行分解,得到一系列固有模态分量:

(16)
式中:()为()的第个固有模态分量;()为余项。选取前6个高频分量进行信号重构时去噪效果最佳,基于此,得到重构信号
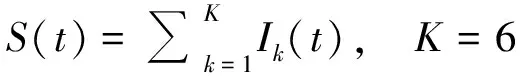
(17)
对每个样本均执行步骤3,得到信号样本集,并随机抽取样本进行步骤5的SDP参数确定。滚动轴承的故障特征频率计算方式如下:

式中:、、、分别为滚动轴承的转动频率、外圈故障特征频率、内圈故障特征频率、滚动体故障特征频率;为滚动轴承固定转速;为滚动体直径;为轴承节径;为滚动体个数;为接触角。滚动轴承的故障阶次为
=,=o,i,b
(22)
采用皮尔逊相关系数法确定SDP参数,具体方式如下:
①从步骤4得到的样本集中,随机抽取每个故障类型的样本及无故障样本各10个。根据SDP方法理论可得,=60°,<,0<≤10。为得到最优的(,)组合,以5°为步长遍历取值区间[20°,50°],以1为步长遍历取值区间[1,5],对(,)的全部组合计算SDP图。这里取值区间选取依据见下文中参数、、对SDP图的影响分析。
②为降低样本偶然性对参数选取的影响,将相同参数下同一类故障SDP图的二维矩阵数值进行叠加处理,重构一个代表性样本。
③采用皮尔逊相关系数法分析某一组合下任意两个SDP图的相关性,计算两个图之间的相关系数:
(,,)(,)=

(23)

④定义并计算不相关度(,,):
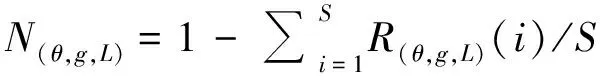
(24)
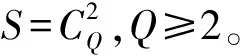
随后,跟着台达的步伐,媒体记者走进了由武汉众维亿方大数据科技有限公司打造的武汉临空港数据基地,临空港数据基地一期项目从2018年6月起正式实施。在一期项目中,已部署10个微模块机房,约2318个机柜,全部完成只花费了不到6个月的时间。该数据基地的运维总经理及设计总工表示,临空港数据基地建成后将成为华中区最大的互联网数据中心,可以满足临空港乃至武汉市、华中区最严苛的网络数据服务要求。
根据步骤5得到的参数值、、,对步骤4中的全部样本进行SDP图生成,并将生成的SDP图样本集根据合适的比例分成DCNN训练样本集和测试样本集。
根据试验样本特点,确定DCNN结构,并将训练样本集中的SDP图输入DCNN进行训练,得到已训练好的DCNN模型。
将测试样本集中的SDP图输入训练好的DCNN模型中进行测试,计算诊断准确率并完成港口起重机的故障诊断。
3 试验研究
3.1 试验方案及数据预处理与阶次分析
为验证所提方法有效性,根据港口起重机轴承工况特点搭建如图3(左图)所示港口起重机轴承故障试验台。该试验台包括控制柜、电机、带传动机构、轴承座、联轴器、负载装置和加速度传感器,采用6205型深沟球轴承代替港口起重机轴承进行试验,并将轴承的轻微裂纹和轻微点蚀作为本文所研究的故障类型。具体故障植入位置如图3(右图)所示。

图3 港口起重机轴承故障试验台(左图)及轴承故障植入位置(右图)
变转速这一非稳定工况通常可近似为匀变速工况,这里采取转速从0到1 500 r/min均匀加速工况,加速时间为12.8 s。为确保训练DCNN时具有足够的样本,对6个不同故障轴承(故障类型分别为内圈裂纹、内圈点蚀、外圈裂纹、外圈点蚀、滚动体裂纹、滚动体点蚀)和1个正常轴承均进行匀加速工况下的150次重复试验,得到1 050个原始时域振动信号。分别选取这7个轴承第1次试验时得到的信号,截取前7 000个采样点绘制原始时域振动信号波形图,见图4。

图4 轴承原始时域振动信号波形
经过ADR处理后,得到角域振动信号。图5为内圈有裂纹的轴承时域振动信号与角域振动信号的对比。图5显示,角域振动信号的故障周期间隔相等,采样点分布均匀,仅幅值随着角度增加而增大,但逐渐趋于平稳。为进一步比较ADR处理前后信号的差别,计算其时域振动信号的频谱图和角域振动信号的阶次谱图(见图6),并根据式(18)~(22)计算轴承内圈部位的故障阶次,见表1。

表1 轴承内圈故障阶次

a)时域振动信号
分析图6a可知,非稳定工况下时域振动信号经快速傅里叶变换后得到的频谱图存在较为严重的频率混叠现象,基本无法进行故障诊断;分析图6b角域振动信号阶次谱图可以发现,4阶和5阶的谱线较为明显,表明该轴承内圈存在故障,其阶次计算值分别为21.27和26.57,与理论值21.6和27存在些微误差,这是因为ADR技术中利用三次样条插值算法计算幅值,计算值与理论值存在误差。

a)时域振动信号的频谱图
利用CEEMDAN对该角域振动信号进行去噪处理与信号重构,得到15个固有模态分量。高频固有模态分量通常包含大部分故障信息,故本文选取前6个高频固有模态分量进行信号重构。为验证CEEMDAN的去噪作用,对重构信号重新进行阶次分析,得到的阶次谱图见图7。
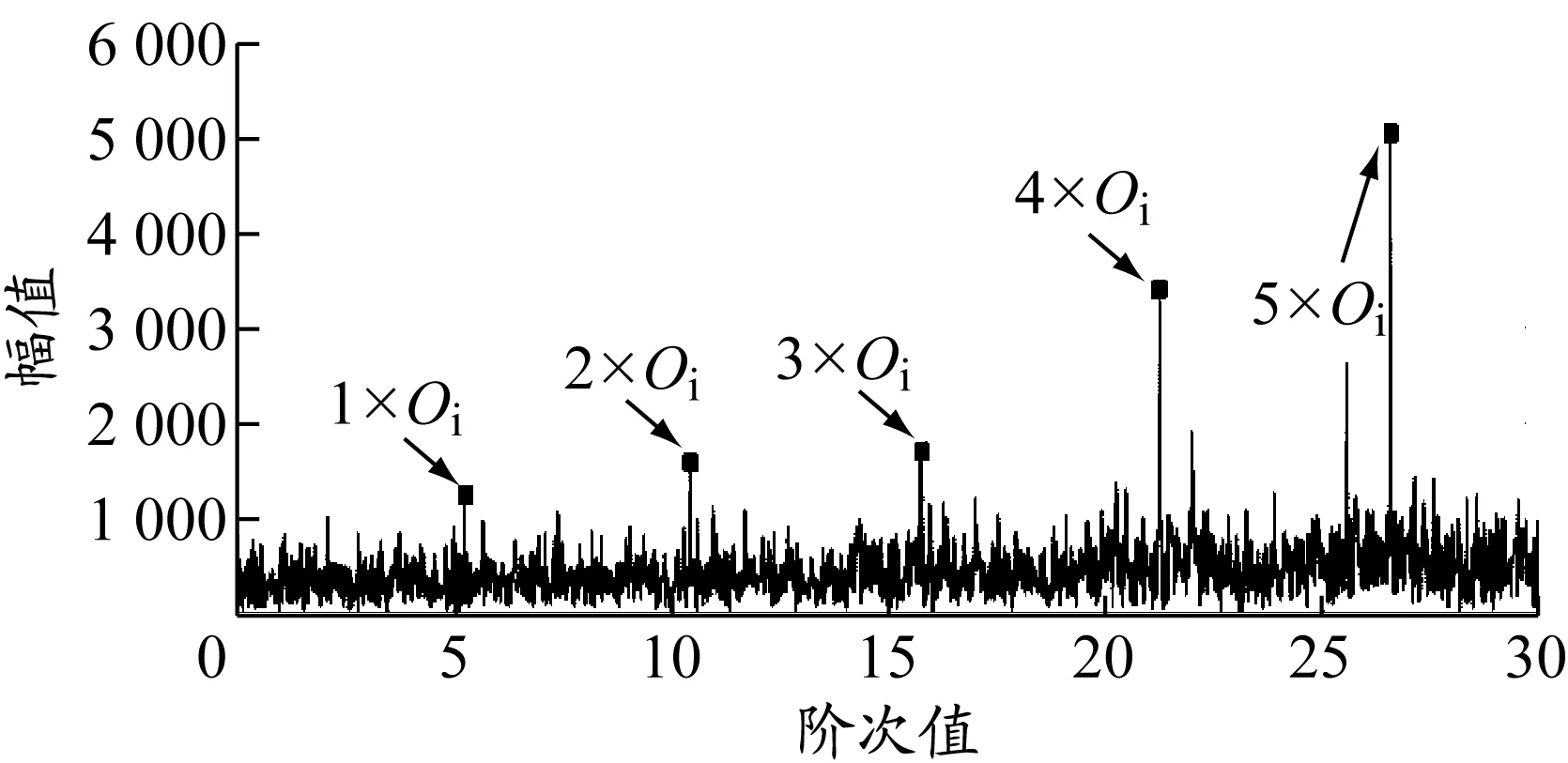
图7 经CEEMDAN去噪重构后信号的阶次谱图
对比图7与图6知,经CEEMDAN去噪重构处理后,4阶和5阶的谱线更为明显,且1阶至3阶的谱线也易于发现,表明CEEMDAN能够有效降噪。通过频谱和阶次谱分析可知,传统故障诊断方法存在两点不足:一是需要专业技术人员进行相关计算及图像分析;二是通过频谱图或阶次谱图仅能判断出轴承故障发生部位,无法判断故障类型。因此,下文采取SDP方法和DCNN对故障轴承进行智能诊断,以弥补传统方法存在的不足。
3.2 基于皮尔逊相关系数法的SDP参数选取
首先根据本文案例分析参数、、对SDP图的影响,为参数的选取提供依据。以上文中重构的角域振动信号样本为例,令=60°,分别取1、5、10,分别取20°、40°、60°,作SDP图,见图8。分析图8可知:参数主要影响图案臂沿初始线旋转的角度,越大,旋转角度越大,图案臂的厚度也有所增加;参数主要影响图案臂的曲率,越大,图案臂曲率则越小,图案臂的厚度也会有所增加。

图8 参数L、g对SDP图像的影响(θ=60°)
综上可知,SDP图的差异性主要体现在图案臂沿初始线旋转的角度、图案臂厚度和图案臂的曲率大小上。因此,选取的取值区间为[20°, 50°]、步长为5°,选取的取值区间为[1, 5]、步长为1,进行不同(,)组合下不相关度(,,)的计算。为直观地体现(,,)与、的关系,绘制折线图,见图9。分析图9可知,当=30°,=1时,具有最大值;在=30°左侧,不相关度大体上呈递增趋势,而在=30°右侧,不相关度则呈递减趋势:故可直接确定的值为1,的值为30°。参数确定后,计算得到7个代表性样本间相关系数矩阵,见表2。选用同一类故障中的10次试验数据,进行各故障类型样本的平均自相关系数计算,结果见表3。

图9 不相关度与SDP参数关系
由表2可知,最大相关系数为0.752 4,最小相关系数为0.609 7,相关系数平均值为0.672 2;分析表3可知,平均自相关系数最小值高于0.752 4,且均值也远高于0.672 2:这说明不同故障类型的SDP图具有一定的差异性,验证了利用SDP图进行故障诊断的可行性。

表2 参数L=1,g=30°下的7个代表性样本相关系数矩阵

表3 参数L=1,g=30°下各故障类型样本的平均自相关系数
3.3 DCNN构建与轴承故障诊断
本文研究的样本共有7种类型,各类型样本分别包括100个SDP图训练样本和50个的SDP图测试样本,每个SDP图尺寸为656×656。根据上述样本实际情况和模型构建经验,确定DCNN的结构如表4所示,训练批量大小为20,算法学习率为0.15,算法共迭代150次,池化方法选择最大池化法。

表4 DCNN结构
将7种类型共计700个SDP图训练样本输入上述DCNN,对模型进行训练,同时将350个SDP图测试样本输入模型进行测试。算法每迭代一次,就对测试样本进行一次测试,并计算诊断准确率。每次迭代对应的训练样本和测试样本的诊断准确率见图10。迭代到第150次时,对训练样本和测试样本的诊断结果见图11。

图10 训练样本和测试样本诊断准确率
由图10可以发现,在整个训练周期内,训练样本和测试样本的诊断准确率均随着算法迭代次数的增加而增加,在迭代到第150次时,训练样本诊断准确率达97.14%,测试样本诊断准确率达96.00%;测试样本的诊断准确率均略小于训练样本的诊断准确率:这均体现出DCNN结构设置得较为合理,模型参数训练得较好,未出现过拟合现象。分析图11可以发现,无论是训练样本还是测试样本,模型对外圈裂纹的识别率均最低,均易于把外圈裂纹识别为无故障或其他故障类型,而模型对外圈点蚀的识别率在测试样本和训练样本中均达到了100%;从表3也可以发现,外圈点蚀的自相关系数最高,外圈裂纹的自相关系数则较低:故出现此类结果,这也与在上述对SDP图相关度分析时的结论较为吻合。

a)训练样本
3.4 不同诊断方法对比
为进一步验证本文所提方法在多种非稳定工况下的有效性和先进性,再设置5种方案分别对3种非稳定工况(匀加速、匀加速-匀速-匀减速、匀加速-匀减速-匀加速工况)进行试验对比研究,其中方案A、B为自设方案,方案C、D、E为现有文献中的方案,具体如下:
方案A:将未经ADR和CEEMDAN处理的时域振动信号作其SDP图输入DCNN。方案B:将经ADR处理但未经CEEMDAN处理的角域振动信号作其SDP图输入DCNN。方案C:将未经处理的时域振动信号经文献[21]所提算法处理后输入BPNN。方案D:将未经处理的时域振动信号经文献[22]所提算法处理后输入卷积神经网络(convolutional neural network, CNN)。方案E:将未经处理的时域振动信号经文献[23]所提算法处理后输入CNN。
为确保训练DCNN时有足够的样本,在每种非稳定工况下,将这7个代表性轴承均进行相同工况下的150组重复试验,即样本数量为1 050。将每个工况下所获取的样本按照上述5种方案分别进行诊断。
(1)匀加速工况。匀加速工况即为第3.1节中的试验工况:转速从0到1 500 r/min均匀加速,加速时间为12.8 s。诊断结果见图12。

图12 匀加速工况下的诊断结果对比
对方案A、方案B和本文方法进行比较发现,未经ADR处理时,由于时域振动信号是非稳定信号,其SDP图特征较为混乱,故仅有48.57%的诊断准确率,而经ADR处理后即达到93.71%的诊断准确率,但再经CEEMDAN去噪重构后诊断准确率则提高至96.00%,体现出本文所提方法的有效性。方案C、D、E的诊断准确率均低于本文所提方法:方案C也利用CEEMDAN进行了去噪重构,但其信号特征为手动提取的奇异值分解值,且分类器为BPNN,故仅能达到84.86%的诊断准确率;方案D的诊断准确率仅为33.71%,表明该方法无法处理非稳定信号;方案E的诊断准确率也仅能达到80.28%。
(2)匀加速-匀速-匀减速工况。试验前4 s转速从0到600 r/min均匀加速,中间4 s转速保持600 r/min不变,后4 s转速从600 r/min到0均匀减速。诊断结果见图13。

图13 匀加速-匀速-匀减速工况下的诊断结果对比
对方案A、方案B和本文方法进行比较发现,在匀加速-匀速-匀减速工况下,未经ADR处理的方案A基本无效,而经ADR处理后即达到92.86%的诊断准确率,再经CEEMDAN去噪重构后诊断准确率则提高到96.29%。方案C、D、E的诊断准确率均低于本文所提方法,与匀加速工况相比,方案C的诊断准确率有所降低,仅能达到77.42%;方案D基本无效;方案E较为稳定,诊断准确率能达到82.57%。
(3)匀加速-匀减速-匀加速工况。试验前4 s转速从0到600 r/min均匀加速,中间4 s转速从600 r/min到0均匀减速,后4 s转速从0到600 r/min均匀加速。诊断结果见图14。
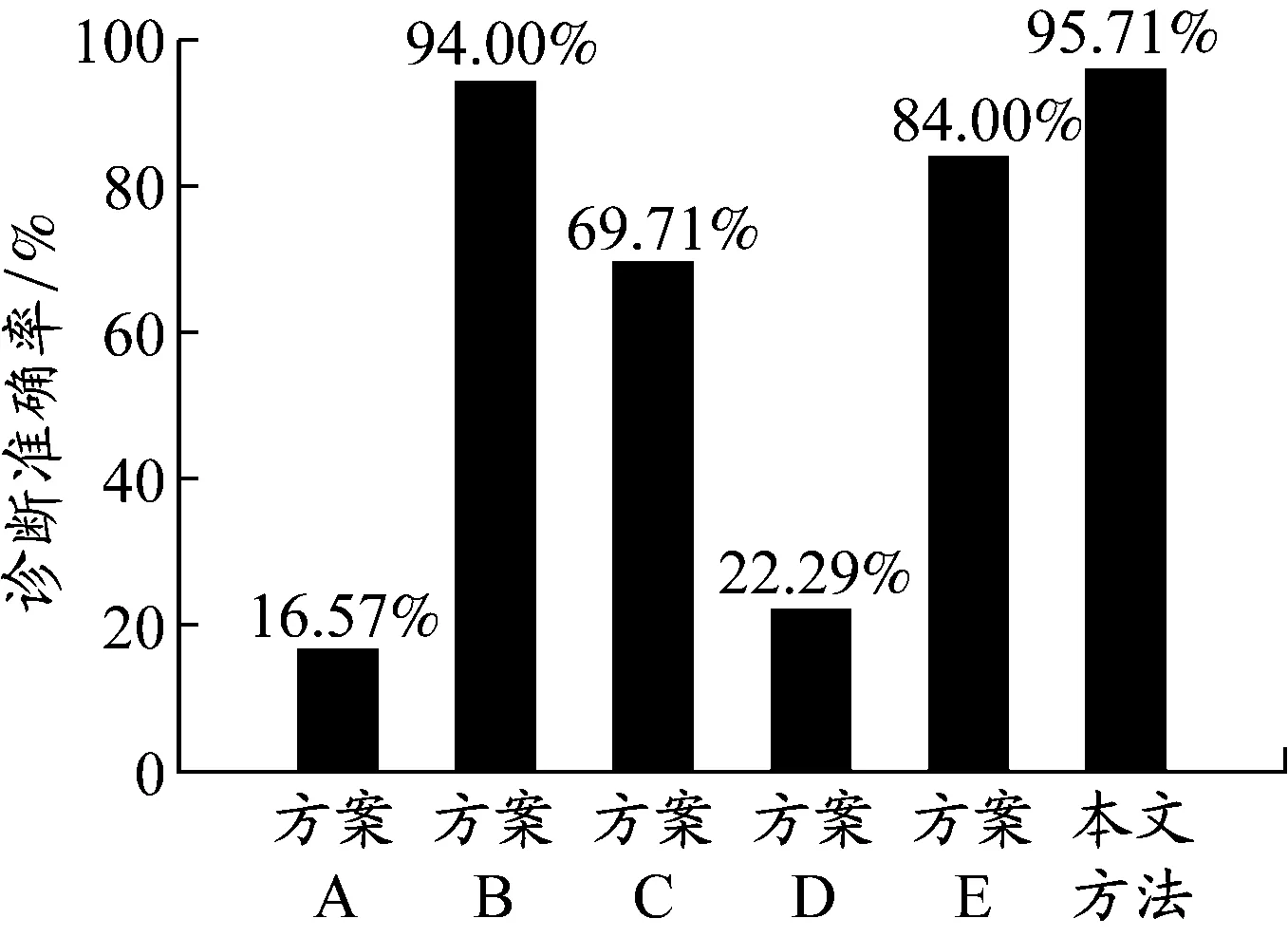
图14 匀加速-匀减速-匀加速工况下的诊断结果对比
对方案A、方案B和本文方法进行比较发现,在匀加速-匀减速-匀加速工况下,方案A同样基本无效,而经ADR处理后即达到94.00%的诊断准确率,但再经CEEMDAN去噪重构后诊断准确率则提高至95.71%。方案C、D、E的诊断准确率均低于本文所提方法,方案C的诊断准确率再次降至69.71%;方案D同样基本无效;方案E的诊断准确率则略微提高至84.00%。
综上可得:在非稳定工况下,SDP方法和DCNN分类器需要结合ADR技术才能得到较高的诊断准确率,再经过CEEMDAN处理后则可进一步提高诊断效果;对于多种非稳定工况,本文方法鲁棒性都较强,均能得到较好的结果,优于现有的数种常用方法,体现出所提方法的有效性和先进性。
4 结 论
针对港口起重机起升机构及运行机构中减速器频繁启停这一非稳定工况而导致的轴承故障难以诊断的问题,本文利用传统方法的优势,并结合深度学习技术,提出一种基于ADR-SDP-DCNN算法的港口起重机轴承故障智能诊断方法。通过试验研究,主要得到以下结论。
(1)ADR技术能够有效将非稳定的时域振动信号转化为相对稳定的角域振动信号,结合CEEMDAN进行去噪重构后能够有效剔除角域振动信号的噪声,保留主要的故障信息。(2)采用皮尔逊相关系数法能够有效筛选出适合本研究试验算例的SDP参数:当时间间隔=1、放大角度因子=30°、转角=60°时,7种不同故障的SDP图差异性最大。(3)本文研究发挥出DCNN在图像识别中的优势,在匀加速、匀加速-匀速-匀减速、匀加速-匀减速-匀加速3种工况下进行了港口起重机轴承非稳定工况模拟试验,本文所提方法分别达到了96.00%、96.29%和95.71%的诊断准确率,优于现有的数种常用方法,体现出本文所提方法的有效性和先进性。

