基流分割对城市雨洪模拟不确定性分析的影响

王京晶，徐宗学，赵 刚，李 鹏，叶陈雷，宋苏林

(1.北京师范大学水科学研究院，北京 100875；2.城市水循环与海绵城市技术北京市重点实验室，北京 100875；3.布里斯托大学地理科学学院，英国 布里斯托 BS8 1TH；4.济南市水文局，山东 济南 250014)

随着城市化的快速推进，由暴雨引起的城市洪涝灾害问题日益突出[1-2]。城市化进程的不断加快使得城市地表硬质化率越来越高、汇流时间缩短、洪水峰高量大；而随着城市建筑群的扩张，暴雨云团在城市区域面临的阻碍作用更加明显，云团的移动更加滞后缓慢，短历时强降雨现象愈加频发，上述种种变化也使得城市区域在遭遇暴雨时更加脆弱[3-5]。因此，如何精确模拟城市雨洪过程并做出精准预警预报对政府相关部门防灾减灾决策至关重要。

水文过程是一个受多因素(气象、下垫面特征、地形、人类活动)影响的复杂系统过程，而水文模型是人们通过一系列数理方程描述概化这一过程的工具，由于人为主观构建模型及对水文过程机理客观认识不足使得模型存在较强的不确定性，进而影响模拟精度[3,6-7]。城市雨洪模型是众多水文模型中的一个重要分支，它能模拟城市雨洪过程并进行预警预报[7]。城市雨洪模型的发展经历了经验性模型、概念性模型、物理性模型等3个阶段，比较著名的模型有SWMM(storm water management model)、InfoWorks、MIKE系列等模型，其中SWMM模型相较于其他模型具有开源免费、易操作等优点，成为应用最为广泛的城市雨洪模型之一[7-8]。

参数优化是模型模拟中的一个重要环节，传统参数优化方法基本思想是认为构建的模型只有一组最优参数组合。由于参数优化思想本身的缺陷，应用最优参数组合进行模拟预测很难保证模型应用效果与预测结果的可信度[9]。不确定性分析方法的发展提升了人们对参数优化体系的认知高度，其认为通过统计学手段优选提取的各参数组合的模拟结果均具有良好的可信度，避免了单一参数组合带来的洪水预警预报风险[9-10]。GLUE(generalized likelihood uncertainty estimation)方法是应用较为广泛的水文模型参数不确定性分析方法，可生成模型参数的后验分布范围，并通过设置一定的似然度进而输出模型结果不确定性范围[10-11]。目前不确定性分析的相关研究主要聚焦于对降水输入、模型参数误差等因素的分析，而从模型校验数据的角度探究数据误差对水文预报及模拟结果的不确定性分析的相关案例较少[12]。流量序列因其良好的长序列连续监测获取等特点，成为现阶段最常见的水文模型校验数据依据[9,12]。流量序列是影响水文模型模拟效果的重要因素之一，选择合适可靠的流量序列作为模型校验数据至关重要。尽管目前在水文模拟中，大多数理论默认实测流量数据是真实有效的，可直接用于模型率定，但根据刘松等[12]的研究，流量数据因流域水文要素异质性及监测水平等因素限制，可能存在较大的误差与不确定性。济南市主城区流域由于其特殊的地形地貌和地质构造，降水引发的山洪极易由南向北宣泄至城区形成内涝，且流域内地下水极易出露地表形成泉水进入河道，成为河道基流的重要组分来源[13]；流域出口断面洪峰流量中基流占比一般可达10%以上，此时基流的存在可能对直接使用流量序列校验模型的可靠性产生较大影响，不可忽视。因此，在模拟城市雨洪过程时，考虑校验数据即实测流量序列误差对模拟结果的影响尤为重要。

本文选择典型高度城镇化的济南市主城区流域为研究对象构建SWMM模型，应用GLUE方法探讨基流分割前后流量序列校验模型对模拟结果不确定性的影响，以期为济南市主城区流域洪水预报与制定防洪减灾方案提供参考。

1 研究区概况与研究数据

济南市位于山东省中西部，主城区流域涵盖济南市大部分城区(36°33′N～36°45′N，116°47′E～117°7′E)，流域面积约320 km2。流域雨热同期，降水具有明显的季节性特征，7—8月的降水可达到全年降水量的一半以上，多年平均降水量约为 650 mm[14-16]；流域降水时空变化较大，且流域地形南高北低，整体坡度大，排涝主要依靠设计标准较低与排涝能力有限的城区老旧排水系统，在应对短历时强降雨事件时极易形成“南洪北涝”“马路行洪”等现象[13-14]。流域内设有5座雨量站，且唯一出口断面设有黄台桥水文站。流域水系成羽系状，隶属于小清河水系，小清河是流域唯一排水通道，肩负防洪排涝重任[13-14]。流域大部分区域位于济南城市水系地下水排泄区，地表地下水交换复杂频繁，南部山区的地下水下泄至北部的城区遇透水性弱的挡水隔板阻碍极易出露地表成为泉水，形成百泉争涌的独特景观现象并最终排放至河道，因此济南别称“泉城”[13]。济南主城区流域水系及站点见图1。

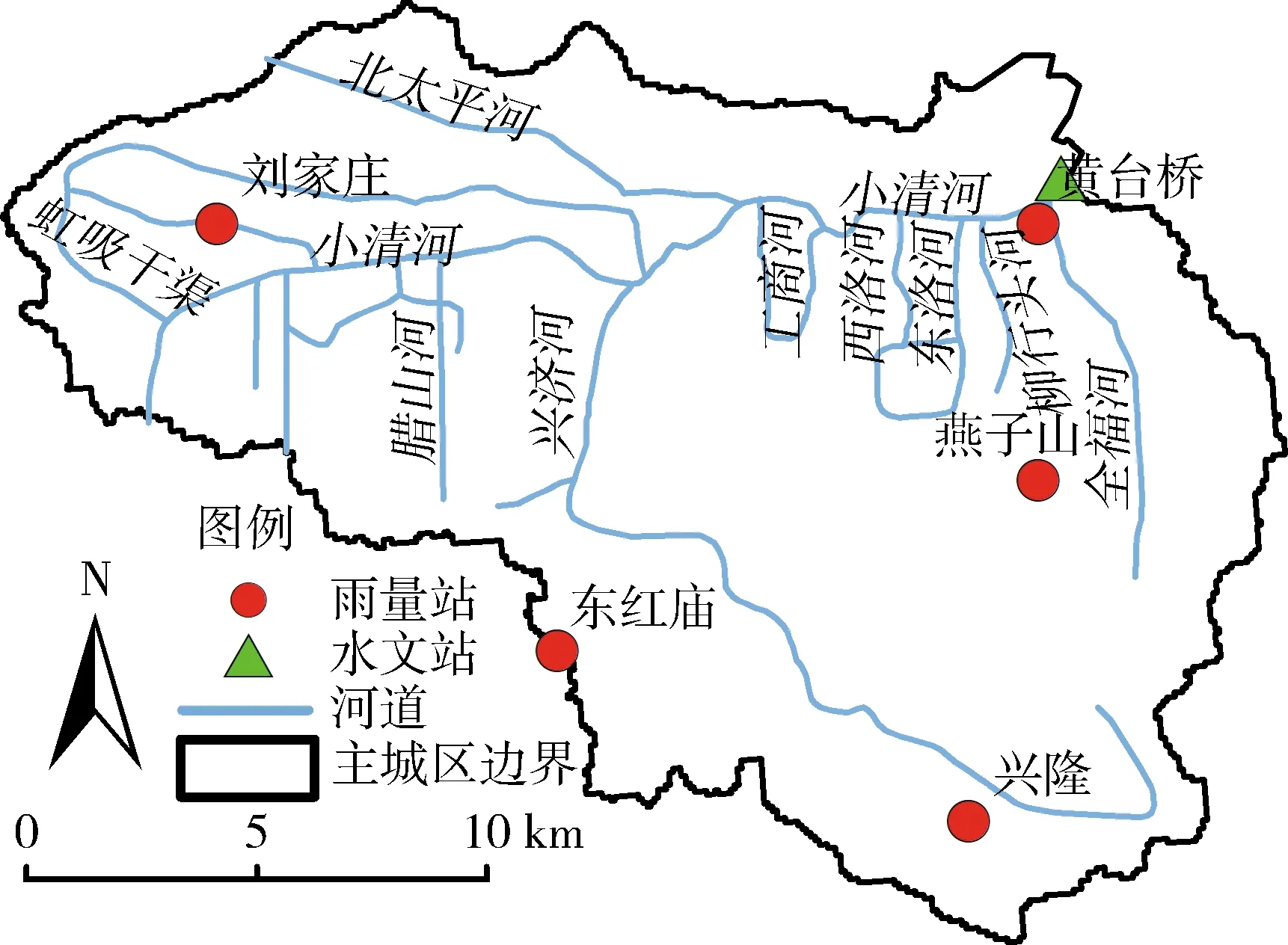
图1 济南主城区流域概况

考虑到2010年以后城市下垫面变化剧烈，水文资料一致性较差，为便于分析，假设2005—2010年下垫面未发生变化，并选取其中7场暴雨洪水资料用于模型率定与验证。选择东红庙、黄台桥、兴隆、燕子山、刘家庄等5座雨量站的降水数据通过泰森多边形雨量分配计算后用作模型输入数据，流域出口黄台桥水文站的流量序列作为模型校验数据；其中，20050730、20050915、20060803与20070809等4场洪水数据用于模型率定，20080717、20090616与20100819等3场洪水数据用于模型验证。部分河道、管网资料由济南市水文局提供。

2 研究方法

2.1 SWMM模型

SWMM模型是由美国环保署开发的城市雨洪模型，主要用于模拟城市雨洪过程[14,17-18]，目前最新版本为2020年7月20日更新的SWMM 5.1.015版。模型可动态模拟城市雨洪过程中场次或长时间序列的水文/水质过程，其计算过程主要分为地表产流、地表汇流、河道/管网汇流3部分[17,19]。本文选用适用于城镇化程度较高区域的Horton法计算地表产流；模型应用非线性水库法，联立曼宁方程和连续性方程来求解地表汇流；河道/管网汇流计算主要通过求解圣维南方程组实现，本文采用应用较为广泛且稳定性较强的运动波法进行计算[17,19]。经概化后，模型由100个河道和排水管网控制的子汇水区构建而成，涵盖1 800个排水节点。

SWMM模型参数众多，依据现有资料直接确定部分参数取值，对于不能直接确定的参数值，通过参考相关文献及SWMM模型用户手册确定其取值范围，再通过模型参数优化进行调整[14-15,17,19]。

2.2 GLUE方法

GLUE方法是一种应用较为广泛的水文模型参数不确定性估计方法，其核心思想是认为不同参数组合在同一评价指标约束下可达到相同模拟效果，即不认为只有唯一一组模型参数能够使模型模拟达到最优效果[9-11,20]；并认为达到一定似然度的参数组合的模拟结果都是有效的，且精度评价指标越高或越低(高或低由似然函数而定)，似然度越大，其置信度也就越高[12,20-21]。

GLUE方法计算的主要步骤如下：①确定模型参数范围及先验分布形式，通过随机采样方式抽取一定数量参数组合代入模型中运算得到模拟结果；②定义似然函数，计算模拟值与实测值的拟合程度，即似然度；③设置似然度阈值，筛选出有效参数组合，高于阈值的参数组合视为无效，似然值权重赋值为0，对低于阈值的参数组合似然值则进行归一化处理，即可得到似然函数或参数空间分布概率密度；④依据似然值大小排序，估算一定置信区间的不确定性范围，一般取累积概率密度分布图的5%和95%置信区间作为洪水预报不确定性范围的上下界限，得到参数后验分布，并进行不确定性分析[10,22-23]。

相比于传统水文预报不确定性分析的经典贝叶斯方法如SCEM-UA、MCMC方法，GLUE方法的表现则更加灵活，可主观选择似然函数与似然度阈值量化模型不确定性，具有较强的适用性[22,24]。

2.3 评价指标

似然函数的选择在不确定性分析中至关重要，它是用来筛选参数组合优劣集并评估模型模拟效果的重要参考[11,20]。本文选用均方根误差(RMSE)作为模拟效果评价指标。

根据相关文献[12,25-26]，选取区间覆盖率CR、区间平均宽度RB、平均偏移幅度D和平均对称度S这4个指标来评价模拟结果不确定性区间的优良性，计算公式为

(1)

(2)

(3)

(4)

式中：m为落在置信区间内的实测流量数据点数；n为实测流量数据点总数；Qi0、Qi1、Qi2分别为第i个流量实测值和模拟流量置信区间上下边界值，m3/s。

通常认为，在同样置信水平下，实测值区间覆盖率CR越高，越接近于100%，表明模拟值越接近实测值，模拟效果也就越好。区间平均宽度RB越小，预报区间的不确定性也就越小。平均偏移幅度D和平均对称度S是衡量预报区间对称度的指标，D和S越小，说明预测区间的偏移幅度越小，对称性越好，模拟效果可靠性就越高。

2.4 基流分割方法

基流一般是指河道中来源于地下水的延迟补给径流，是枯水期河道径流的主要组分[27-28]。泉水是济南市区河道的“活水”之源，对整个济南城市水系水生态功能保护具有十分重要的意义，在百泉争涌的主城区流域，地下水是基流主要来源，同时也存在人类活动用水的排放(这部分径流量虽较小，但实质并非基流，本文为计算便捷，统一将其划归为基流)，基流占洪峰流量的比例较大(可能超过20%)，对济南市水文过程模拟和流域产汇流计算影响较大[13,27-28]。因此，本文尝试从不确定性分析角度探索基流分割对城市雨洪模拟不确定性的影响。

根据研究区地表地下水交互频繁、包气带较厚等水文地质特征选取传统且适用性较强的水平分割法来进行基流分割，其分割方法如下：绘制洪水流量过程线，过程线中流量最低值为基流值，并藉此划分水平基准线，基准线以下流量即为基流，以上流量为暴雨过程产生的径流量[28-29]。因城市雨洪过程的复杂变异性，所以每次模拟洪水过程前需重新分割基流。

3 结果与分析

为获取代表性更强的参数集，本文利用改进的蒙特卡罗法，即拉丁超立方采样法获取1万组参数组合，并运行模型模拟各暴雨场次洪水流量过程[30]。将RMSE设为似然函数，将25 m3/s设为似然函数阈值，并根据有效参数组合的模拟结果，归一化处理其似然值，计算累积概率分布函数(cumulative distribution function，CDF)。

3.1 城市雨洪模拟不确定性分析

7场洪水资料的基流分割结果见表1，基流占洪峰流量比例均超过10%，但变化不大，基本在10%～20%之间波动，均值为13.38%。图2中灰色区域表示1万组参数产生的流量过程模拟总不确定性区间，两组流量序列在总不确定性区间的覆盖率CR分别为61.23%和95.65%，基流分割后流量序列基本覆盖在区间内，覆盖效果良好，但原始流量序列的覆盖率相对较小，图2可清晰看出未覆盖的点主要集中在峰后流量过程，表明无论如何调节参数，这部分流量过程的模拟效果始终较差，原始流量序列作为模型校验数据的可靠性有待进一步考证。

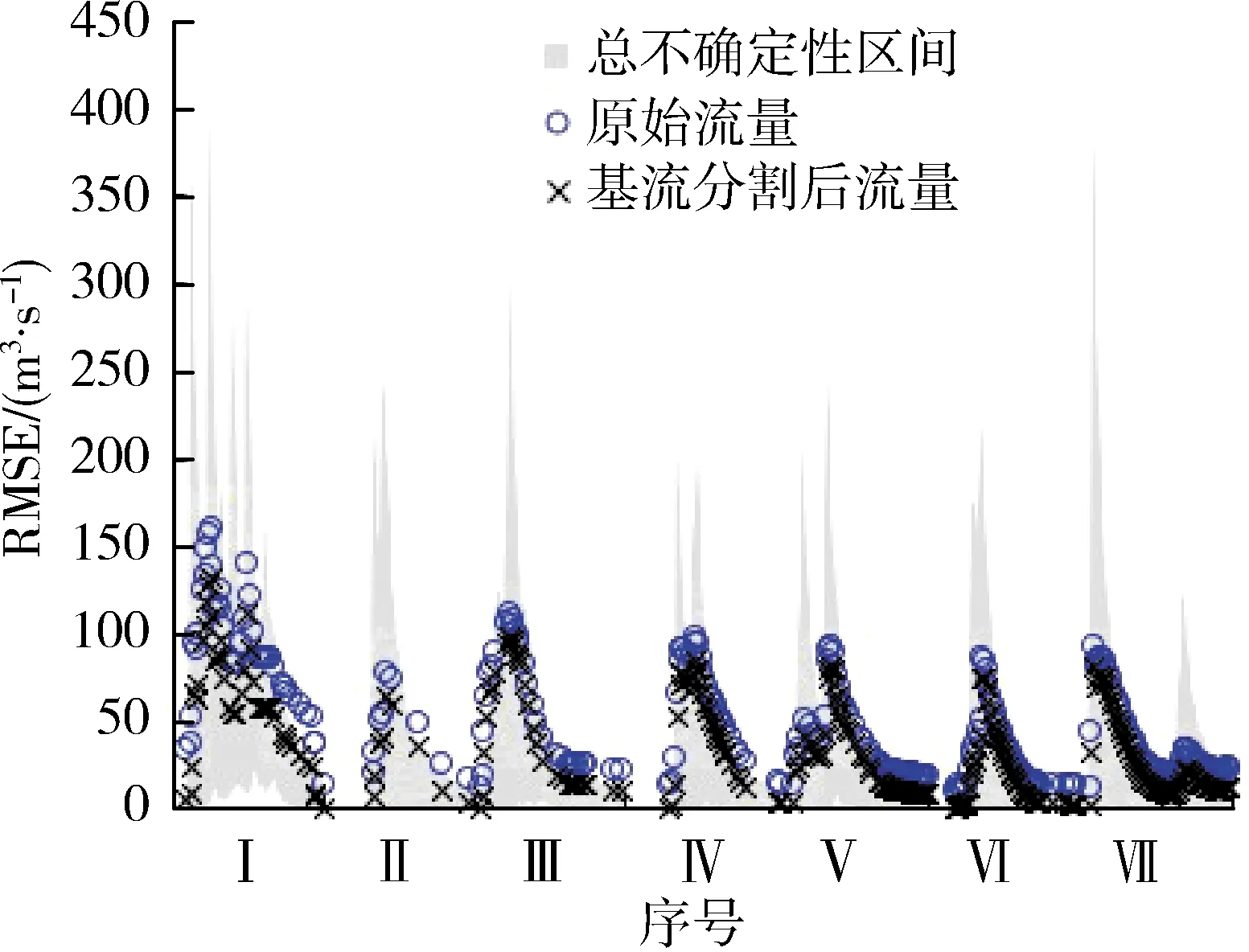
图2 洪水流量过程线

表1 7场洪水基流分割结果

出现上述现象的原因可能是，原始流量中基流占比较大，基流一般是河道中常年存在且较为稳定的流量，与暴雨并无直接关系。直接使用原始流量作为模型校验数据，忽略了流量中并非来源于场次降水的基流组分，显著增大了雨洪模拟的不确定性。从模型结构来看，城市雨洪模型较传统水文模型有所不同，模拟时长较短，一般用于场次暴雨洪水模拟，且主要刻画暴雨前后短时间水文过程，很难考虑基流在模拟中的影响[18-19]。主城区流域属济南市地下水系排泄区，泉水成为城市河道基流的主要水源，独特的水文地质特征使得济南市河道流量中基流占比相对较高，丰沛的泉水增强了基流对模拟效果的影响[13]。因此，当使用流量序列作为雨洪模型校验数据时，基流的存在不可忽视，有必要对流量序列进行基流分割。

图3是以基流分割前后两组流量序列为模型校验数据，所有参数集模拟流量过程的似然函数累积概率密度分布图。从图3可以明显看出，基流分割后流量序列概率密度值始终位于原始流量序列上方，两组流量序列计算的RMSE值低于阈值25 m3/s的有效参数组合数分别为284组和2 494组，最小值分别为19.15 m3/s与13.70 m3/s。基流分割后流量序列计算的RMSE主要集中在15～40 m3/s之间，原始流量序列的计算值主要集中在20～55 m3/s之间。不论是RMSE最小值，还是有效参数组合数，应用基流分割后流量序列作为校验数据的模型模拟效果明显优于原始流量序列，基流的存在对模型校验的影响较为明显。

图3 似然函数累积概率密度分布

图4为1万组参数组模拟结果似然值散点图，可以清晰地看出两组流量序列的低似然值区，同时存在多组等效参数组合，表明GLUE方法能够很好地解释“异参同效”现象，即对同一评价指标而言，可存在多组参数组合的模拟效果一致。在预警预报中，同时使用多组有效参数组合模拟洪水过程并进行分析讨论，能够有效规避传统思想认为的有且仅有一组“最优参数组合”带来的预报风险，使模型具有更强的稳健性[26]。两组流量序列计算的RMSE也存在明显差异，原始流量序列计算的RMSE不确定性范围更加离散，且RMSE总体大于基流分割后的流量序列。上述现象表明，当应用流量序列校验模型时，基流分割能够明显收敛模拟结果的不确定性，并提高模拟精度。基流分割后流量序列具有较强的可靠性，可作为城市雨洪模拟的校验数据。

图4 1万组参数组模拟结果似然值散点图

3.2 90%置信区间不确定性分析

似然函数RMSE高于阈值的参数组合不能有效反映流域水文特征，将其似然值统一设为0。低于阈值的参数组合，重新归一化处理其似然值，并按照大小进行排序，求出一定置信度下的模拟预报不确定性区间。本文将置信度设为90%，模拟结果如图5所示。

由图5可知，原始流量序列趋势与90%置信区间基本一致，基流分割后流量序列落入90%置信区间点数明显高于原始流量序列，且大部分实测流量值落入置信区间内，表明本文构建的SWMM模型在主城区流域模拟城市雨洪过程效果较好。由图5(a)可以明显看出，大部分峰后流量过程依旧落在90%置信区间之外，而通过基流分割后(图5(b))，峰后流量过程基本落在90%置信区间内，模拟效果明显提升。表明基流的存在明显增大了模拟结果的不确定性，且基流的存在对峰后流量过程模拟影响较大。

(a)原始流量序列

两组流量序列置信区间估计评价结果如表2所示，可以看出，基流分割后流量序列实测值区间覆盖率CR高达68.12%，较原始流量增大100%，但区间平均宽度RB明显高于原始流量序列，增大了0.58，随着CR增长RB也呈增长趋势，这个结论与Xiong等[25-26]的结论一致。在对称性方面，基流分割后流量序列不确定性区间计算的平均偏移幅度D和平均对称度S明显低于原始流量序列，平均偏移幅度和平均对称度分别减小了42.60%和87.19%，不确定性区间对称性明显提高。综合分析4项指标可知，在同等置信度下，基流分割后流量序列的预测不确定性区间覆盖率与对称性明显优于原始流量序列，且不确定性区间的性能更加优良，可靠性更高。

表2 不确定性区间评价结果

4 结 论

a.在济南市主城区流域，当使用流域出口流量序列校验雨洪模型时，7场洪水基流占洪峰流量的比例较大，均超过10%。基流分割前后流量序列在模拟结果总不确定性区间覆盖率分别为61.23%和95.65%，基流的存在对城市雨洪模拟影响较大，特别是对峰后流量过程模拟的影响最明显，原始流量序列作为模型校验数据的可靠性较差。

b.应用原始流量序列和基流分割后流量序列校验模型时，1万组参数组中满足似然函数阈值的有效参数组合数分别为284组和2 494组，RMSE最小值分别为19.15 m3/s与13.70 m3/s。应用基流分割后流量序列作为校验数据的模拟效果明显优于原始流量序列，且似然值分布区间更加集中，即基流分割后流量序列作为模型校验数据的可靠性更强。

c.相较于原始流量序列，使用基流分割后流量序列模拟的流量90%置信区间覆盖率增大100%，平均偏移幅度和平均对称度分别减小42.60%和87.19%，使用基流分割后的流量数据校验模型，能够有效降低流量序列导致的模拟结果不确定性，可提供更精确对称的流量预报区间。