Delta算子框架下大系统的协同控制研究
薛艳梅 韩金珂
0 引言
随着计算机、通信等技术的飞速发展,复杂大系统(Large Scale System)已广泛应用在工程技术[1-4]、社会经济[5]、生态环境[6-8]等各个领域.大系统的特点是模型维数较高、结构复杂、对系统鲁棒性要求较强等.大系统稳定性研究常用局部反馈方法,通过减少子系统间的互联增加大系统稳定性[9].但文献[10-11]的研究表明互联和协同在大系统稳定性中也有重要作用.文献[10]在自反馈和互联反馈情况下,给出两个系统协同稳定的充要条件,提出两系统谐波控制的概念;文献[11]针对含有不稳定子系统的大系统,设计一种特殊的分散控制器,使其通过有效的协同成为稳定的互联系统;文献[12]针对多无人机系统,在分析最优布站方式基础上,提出一种闭环最优控制方法,有效提升了多机协同跟踪时差无源定位的精度;文献[13]则针对航空火力系统,研究了分布式协同架构下的控制问题.
离散时间系统可由连续时间系统采样得到,适用于计算机实现,但当采样快时在有限字长的计算机中并不稳定.离散时间模型常用移位算子的形式表示,但在短采样周期间隔下存在截断和舍入误差困难的问题.在采样周期趋近于0时,离散Delta算子模型趋近于原连续模型,能有效克服移位算子方法高速采样时的缺点,有效避免传统Z变换引起的数值不稳定问题,使得连续域的各类设计方法可直接应用于离散域.因此Delta算子已成为连续时间模型和离散时间模型的统一描述方法,在计算机高速信号处理、宽带通信与数字采样控制领域具有广阔的应用前景[14].目前关于Delta算子的研究多集中在数据丢包、时变时延、H∞滤波等方面[15-19].文献[15]针对二维Delta算子系统在饱和状态下的稳定性问题,给出了系统极限轨迹的一般性质和全局渐近稳定的充分必要条件;文献[16]针对Delta算子系统设计一个多频率区间降价H∞滤波器,降低了现有方法的计算复杂度并提高了H∞性能;文献[17]针对具有双通道丢包、时变时延且范数有界的不确定Delta算子网络控制系统,提出一种基于交换系统的故障检测方法,并给出了期望滤波器参数的显式表达式;文献[18]将交换拓扑网络中具有协作竞争交互和通信时延的多智能体系统的群一致性问题,转化为具有通信时延系统的全局渐近稳定问题;文献[19]针对具有内部参数摄动和外部干扰的高速信号采样系统,提出一种基于Sigmoid函数的Delta算子饱和变速趋近律,实现了不确定Delta算子系统的软滑模控制器设计.
值得注意的是,关于Delta算子的大系统协同控制方面的研究较少.文献[9]将一些连续系统或离散系统的结果整合到Delta算子框架下,通过李雅普诺夫稳定性理论以线性矩阵不等式形式给出了大系统协同稳定的充分条件.
受上述研究启发,本文将Delta算子描述的大系统看作相互独立的子系统,研究Delta算子框架下线性大系统的协同状态反馈控制问题.以线性矩阵不等式形式给出了互联系统协同状态反馈渐近稳定的充分条件,并给出了优化性能指标.本文方法放宽了文献[9]中协同状态反馈控制器设计中对正定矩阵的约束条件,使结果更具一般性.最后仿真实例进一步验证了本文算法的有效性及优越性.
1 预备知识及问题描述
1.1 预备知识
文中Rp×q表示p行q列的实矩阵,AT表示矩阵A的转置,M-1表示矩阵M的逆.A>0表示A为对称正定矩阵,A≥0表示A为对称半正定矩阵.
定义1[14]Delta算子定义如下:
其中,T表示一个采样周期.

引理1[14](Delta算子的性质) 对任意关于时间t的函数x(t)和y(t),有
δ(x(t)y(t))=δ(x(t))y(t)+x(t)δ(y(t))+
Tδ(x(t))δ(y(t)).
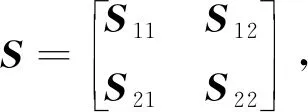
1)S<0;
1.2 问题描述
本研究考虑Delta域下独立子系统通过协同控制成为一个互联闭环系统的状态反馈控制问题.
Delta算子描述的两个独立子系统如式(1)、(2)所示:
δ(x1(tk))=Aδ1x1(tk)+Bδ12u12(tk),
(1)
δ(x2(tk))=Aδ2x2(tk)+Bδ21u21(tk),
(2)
其中,x1(tk)∈Rn1和x2(tk)∈Rn2分别表示子系统1与子系统2的状态,u12(tk)∈Rm1和u21(tk)∈Rm2分别表示子系统1和子系统2的控制输入,子系统1和子系统2的系统矩阵分别为Aδ1∈Rn1×n1和Aδ2∈Rn2×n2,控制输入矩阵分别为Bδ12∈Rn1×m1和Bδ21∈Rn2×m2均为已知常值矩阵.
为使大系统协同稳定,首先根据子系统(1)、(2)构造状态反馈协同控制器[9,11]:
u12(tk)=Kδ12x2(tk),
(3)
u21(tk)=Kδ21x1(tk),
(4)
其中Kδ12∈Rm1×n2,Kδ21∈Rm2×n1是将要设计的状态反馈增益矩阵.
联立(1)—(4),可以得到闭环系统:

(5)
定义2[11]如果存在协同状态反馈控制器(3)—(4),使得闭环系统(5)渐近稳定,那么系统(1)—(2)就是协同状态反馈稳定的.
本文进一步考虑如下协同控制器性能指标[9]:
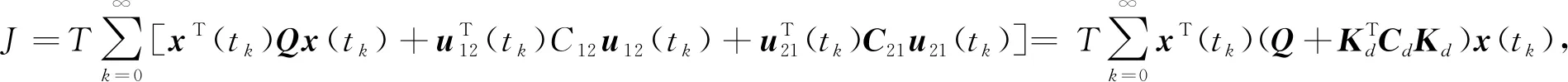
(6)
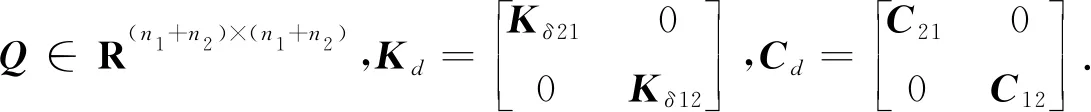
定义3如果存在协同状态反馈控制器(3)—(4),使得闭环系统(5)渐近稳定,并满足性能指标(6),那么子系统(1)—(2)就是协同状态反馈稳定,并具有性能J.
针对系统(1)—(2),求取Kδ12,Kδ21,使得协同控制器(3)—(4)作用下的闭环系统(5)渐近稳定的控制问题是协同状态反馈控制器设计的可行性问题.设计方法如文中定理1所示.
针对系统(1)—(2),求取Kδ12,Kδ21,使得协同控制器(3)—(4)作用下的闭环系统(5)渐近稳定,并满足性能指标J的控制问题是协同状态反馈控制器设计的优化问题.设计方法如文中定理2所示.
2 主要结论
2.1 协同控制器设计的可行性问题
定理1如果存在正定矩阵X11∈Rn1×n1,X22∈Rn2×n2,W11∈Rn1×n1,W22∈Rn2×n2和矩阵X12∈Rn1×n2,W12∈Rn1×n2,Y11∈Rm2×n1,Y12∈Rm2×n2,Y21∈Rm1×n1,Y22∈Rm1×n2,使得:
(7)
成立,其中
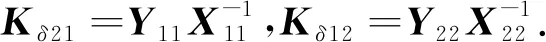
证明建立δ域的李雅普诺夫函数:
V(x(tk))=xT(tk)Px(tk).
(8)
结合引理1、李雅普诺夫函数(8)及表达式(5),可以得到:
δV(x(tk))=δT(x(tk))Px(tk)+
xT(tk)Pδ(x(tk))+TδT(x(tk))Pδ(x(tk))=
TδT(x(tk))Pδ(x(tk)).
(9)
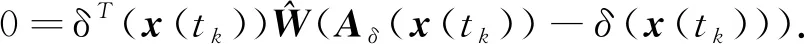
(10)
将式(10)代入式(9)中可以得到:
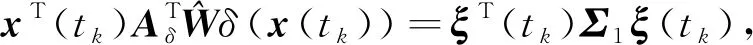
(11)
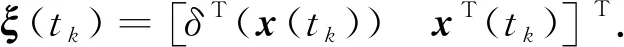
由式(11)可知,δV(x(tk))<0 成立的充分必要条件是

(12)
(13)
根据引理2,上述矩阵不等式(13)成立等价于
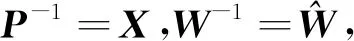

(14)
将式(5)中的矩阵Aδ代入式(14),并令Kδ21X11=Y11,Kδ12X22=Y22得到
进一步可知,当上述线性矩阵不等式Σ<0时,式(12)也成立.进而
可知在x(tk)≠0时,下述不等式成立:
xT(tk+T)Px(tk+T)-xT(tk)Px(tk)<0.
(15)
这就是说李雅普诺夫函数xT(tk)Px(tk)在δ域中是严格减函数.因此可以得到
xT(tk)Px(tk)→0,k→0.
又因为矩阵P>0是一个常数矩阵,有
x(tk)→0,k→0.
由此可知,在线性矩阵不等式Σ<0成立的情况下,系统(1)—(2)是协同状态反馈稳定的.定理1得证.
2.2 协同控制器设计的性能优化问题
定理2如果存在正定矩阵X11∈Rn1×n1,X22∈Rn2×n2,W11∈Rn1×n1,W22∈Rn2×n2,Z11∈Rn1×n1,Z22∈Rn2×n2和矩阵X12∈Rn1×n2,W12∈Rn1×n2,Z12∈Rn1×n2,Y11∈Rm2×n1,Y12∈Rm2×n2,Y21∈Rm1×n1,Y22∈Rm1×n2,使得线性矩阵不等式:
(16)
成立,其中
J≤xT(t0)Px(t0).
(17)
证明如定理1所示,取δ域上的李雅普诺夫函数为
V(x(tk))=xT(tk)Px(tk).
结合式(9)与式(10),令

(18)
即
ξT(tk)Π1ξ(tk)<0,
(19)
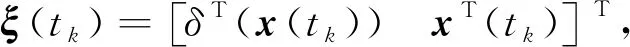
(20)

(21)
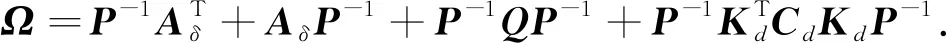
根据引理2,上述矩阵不等式(21)等价于

(22)
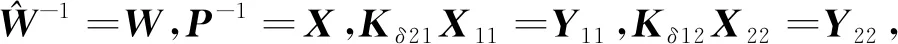
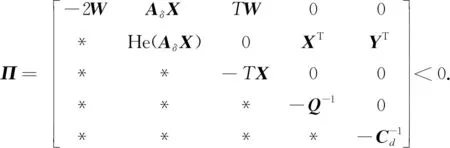
(23)
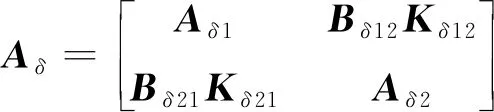
由此可知,Π<0当且仅当Π1<0.
进一步,对于任意整数k>0,对式(18)两边同时乘采样时间T,并从0到kT进行求和,可以得到
即
J≤xT(t0)Px(t0),
此时定理2得证.
综上所述,定理1和定理2以线性矩阵不等式形式,分别给出了状态反馈协同控制器的可行性设计方法和状态反馈协同控制器的优化设计方法.
注2相比于文献[9]的方法,本文放宽了等式(10)中正定矩阵必须与线性矩阵不等式中正定矩阵相同的要求,即,原文中引入
0=δT(x(tk))P(Aδ(x(tk))-δ(x(tk)))
而不是
进一步,下述定理3给出了最优性能J的控制设计方法.
定理3对于给定的系统(1)—(2)和性能指标(6),如果以下的优化问题
minγ
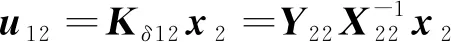
证明与定理2相比,条件(ⅰ)—(ⅳ)是相同的.由定理2,令J≤xT(t0)Px(t0)<γ,应用引理2,并注意到P-1=X,易得条件(ⅴ).定理3得证.
3 数值仿真
本节将通过Matlab软件平台的Simulink进行仿真,验证所提定理的有效性.
考虑Delta算子描述的独立子系统参数取值如下:
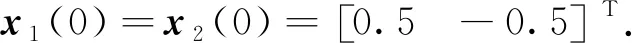
通过表1比较可以看出,本文的设计方法比文献[9]中的方法在求解方法上保守性更低.
根据本文定理1可得到可行解Kδ12,Kδ21分别为

表1 四种控制方法比较
根据本文定理3可求得优化的性能指标J=5.000 7.此时可以得到最优解Kδ12,Kδ21为
经Matlab-Simulink仿真,两个子系统协同控制下的状态仿真结果分别如图1与图2所示.由仿真结果可以看出本文提出的可行性方法以及优化方法均能使得系统状态在很短时间内收敛到0,有效实现协同稳定的控制效果.
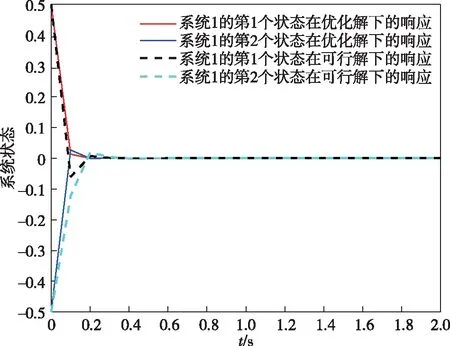
图1 子系统1在协同控制下的状态仿真结果Fig.1 State simulation results for the first subsystem under cooperative control
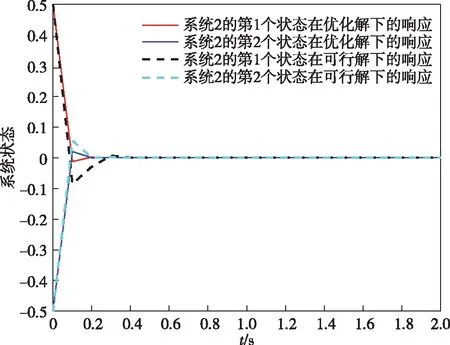
图2 子系统2在协同控制下的状态仿真结果Fig.2 States simulation results for the second subsystem under cooperative control
进一步,比较两个子系统的状态响应结果图1—2与控制输入响应结果图3—4,可以看出,优化算法下的状态会收敛更快且需要耗费的控制输入成本更少.
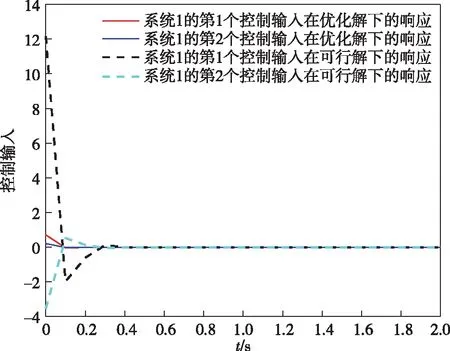
图3 子系统1在协同控制下的控制输入仿真结果Fig.3 Control input simulation results for the first subsystem under cooperative control
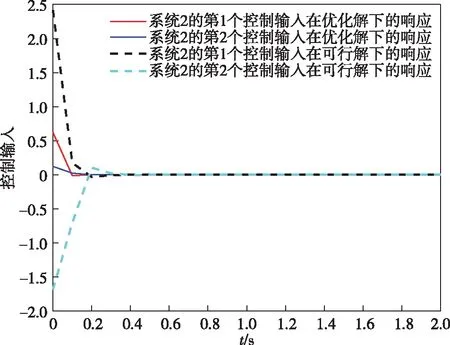
图4 子系统2在协同控制下的控制输入仿真结果Fig.4 Control input simulation results for the second subsystem under cooperative control
4 结束语
本文提出的基于Delta算子框架的线性大系统协同稳定的充分条件,使得含有不稳定子系统的大系统协同稳定的同时放宽了已有研究控制器设计中对正定矩阵的约束条件.根据李雅普诺夫稳定性理论证明了所提方法的有效性及优越性.仿真结果表明,本文所设计的协同控制器可以确保系统稳定运行.

