提高数学课堂教学效率的探索

许志超

（德化第一中学鹏祥分校 福建泉州 362500）

一、课堂教学融汇数形结合思想

数学离不开数和形，它们紧密联系、互相依赖，可相互转化。数辅助形、形帮助数，有助于寻找解题思路时直观形象，能做到优化解题思路。

例：y=x2+(1-a)x+1(1≤x≤3)是关于x的二次函数，y在x=1时取得最大值，求a的取值范围。

分析：y=x2+(1-a)x+1图象的位置随着a的变化而变化。我们知道几何画板软件是“数形结合”思想体现的有力工具，函数图象的动态演示既直观又形象，从动态演示可知，该二次函数在取值范围内的最值可分三种情况讨论。选择几何画板动态演示下的三幅静态图，画示意图如下：

方法一：观察图①，函数值y是递增的，观察图②，此时图象两端点关于直线x=2对称，观察图③，y值是递减的，所以只要时，y值最大，因此有方法一：，解得，a ≥ 5。

①

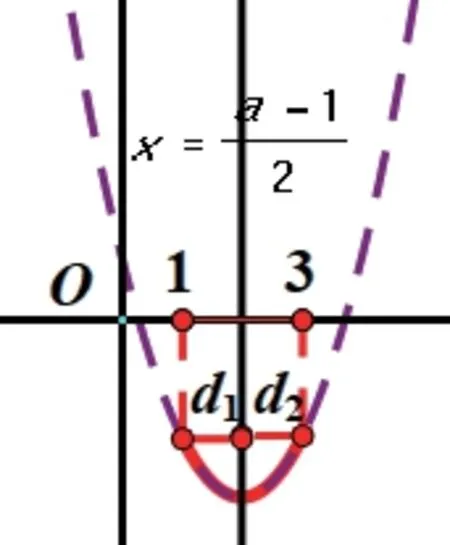
②

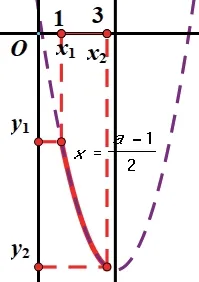
③

方法二：观察图象①、②、③，函数图象的端点到对称轴距离远的，函数值y就取得最大值；特别的，当x=1和x=3时的函数图象端点到对称轴的距离一样远，函数值y在x=1和x=3时，都取得最大值。因此可列如下不等式：解得，a≥5。

方法三：观察图象①不符合题意，图象②、③符合题意，可算出图象两端点的y值y1=1+(1-a)+1=3-a，y2=9+3(1-a)+1=13-3a，所以只要3-a≥3-3a时，符合题意，解得a≥5。

总之，几何画板能创设“数形结合”情景，让抽象、枯燥的数式转化成了图形实验环境，选择几何画板动态演示下的不同情形静态图，能把已知条件和结论转化成直白的图象关系，从而使数学解题方法更加优化。

二、课堂教学生活化

数学来源于生活，与生活密不可分。数学是有趣的，我们可以在游戏中用数学、学数学。同学们喜欢充满乐趣的“生活数学问题”，因此课堂教学可以从“生活中的数学”入手[2]。

例：中国历史上有一个脍炙人口的“田忌赛马”故事，这是赛马赌胜的“三局两胜制”游戏。该游戏有两方参加比赛，一方是齐王的上、中、下三匹马X1、Y1、Z1，另一方是田忌的上、中、下三匹马X2、Y2、Z2，可用不等式表示这些马比赛胜负：X1＞X2＞Y1＞Y2＞Z1＞Z2（注：X＞Y表示X、Y马比赛，X马胜）。田忌在劣势的情形下，采纳了他身旁孙膑的办法对阵：即对阵（X1Z2，Y1X2，Z1Y2），田忌胜出。现在，齐王首局出“下马”被田忌知道了，那么他获胜的机会是多少？可分析如下：

第一局出马情况为Z1Y2，田忌获胜；

那么比赛所有等可能的对阵为：（Z1Y2，X1X2，Y1Z2），（Z1Y2，X1Z2，Y1X2），（Z1Y2，Y1X2，X1Z2），（Z1Y2，Y1Z2，X1X2），共四种等可能情况，其中获胜的有以下两种（Z1Y2，X1Z2，Y1X2），（Z1Y2，Y1X2，X1Z2），∴P（田忌获胜）=。

学生们通过对“田忌赛马”故事的有趣思考、乐于思考，对引入参数、不等式概念、必然事件、不可能事件及随机事件概率有了更深的理解，数学中零星的知识串在了一起，增强了数学知识点之间的联系，使得数学知识融会贯通，促使他们热爱数学，乐学数学，知道了日常生活中的许多事蕴含着数学道理。

三、课堂教学运用转化与联想，一题多解，培养发散思维

“转化与联想”是初中数学解题的核心思想，它能够激活学生思维，扩展思路，能有效避免学生学习数学死记硬背公式、生搬硬套的呆滞做法，能用已有的知识经验去解决难度较大的数学问题，下面通过典型例题解析“转化与联想”解题方法的应用。

（1）求证：∠P=45°

（2）在（1）的条件下，作DN⊥GP于点N，连接CN、BP，取BP的中点M，连接MN，求证：

（1）解法分析如下

方法一：欲证∠P=45°，连接BD交GP于Q时，∠GBQ=45°，又在△GBQ与△DPQ中，∠GQB与∠DQP是一组相等的对顶角，所以结论成立时，有△GBQ～△DPQ。反过来，要证△GBQ～△DPQ，只要证∠BGQ=∠PDQ。

题目的已知条件AG=BF=EF要如何用呢？

设AG=BF=EF=a，BG=b，

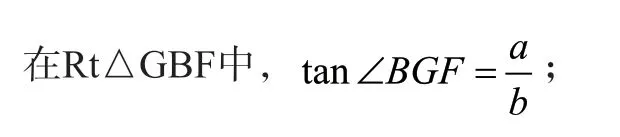
在斜三角形QDP中，过点E作EH⊥BD于H，

所以∠BGQ=∠PDQ。

方法二：欲证∠P=45°，联想到过点F作FI‖PD交AD于I，∠P可转化∠GFI，因为AD‖BC，所以四边形IDEF是平行四边行，所以ID=EF=BF=AG；在正方形ABCD中，AD=AB，∠A=∠B=90°，所以AI=BG；又联想到连接GI时，可证△AGI ≅△BFG(SAS)，所以GI=GF，∠1=∠3。又因为∠1+∠2=90°，所以∠2+∠3=90°，所以∠FGI=180°-（∠2+∠3）=90°，所以△GFI是等腰直角三角形，所以∠GFI=45°，所以∠P=45°。

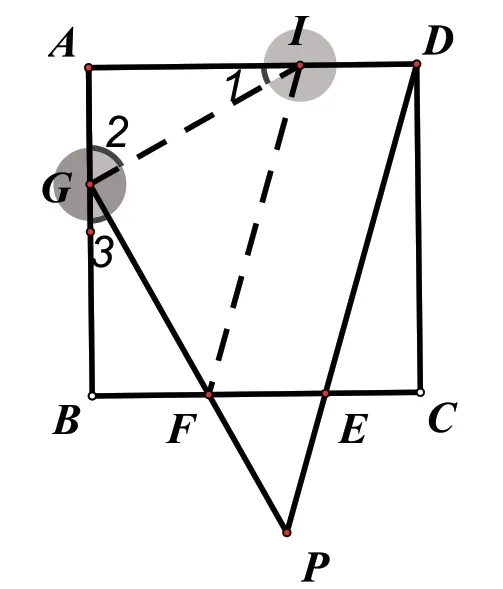
点评：在解数学题时，不是一审题，就马上有思路，一些问题的思路是在对问题条件和结论的不断转化中得出来的，在已有知识经验的基础上进行丰富联想得出来的。在解决数学问题时，运用联想和转化，解题效率会大大提高。

（2）解法分析如下：

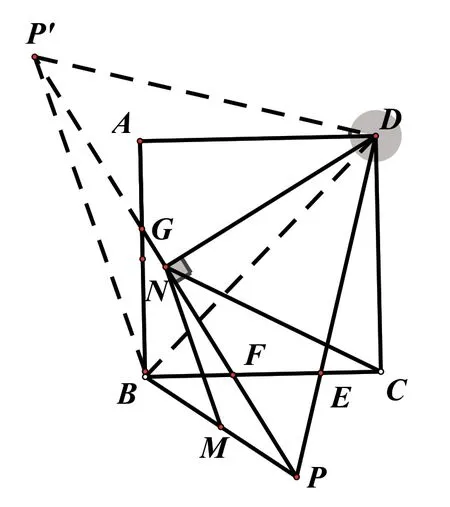
方法二：考虑在图形内作辅助线，由∠NPD=45°，DN⊥PN可知△PND是等腰直角三角形，联想到试着作NQ⊥PD于Q，则PQ=QD，又BM=MP，联想到三角形中位线，连接MQ、BD。观察图形，欲证可证△MNQ～△CND，那么可转化为

点评：正向、逆向思维相结合，善于挖掘图形的特殊性，在联想中渗透转化思想，把综合强的问题转化分解为几个基本问题，让学生亲身体验转化过程，将数学知识紧密联系，形成脉络，有利于提高学生的数学解题能力。

四、课堂教学引导学生探究数学模型

例：如图，OP平分∠AOB，OC=OD，连接PC、PD，试说明△PCO ≅△PDO.

分析：易证△PCO ≅△PDO(SAS)

又当PC‖OD时，四边形PCOD是菱形；

当PC⊥OA时，四边形PCOD是菱形；

当PC⊥OP时，△CDO是等腰三角形。

这就是角平分线的相关模型，我们可以利用其中的模型启发解题思路。比如：如图，∠ABC=45°，PB平分∠ABC，PD⊥BC于D，若BD=3，则PD的长是多少？分析：欲求PD，可作PE⊥AB于E，构造角平分线模型，则PD=PE，延长DP交AB于F，则DF=BD=3，

设DP=PE=X，则在Rt△PEF中，∠EFP=45°，

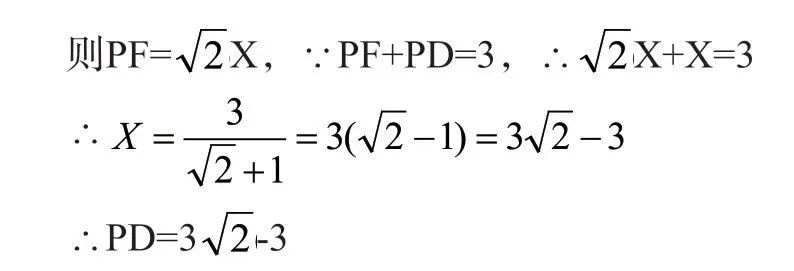
运用模型思想进行数学教学，有利于学生从思维的“已有经验”出发探寻解题思路，培养学生的数学解题模型思维，避免解题容易出错，解题速度慢等问题。