自然对流对方腔内相变石蜡熔化蓄热的影响

陈俊旗，曹世豪

(河南工业大学土木工程学院，郑州 450001)

伴随电子产业发展带来便利的同时，其工作过程中的发热量随着系统集成度的提高而增大，如不能及时散热，将会影响电子器件的工作甚至失效[1]。相变材料(phase change material,PCM)在固-液相变过程中可以储存或释放大量能量，相对于基于显热储能的传统材料，不仅具有更高的储热效率，且相变过程中温度基本保持不变。采用相变材料制成的相变散热器，在防止电子器件瞬变、间歇性过热失效方面具有极大的应用潜力[2]。同时，相变材料也被逐渐应用于房屋建筑节能、太阳能热发电、电子元器件冷却及食品冷藏保鲜运输等多个领域[3-6]。

目前，常见的相变材料根据其熔化温度可分为低温(-50～90 ℃)、中温(90～550 ℃)、和高温(>550 ℃)三类，而根据其化学成分可分为无机类、有机类和复合类三种。有机低温相变石蜡因具有熔凝循环稳定、无腐蚀及无过冷等优点吸引了大量学者研究[7-8]。Madruga等[9]采用多孔介质模型，以熔化分数来控制熔化储热过程中的相态变化，随后结合VOF (volume of fluent)模型实现了热毛细流影响分析。为了消除温度梯度所致浮升力的高度非线性问题，学者采用Boussinesq假设将浮升力转化为与温度线性相关的体积力[10-11]。针对相变石蜡热传导系数小储能慢的缺陷，学者通过采用泡沫金属、纳米金属颗粒改性及有效利用自然对流等方法提高储能效率[12-14]。Cao等[15]、Madruga等[16]研究发现，液相石蜡的自然对流传热效应存在显著的尺寸效应。相变材料所处容器的形状也是影响其熔化蓄热性能的重要因素之一。在过去几十年中，许多学者针对球形、圆柱形、矩形、半圆形以及各种不规则形状的相变材料熔化蓄热性能开展了大量研究[17-20]。目前，底边热源下的方形腔体内相变材料熔化蓄热特性关注较少，而该形态蓄热装置在电子设备控温领域具有较好的应用前景[1,21]。

为此，针对自然对流对方腔内的相变石蜡熔化蓄热性能的影响开展理论与试验研究。首先基于Boussinesq假设修正满足于相变过程的动量方程，并建立相变材料熔化蓄热的流-固-热三场耦合计算模型。随后采用有机相变石蜡材料，开展底部恒定温度下的石蜡熔化蓄热试验，验证计算模型的正确性。最后使用验证后的计算模型，对底部恒定温度下方腔内相变石蜡储热过程进行分析，明确相变石蜡熔化蓄热过程中的热传导与自然对流传热竞争作用机制，获得液相自然对流传热的尺寸效应及临界阈值，为相变储热系统设计中合理的利用对流传热效应来提升蓄热效率提供理论依据。

1 相变石蜡熔化蓄热试验

在底部恒温条件下，测定相变石蜡的熔化储热特性试验装置，如图1所示。试验装置由方腔容器、相变石蜡、加热板、高导铜板、热电偶、多路温度采集仪及摄像机等组成。方腔容器截面尺寸为100 mm×100 mm，厚度为10 mm，由隔热性能较好的高透明PVC塑料制成，便于观察记录相变石蜡的熔化过程。相变石蜡由上海焦耳蜡业有限公司提供，熔点为300 K，对应的其他热物理参数如表1所示。试验前，相变石蜡需静置于实验室环境下不少于24 h，以此获得较为均匀的初始温度，本试验的初始温度约为16 ℃。试验中的底部恒定热源Tw为70 ℃，由硅胶加热板自带的数显温度控制器控制，精度为±1 ℃。为了使热源温度更加均匀，在加热板上粘贴一层厚度为2 mm的高导热铜板。使用4个K型热电偶(精度±0.1 K，间隔20 mm)实时监测相变石蜡熔化过程中的温度变化。相变石蜡动态熔化前缘通过摄像机拍照记录，拍照间隔为10 min。

表1 热物理参数Table 1 Thermal physical parameters

由试验测试结果(图2)可知，在底部恒定温度热源下，初期的相变石蜡熔化前缘基本呈直线，且与底部热源保持平行，如图2(b)所示。随着熔化的继续，熔化前缘逐渐转变为周期性分布的波浪形，波浪形熔化前缘的形成与液相层自然对流运动传热直接相关。如图2(c)所示，在液体分数f=0.034时(对应的液相层厚度为3.4 mm)，单个波浪形熔化前缘的波长约为4 mm。随着熔化的持续进行，相邻的周期性短波逐渐融合为较大的无规则长波，如图2(d)～图2(f)所示。在相变石蜡熔化储热的后半段，熔化前缘逐渐转化为一个长波和若干短波共存的形态，并持续至试验结束。

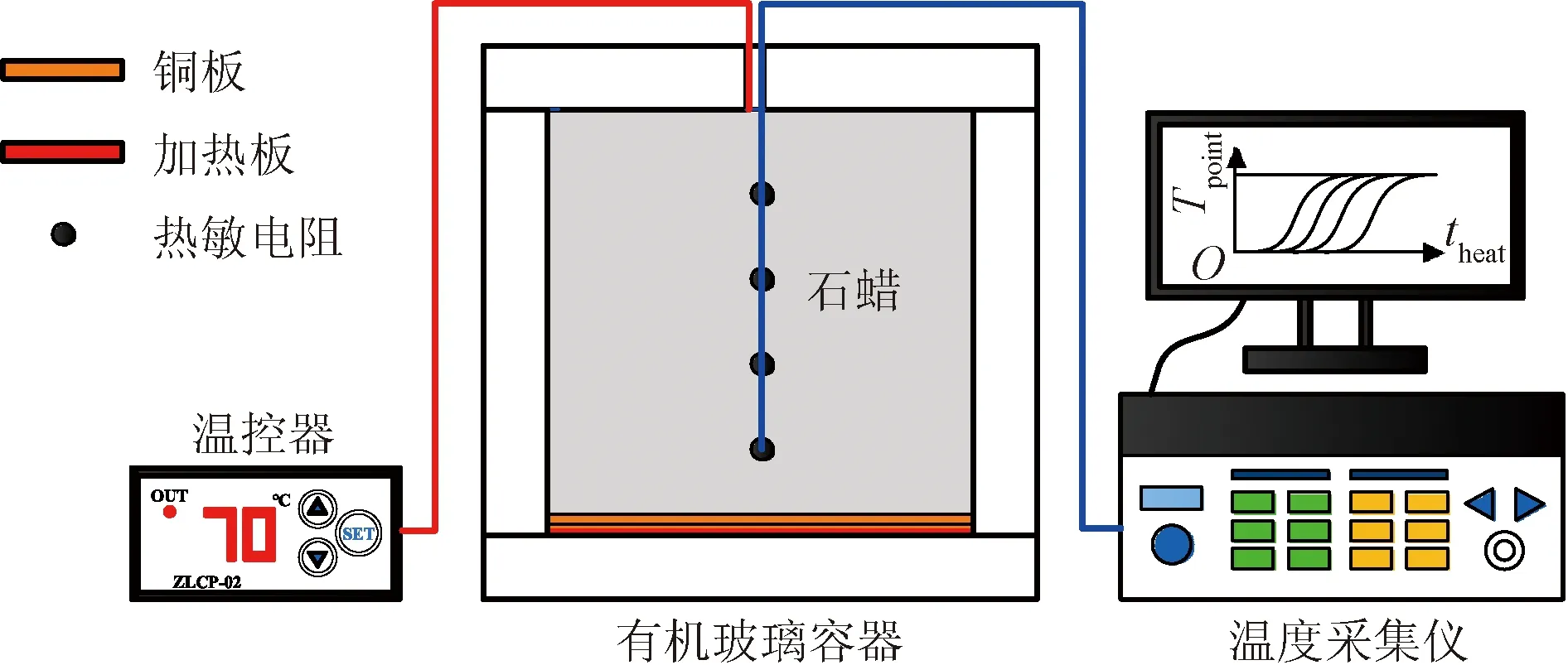
Tpoint为热电偶记录的测点温度；theat为加热时间图1 相变石蜡熔化试验装置Fig.1 Melting test setup of phase change paraffin

图2 不同液体分数对应的石蜡熔化前缘形态Fig.2 Shapes of paraffin melting front at different liquid fraction

2 计算原理

由试验测试结果(图2)可知，相变石蜡熔化过程中包含了热量传输、固液相变、液相流动等过程，表明真实的相变石蜡熔化蓄热过程是个极为复杂的流-固-热三场耦合问题。该过程需同时满足质量守恒、动量定理及能量守恒3个控制方程。

连续性方程为

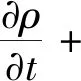
(1)

动量方程为

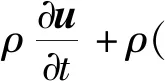
(2)

能量方程为

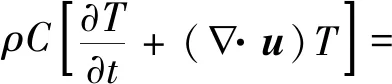
(3)

式中：ρ为密度；t为时间；∇为哈密顿算子；u为速度矢量；p为压强；I为单位向量；μ为动力黏度；g为重力加速度；F为体积力矢量；C为比热容；T为绝对温度；q为热通量向量；τ为黏性力张量；S为应变率张量；α为热膨胀系数。

体积力F是液相密度差所引起的浮升力，当温度变化引起的液相密度波动很小时，该浮升力可采用Boussinesq假设近似表示为

F=-ρ[1-α(T-Tref)]g

(4)

式(4)中：Tref为参考温度，计算中取Tref=Tm，其中Tm为熔化温度。

为了提高计算收敛性，假定相变石蜡熔化过程发生在温度区间ΔT内，一般取ΔT=1 K。TTm+0.5ΔT时，石蜡为液体；Tm-0.5ΔT≤T≤Tm+0.5ΔT时，石蜡为固液混合物。则各相与液体分数f的关系可表示为

(5)

相变石蜡在熔化储热过程中，对应的热物理参数在相态转变过程中发生着变化。本文假定固、液相态时材料的热物理参数保持不变，混合相态时热物理参数是温度的线性函数。结合式(5)，可建立等效导热系数k、ρ及等效比热容C与液体分数f的关系，可分别表示为

k=(1-f)ks+fkl

(6)

ρ=(1-f)ρs+fρl

(7)

(8)

式中：ks和kl分别为固相和液相的导热系数；ρs和ρl分别为固相和液相的密度；Cs和Cl分别为固相和液相的比热容；β为质量分数，可表示为

(9)

3 计算模型

基于上述控制方程，采用COMSOL软件，建立了底部恒定温度下方腔内相变石蜡熔化蓄热的流-固-热三场耦合计算模型，如图3所示。模型为100 mm×100 mm正方形，对应的材料热物理参数与试验用相变石蜡一致，如表1所示。计算域基础单元尺寸为1 mm，为了准确的描述无滑移边界上的薄边界层，沿壁面法向创建了12层具有密集单元分布的边界层网格，整个计算域内单元数为15 200，节点数为90 009。

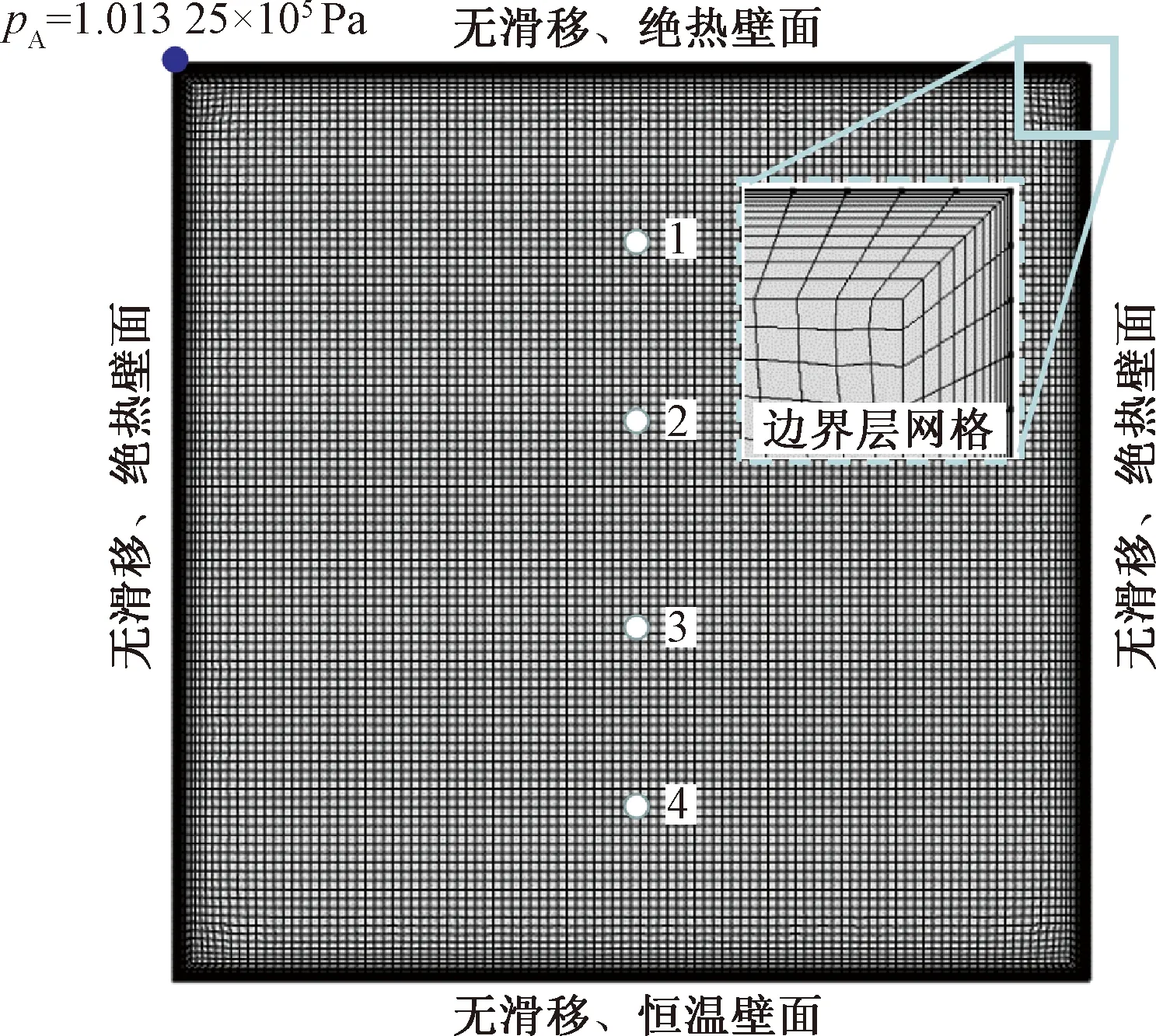
图3 有限元模型Fig.3 Finite element model

有限元模型底边施加Tw=70 ℃的恒定温度热源，其余边界均设置为绝热且无滑移壁面。初始时，相变石蜡的温度T0=16 ℃，液相石蜡在x、y方向的流速分量ux=uy=0 m/s，压强p=1.013 25×105Pa。为了提高计算收敛性，在模型左上角位置施加一恒定点压强约束pA=1.013 25×105Pa。

对相变石蜡熔化储热过程进行计算时，对流项采用二阶迎风格式离散，时间积分采用二阶克兰克-尼科尔森格式。动量方程和连续性方程的求解采用PIMPLE算法，该算法更易于压力和速度的耦合。为了提高收敛性，速度、压力和温度的松弛因子分别设置为0.7、0.3和0.5。

4 结果及分析

4.1 计算模型验证

为了验证图3所示有限元计算模型的正确性，在底部Tw=70 ℃的恒定温度下，分别通过数值计算和试验测试，获取的100 mm方腔内相变石蜡液体分数与熔化时间的关系，如图4所示。

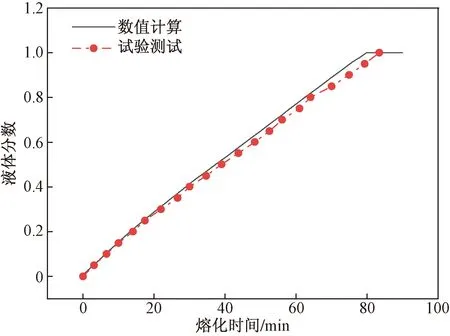
图4 数值计算与试验测试结果对比Fig.4 Comparison between numerical and test results

由图4可知，在熔化蓄热阶段，相变石蜡的液体分数与熔化时间近似呈线性关系。当相变石蜡完成熔化蓄热时，此时液体分数-熔化时间(f-t)曲线发生转折，其中拐点对应的水平时间坐标即为总的熔化时间。基于图3所示计算模型计算的总熔化时间为79.83 min，图1试验测试的总熔化时间为83.43 min，两者相差4.5%。造成试验测试结果偏大的原因为：尽管方腔采用了隔热性能较好的高透明PVC塑料，但腔体外表面与低温环境间的对流换热是不可避免的，存在热量损耗，需要延长加热时间补充腔体边界损耗的热量。此外，数值计算与试验测试结果的较为一致性，表明所建立的方腔内相变石蜡熔化蓄热的流-固-热三场耦合计算模型可用于评估方腔内相变石蜡的熔化蓄热性能。

4.2 自然对流对相变石蜡熔化储热的影响

为了揭示液相自然对流运动对相变石蜡熔化蓄热速率的影响，在底部Tw=70 ℃的恒定温度下，分别计算忽略自然对流和考虑自然对流两种工况下的方腔内相变石蜡液体分数随熔化时间的关系，结果如图5所示。

通过对比熔化前缘形状特征发现，在忽略液相的自然对流传热影响时，熔化前缘始终为水平直线，且与底部恒温热源保持平行。当考虑液相的自然对流传热影响时，熔化前缘为不规则曲线，且不同时刻的曲线形态亦存在显著差异。

通过对比相变石蜡的熔化储热效率发现，在忽略液相的自然对流传热影响时，相变石蜡熔化25%、50%、75%所需的时间依次为157.3、597.5、1 199.2 min；而考虑液相的自然对流传热影响时，相变石蜡熔化25%、50%、75%所需的时间依次为17、37.3、58.3 min；表明液相的自然对流传热效应在相变石蜡熔化储热过程中起着极为明显的促进作用。因此，对相变石蜡的熔化储热性能进行研究时，液相的自然对流运动不可忽略。

4.3 自然对流作用机制

图6为底部Tw=70 ℃的恒定温度下，100 mm方腔内相变石蜡的温度云图及液相自然运动速度矢分布。根据熔化前缘的形态特征及液相流动特征，可将相变石蜡熔化储热的整个过程划分为4个阶段：①热传导阶段；②稳定增长阶段；③过渡阶段；④湍流阶段。

4.3.1 热传导阶段

在相变石蜡熔化储能的初始阶段，熔化前缘始终与底部平行，并垂直向上推进，直至40 s，如图6(a)所示。在该阶，底部热源主要通过热传导的方式向内部传输热量，故称为热传导阶段。热传导阶段液相层的临界厚度不足2 mm。

4.3.2 稳定增长阶段

当熔化储能时间超过40 s后，首先于底部两端边界处出现若干羽流，表示液相层内的自然对流运动开始激活，如图6(b)所示。待熔化至65 s时，液相层内形成了25个连续周期性分布的羽流阵列，且每个羽流两边存在一对稳定的反向旋转的环流，该流动即为经典的瑞利-贝纳特流，如图6(c)所示。在羽流阵列的持续作用下，熔化前缘逐渐由直线转变为波浪曲线，其中单个波长约为4 mm。该典型波浪形熔化前缘特征在相变石蜡熔化试验中也可清晰地观测到，如图2(c)所示。在随后的熔化蓄热过程中，羽流的茎部逐渐变细长，头部变宽，形态逐渐演变为蘑菇状。由于该阶段羽流数目保持不变，且相邻羽流同步垂向生长，称为稳定增长阶段。该阶段持续至150 s，如图6(d)所示。

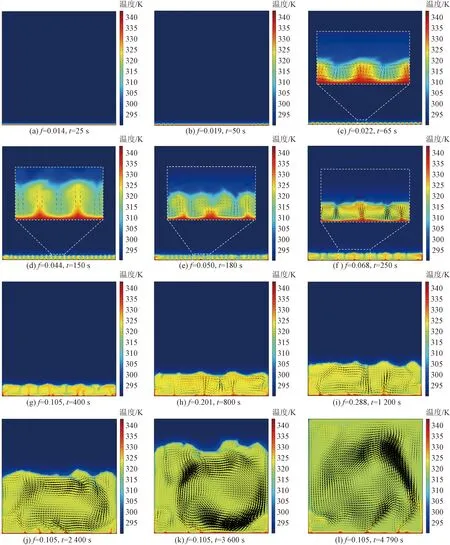
蓝色低温区域(小于300 K)为固体石蜡；黑色箭头表示液相流动的速度矢方向图6 不同时刻的温度场云图及速度矢分布Fig.6 Temperature contours and velocity vector distribution at different time

4.3.3 过渡阶段

随着熔化过程的推进，羽流的茎部开始失去稳定性而产生弯曲，在两侧反向旋转环流的持续作用下一分为二，并分别与相邻羽流融合成较大羽流，如图5(e)～图5(g)。待持续至800 s时，羽流数目由25个减小至3个，对应的熔化前缘失去波浪形特征而变的不规则。该阶段称为过渡阶段。

4.3.4 湍流阶段

当熔化时间超过800 s后，羽流的茎干开始不规律地左右摆动运动，并逐渐失去稳定性而溃灭，进入湍流阶段。该阶段为相变材料熔化蓄热的主要阶段，占总蓄热时间的比例约为83%。该熔化阶段内，在液体石蜡和底部加热区相邻的边界层发生了强烈对流，同时液相中将形成若干大小不等的环流，且环流大小、数目及位置等在随后熔化过程中发生无规律的变化，进而形成不规则的熔化前缘。随着湍流状态的增强，以及羽流的随机生成及不稳定运动，熔化前缘形态产生了更为强烈的变形，如图6(i)～图6(k)。在t=79.83 min时，石蜡融化完毕，完成相变蓄热，如图6(l)所示。

4.4 自然对流的尺寸效应

为了定量标定相变石蜡熔化储热过程中自然对流影响的尺寸效应，在底部Tw=70 ℃的恒定温度下，分别对边长为2、5、10、20、50、75、100 mm的方腔内相变石蜡的熔化蓄热过程进行分析，计算的液体分数与熔化时间的关系，如图7所示。

图7 方腔尺寸对相变石蜡熔化过程的影响Fig.7 Influence of cavity size on melting process of phase change paraffin

由液体分数-时间曲线[图7(a)]的斜率可知，在忽略自然对流传热的影响时，方腔内相变石蜡熔化速率随时间呈持续减小的发展规律，最大蓄热效率发生在熔化初期。对于边长为2、5、10、20、50、75、100 mm方腔内相变石蜡，完成熔化蓄热所需的时间依次为0.82、5.5、20.5、83.5、496.8、1 116.8、2 231 min。进一步分析发现，相变石蜡总熔化时间与方腔尺寸近似呈二次多项式增加关系。

由液体分数-时间曲线[图7(b)]的斜率可知，在考虑自然对流传热的影响时，方腔内相变石蜡的熔化蓄热速率基本为常数。对于边长为2、5、10、20、50、75、100 mm方腔内相变石蜡，完成熔化蓄热所需的时间依次为0.81、2.67、6、14.3、41.2、62.2、79.8 min，即相变石蜡总熔化时间与方腔尺寸近似呈线性增加关系。相对于无对流，相变石蜡熔化蓄热效率依次提升0.01、1.06、2.42、4.84、11.06、16.95、27.9倍。由此可知，液相自然对流传热对相变石蜡的熔化蓄热效率提升存在显著地尺寸效应，当方腔尺寸小于2 mm时，自然对流的提升效率不足1%，此时可忽略不计，如图7(c)所示。

5 结论

针对液相自然对流运动对底边加热下的方腔内相变石蜡熔化蓄热过程，开展理论和试验研究，得出以下结论。

(1)设计并开展底部恒定温度下方腔内相变石蜡熔化蓄热试验，获取相变石蜡熔化蓄热过程中熔化前缘特征演化规律，发现相变石蜡熔化前缘呈现无规则曲线特征。

(2)建立相变石蜡熔化蓄热过程的流-固-热三场耦合计算模型，对比是否考虑自然对流条件下100 mm方腔内相变石蜡熔化过程前缘特征演化规律及熔化蓄热效率发现，液相自然对流传热可使蓄热效率提升27.9倍，且不规则的熔化前缘特征是由液相自然对流造成的。

(3)根据相变石蜡熔化前缘和液相流动特征，可将整个熔化蓄热过程大致可分为四个阶段：热传导阶段、稳定增长阶段、过渡阶段和紊流阶段。其中紊流阶段为相变材料熔化蓄热的主要阶段，占总蓄热时间的比例约为83%。

(4)液相自然对流传热对相变石蜡的熔化蓄热效率提升存在显著地尺寸效应，当方腔尺寸小于2 mm时，自然对流的提升效率不足1%，此时可忽略不计。