基于模糊逻辑系统的采矿船升沉补偿控制方法研究

滕媛媛,陈林恺*,孙友刚,谢颖

(1.上海海事大学物流工程学院，上海 201306；2.同济大学铁道与城市轨道交通研究院，上海 201306；3.上海振华重工(集团)股份有限公司，上海 201306)

深海采矿船在海面上运行的时候由于海浪的涌动会作升沉运动，从而严重影响船体和采矿系统的安全。为保证深海采矿船在进行作业的时候可以安全运行，所以需要对其进行升沉补偿。由于在当前升沉补偿系统一般可以分为被动式、主动式，前者结构简单、补偿精度差，后者结构复杂、耗能高、补偿精度好。周强等[1]通过在绞车型升沉补偿模拟试验台上进行研究；展勇等[2]对半主动升沉补偿系统进行非线性建模与仿真；袁建新[3]对采用液压驱动的主动升沉补偿模型控制研究，为了更好地模拟真实海浪情况，王玉红等[4]对升沉补偿系统实验平台进行设计并展开研究;段玉响[5]对海上吊装主动式升沉补偿与防摆控制系统进行了分析和研究,但是这些学者对于升沉补偿系统的研究大部分是在机械方面的革新，很少有从控制算法的角度进行。控制算法的改善对于机械也可以起到很好的效果。李帆等[6]对桥式起重机的防摇采取模糊比例积分微分(proportion integral derivative，PID)算法进行研究；仝新峰等[7]利用模糊-内模双环控制算法对船岸并网系统进行了分析和研究。基于此，首先分析了当前主流升沉补偿系统的优缺点，并提出了一种结合二者优点的主被动复合式升沉补偿系统，再从控制算法的角度设计模糊控制算法进行控制，最后在Simulink中进行仿真，并将模糊控制算法的仿真结果和传统PID控制算法的仿真结果比较，以验证所提系统和算法的有效性。

1 升沉补偿系统的结构和工作原理

1.1 升沉补偿系统结构

采用的升沉补偿系统是主被动复合式该补偿系统主要的组成部分包含液压站、绞车、液压缸、蓄能器组等，其系统结构简图如图1所示。

图1 主被动复合式升沉补偿系统结构简图Fig.1 Structure diagram of active and passive compound heave compensation system

1.2 升沉补偿液压系统原理

针对被动式补偿系统精度不高、主动式补偿系统能耗过大的缺点，采用主被动复合式升沉补偿系统。在不同工况下可实现被动补偿功能与主动补偿功能的切换，具备更广泛的负载适用性。其液压原理简图如图2所示。

图2 主被动升沉补偿系统液压原理简图Fig.2 Schematic diagram of hydraulic principle of active and passive heave compensation system

被动补偿模式下，比例阀、被动腔充液阀关闭，连通阀打开，主动腔A和B连通，被动腔C与被动腔蓄能器连通，通过蓄能器的柔性吸收升沉运动;一般情况下，被动模式和主动模式是同时工作的，但系统主要是在主动模式下工作。此时连通阀、被动腔充液阀关闭，比例阀根据采集的升沉运动信号闭环控制 补偿液压缸运动，可大幅抵消升沉运动。同时被动腔与蓄能器相连平衡重物重量，可以降低主动控制系统的能耗。

2 采矿船升沉幅值的计算

海浪的激励作用会导致采矿船作升沉、纵摇、进退等六自由度运动，其中升沉运动对采矿船水下系统的安全性影响最大。船舶在海浪作用下升沉方向的动力学响应和船体的重量、外形、尺寸等因素息息相关。船体升沉一般近似为谐波运动，利用采矿船的型号、尺寸、结构及海浪的波长、波高和频率可计算采矿船升沉运动的周期和幅值等参数。假设采矿船的升沉运动为某一简谐运动，则其升沉运动函数为

(1)

式(1)中：ZR为采矿船的升沉位移；ZRS为采矿船的升沉幅值；TH为海浪的波动周期；t为采矿船运动的时间。

根据莫尔经验公式，可以推导出ZRS的计算公式为

(2)

式(2)中：A0,A1，…，A7为随风浪大小和传播尺寸变化的相关系数，需查表2得；CW为水面线系数；CB为方形系数；L为水面线系数；B为船舶宽度；d为船舶的设计吃水深度。

计算采矿船升沉复幅值和周期所需参数如表1所示。

表1 计算采矿船升沉复幅值和周期所需参数Table 1 Parameters required to calculate the recovery amplitude and period of the mining ship heave

A0,A1,…,A7为相关系数，取决于风级和船的体积，其取值如表2所示。

表2 相关系数的插值结果Table 2 Interpolation results of correlation coefficients

经计算，得出在波高为±2.5 m、周期为5.8 s的海况下，采矿船的升沉幅值为0.36 m，周期为5.8 s。

3 升沉补偿系统数学模型的建立

升沉补偿系统的组成部分包括比例阀、复合液压缸、活塞式蓄能器等。因此要对其各组成部分的模型进行数学建模，并且推导出中间传递函数，最后才可以推导出总传递函数。

3.1 比例阀模型

由于比例阀的组成环节比较多，因此很难知道各种参数并建立一个精确的数学模型。在实际应用中，需将阀芯运动简化为一阶系统，其传递函数为

(3)

式(3)中：TXU为阀芯运动的时间常数；KXU为阀芯位移-电压增益系数。

3.2 复合液压缸模型

沉补偿系统采用复合式液压缸结构，如图3所示。采用复合式的设计，把主动油缸和被动油缸集成在一起，在实现主动被一体化的同时大大节约了装备空间。

图3 复合式液压缸结构示意图Fig.3 Schematic diagram of compound hydraulic cylinder structure

根据牛顿第二定律，钢丝绳拉力与重物受力平衡方程为

(4)

式(4)中：Fm1为钢丝绳拉力；G为采矿船重力；Fb为负载浮力；XL为负载位移。

在主动升沉补偿作用下，液压缸受力平衡方程为

(5)

式(5)中：Ac为液压缸被动腔C腔作用面积；pc为蓄能器液压力；Ap为液压缸主动腔A、B腔的作用面积，Ap=Aa=Ab;pL为系统压力；Mt为液压缸缸杆处的等效质量；xp为补偿液压缸位移；Bp为黏性阻尼系数；K为液压缸缸杆处的等效负载刚度。

液压缸主动补偿腔流量连续性方程为

(6)

式(6)中：qL为液压缸负载流量；Vt为液压缸作用有效体积；Ctp为液压缸总泄漏系数；βe为有效体积弹性模量。

3.3 活塞式蓄能器模型

活塞式蓄能器采用浮动活塞将液体与气体隔离，并和气瓶组合使用。在大流量、大体积的工况下可以保证液压油输出压力的相对稳定。

活塞式蓄能器活塞受力平衡方程为

式(7)中：pg为气体压力；Ag为活塞蓄能器活塞作用面积；m为活塞质量；Bg为等效黏性阻尼系数；Kg为等效刚度系数；xg为活塞蓄能器活塞位移；Ffg为活塞摩擦力。

3.4 半主动模式下主动补偿系统模型

液压缸主动补偿腔流量连续性方程为

(8)

在升沉补偿作用下，液压缸受力平衡方程为

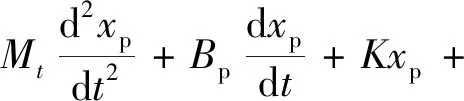
(9)

式(9)中：FZZ为垂直方向上的流体惯性力。

因此，半主动补偿模式下,比例阀阀芯位移产生的液压缸缸杆位移传递函数为

(10)

式(10)中：Kce为总泄露系数；Xsv为比例阀阀芯位移。

4 主动升沉补偿控制器设计

在半主动升沉补偿模式下，需要针对主动式补偿工作模式，设计基于模糊逻辑系统的PID控制器。

模糊逻辑控制方法适用于相对复杂且目前无法得到精确模型的控制系统中，可以提高系统的控精度，故该方法目前使用较为广泛。针对升沉补偿系统的参数不确定性、非线性强、有滞后的特点，用模糊逻辑系统可实现无模型下的控制器设计以提高主动补偿系统的鲁棒性。模糊逻辑系统的设计过程如图4所示[8]。

图4 模糊算法设计的步骤流程图Fig.4 Flowchart of fuzzy algorithm design

根据采矿船作业特点和控制经验，所提出的模糊规则如表3所示。建立模糊控制规则其实就是将控制经验通过模糊语言描述出来[9]。常用的模糊控制器形式有Mamdani型和T-S型。相比于T-S模糊逻辑系统，Mamdani型模糊规则输出为模糊量，与人类的自然语言信息相似，易于理解，因此选择Mamdani型控制器[10]。

表3 模糊规则Table 3 Fuzzy rules

基于模糊逻辑系统的PID 控制器的设计过程如下：首先定义e为实际位移和期望位移的差值，ec为实际位移和期望位移的差值随着时间变化的变化率。再通过传感器对e与ec的变化率 进行检测，然后通过量化因子Ke与Kec将其转化到模糊论域中，从而得到要PID控制器3个参数的增量ΔKp、ΔKi、ΔKd[11]。

模糊控制器的一般原理表达式为

(11)

式(11)中：Kp为模糊控制器的比例控制参数；Ki为模糊控制器的积分控制参数；Kd为模糊控制器的微分控制参数。

最后对3个参数进行计算,得到最终输入PID控制器的参数，可表示为

(12)

代入式(9)，得到本升沉补偿模糊控制器的设计的最终表达式为

(13)

式(13)中，Kp0为初始时刻的Kp值；ΔKp为Kp值的变化量；Ki0为初始时刻的Ki值；ΔKi为Ki值的变化量；Kd0为初始时刻的Kd值；ΔKd为Kd值的变化量。

结合本升沉补偿系统实例，可得到图5所示的3D可视化模糊规则，更直观地看出Kp、Ki、Kd随着e和ec的变化而变化的情况[12]。

图5 Kp、Ki、Kd的可视化模糊规则示意图Fig.5 Schematic diagram of visual fuzzy rules for Kp、Ki、Kd

5 仿真结果

模型搭建完需进行仿真，所提升沉补偿系统的仿真参数如表4所示[13]。

表4 半主动式升沉补偿系统仿真参数Table 4 Simulation parameters of semi-active heave compensation system

图6 采矿船的实际升沉位移曲线Fig.6 Actual heave displacement curve of mining ship

在规则海浪波下，利用模糊控制对升沉补偿系统对主动补偿模式进行控制，模糊控制算法中，先设定一个PID参数的预设值和误差范围，PID参数可以实时变化，起到自动调节PID参数的作用[15]。PID参数分别预设为150、50 10，仿真时间为50 s。模糊控制中PID参数变化过程示意图如图7所示，其中图7(a)、图7(b)为规则海浪波下PID参数变化，图7(c)为不规则海浪波下PID参数变化[16]。二者的仿真结果曲线示意图如图8所示。

图7 模糊控制算法下Kp、Ki、Kd值变化过程Fig.7 Value change diagram fuzzy control algorithm forKp，Ki，Kd

图8 模糊控制和传统PID控制算法下仿真结果对比Fig.8 Comparison of simulation curves between fuzzy control and traditional PID control algorithm

把数据导出进行计算，可知其补偿精度结果如表5所示。

表5 升沉补偿系统仿真结果精度结果Table 5 Precision results of heave compensation system simulation results

从表5可以看出，模糊控制算法的精度要优于传统PID控制算法的精度，尤其是在不规则海浪波下，模糊控制算法的优势更能被体现。

6 结论

针对采矿船升沉运动引起的纵向动力响应问题，提出了一种主被动复合式的升沉补偿系统。并从控制算法的角度对其进行分析，设计了模糊控制算法，在Simulink中分规则海浪波和不规则海浪波下进行仿真和比较，同时把模糊控制算法的仿真结果和传统PID控制的算法仿真结果进行比较，得出以下结论。

(1)在规则海浪波下，传统PID控制的补偿精度在为90.4%；模糊PID控制的补偿精度为93.2%，模糊控制补偿精度比传统PID控制的补偿精度高3.2%。

(2)在不规则海浪波下,传统PID控制的补偿精度在为91.5%；模糊PID控制的补偿精度为98.2%，模糊控制补偿精度比传统PID控制的补偿精度高7.1%。

(3)模糊控制算法的精度优于比传统PID控制算法的精度，尤其在不规则波下，更能体现模糊控制算法的优势。