基于互补滤波算法的倾斜RTK姿态解算
刘坤之,唐诗华*,张炎,李灏杨,吕富强
(1.桂林理工大学测绘地理信息学院,桂林 541004;2.广西空间信息与测绘重点实验室,桂林 541004)
RTK(real time kinematic)是一种利用GPS载波相位观测值进行实时动态相对定位的技术,可以实时提供指定坐标系下观测点的三维坐标。倾斜RTK是通过内置惯性测量单元(inertial measurement unit,IMU),根据内部惯性器件计算的姿态角生成方向余弦矩阵,从而实现空间矢量的坐标转换,将天线相位中心位置补偿到地面测量点,得到待测点坐标。解决了传统RTK测量过程中在特殊作业情况下不能保持对中杆竖直,出现定位误差较大的问题。
惯性测量器件具有体积小、成本低、重量轻和精度高等优点,适用于倾斜RTK的姿态检测。但是在运动过程中,微机电系统(micro electro mechanical system,MEMS)惯性传感器,无法实时的获取准确的姿态信息,导致解算出的姿态精度较差,无法直接使用。通过利用不同传感器的自身特性,文献[1]提出了一种基于加速度修正模型的姿态解算法,搭建卡尔曼滤波算法,减弱非重力加速度对姿态解算的干扰,提高了姿态解算的精度和抗干扰能力。文献[2]利用混合滤波的算法对加速度计和磁力计数据进行四元数的最优估计,通过设计自适应滤波器调参,有效的降低磁干扰,减少加速度对姿态解算的影响。文献[3]采用一种自适应增益互补滤波算法,融合九轴传感器数据,设计互补卡尔曼滤波器,实现姿态估计,但该算法计算量较大且容易产生奇异值。文献[4]设计一种自适应无迹卡尔曼滤波算法,基本消除了噪声干扰和信号野点值,有效的抑制了陀螺仪漂移引起的姿态角发散问题。文献[5]对粒子滤波的重采样过程进行了改进,应用拓展卡尔曼滤波(extended Kalman filter,EKF)对系统状态预测,根据不同环境自适应调参,优于传统的粒子滤波算法,但计算量太大,实时性仍有不足。因此,设计了一种基于互补滤波的融合算法,设置PI控制器,用DE算法对参数寻优,实时解算出最优姿态角。通过惯导模块搭载全站仪实时采集数据,对本算法进行仿真验证,为倾斜RTK确定姿态提供一种可行方案。
1 基于互补滤波的姿态解算原理
1.1 空间姿态描述
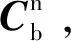
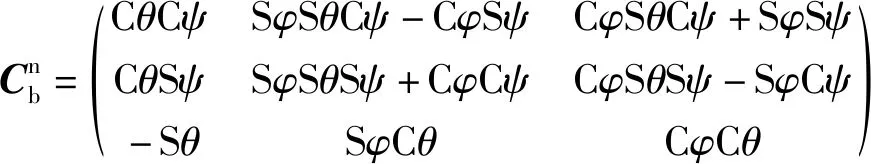
(1)
式(1)中:φ为横滚角;θ为俯仰角;ψ为航向角;C表示cos;S表示sin。
欧拉角在空间姿态的描述是非常直观理解的,但是存在的问题也很严重。函数的自变量和因变量是相同的,无法直接求解;含有大量的三角运算,会拖慢主控芯片的运行效率;存有万向节死锁等问题。因此,需要一种方便计算的描述方式——四元数。
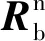
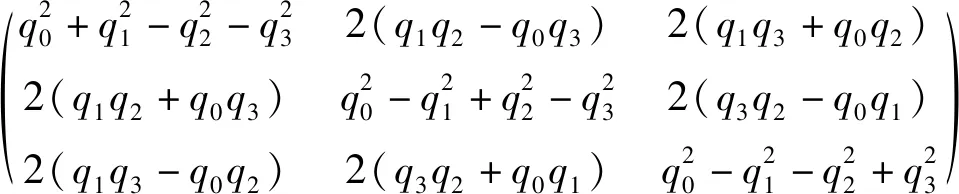
(2)

(3)
θ=arcsin2(q0q2-q1q3)
(4)
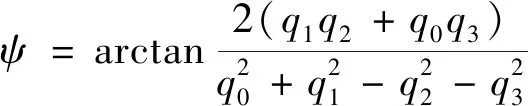
(5)
式中:q0、q1、q2、q3为四元数的基本元素。
1.2 四元数姿态求解
传感器姿态的变化即为四元数的变化,需要构建四元数关于时间的微分方程研究此类问题。由于计算机中的计算是离散的,需要采用一阶龙格库塔法对微分方程离散化处理[7],从而实现四元数的更新计算。计算公式为
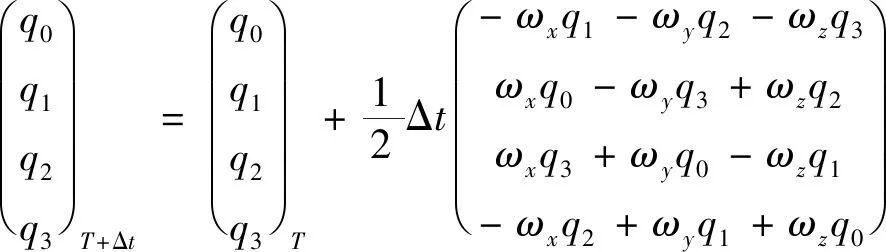
(6)
式(6)中:ωx、ωy、ωz分别为陀螺仪输出的x、y、z轴角速度;T为时刻;Δt为数据更新的频率。
1.3 传感器数据融合
六轴传感器有两种计算角度的方法:一是对角速度直接积分得到角度,如果角速度积分时在某个瞬间引入误差,随着积分的过程,误差将会一直累加,形成低频误差;二是对加速度正交分解计算角度,由于加速度计是比较敏感的传感器,载体在运动的过程中,微小的运动都将会对加速度的数据造成影响,产生高频误差[8]。可以将两种传感器融合起来,利用一种向量外积补偿的互补滤波算法,更新四元数,解决上述问题,如图1所示。
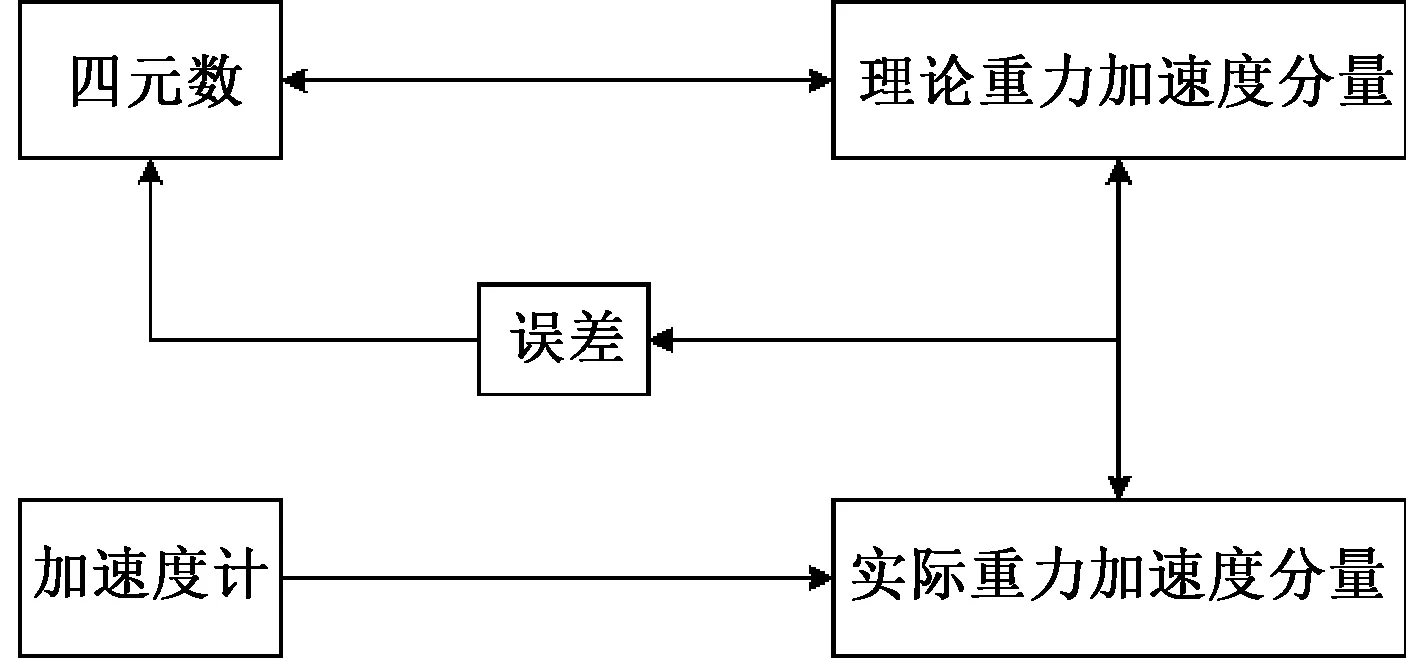
图1 误差补偿原理图Fig.1 Schematic diagram of error compensation
四元数和理论上的重力加速度分量,是可以相互推导,具体的变换关系式为


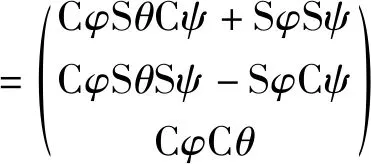

(7)
式(7)中:vb为理论重力加速度;vbx、vby、vbz为b系下x、y、z轴理论重力加速度;gn为n系实际重力加速度。
加速度计实测重力加速度与理论重力加速度二者之间出现的偏差,很大程度是因为陀螺仪数据产生的角速度误差引起的,产生的偏差可以通过向量外积补偿解算陀螺仪数据的误差[9],可表示为
|ρ|=|gb||vb|sinα
(8)
式(8)中:ρ为外积向量;α为向量夹角;gb为b系实际重力加速度。
叉乘运算前对理论向量和实际向量归一化处理,且由于载体瞬时运行角度不会超过45°,可以对sinα小角近似处理,可表示为
|ρ|≈α=error
(9)
式(9)中:error为误差补偿值,该补偿值不能直接应用到陀螺仪的数据中,因此构建比例积分补偿器来控制补偿值的大小和精度。控制器表达式为
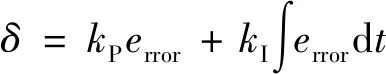
(10)
式(10)中:δ为陀螺仪误差补偿量;kP为比例控制项;kI为积分控制项;dt为对时间的积分。
补偿量加到角速度上后,即可得到可信度较高的陀螺仪数据,将所求陀螺仪补偿量代入式(6)更新陀螺仪数据即可得到当前四元数。
2 基于DE算法的PI控制参数寻优
加速度计测量的是物体在外力影响下造成的一种微小形变,在静止不动时Z轴输出的是1g(g为重力加速度)的加速度,但是传感器在三维运动时,它不能分辨重力加速度和外力加速度,因此,计算的误差补偿不能全部用于更正角速度。PI参数作为控制系统精度的主要参数之一,其比例项kP用于控制传感器的“可信度”,积分项kI用于消除静态误差,为满足快速性和精确性的要求,对其参数整定至关重要。传统PI参数整定一般选择手动调参,存在工作量大、效率低和参数不满足要求等缺点。利用差分进化(differential evolution,DE)算法对PI参数进行参数整定,可以快速寻找满足要求的参数,提高系统的控制精度和鲁棒性。
2.1 DE算法基本原理
差分进化算法是基于现代智能理论的自适应全局优化算法,与其他基于群体的进化算法相比,它是以达尔文生物进化论“优胜劣汰,适者生存”的理论为原则,模拟生物界生物进化的群体差异的启发式随机搜索算法[10]。DE算法寻优过程分为:①种群初始化;②通过差分策略实现个体变异;③以概率的形式交叉操作随机生成新的个体;④采用贪婪选择的策略选择较优的个体作为新的个体。
对于无约束优化问题f(Xi)min,Xi=[xi,1,xi,2,…,xi,D]为问题的解,D为优化的维度,i=1,2,…,n,DE算法的实现步骤如下。
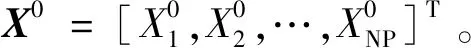
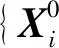
j=1,2,…,D}
(11)

(12)

步骤2实现个体变异。设迭代次数为G,在第g代迭代中,随即从群里中选取一定数量的个体,把所选个体作为目标变量进行矢量变异,同时为了加强DE算法的搜索能力,避免陷入局部最优解,对搜索步长的控制参数缩放变异因子合理取值,更新传统的差分进化算法,其表达式为

(13)
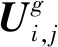
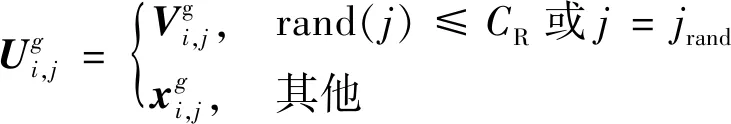
(14)
步骤4选择操作。将父代个体与子代个体的一一对应选择,选取适应度值较小的个体进行下一代搜索,组成新一代种群,实现选择操作,其表达式为
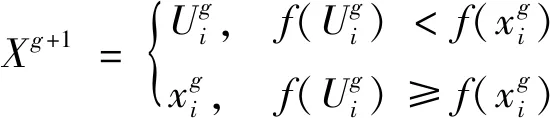
(15)
通过不断重复进行式(12)~式(15)操作,直至满足条件终止,方可得出最优参数估值。
2.2 适应度函数选取
PI参数是PI控制器中重要的影响因子,DE算法是对PI控制器的参数进行合理选取,实现最优解的工作。核心是根据目标函数构建合适的适值函数,通过选取合适的光滑因子求出最佳的目标值,可将目标值与参考值比较得到的均方根误差(root mean square error,RMSE)作为目标函数和评价指标,当均方根误差值最小时,说明所求目标值达到最优效果,所选的光滑因子为最佳[13]。目标函数RMSE表达式为
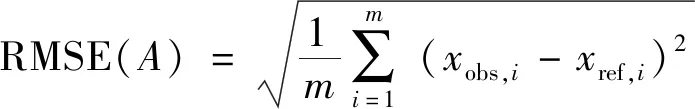
(16)
式(16)中:A为姿态角;xobs为解算的姿态角;xref为参考姿态角;m为采样点数。
考虑DE算法的适应度值越小越好的要求,仿真倾斜RTK工作时对中杆倾斜对载体姿态的影响,为满足瞬态响应振荡小,具备快速性和稳定性的性能,选用均方根误差作为DE算法的适应度函数。根据上诉步骤编写DE算法,建立优化算法与联合仿真模型的数据交互,修改PI控制器中的不确定参数,得到姿态解算的最优值。完整的流程图如图2所示。
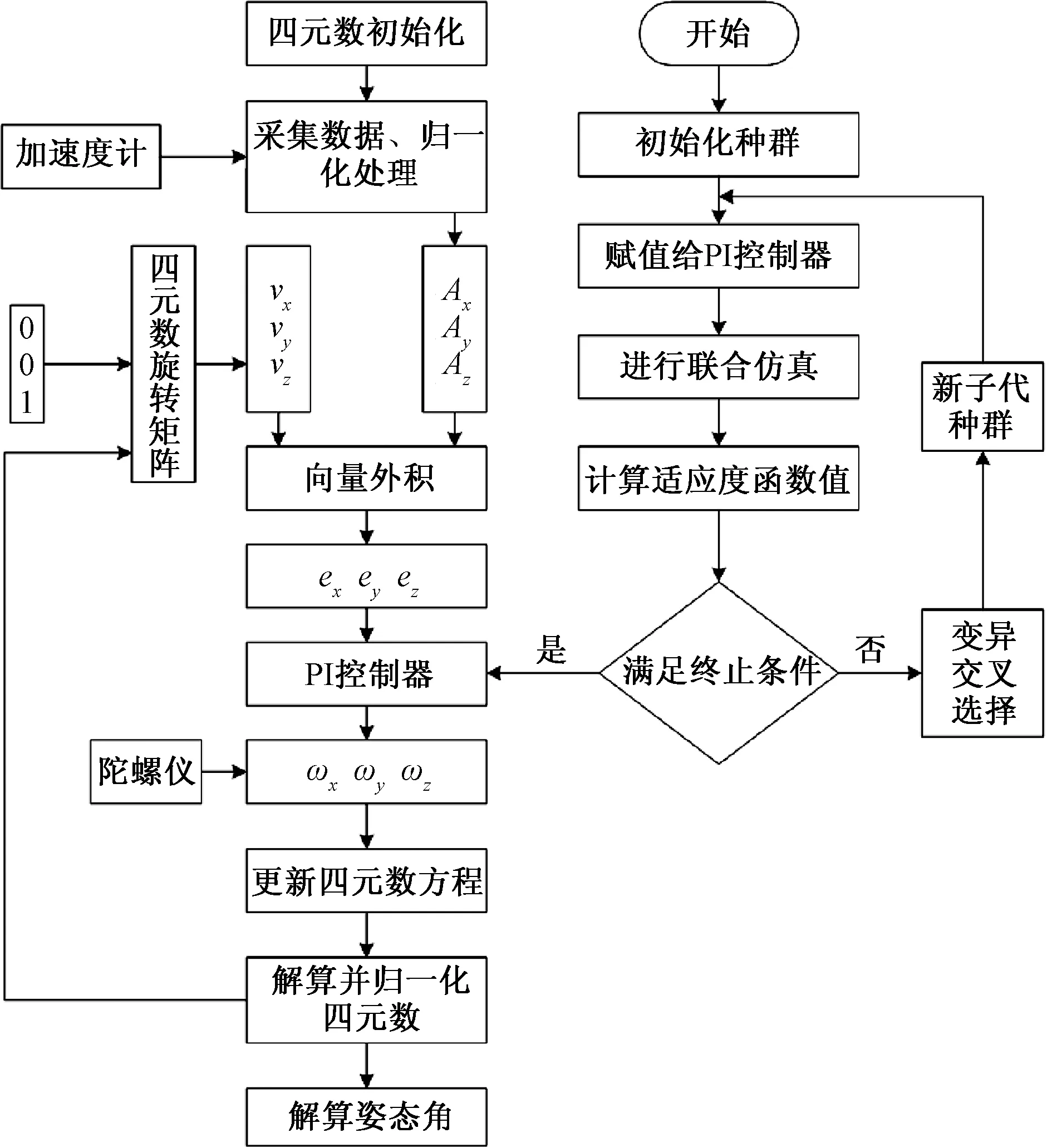
vx、vy、vx为x、y、z轴理论重力加速度;Ax、Ay、Az为x、y、z轴实际重力加速度;ex、ey、ez为三轴外积误差图2 处理流程图Fig.2 Processing flow chart
为了验证DE算法对PI参数模型整定的优越性,同时使用粒子群优化(particle swarm optimization,PSO)算法对适应度函数进行仿真对比分析。各优化算法中控制参数的选择会直接影响算法快速准确运行的结果,DE算法有3个基本控制参数:种群大小NP取20;缩放因子F取0.4~1;交叉概率常数CR取0.5~1;kP取值范围为1~7;kI取值范围为0.01~0.8。PSO基本参数与DE算法一致。两个算法经过50次迭代进化后目标函数值的变化如图3所示,两种算法计算的最优函数值均为0.388 78,DE算法在迭代第7次便得到函数最优解,PSO算法在第32次才得到,对比分析可得DE算法比较稳定,收敛速度较快;是一种概率性全局寻优算法,不容易陷入局部最优解;具有较强的环境交互能力;可进行大规模并行性运算。由此可见使用DE算法对PI控制参数整定,提高系统的鲁棒性与收敛速度具有明显的优势。
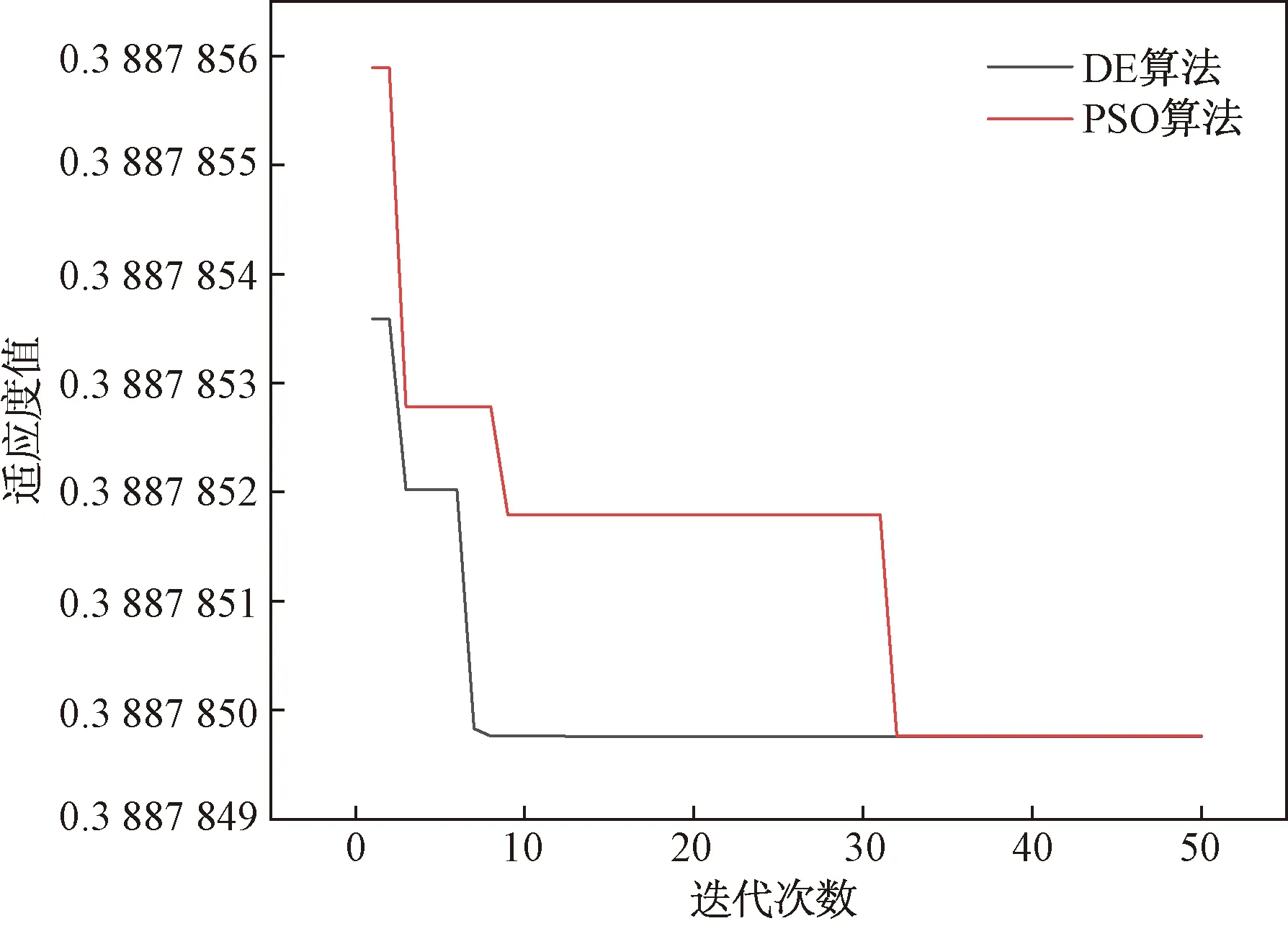
图3 适应度函数值Fig.3 Fitness function value
3 实验验证及结果分析
图4为惯导模块搭载SOUTH全站仪(NTS-362L)作为实验平台模拟倾斜RTK的工作环境,该惯导模块具有稳定的角度输出,均方根(root mean square,RMS)作为传感器的精度的评定标准,其中航向角0.5°RMS,横滚与俯仰静态0.05°RMS,动态0.1°RMS,根据协议要求使用50 Hz的IMU数据输出频率,波特率为921 600,加速度计量程为±16g,分辨率为0.5 mg,零偏稳定性为0.04 mg,陀螺仪量程为±2 000(°)/s,零偏稳定性为10(°)/h,分辨率为0.02(°)/s。为验证算法的可行性和有效性,通过上位机对3轴加速度计,3轴陀螺仪进行原始数据的读取,将模块输出姿态角作为参考对比对象,使用MATALB对融合算法仿真实验,其中基于差分进化的互补滤波算法(DE-mahony)为智能寻参,传统的mahony互补滤波算法为手动调参。将DE-mahony与mahony互补滤波算法和拓展卡尔曼滤波算法进行动态和静态两部分姿态解算结果对比分析。

图4 模块搭载平台Fig.4 Module carrying platform
3.1 静态对比实验
通过全站仪气泡居中的方法将模块水平安装放置,利用模块内置安装角误差矫正功能补偿校准,则系统输出的俯仰角和横滚角的参考值均为0°,航向角在系统初始时刻参考值也为0°。在静止状态下,图5为3种算法的三轴姿态解算对比结果,mahony算法解算姿态角在参考角度附近上下浮动,相较于EKF算法稍稳定些;EKF算法解算姿态角浮动较大,稳定性较差,过程噪声影响较大;DE-mahony算法解算姿态角在参考角度和0°附近浮动,浮动范围小,相对较稳定。

图5 静态三轴角度Fig.5 Static triaxial angle
为了更直观的比较3种算法的解算精度,静态情况下使用均值比较法对比分析估算精度,结果如表1所示。可以看出,使用所提出的DE-mahony算法的解算的三轴精度优于mahony算法和拓展卡尔曼滤波算法;DE-mahony解算的横滚角均值为-0.004 6°,与其他两种算法相比分别降低了36.1%,33.3%;俯仰角均值为-0.000 71°,与其他两种算法相比较降低了94.6%,4.1%;航向角均值为0.024 5°,与其他两种算法相比降低22.7%,18.6%。3种算法解算的三轴静态姿态角度精度均小于0.1°,可以满足倾斜RTK日常工作需求。
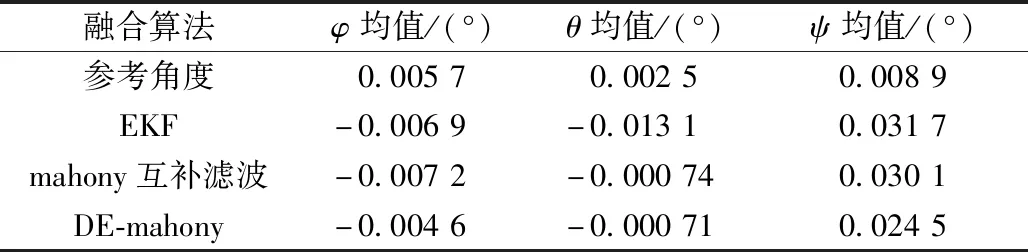
表1 静态解算结果Table 1 Static solution results
3.2 动态对比试验
倾斜RTK的工作环境中,横滚角与俯仰角的倾角需小于60°才能保证解算坐标的精度,仿真实验时以模块输出角度作为参考角度,将模块在平台上60°以内无规则转动约100 s,图6为动态三轴姿态解算对比结果,从波形上可以看出,3种算法与参考姿态角基本吻合,通过放大图对比分析可得,EKF与mahony互补滤波误差相差不大,DE-mahony算法则震荡明显减小,收敛速度更快,更靠近参考角度曲线。由于采用六轴解算,仅使用加速度计修正陀螺仪,航向角在重力方向无修正作用。在角度递增或递减时误差较小,而转折时陀螺仪引入积分误差,且随着时间的推移,陀螺仪积分漂移现象严重,最终会导致航向角出现较大误差。
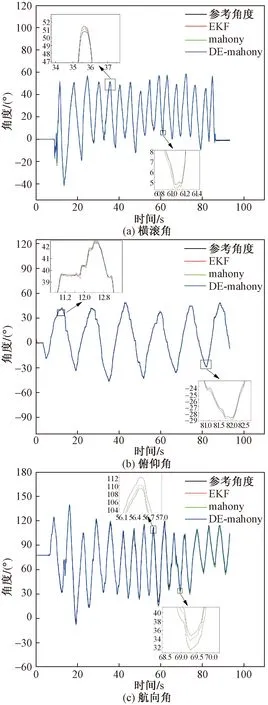
图6 动态三轴角度Fig.6 Dynamic triaxial angle
动态情况下使用中误差作为算法性能的评价标准,由表2对比分析可知,3种算法的精度,DE-mahony解算的横滚角均方根误差为0.430 8°,相比于传统mahony互补滤波和EKF分别降低了28.7%和24.5%;DE-mahony解算的俯仰角均方根误差为0.391 2°,相比于传统mahony互补滤波和EKF分别降低了15.6%,10.4%;mahony解算的航向角均方根误差为1.597 9°,相比于传统mahony互补滤波和EKF分别降低了17.8%,21.5%。动态结果分析中三轴横滚角与俯仰角解算精度较高,误差范围在0.4°~0.6°;航向角由于陀螺仪累计误差,精度较差,误差范围在1.5°~2°。
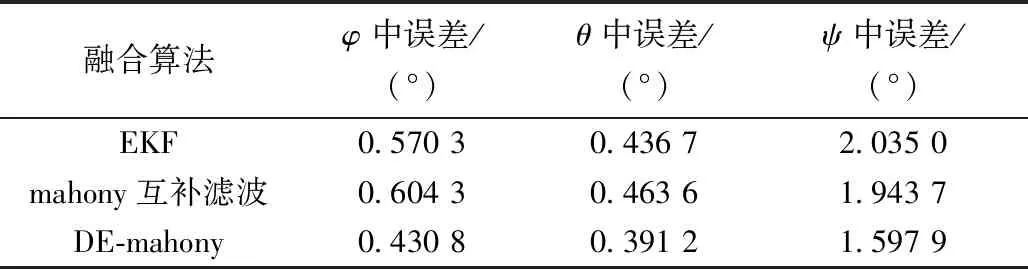
表2 动态解算结果Table 2 Dynamic solution results
4 结论
针对低成本六轴惯性传感器解算姿态的问题,提出了一种基于差分进化智能寻参的互补滤波算法,将惯导模块中的加速度计与陀螺仪利用PI补偿器进行信息融合,通过四元数计算出3个姿态角的变化,为倾斜RTK复杂环境的运动提供状态信息。得出如下结论。
(1)在静态测试中,3个姿态角的精度可以控制在0.1°以内,相比于EKF与传统的mahony互补滤波,所提算法稳定性能更好,鲁棒性更强。
(2)在动态测试中,3种算法均是利用陀螺仪动态性能好但随时间会有积分漂移的特点,使用加速度计对陀螺仪进行实时修正,所提算法所得横滚角与俯仰角中误差在0.5°以内精度优于EKF与传统mahony互补滤波;由于加速度计对航向角没有修正作用,航向角会随时间积分导致误差累计,误差在1.6°,相较于EKF与传统mahony互补滤波精度提高了17.8%和21.5%。
该六轴姿态解算算法不但可以避开万向锁死结的问题,而且对数据的融合补偿达到最大化的利用,同时相比拓展卡尔曼滤波具有较小的计算量,表现的精度效果更好,可以满足倾斜RTK功能的使用。而针对加速度计和陀螺仪的高低频特征需对其滤波处理,以及使用磁力计矫正航向角误差和抗磁干扰内容,将在后续的研究中进一步改进。

