离散重复控制系统设计:一种幂次吸引律方法①
孙明轩 王 晗 邹胜祥
(浙江工业大学信息工程学院 杭州310023)
0 引言
滑模控制能够有效处理受控系统动态结构和参数不确定性,是实际工业过程中常常采用的控制技术。控制设计能够使得切换变量有限时间到达设计的滑模面,并将其维持在滑动面上,具有滑模不变性。等效控制方法与趋近律方法已经发展成为滑模控制系统设计的主流方法[1]。等效控制使得系统瞬时达到切换面;趋近律即等式形式的达到条件,规定了系统趋近切换面的吸引过程。文献[2]中给出了两种典型的趋近律:切换型趋近律和幂次趋近律。为了实现有限时间控制性能,需滑动模态具有限时间收敛性能,通常采用终态滑模控制方法[3-4]。在连续有限时间系统中,除了切换律外,幂次律引起了大量关注[5-7]。其收敛时间与初态有关,初态离原点越远,收敛时间越长。双幂次律能够实现固定时间收敛,收敛时间不取决于初态[8]。其中关于收敛时间的估计采用了两段分析法,这种分析法在文献[9,10]中也有过报道。除了给出收敛时间表达式或对其估计外,人们还注重给出稳态误差界的估计,特别是针对幂次趋近律[11-15],文献[12,13]利用双幂次趋近律提高趋近速度。文献[14,15]提出多幂次趋近律,较传统幂次趋近律具有更好的运动品质。
由于计算机技术在控制系统实现方面的广泛应用,研究离散控制系统综合方法是十分重要的。文献[16]中采用的离散趋近律能够削弱颤振现象,但趋近律形式上看是时间依赖的。文献[17,18]将切换趋近律中的符号函数替换为连续的饱和函数,使得控制量连续化,从而削弱抖振的影响。文献[19]给出了进入稳态误差带所需步数的估计。针对幂次趋近律,文献[20]分析了不同参数选取下的系统平衡点和极限环的稳定性,文献[21]证明了稳态误差带为O(T2) 数量级,这里T为采样周期,文献[22]提供了稳态误差带估计的具体表达式。文献[23,24]通过修正幂次函数,保证切换函数单调收敛,即无正负交替地快速趋近于零,改善了原趋近律中断续函数可能导致的抖振问题。文献[25]将幂次与等速趋近律相结合,采用的混合趋近律进一步减小了滑模面趋近时间。
常规的滑模控制策略并未保证跟踪误差有限时间收敛,这是提出终态滑模控制的主要原因。为了实现跟踪误差有限时间收敛,文献[26,27]提出了一种适用于离散控制系统的吸引律方法。常规的极点配置方法用于线性控制系统设计,闭环性能的改善是通过改变闭环极点位置实现的,能够实现指数吸引性能。相较于极点配置方法,吸引律方法是非线性系统方法,旨在改进控制过程的收敛性能;吸引律的作用可类比于极点配置方法中的期望多项式,可以取作渐稳、指数稳定或有限时间稳定的非线性系统。与吸引律方法相联系的是趋近律方法[28]。传统滑模控制实现闭环系统有限时间控制性能需要两步:有限时间趋近及有限时间滑模;趋近律用来确定滑模控制中的切换变量关于切换面的趋近过程。吸引律代表了期望误差动态,是对跟踪误差本身趋于零的吸引过程的规定,控制器设计无需定义切换函数、切换面,控制过程无趋近过程,不存在滑动模态。它之所以能够改进收敛时间以及各性能指标,实际上是将切换面换成了原点,将关于滑模的不变性换成了关于原点的不变性。吸引律方法设计的闭环系统同样具有关于参数漂移和外部干扰的鲁棒性能,不同之处在于滑模控制考虑滑动模态的不变性,而吸引律方法注重稳态过程的不变性。因而,吸引律方法可以被看做是一种“全局滑模”方法。
针对不确定系统,基于常规吸引律设计的控制器存在不确定项,在实际中无法实现,因此需要采用理想切换动态方法[26]。为了刻画控制性能,文献[26]推导出了误差动态的稳态误差带,绝对吸引层和单调递减域。进一步地,将干扰差分补偿抑制措施“嵌入”吸引律,构建理想误差动态,干扰差分有效地抑制了干扰的影响[29]。工业应用场合存在大量执行周期跟踪任务的系统、过程与装备,重复控制是这类受控对象的一种适用的控制技术[30],同样可实现关于周期性扰动信号的完全抑制。文献[28,31]提供了一种简便的离散滑模重复控制器设计方法。
有限时间控制已经发展成为一种有效的控制策略,而构造新型吸引律,进一步丰富吸引律形式,并分析干扰性存在时相应的收敛性能已成为值得研究的方向。典型的吸引律形式分切换型和非切换型,幂次吸引律属非切换型,是一种基本形式。目前已发表结果集中于切换型,涉及幂次形式的收敛特性分析的不多;特别是已发表结果多集中于调节时间的推导,较少分析幂次取值对收敛过程的影响。
本文研究幂次吸引离散重复控制方法,实现对周期干扰完全抑制的同时,为了抑制扰动中存在的非周期成分,借助于扩张状态观测方法[32],设计扰动观测器,以便补偿干扰非周期性成分,进一步提高控制性能。为了刻画闭环系统的吸引过程和稳态性能,本文给出稳态误差带、绝对吸引层和误差收敛稳态误差带的最大步数的具体表达式。特别地,为了方便实现,对幂次选取进行了讨论。本文给出幂次吸引律各性能指标的一般形式求解表达式(未指定幂次),以方便数值求解;并讨论了具体幂次取值的情形,给出各个指标的解析表达式。具体幂次与一般幂次的结果能够为实现适时的参数整定提供依据。
1 问题的提出
考虑如下单输入单输出离散时间系统

式中,uk为控制输入;yk为系统输出;wk为干扰信号;A(q-1)和B(q-1) 为延迟算子q-1的多项式,A(q-1)=1+a1q-1+…+anq-n,B(q-1)=b1q-1+…+bmq-m,其中a1、…、an,b1、…、bm为系统参数,且b1≠0,1 ≤m≤n。
给定的参考信号rk是周期的,满足rk=rk-N,N为该参考信号的周期。本文讨论适用于系统式(1)的、实现周期参考信号跟踪的重复控制问题,控制目标是采用吸引律方法设计控制信号uk,使系统式(1)的实际输出yk在有限时间内跟踪上给定的周期参考信号rk,且能够精确刻画吸引过程。记跟踪误差ek=rk -yk,控制目标可以描述为:通过重复控制使跟踪误差有限时间收敛于原点的尽可能小的邻域内。
采用吸引律方法设计重复控制器,旨在预先能够规定闭环系统跟踪误差瞬态稳态性能。文中提出了一种离散幂次吸引律,并给出其吸引域ΔAB。采用3 项性能指标对离散幂次吸引律的吸引过程进行刻画,包括绝对吸引层ΔAA、稳态误差带ΔSS以及跟踪误差首次进入稳态误差带的最大收敛步数,具体定义见文献[27,29]。进一步地,分析各参数取值(特别是幂次α)对给出的吸引指标的影响,为具体实现时的参数整定提供依据。
为达到上述重复控制目标,文中对原有吸引律形式进行修改,设计重复控制方案,使得闭环系统中周期干扰信号能够完全补偿;同时,借助于扩张状态观测器方法,在控制方案中引入干扰估计补偿,对非周期干扰信号进行有效抑制。
2 幂次吸引律方法
按照吸引律方法设计离散重复控制器,需事先指定离散吸引律的具体形式。离散吸引律的获得途径有两种。一种是直接构造离散吸引律;另一种采用离散近似方法,先给定连续吸引律,经由离散化,获得离散吸引律。本文考虑下述离散幂次吸引律:

采用重复控制器式(4),闭环系统的误差动态由式(3)所规定。因此,可以对闭环系统跟踪误差的吸引性能进行刻画,为实现时的参数整定提供参考。从上述重复控制器推导过程可以看出,其并未定义切换函数,提出的吸引律方法与文献[24,28,31]中的滑模重复控制设计方法是不同的。与文献[26,27]中采用的切换吸引律不同,本文采用了幂次吸引律,并给出这一基本吸引律的收敛性能。
式(4)中,需设计观测器对等效扰动dk进行估计,并以观测值补偿等效扰动的影响。借助于扩张状态观测器方法[32],采用如下形式的观测器:

3 吸引域
连续幂次吸引律中的ρ只要大于0 即可,即全局吸引,且ρ的取值越大,收敛速度越快。然而,对于离散吸引律,却存在一个吸引域,其边界记为ΔAB时,当跟踪误差满足| ek| >ΔAB时,该闭环系统的误差动态是吸引的。实际上,由压缩条件可知,离散吸引律式(2)与修正后的离散幂次吸引律式(3)的吸引条件是相同的。
定理1对于系统式(1)采用控制律式(4),其误差动态方程可由式(3)描述,则吸引域边界为

即,当| ek | >ΔAB,该闭环系统的误差动态是吸引的。
证明式(3)可写成

判断该闭环系统的吸引性只需考查下述压缩条件

上述不等式可写成
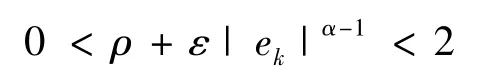
求解该不等式,可得

由式(6)给出的吸引域得证。
下面考虑不同幂次对吸引域的影响。当ε >2-ρ时,吸引域随α单调递增;反之,吸引域随α单调递减。若不加入线性项,易得吸引域为| ek | >。显然,线性项的加入使得吸引域变小了。为考虑线性项的影响,记为

对η(ε) 关于ε求导,可得:

由上式知,dη/dε >0,特别地,η随ε减小而减小,且=0,此时线性项存在与否对吸引域变化的影响也逐渐减小。这样,本文给出了2 个结论:(1)当ρ >0 时,连续吸引律总是吸引的,ρ越大,收敛越快;对于离散吸引律,只有0<ρ <2 时才是吸引的。(2)加入线性项使吸引域变小,通过适当调小ε可减小线性项对吸引域变化的影响。
4 离散吸引过程收敛性分析
下面分析并比较离散吸引律式(3)的各项指标,这里,假设式(3)中的修正项满足| vk+1|≤Δ。
定理2当0<ρ <2 时,该闭环系统的误差动态是绝对吸引的,其吸引层边界为ΔAA,且跟踪误差ek最终会收敛到稳态误差带ΔSS内,其中,



此时,跟踪误差满足ek<ΔSS。
综上,在稳态误差带的边界处,即可得式(9)。当ek <0 时,可得相同边界表达式。
本文依据定理2,针对不同幂次α=分别给出了ΔAA和ΔSS的具体表达式,详细过程如下。

求解上式,可得到绝对吸引层边界ΔAA的表达式

求解上述方程组可得

求解上述方程组可得


在控制器作用下,跟踪误差有限步内可收敛于稳态误差带内,而首次进入稳态误差带所需的最大收敛步数可用于刻画吸引律式(3)的收敛速度。
定理3该闭环系统的跟踪误差首次进入稳态误差带所需的最大步数为max{「k∗⏋,0},其中,「g⏋为向上取整算子。

求解上式可得式(23)。当ek <0 时,容易推得相同结论。特别地,当e0≤ΔSS时,其收敛步数为0。
5 数值仿真与比较
在参数ρ、ε给定时,以α=1/4和α=1/2 为例,本文讨论α对稳态误差带ΔSS的影响。根据式(15)与式(21),存在多种情况确定,为了讨论简便,考虑ΔSS均由确定的情形。记α=1/4 时的稳态误差带为ΔSSI,α=1/2 时的稳态误差带为ΔSSII,则


综上,由情况(1)可知,当ΔSSI与ΔSSII均由ρΔSS+-Δ=0 确定时,它们出现在以ΔSS=1 为分界值的同侧,即(ΔSSI-1)(1 -ΔSSII) >0。由情况(2)和(3)可知,若0 <ΔSS<1 时,即在Δ<ρ+ε条件下,α=1/4 具有较小的稳态误差界,由情况(4)和(5) 可知,当ΔSS>1 时,有Δ >ρ+ε,此时α=1/2 具有较小的稳态误差界。当稳态误差带均由-Δ=0 确定时,在相同参数下,幂次选取α=1/2与α=1/4,依据式(15)和(21)计算所得的稳态误差带结果如表1 所示。
为了仿真验证幂次吸引律式(3)各项性能指标的表达式,包括吸引域、最大收敛步数、绝对吸引层以及稳态误差带,分别选取α=1/2与α=1/4、采样时间Ts=0.01 s,置初始误差e0=0.5 mm,vk=0.1×|mod(k,10)-5|,则| vk |≤0.1,即Δ=0.1。
(1)当α=1/2 时,考虑以下两种情况。
情况1当0<ε≤c0,ε >2(1-ρ)时,ΔSS=ΔAA。参数选取ρ=0.5,ε=0.4 由式(6)、(14)、(15)与(23)计算可得ΔAB=0.0711,ΔSS=ΔAA=0.18,「k∗⏋=1。由图1 可看出,实际收敛步数kt=1。
情况2当c0<ε≤2(1-ρ)ΔAA。参数选取ρ=0.6,ε=0.25 由式(6)、(14)、(15)与(23)计算可得ΔAB=0.0494,ΔAA=0.3144,ΔSS=0.3391,「k∗⏋=3。由图2 可看出,实际收敛步数kt=3。
表1由ρΔSS + -Δ=0 确定ΔSS

表1由ρΔSS + -Δ=0 确定ΔSS

图1当α=1/2,0 <ε≤c0,ε>2(1 -ρ)(Δ/ρ)时的ek

图2当α=1/2,c0 <ε≤2(1 -ρ)(Δ/ρ)时的ek
(2)当α=1/4 时,考虑以下两种情况。
情况3当0 <ΔAA 情况4当c10≤ΔAA<δSS2时,ΔSS>ΔAA。参数选取ρ=0.2,ε=0.2,由式(6)、(20)、(21)与(23)计算可得ΔAB=0.0534,ΔAA=0.1211,ΔSS=0.1595,「k∗⏋=4。由图4 可看出,实际收敛步数kt=3。 图3当α=1/4,0 <ΔAA 图4当α=1/4,c10≤ΔAA <δSS2时的ek 直线电机实验装置见图5,实验装置主要由ELMO 伺服驱动器、TMS320-F2812DSP 开发板和永磁同步直线电机组成。其中,ELMO 交流伺服驱动器以及DSP2812 开发板作为控制器用,采用三环控制,电流环与速度环控制器由ELMO 驱动器提供,位置环由DSP 开发板提供。上位机用于过程监控和数据存储。位置环由DSP 开发板提供。上位机用于过程监控和数据存储。通过系统辨识的最小二乘算法获得伺服对象的数学模型,系统参数a1=-1.9962、a2=0.9962、b1=-2.6757、b2=2.6662。 图5 直线电机实验装置 将系统参数代入控制器式(4)可得到离散时间系统的重复控制器,令N=1 得到相应的反馈控制器。实验中分别采用重复控制器和反馈控制器,使直线电机执行位置跟踪任务。实验目的是验证重复控制器对周期扰动的完全抑制,并结合观测器对非周期扰动的有效抑制。 实验中,直线电机精度为0.5 μm,采样时间为Ts=5 ms,采样周期点数N=800,给定周期参考信号为r(t)=(10sin(2πt) +10)mm。 实验1采用反馈控制器,扰动补偿为=dk,设置参数α=1/2,ρ=0.7,ε=0.3,实验结果如图6 所示,稳态误差收敛至[-6,6] μm。而从误差分布图可知,| ek |≤2 μm 的占比为72%。 图6 采用反馈控制器的跟踪误差 实验2采用重复控制器,扰动补偿为=dk,设置相同的控制器参数,实验结果如图7 所示,稳态误差收敛至[-5,5] μm。而从误差分布图可知,| ek |≤2 μm 的占比为76%。 实验3采用重复控制器,扰动补偿采用观测器式(5)补偿,设置相同的控制器参数,观测器参数设置为β1=0.5、β2=2,实验结果如图8 所示,稳态误差收敛至[-3.5,3.5] μm。而从误差分布图可知,| ek |≤2 μm 的占比为81%。 图8 采用观测器补偿后重复控制器的跟踪误差 从实验结果可以看出:对于周期参考信号,重复控制器可实现周期扰动完全抑制,提高了稳态精度(见图6、7)。进一步由图7、8 可知,在采用观测器补偿后的重复控制器作用下,能有效减小第一周期系统误差,同时其扰动补偿措施能有效抑制非周期扰动,进而改善跟踪性能。 图7 采用重复控制器的跟踪误差 本文提出采用等效扰动补偿的幂次吸引离散重复控制方法,用于解决不确定离散时间系统的周期轨迹跟踪问题。该方法通过观测器估计等效扰动扩张后的新状态达到补偿作用,并将此方法“嵌入”幂次吸引律中构建理想误差动态,依次设计具有周期扰动抑制能力的离散时间重复控制器。文中针对不同幂次,给出了可用于控制器参数整定和表征系统跟踪误差收敛过程的性能指标,包括绝对吸引层、稳态误差带的具体表达式以及系统跟踪误差进入稳态误差带的最大步数。通过数值仿真与直线电机的实验,验证了所提控制方法的有效性。

6 实验结果




7 结论

