考虑配电网电能质量改善的分布式光伏优化调度方法

张敏，祗会强，张世锋，樊瑞，李冉，王金浩

(国网山西省电力公司电力科学研究院，太原市 030001)

0 引 言

为构建清洁低碳的能源体系，应对能源资源紧张、气候变化等挑战，可再生能源发电受到了各国政府的重视并得到迅速发展。分布式光伏发电作为利用可再生能源的一种重要形式，已在中低压配电网中得到了推广应用。然而，随着分布式光伏容量的增加以及大量单相分布式光伏的接入，配电网也将面临电压越限[1]、三相不平衡[2]等电能质量问题。另一方面，不断增加且分布广泛的非线性负荷以及单相负荷也导致配电网的谐波及不平衡问题日趋严重[3]，影响其正常运行。为解决配电网电压越限、三相不平衡和谐波等问题，通常需要安装各种电能质量补偿装置，但这样会增加配电网的投资运行成本。由于分布式光伏的并网逆变器与有源滤波器、静止同步补偿器等装置具有一致的拓扑结构，其在适当的控制下也可发挥电能质量治理功能[4-5]，因此利用分布式光伏自身改善配电网电能质量的方案因其经济性已经在近年来受到了较多关注。

为充分发挥分布式光伏的电能质量补偿能力，国内外学者们针对其优化调度问题开展了广泛研究。文献[6]针对高比例分布式光伏接入导致的电压越限问题，提出一种光伏逆变器的无功调度方法。文献[7]通过对配电网中的可调串联电抗器的电抗值及光伏逆变器的输出无功进行协调优化，在解决电压越限问题的同时还减小了线路有功损耗。文献[8-10]提出了用于配电网电压控制的分布式光伏有功无功优化调度方法。然而，上述研究均在配电网三相平衡的假设下进行，并采用单相配电网模型进行分析，因此建立的优化模型不适用于不平衡配电网。文献[11]针对单相分布式光伏接入配电网引起的不平衡问题，提出了一种光伏选相接入及优化其有功无功输出的方法。而文献[12-13]以改善网损、不平衡等为目标，对中低压配电网中分布式光伏的有功无功输出进行了协调优化。但上述文献并未考虑利用分布式光伏进行配电网谐波问题的优化治理。由于目前配电网中的非线性负荷逐渐呈现出数量多、分布广的特点，传统的单点谐波治理方法不再适用，因此从优化的角度利用分布式光伏改善配电网谐波问题同样值得研究。

分布式光伏优化调度本质上是建立并求解配电网最优潮流(optimal power flow, OPF)模型。在同时考虑改善不平衡以及谐波问题的情况下，OPF模型将包括配电网三相基波潮流和谐波潮流约束，以及对应的三相电压电流变量，是一个复杂的非凸非线性约束优化模型，因此有必要研究此OPF模型的求解算法。由于OPF模型的非凸性质主要源于潮流方程，文献[14]利用一阶泰勒近似方法将不平衡配电网的三相潮流方程线性化。文献[15-16]采用支路潮流等式作为配电网的运行约束条件，并采用变量替换的方式将其松弛为线性不等式约束。文献[17]在三相潮流约束中加入辅助变量，将非凸非线性OPF模型转换为半定规划模型求解。然而，上述近似方法的精度受配电网运行状态的影响较大，根据近似模型优化结果可能不能满足配电网某些运行约束[18]。此外，遗传算法、粒子群算法等智能算法也在配电网OPF模型的求解中得到了一些应用[19-20]，但当变量及约束条件数量较多时，智能算法往往存在计算效率低、解的最优性差等问题，导致其在配电网优化调度中的应用受到限制。

综上所述，本文从利用分布式光伏逆变器输出有功功率后的剩余容量进行配电网电能质量改善的角度出发，研究以综合改善配电网电压越限、三相不平衡、谐波等电能质量问题的分布式光伏优化调度方法，主要贡献如下：

1)以可调度分布式光伏(schedulable distributed photovoltaic, SDPV)三相有功、无功以及谐波电流输出为控制变量，并在考虑配电网三相基波潮流及谐波潮流约束、节点电压约束、光伏逆变器运行约束以及满足光伏三相总有功功率等于直流侧可输出最大有功功率的基础上，建立最小化网络损耗、谐波电压、不平衡电压的配电网OPF模型。该模型采用统一的形式描述相线、中性线以及连接在不同相间的负荷，可适用于不同结构配电网。

2)为稳定高效地求解所建立的配电网OPF模型，提出一种潮流计算与优化计算的两阶段迭代优化求解算法，通过潮流计算对OPF模型中电流变量进行削减，并提出节点电压幅值约束的几何近似方法，将原始非凸非线性OPF模型转换为凸二次约束二次规划模型，使其可以被原对偶内点法快速求解。最后通过潮流计算与优化计算的交替迭代减小模型凸化误差，从而在降低OPF模型求解难度的同时保证解的精度。

3)建立一个162节点三相配电网测试模型并进行算例分析，对采用所提分布式光伏优化调度方法前后的配电网损耗、节点电压越限情况、网络最大负序不平衡度以及最大谐波畸变率进行对比，然后对两阶段优化求解算法的求解误差以及计算效率进行分析，验证所提方法的有效性。

1 多功能分布式光伏发电系统

首先从简单的单相光伏发电系统开始分析，其常见结构如图1所示，主要包括光伏板、直流变流器、逆变器以及输出滤波器。其中，直流侧电容用于实现直流变流器与逆变器的解耦运行。而直流变流器一般采用最大功率点跟踪(maximum power point tracking，MPPT)控制，保证光伏输出最大有功功率。逆变器则采用电压外环电流内环的双环控制策略，以维持直流侧电压的稳定以及输入输出功率的平衡。由于光伏逆变器通常不会持续工作在额定状态，因此在其具有剩余容量时，即可在适当的控制下输出一定量的无功功率及谐波电流，用于改善配电网电能质量。可实现上述功能的控制方案示意如图2、3所示。

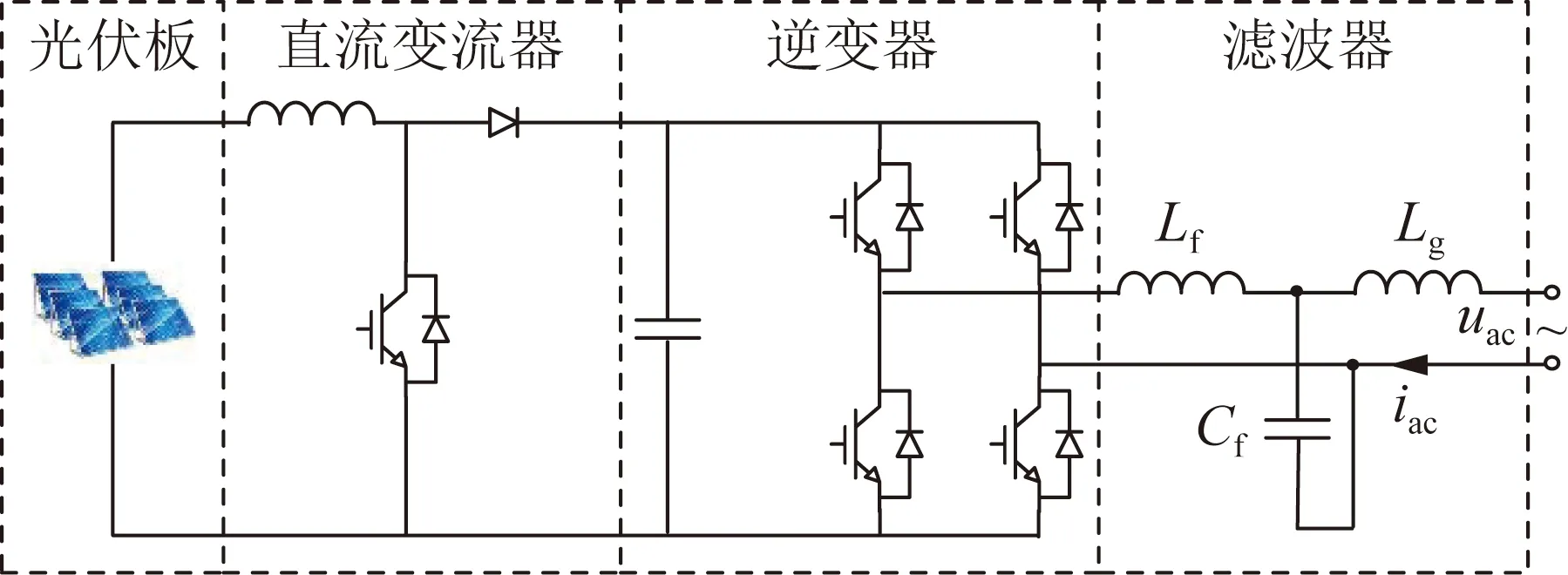
图1 单相分布式光伏发电系统结构

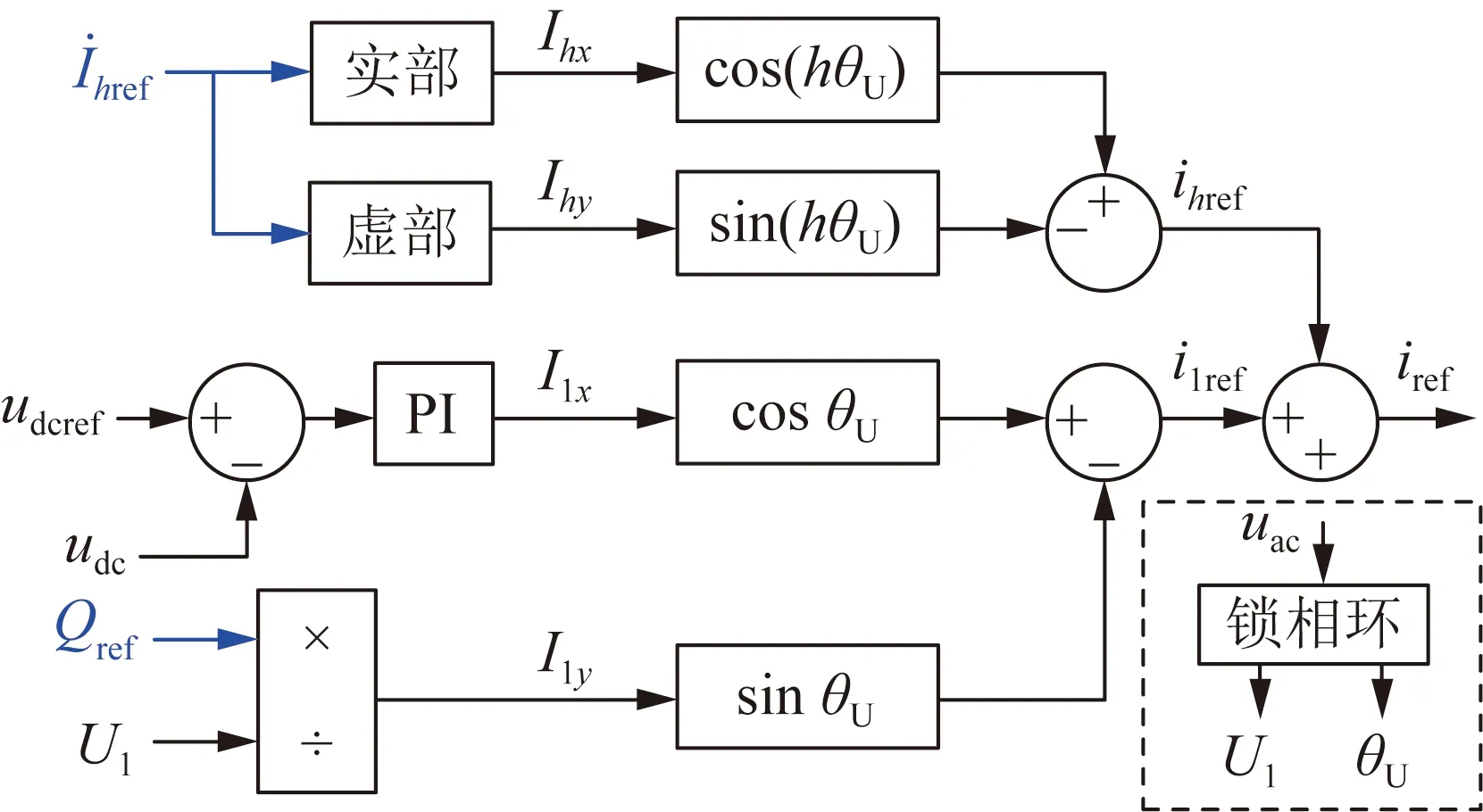
图2 直流电压外环示意图

在图2中，Qref、Ihref及udcref分别为光伏逆变器无功功率输出、谐波电流输出以及直流侧电压参考值；uac、U1及θU分别为并网点电压及其基波分量的幅值和相位；I1x、I1y及Ihx、Ihy分别为光伏输出基波和h次谐波电流相量参考信号的实部与虚部，通过乘以正弦信号，可最终生成光伏输出电流的正弦参考信号iref，然后由图3所示的电流内环对iref进行无差跟踪。图2中，Qref、Ihref可提前设定，也可由调度中心生成并下发给配电网中的可调度分布式光伏。另外，调度中心通过收集配电网运行数据，建立并求解配电网最优潮流模型，还可计算得到各SDPV输出参考值的最优组合，实现对SDPV的优化调度。

图3 电流内环示意图

将图1中的逆变器替换为三相逆变器，即可得到三相分布式光伏发电系统。三相逆变器具有三桥臂、四桥臂以及3个单相逆变器并联而成的组式逆变器等不同结构，其中四桥臂及组式逆变器具有独立调节各相输出的能力，但前者控制相对复杂。为改善配电网三相不平衡问题，本文考虑SDPV的并网接口为组式逆变器，如图4所示，并且其中2台单相逆变器的外环采用图5所示的控制方案，其中，Pref为逆变器有功功率输出参考。由于光伏三相逆变器其中的两相根据Pref的值输出固定有功功率，因此剩余一相逆变器为了维持直流侧电压稳定，其输出有功功率会自动调节从而满足三相逆变器输出有功功率之和等于直流侧输出功率，这使得光伏各相输出功率可在总有功功率输出约束下进行独立调节。在上述条件下，本文后续将对SDPV的有功功率、无功功率及谐波电流的输出进行优化，从而实现配电网的运行优化及谐波畸变、不平衡等电能质量问题的综合优化治理。

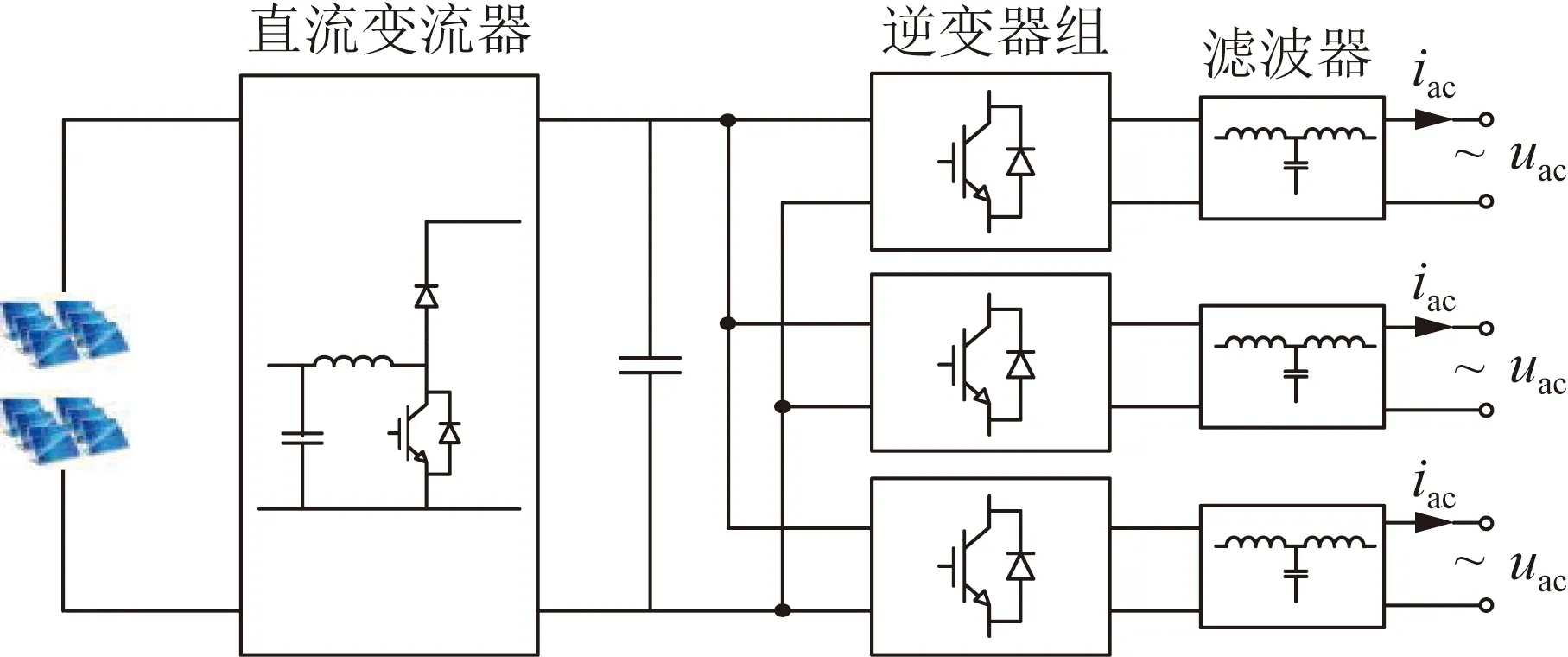
图4 三相分布式光伏发电系统结构

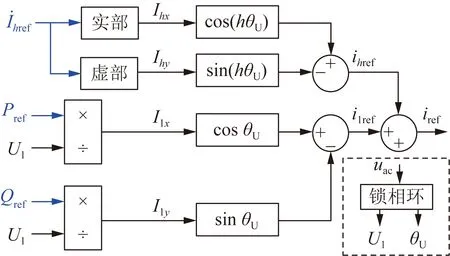
图5 功率外环示意图

2 改善电能质量的最优潮流模型

由于配电网具有单相、三相三线、三相四线等不同网络结构，因此为建立具有通用性的最优潮流模型，本文以三相四线制配电网为例进行建模，对建立的模型进行简化即可得到其他结构配电网的OPF模型。

2.1 目标函数

1)从配电网运行优化的角度出发，要求线路有功功率损耗floss最小化，该项目标函数表达式为：

(1)

2)当配电网中存在非线性负荷时，从改善谐波问题的角度出发，应最小化网络整体的谐波电压水平。

(2)

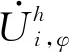
3)当配电网中三相功率不平衡或网络参数本身不对称时，从改善不平衡问题的角度出发，应抑制网络各节点负序电压大小。

(3)

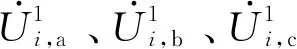
由于多目标优化问题的直接求解较为困难，因此本文通过线性加权[21-23]的方法将上述多个目标函数进行组合得到单目标函数f：

(4)

式中：Floss、Fh、Fu为不同目标函数的归一化系数；ωloss、ωh、ωu为对应目标函数的权重系数，其值越大表示对应的目标函数项优先级越高。在实际应用中，可以根据对电能质量问题的关注度或者严重程度主观设置各权重系数，也可以通过层次分析法[23]等权重决策方法得到更为客观的权重系数。

2.2 约束条件

配电网OPF模型的约束条件包括等式约束及不等式约束，其中，等式约束主要为网络潮流方程，不等式约束则包括节点电压幅值约束、SDPV运行约束等。

1)基波潮流约束如式(5)—(7)所示，其中，式(5)、(6)为非线性等式约束。

(5)

(6)

(7)

对于三相SDPV，其三相逆变器输出有功功率应等于直流侧输出有功功率：

(8)

2)谐波潮流约束如式(9)、(10)所示。本文主要考虑低压台区负荷产生的谐波电流，并采用谐波恒流源模型作为低压台区负荷的谐波模型。

(9)

(10)

3)节点电压约束。为保证配电网的安全运行，通常要求节点电压幅值不能超出一定范围，即满足：

(11)

4)线路电流约束。一般地，需要保证线路上流过的总电流不能过大，因此需要满足：

(12)

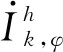
5)电能质量约束。为保证良好的电能质量，要求节点谐波电压及不平衡电压不能过大，即满足：

(13)

(14)

4)SDPV并网逆变器运行约束。为了不影响SDPV的正常工作，应保证其逆变器不过载，因此需要对其输出功率及电流进行限制。

(15)

(16)

结合上述目标函数及约束条件可得，以降低配电网网损，治理谐波及不平衡等电能质量问题为目标，对SDPV进行优化调度的配电网OPF模型为：

(17)

需要注意的是，在OPF模型式(17)中，不等式约束式(11)—(14)和式(15)—(16)之间存在冲突，这是因为在光伏逆变器输出有功功率后剩余容量较少时，其无功功率和谐波电流补偿量也会相应减少，在这种情况下可能就无法保证配电网节点电压或者线路电流等不超标，即出现模型无解的情况，此时可适当放宽或者取消部分电能质量约束，从而在不影响光伏逆变器有功输出的前提下尽力改善配电网电能质量。

3 模型求解流程

3.1 模型凸化过程

求解式(17)即可得到配电网中各SDPV的优化调度方案。然而，式(17)是一个典型的非凸非线性约束优化模型，直接对其进行求解存在计算效率低、收敛难等问题，因此本节中提出一种凸化近似方法，将式(17)转化为更易于求解的凸优化模型。

为了消除非线性等式约束式(5)、(6)、(9)，首先根据当前配电网中低压台区以及SDPV的运行数据进行一次基波潮流与谐波潮流计算，得到各低压台区的基波电流和谐波电流初值，然后将电流初值代入式(7)和(10)中，得到直角坐标系下的线性化潮流方程，如式(18)所示。

(18)

(19)

对于SDPV逆变器容量约束式(15)及(16)，也可通过类似的方式进行凸化，得到新的不等式约束：

(20)

(21)

经过上述近似简化后，只剩节点电压约束式(11)为非凸约束。直角坐标系下的节点电压幅值约束如图6所示。

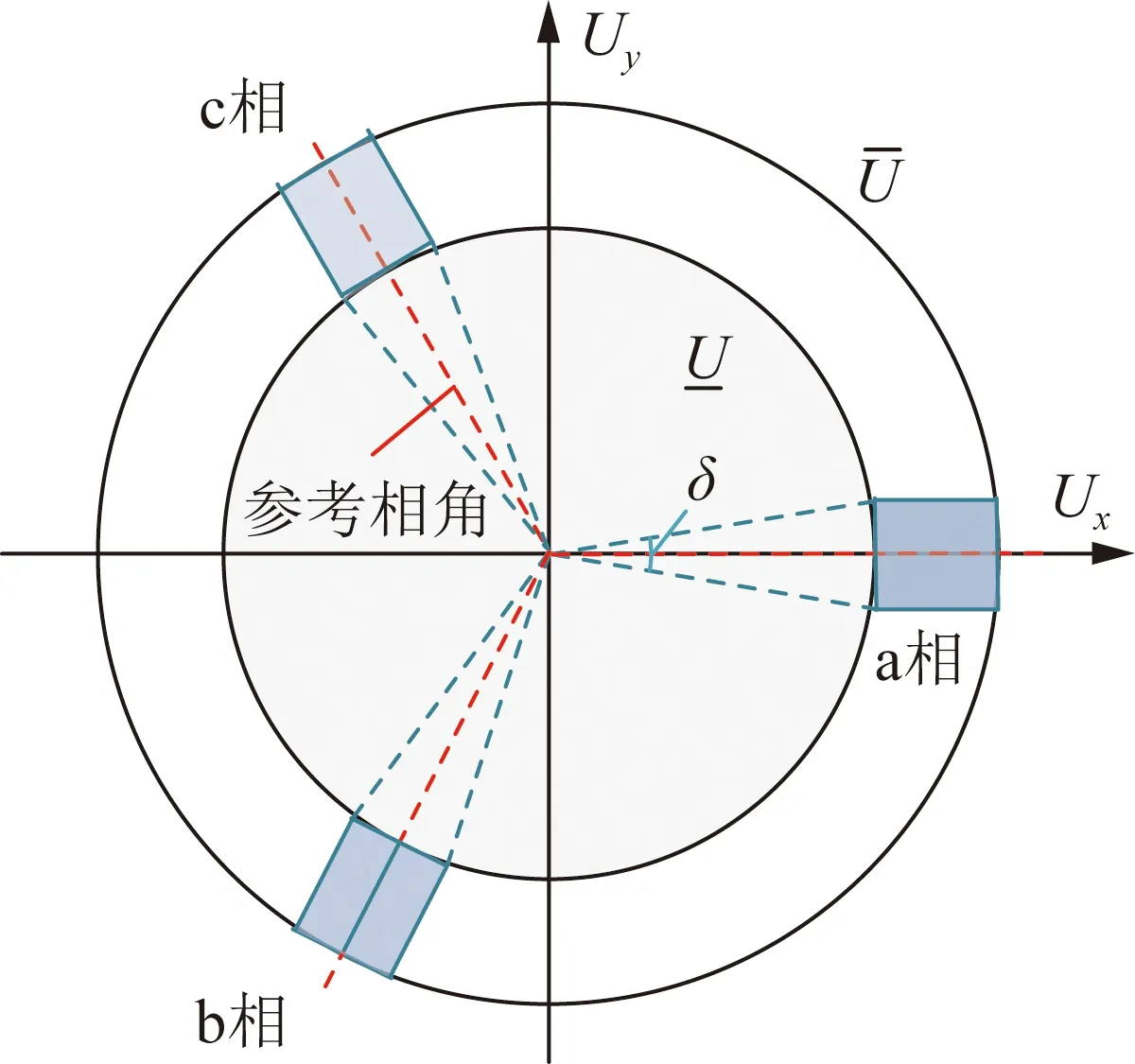
图6 直角坐标下的电压幅值约束

由图6可见，节点电压幅值约束表现为电压上限与下限之间的圆环区域。由于实际配电网各节点电压相角变化范围通常不大，因此可采用某一小段区域近似表示电压约束，例如图6中的蓝色矩形区域。图中的每个矩形区域均可由一组线性不等式描述，以a相为例：

(22)

式中：δ为节点电压相角的变化范围，为保证电压约束近似的合理性，其值应大于节点电压相量相角与参考相角间的最大相角差。但δ的值选得过大，近似精度会下降，在实际应用中，可以通过在优化前对配电网进行潮流计算，得到网络中节点电压相角的变化范围，并据此合理设置δ的值。在本文算例分析中，设置δ=15°。另外，选择合适的参考相角也有助于提高近似精度。

经过上述凸化过程，可得到OPF模型式(17)的凸化近似模型为：

(23)

由于式(23)的目标函数为凸二次函数，等式约束均为线性约束，而不等式约束由线性约束和凸二次约束组成，因此其为凸二次约束二次规划(quadratic constrained quadratic program，QCQP)模型，凸QCQP模型的最优解可通过非线性优化算法，如原对偶内点法[24]，可靠求得。

3.2 两阶段迭代求解

对3.1节中的OPF模型凸化过程进行分析可知，在进行一次潮流计算后，模型中低压台区的电流将不再变化，相当于完全将其视为恒流源，这显然忽略了节点电压对台区输出电流的影响，因此可能导致凸QCQP模型式(23)的优化结果与原OPF模型式(17)之间存在较大差异。为了减小凸化带来的误差，本节提出一种潮流计算与优化计算之间的两阶段迭代优化求解方法，即令潮流计算与优化计算的输出结果互为对方的输入，不断循环迭代，直至计算结果不再发生明显变化。具体步骤如下：

步骤1：根据配电网中低压台区及SDPV当前的运行数据，进行基波潮流及谐波潮流计算，得到低压台区输出基波电流及谐波电流初值，以及SDPV并网点基波电压及谐波电压初值。其中，潮流计算依靠OpenDSS配电网潮流计算软件进行。

步骤2：根据3.1节中的过程，将非凸非线性OPF模型转化为凸QCQP模型。

步骤3：使用原对偶内点算法求解凸QCQP模型。

步骤4：计算步骤3前后模型中各变量值的相对误差。如果误差小于某一阈值，例如0.1%，则将当前计算结果作为最终优化结果输出。否则，将当前优化结果中SDPV的基波功率及谐波电流输出作为输入，返回步骤1进行新一轮计算，直至结果收敛。

4 算例分析

4.1 算例信息

为了验证所提考虑电能质量改善的分布式光伏优化调度算法的有效性，以162节点三相四线制配电网为测试算例进行分析。算例中配电网根据北美某电压等级为13.8 kV的实际配电网改编得到，其拓扑如图7所示，详细的网络参数信息可见文献[25]。在本算例中，设置各目标函数的权重ωloss、ωh、ωu分别为0.70、0.15、0.15。

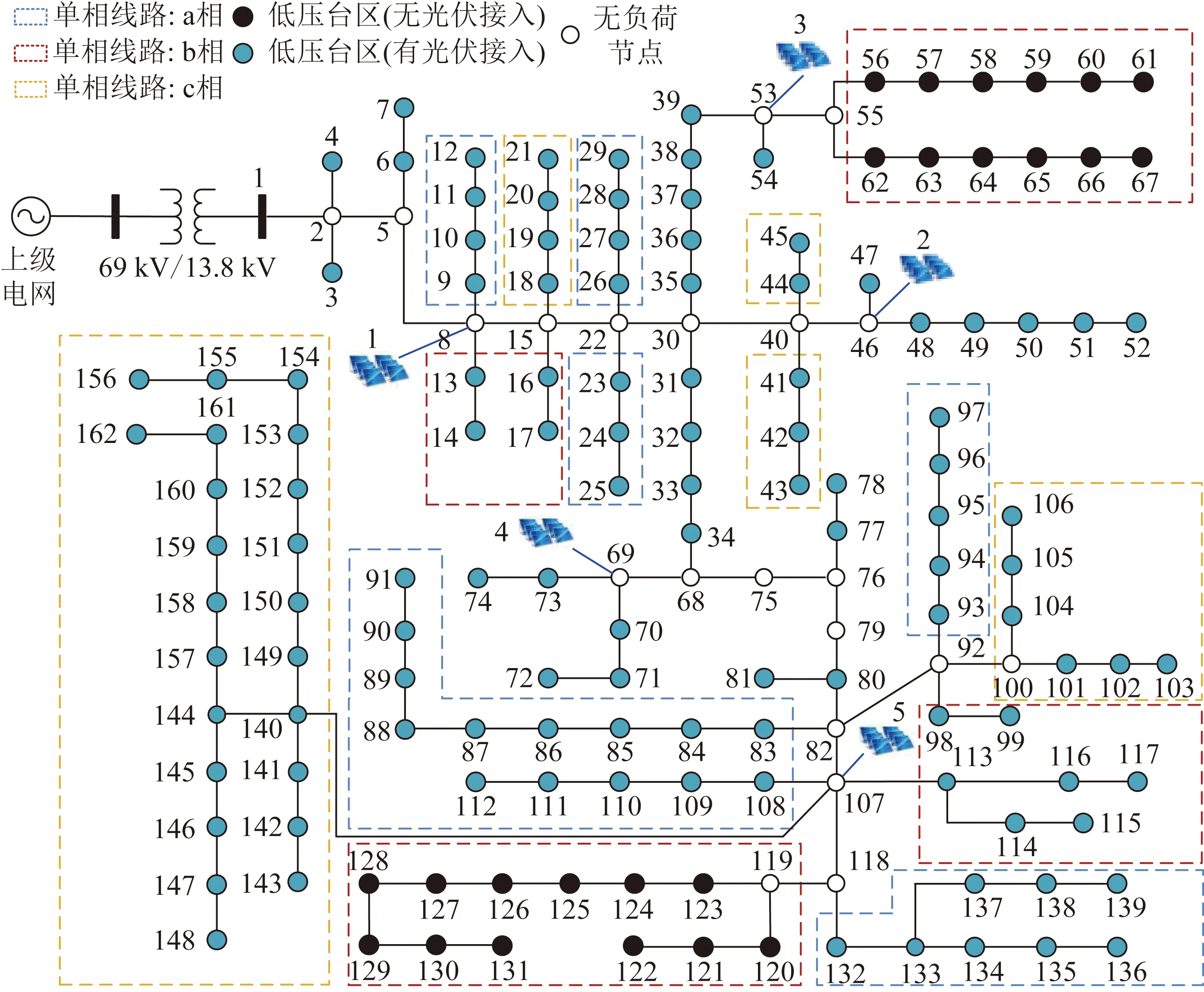
图7 测试配电网结构

算例中低压台区负荷总功率及接入低压台区分布式光伏的总发电功率如图8所示，其中负荷用电高峰主要出现在傍晚，而光伏发电高峰出现在中午。算例的其他基本信息如表1所示。另外，由于中性线的存在，该网络中具有零序谐波电流通路，因此针对谐波问题，本算例将考虑低压台区负荷注入的3、5、7、9次谐波电流的影响，其谐波电流频谱按照低压台区典型谐波频谱进行设置[26]。

图8 低压侧总负荷与总光伏发电功率

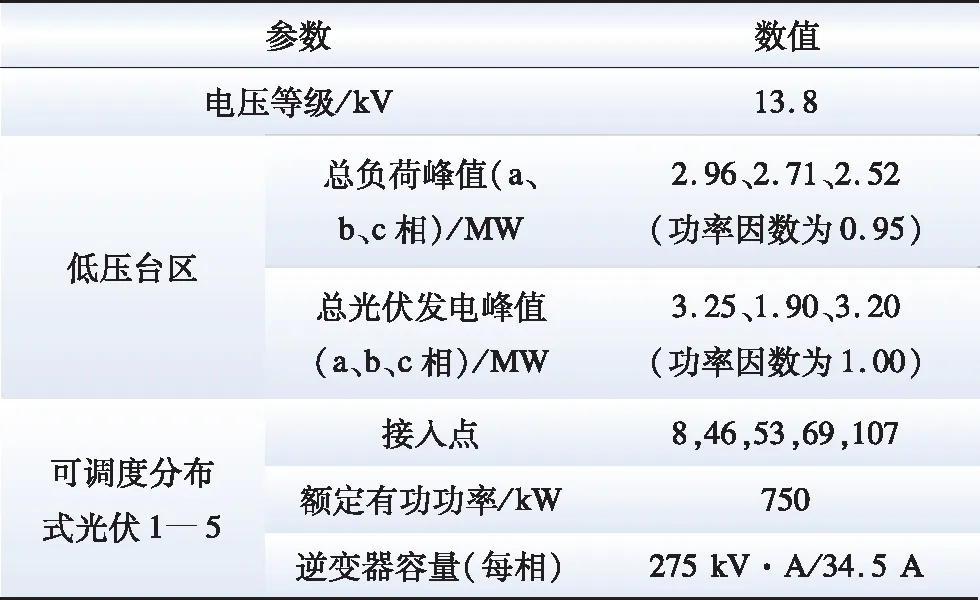
表1 算例基本信息

4.2 结果分析

本算例中，每15 min进行一次优化计算，得到各SDPV的功率及谐波电流优化输出方案，并且认为优化前SDPV仅输出有功功率，且三相输出功率相同。采用所提优化调度方法，得到的12:00以及20:00 SDPV 1—5的各相有功、无功及谐波电流输出分别如图9及图10所示。

图9 可调度光伏在12:00的输出

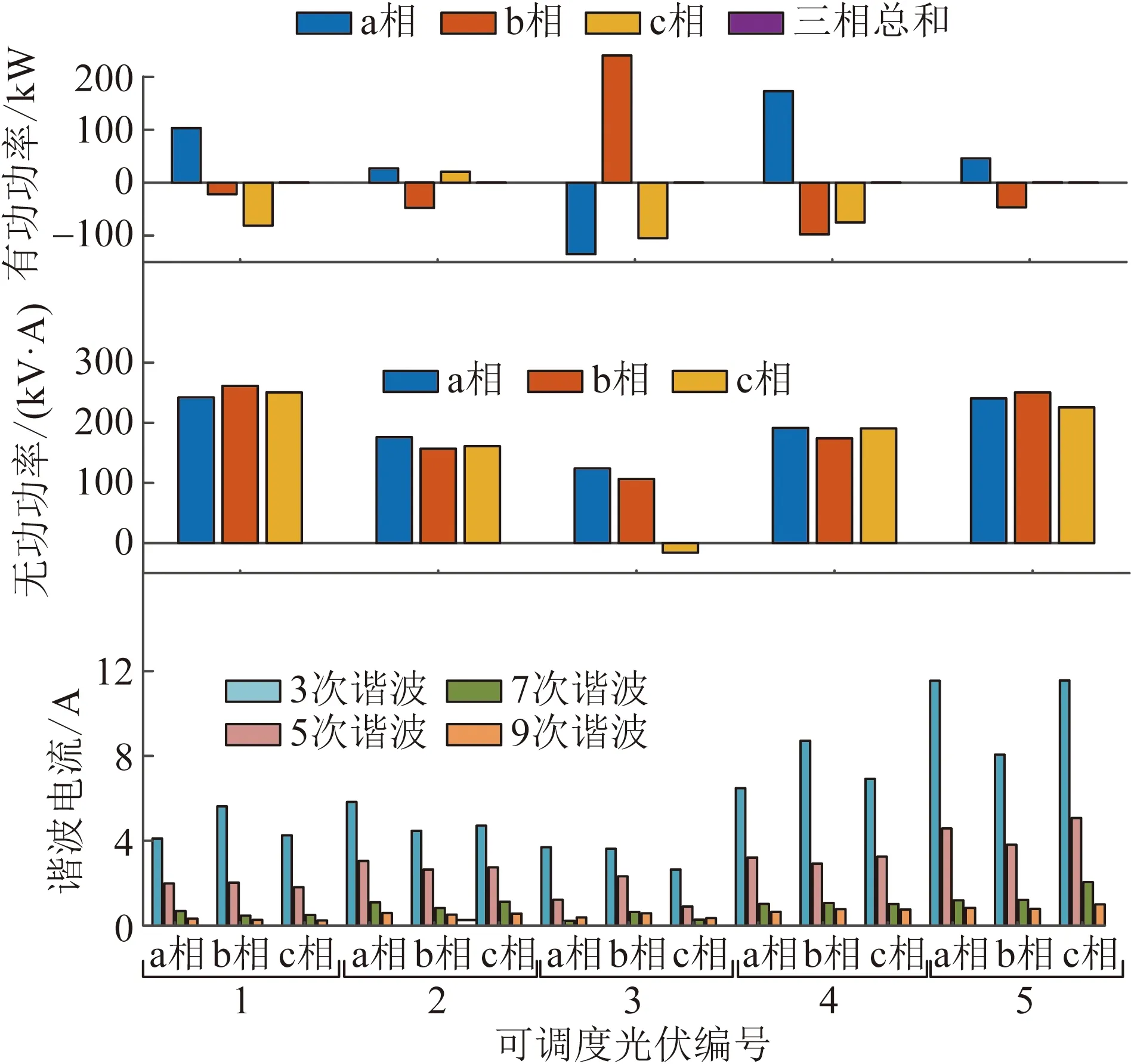
图10 可调度光伏在20:00的输出

在12:00，低压台区接入的分布式光伏发电功率三相不平衡问题较为突出，其中b相的光伏发电功率明显小于其他两相，这将导致配电网不平衡问题加剧。理想情况下，即SDPV逆变器容量充足时，可以依靠在b相输出更多有功功率的方法来改善三相不平衡问题，但是由于此时SDPV自身有功功率输出的需求以及各相逆变器容量的限制，上述方案并不可行。而为了在这种情况下改善网络不平衡问题，在实际优化结果中，可见各SDPV减小了c相有功输出并将该相逆变器容量用于输出更多无功，使得网络各节点c相电压相角偏移减小，三相电压之间的相角差更接近，从而达到减小负序电压的目的。以节点107为例，优化前后电压变化情况如表2所示。另外，可以发现，由于与SDPV5距离更近的低压台区节点数量更多，因此其输出的谐波电流相比其他SDPV也更多一些，从而抵消流向上游线路的负荷谐波电流，改善谐波电流流经线路阻抗造成的电压谐波畸变问题。

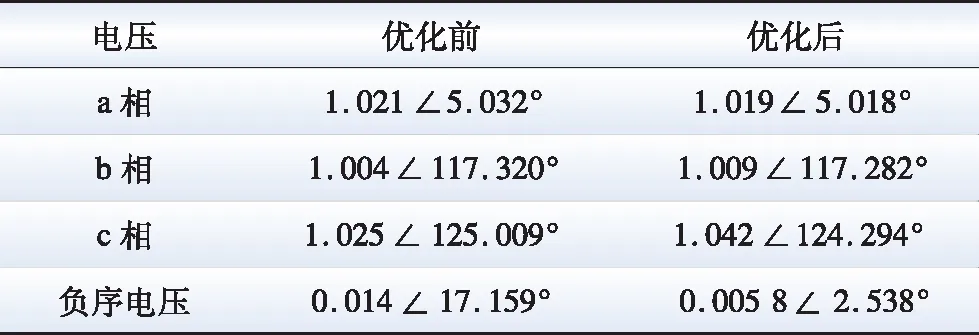
表2 优化前后节点107电压变化

在20：00，各SDPV三相总有功为0，此时逆变器容量较为充足，因此可以在不同相之间进行有功功率的转移来改善负荷三相功率不平衡的问题，同时也能输出充足的无功功率及谐波电流来改善网络中的电压越限以及谐波畸变等问题。

图11展示了优化前后网络节点电压幅值最小值的日变化趋势，图中虚线为设定的电压幅值约束0.95 pu以及1.05 pu。可见，优化前网络最小电压已低于0.92 pu。而按照所提方法对SDPV的功率输出进行优化后，在SDPV逆变器输出无功的作用下，网络中最小电压始终高于0.95 pu，保证了各节点电压均满足运行约束条件。另外，在SDPV输出无功作用下，可见优化后节点电压幅值最大值也有所升高，但由于设置了电压上限约束，因此这种电压幅值的升高将被控制在合理的范围之内，不会造成新的电压过高问题。

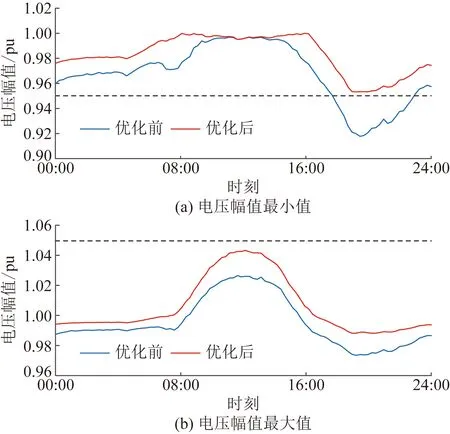
图11 节点电压幅值日变化情况

网络各时刻有功功率损耗情况如图12所示。可见优化后各时刻有功功率损耗有不同程度的降低，其中，负荷功率较大且SDPV逆变器容量充足时，例如20：00，由于可以较多地补偿负荷无功，因此有功损耗降幅相对明显，而在SDPV逆变器容量不足时，例如12:00，其对网络损耗的改善作用也会受到一定限制。另外，将各时刻有功损耗乘以计算时间间隔，可得到优化前配电网总能量损耗约为3.53 MW·h，而优化后，损耗降至2.94 MW·h。

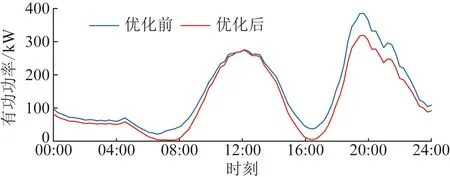
图12 配电网有功损耗日变化情况

图13为网络中负序电压不平衡度最大值的日变化情况。可以看到，根据所提优化调度方法的计算结果调整可调度分布式光伏各相有功及无功功率输出后，网络中的负序电压不平衡度最大值从约1.5%降低至0.6%左右。

图13 负序电压不平衡度最大值日变化情况

图14展示了网络电压总谐波畸变率最大值的变化情况。经过优化后，电压总谐波畸变率最大值从3.57%降至0.48%。另外可以观察到当SDPV并网逆变器的剩余容量充足时，例如16:00—20:00时，配电网节点电压总谐波畸变率在SDPV进行谐波电流补偿后显著降低。然而，当SDPV逆变器容量不足时，例如12:00，此时SDPV需要优先满足其自身有功功率输出需求，因此对谐波畸变问题的改善效果有所减弱。

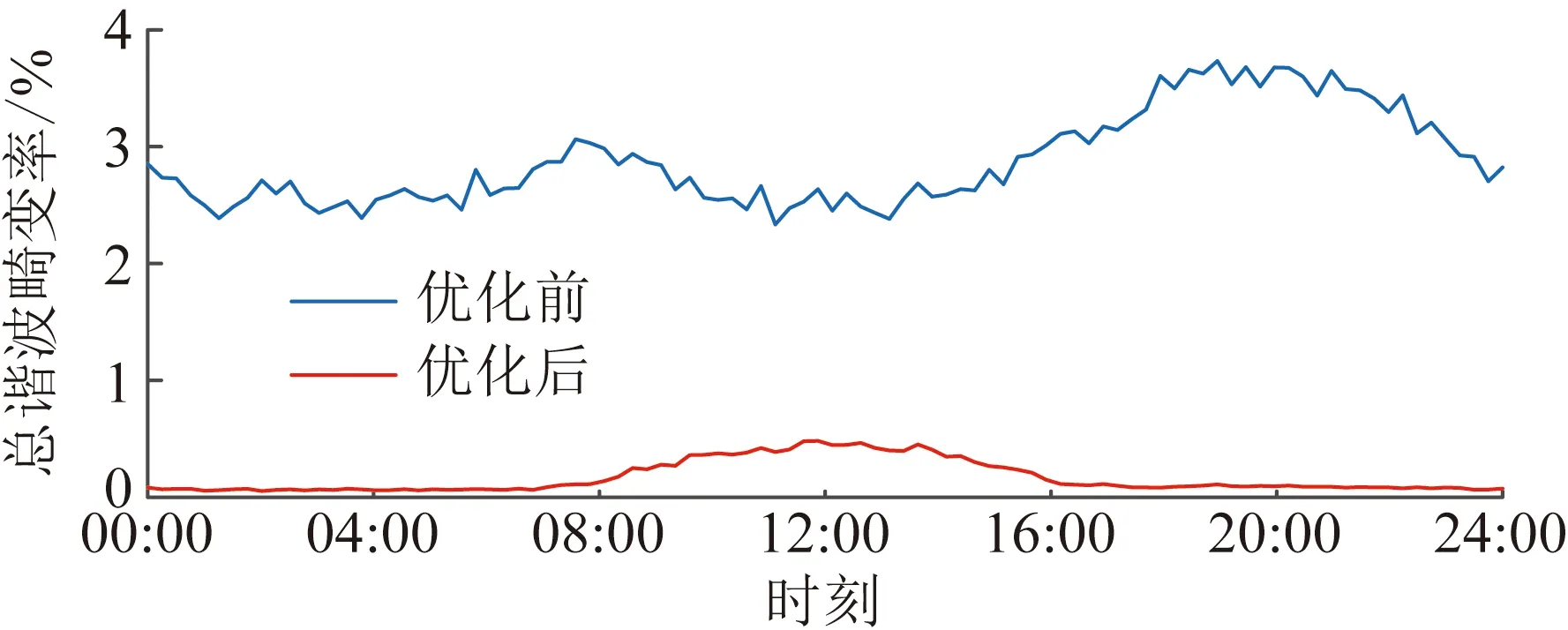
图14 电压总谐波畸变率最大值日变化情况

为了观察目标函数权重系数对优化结果的影响，考虑权重系数ωloss、ωh、ωu分别为(0.70, 0.15, 0.15)、(0.15, 0.70, 0.15)、(0.15, 0.15, 0.70)的3种场景，分别为场景1、2、3，得到20:00的优化结果如表3所示。从表3中可见，权重系数越大，其对应的单项目标函数值越小，表明了通过增大权重系数可以有效增加目标的优先级。另外，通过比较不同场景中目标函数值的差异，可以发现目标函数floss对其权重变化敏感程度较低，这意味着在增大其余目标函数项的权重有助于获得更好的综合优化结果。

表3 不同权重系数下优化结果

4.3 算法性能分析

首先，对电压幅值约束式(22)的近似合理性进行分析。通过潮流计算与优化计算，得到优化前后网络各节点电压相角的变化范围如图15所示，其中，实线和虚线各自围成的区域分别是优化前和优化后节点电压相角的变化范围。可见，在本算例中，选取δ=15°可以完全覆盖各节点电压相角的变化范围，意味着此时δ值的选取是合理的。另外，从图中可以发现，仅针对某一时刻而言，配电网中各节点电压相角的变化范围会更小，因此也可以在不同时刻选取不同的参考相角及δ值，从而进一步提高对原始电压约束式(11)的近似精度。

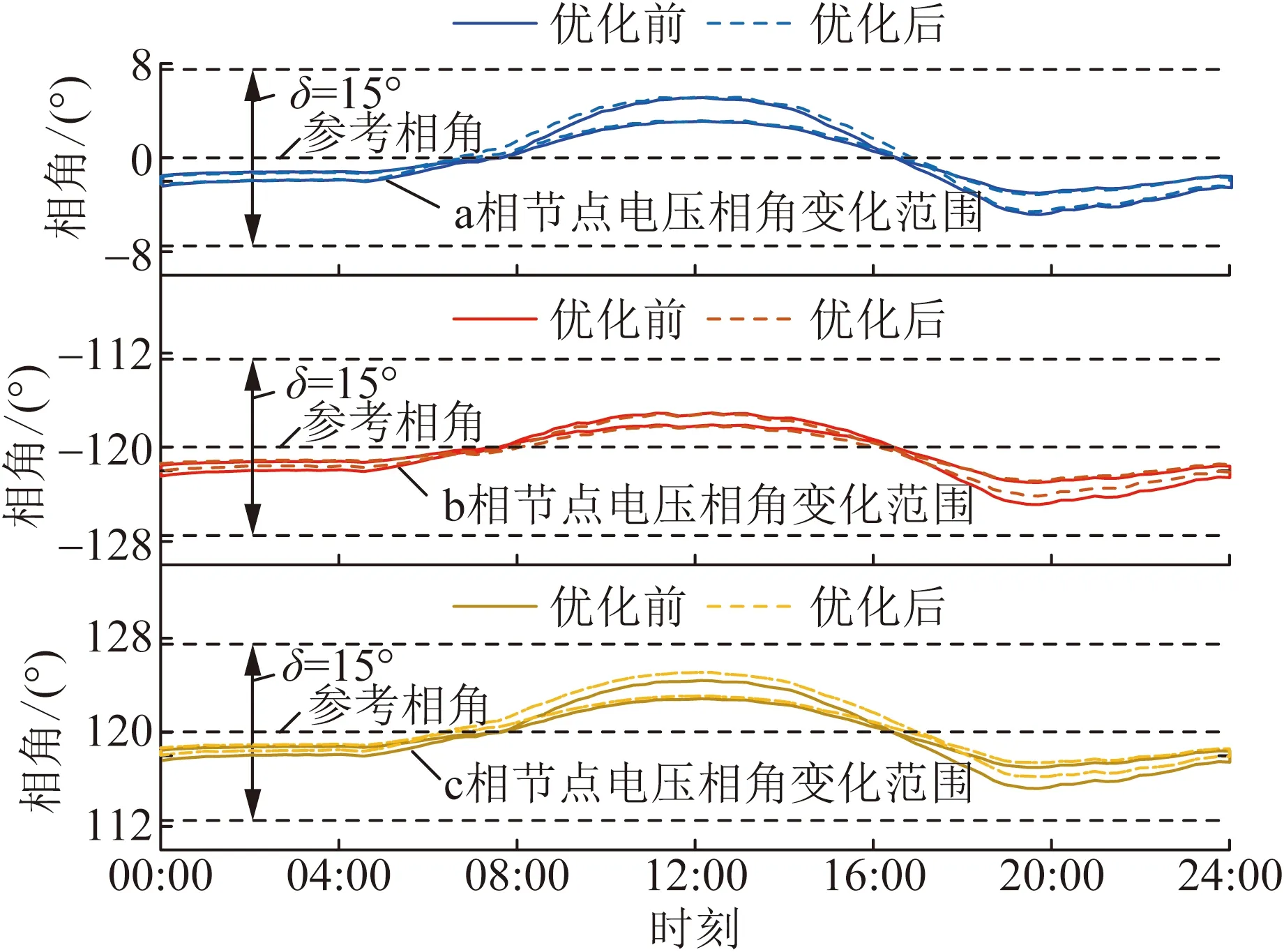
图15 各相节点电压相角变化范围

另外，由于在优化求解过程中对原始OPF模型还采用了其他的凸化近似手段，因此也有必要计算求解过程中凸QCQP模型解与原始OPF模型解之间的误差，误差计算过程如图16所示。其中，将凸QCQP模型解中的控制变量值作为输入代入到基波及谐波潮流计算中，以得到满足原始OPF模型潮流约束条件的一组解。定义节点电压相对误差eU以及约束违反度eh如下：

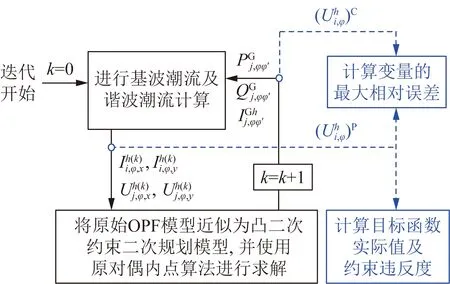
图16 所提优化算法误差分析流程

(24)

不同迭代次数下的eU、eh以及目标函数值如表4所示。可见在迭代次数较少时，凸QCQP模型解与原始OPF模型解之间将存在较大误差，而随着潮流计算与优化计算交替迭代的次数增加，模型误差逐渐减小。在第8次迭代结束后，凸QCQP模型的解已经基本满足原始OPF模型的所有约束，且目标函数值也不再变化。这说明凸QCQP模型的解在原OPF模型中的最优性以及可行性能够随交替迭代次数的增加而得到保证。

表4 不同迭代次数下的模型误差

表4所示迭代过程的计算总用时情况如图17所示，图中也展示了每次迭代过程中使用原对偶内点算法求解凸QCQP模型时的误差下降过程。可以看出，每当原对偶内点算法的内部误差下降到10-6时，即认为本次迭代中凸QCQP模型的最优解已被求得，随后新一轮迭代开始。经过8轮潮流计算与优化计算迭代后，算法最终停止，总用时约为150 s，能够满足通常为15 min进行一次配电网调度的时间要求。

图17 所提两阶段优化算法计算总用时

5 结 论

本文针对如何充分发挥可调度分布式光伏在改善配电网网损、电压越限、三相不平衡以及谐波畸变等问题的能力展开了研究。首先，分析了利用可调度分布式光伏进行配电网电能质量改善的可行性。然后，在配电网三相潮流约束以及其余运行约束条件基础上，以可调度分布式光伏三相有功功率、无功功率以及谐波电流输出为控制变量，建立了一个考虑电能质量改善的配电网最优潮流模型，并提出了一种潮流计算与优化计算交替迭代的两阶段迭代优化算法用于求解最优潮流模型解。算例分析结果表明，本文所提分布式光伏优化调度方法可有效改善配电网电压越限、三相不平衡以及谐波畸变等电能质量问题。下一步将进一步研究多种类型分布式电源以及电能质量治理装置共同参与的配电网优化运行策略。