柔性直流电网直流侧故障下500 kV混合式直流断路器暂态电流特性分析

文卫兵，魏争，赖佳祥，石岩，杨勇，王加龙

(1. 国网经济技术研究院有限公司, 北京市 102209；2. 美国亚利桑那州立大学艾尔·富尔顿工程学院，美国亚利桑那州坦佩 85282)

0 引 言

大力推进新能源开发利用是实现能源结构转型、保障国家能源安全的重要途径。但是，风电、光伏等新能源发电波动性大、可控性弱，并网送出面临巨大技术挑战。柔性直流电网不仅可以发挥柔性直流输电在新能源开发、利用上的技术优势，还可实现多电源供电和多落点受电，通路冗余性强，非常适合解决大规模新能源并网和送出难题[1-2]。然而，柔性直流电网具有低惯性、弱阻尼特征[3]，直流侧故障发展速度极快，易导致柔性直流换流阀等设备损坏。通过交流断路器或全桥换流器处理柔性直流电网中的直流侧故障，会在一段时间内导致电网中故障极全部换流器功率传输中断[4]，进而造成孤岛接入柔性直流电网的新能源电场出现大面积风机无序脱网等严重后果。直流断路器能够快速开断直流短路电流，选择性隔离故障元件，维持柔性直流电网功率输送，是突破上述瓶颈的有效甚至唯一技术手段[5]。

直流断路器主要分为机械式、固态式和混合式3类[6]。其中，混合式因通态损耗小、无电弧烧蚀、易于同时实现高换流速度和高可靠性而受到广泛关注[6-10]。柔性直流电网直流侧故障下，混合式直流断路器所承受故障电流的发展速度可达每毫秒数千安。研究该场景下混合式直流断路器暂态电流特性，对于直流断路器主支路、转移支路中电力电子阀组的设计及器件选型具有重要的指导意义。

针对柔性直流系统直流侧故障下的暂态电流特性，文献[11]分析了柔性直流换流阀直流双极短路的故障机制，文献[12]分析了柔性直流系统的直流侧故障原理及浪涌电流计算方法。但上述文献未考虑柔性直流电网中的短路电流特性。文献[13]研究了柔性直流系统双极短路故障电流计算方法，并将结论延伸至直流电网；文献[14]提出了柔性直流电网单极接地、单极接中性线故障下的暂态电流分析方法；文献[15]提出了一种直流电网极间短路故障电流计算方法，通过建立故障矩阵实现各支路暂态电流计算；文献[16]提出了一种真双极柔性直流电网单极接地短路电流计算方法。但上述研究未考虑短路故障后柔性直流电网真实控制保护逻辑和各交、直流断路器的复杂动作时序，以及由此导致的直流断路器暂态电流流通路径和幅值变化率随时间变化的情况。而在真实控制保护逻辑下，直流断路器暂态电流通路和变化率均具有时变特性。目前尚无针对真实控制保护逻辑下直流断路器暂态电流特性的相关研究。

针对上述问题，本文以张北±500 kV柔性直流电网工程为背景，基于真实控制保护逻辑，对500 kV混合式直流断路器暂态电流特性进行研究，分析柔性直流电网保护动作各阶段下的故障等效电路，推导各阶段直流断路器暂态电流的计算表达式，给出各支路暂态电流应力典型波形及柔性直流电网主回路参数对其影响规律。针对直流断路器主支路暂态电流应力严酷问题，提出一种基于换流站内阻尼电阻的暂态电流抑制方法。最终通过电磁暂态仿真对理论分析结果和所提出方法进行验证。

1 混合式直流断路器工作机理

混合式直流断路器结构如图1所示，由主支路、转移支路和耗能支路三部分组成。主支路由快速机械开关S和小规模电力电子开关Q1串联构成。转移支路由大规模电力电子开关Q2构成。耗能支路由金属氧化物非线性电阻器(metal oxide varistors, MOV)单元串并联构成。Q1和Q2均为子单元串并联结构，子单元中开关器件通常采用绝缘栅双极性晶体管(insulated gate bipolar transistor，IGBT)。

图1 混合式直流断路器拓扑

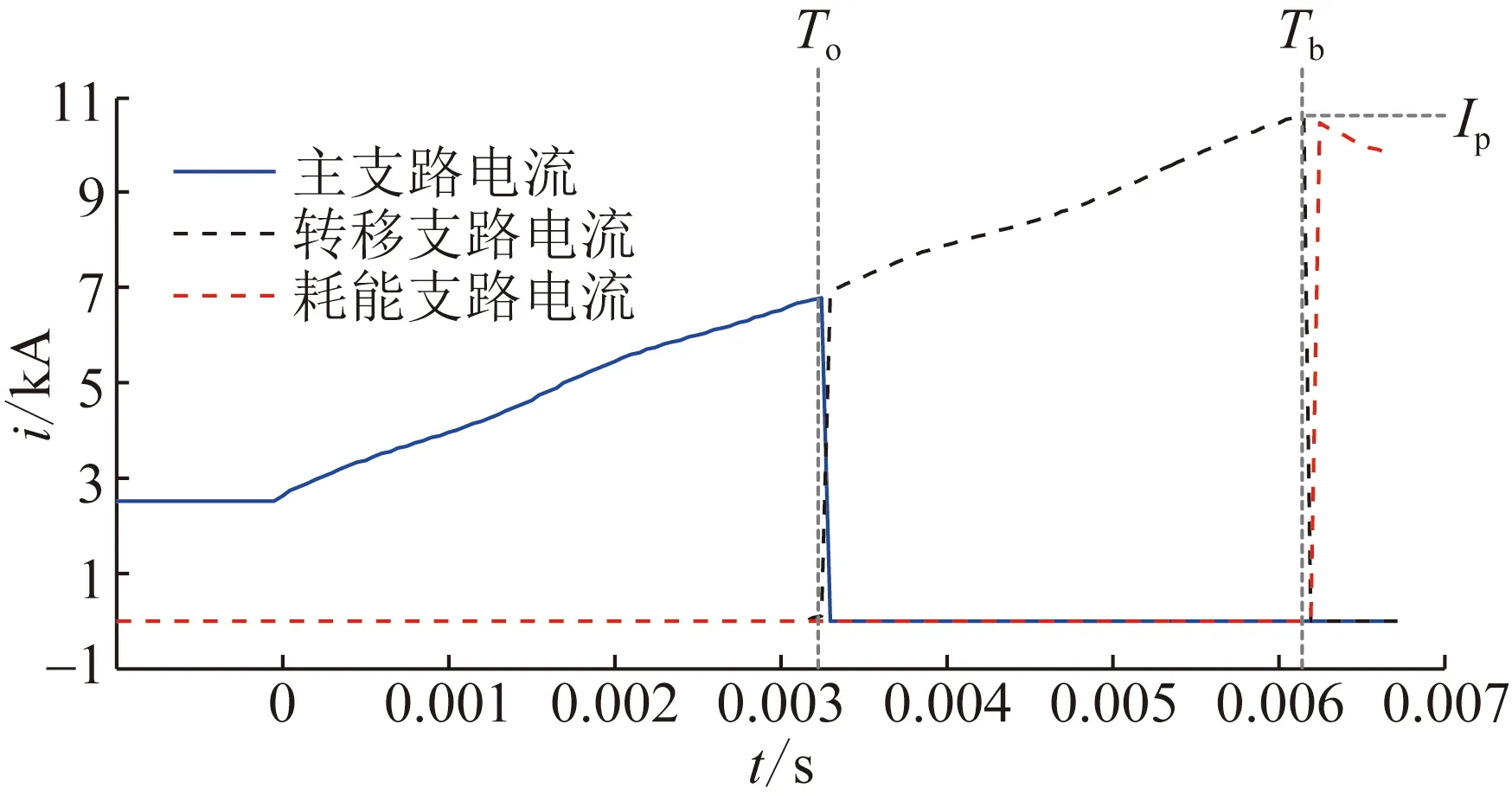
混合式直流断路器开断过程中，主支路、转移支路和耗能支路电流i1、i2、i3及端间电压u的波形如图2所示。故障前，主支路承担稳态电流。t=0时故障发生，i1开始增大。To时刻直流断路器接到分闸指令，闭锁Q1，导通Q2，电流向转移支路转移。换流完成后，i2逐渐增大，S在零电流下开始无弧分断。Tb时刻S各串联断口达到可耐受恢复电压的开距，闭锁Q2，电流向耗能支路转移，导致u升高。换流完成后，u达到最大值，i3逐渐减小，MOV吸收能量，并最终实现直流开断。

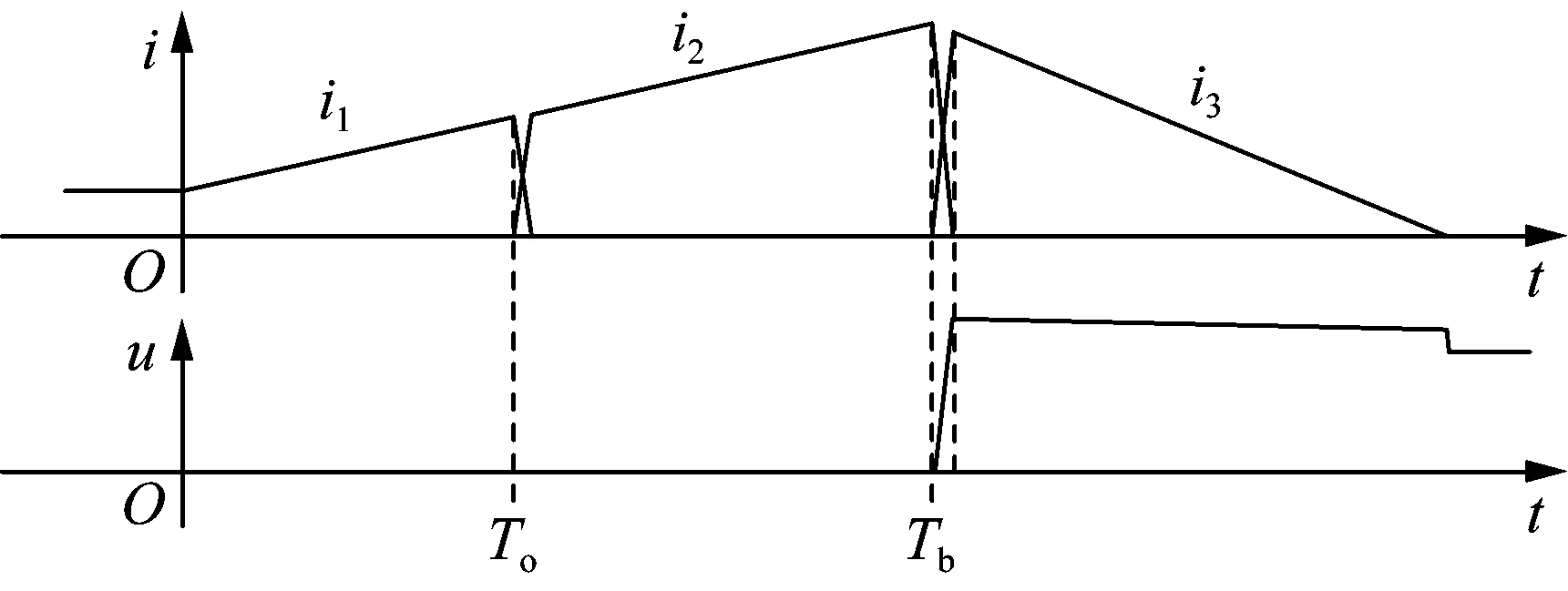
图2 混合式断路器各支路电流和电压波形示意图

2 柔性直流电网结构及故障工况

张北±500 kV柔性直流电网工程采用半桥模块化多电平换流器和双极接线方式，如图3所示。换流站1、2为送端，3、4为受端。以站1正极为例，主接线如图4所示。相邻两站极母线和中性母线分别通过极线路和金属中线联接。换流站4中性母线接地。

图3 四端柔性直流电网的网架结构

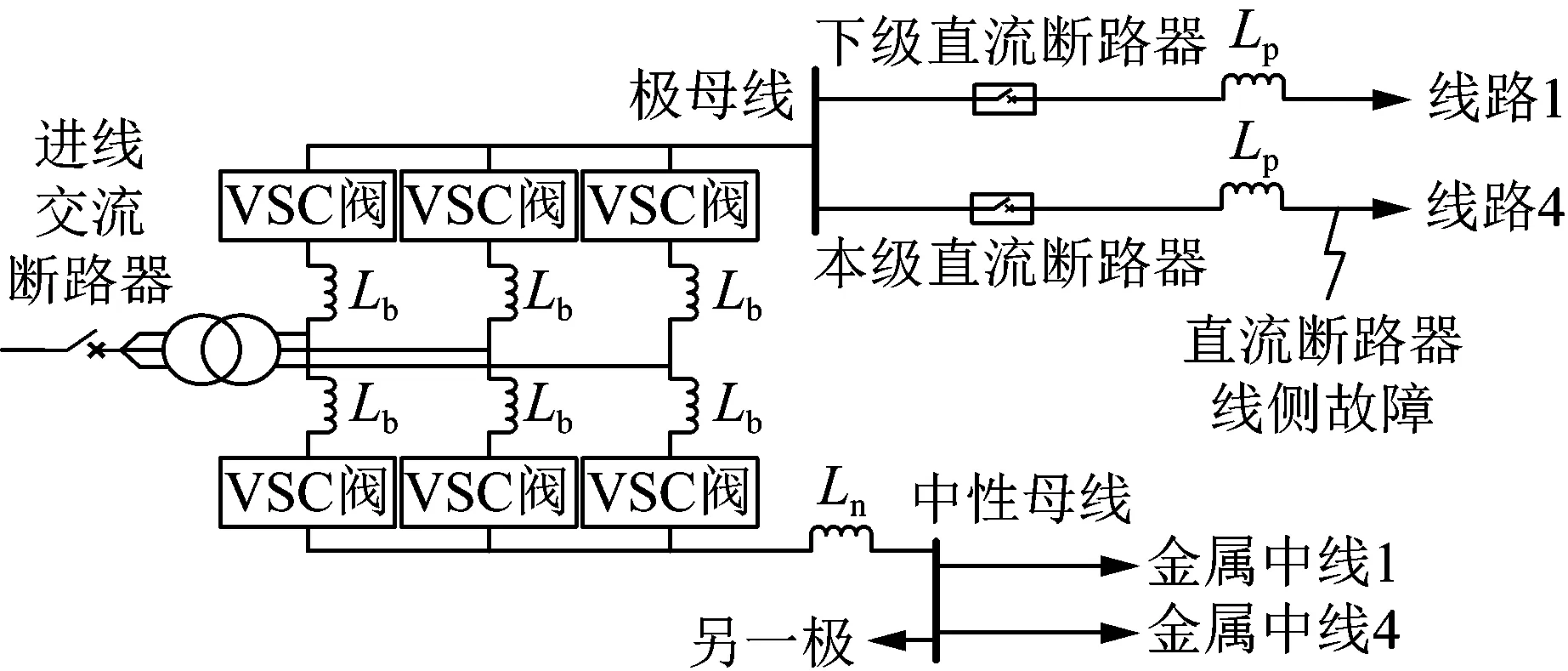
图4 站1正极主接线

以图4中线路4上的直流断路器为例：若故障发生在直流断路器站1侧，则断路器暂态电流主要由远端的站4等馈入；若故障发生在线路4侧，其暂态电流主要由近端的站1等馈入。因此，线侧故障下直流断路器的暂态电流更加严酷。线侧故障包括单极接地、单极对金属中线短路和双极接地，三者的故障等效回路结构相同，仅回路中阻抗大小不同，因此暂态电流变化规律相同。不失一般性，本文以直流断路器线侧单极对金属中线短路为例进行分析，故障位置如图4所示。定义距离该故障最近的直流断路器为本级直流断路器，如图4所示，本文主要研究本级直流断路器暂态电流。与本级直流断路器位于同一极母线上的为下级直流断路器。

上述故障后，应依靠本级直流断路器切除故障线路，健全元件不停运。此时，多站短路电流经本级直流断路器汇入故障点，在该断路器上产生严酷的暂态电流。此外，类比于交流电网，对于柔性直流电网故障后本级直流断路器失灵的情况，应利用相邻的故障隔离设备清除故障[17]，即跳开下级直流断路器、闭锁近端换流器并跳开进线交流断路器。此过程中，失灵直流断路器在较长时间内耐受严酷的暂态电流。因此，需针对故障后本级直流断路器正常动作和失灵的工况，对其暂态电流特性进行分析。

3 理论分析

3.1 正常动作直流断路器的暂态电流特性

3.1.1 单个换流器引起的直流断路器暂态电流

设稳态下线路1通道退出，站1正极换流器仅由线路4输送功率。图4中故障发生后，由于柔性直流电网继电保护和直流断路器动作速度较快，Tb通常仅为6～7 ms[17-18]。此过程中换流器不闭锁，等效为RLC串联电路[13]。故障等效电路如图5所示。图中：Ron为单桥臂开关管导通电阻之和；C为子模块电容；RTL和LTL为故障回路所含极线路和金属中线等效总电阻和总电感；Req=2Ron/3+RTL;Leq=2Lb/3+Lp+LTL+Ln;Ceq=6C/N；Lb、Lp、Ln分别为桥臂电抗、极线限流电抗和中性线限流电抗的电感值。

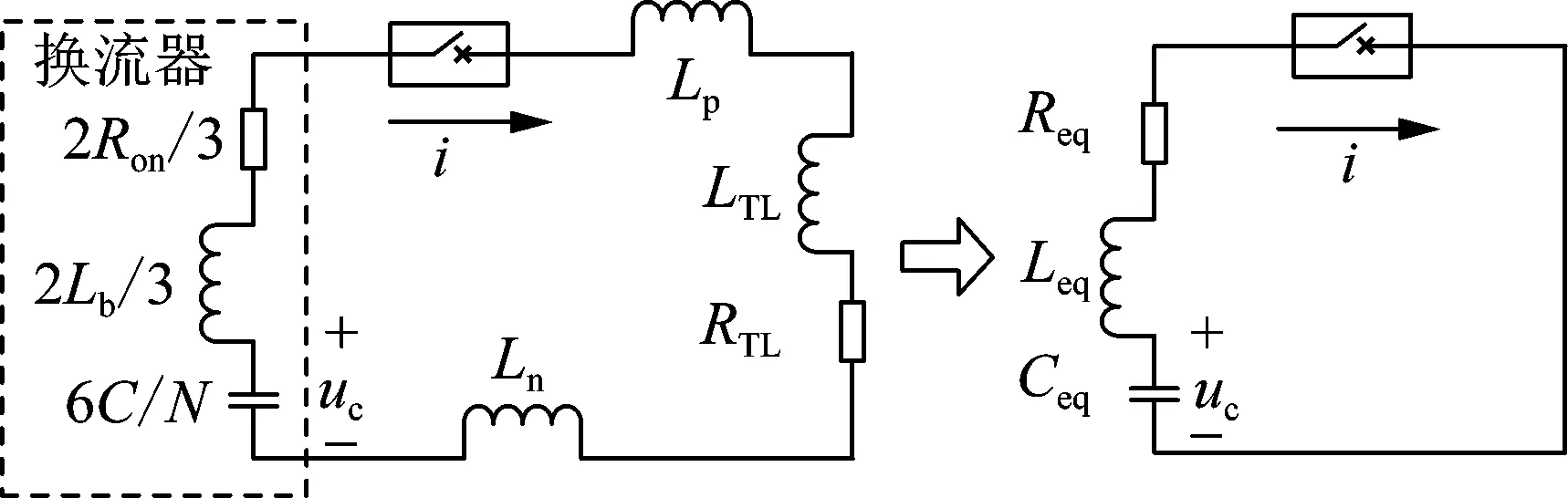
图5 单个换流器引起直流断路器暂态电流的故障等效电路

设故障发生时刻t=0，等效电容的初始电压为换流器端口稳态电压Udc，回路初始电流为线路4稳态电流I0。求解电容电压uc和直流断路器电流i可得：

(1)

式中：Req和Leq分别为故障等效电路中的电阻和电感，如图5所示。

通常Req较小，ω0≫δ，在毫秒级时间Tb内可忽略i(t)指数衰减项，由式(1)可得：

(2)

图5中的电感和电容在H和mF量级，I0在kA级，duc/dt约为数kA/ms。在Tb内Udc≫|duc|，可认为cos(ω0t)=1，sin(ω0t)=ω0t。代入式(2)，可得单个换流器引起的直流断路器暂态电流：

(3)

Q2闭锁后，式(3)中i(t)因MOV投入由上升转为下降。

3.1.2 柔性直流电网中的直流断路器暂态电流

设稳态下电网各元件正常运行，t=0时发生图4所示故障。在Tb内，各换流站放电规律与3.1.1节分析相同，由此得到图6所示的柔性直流电网故障等效电路，电路满足线性叠加原理，本级直流断路器总电流为故障前稳态值I0_DCB与故障后各换流站对暂态电流增量的贡献之和，即：

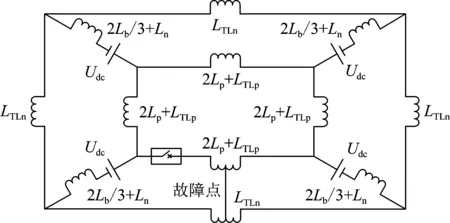
图6 0≤t≤Tb时的柔性直流电网等效电路

(4)

式中：I0_DCB为故障前本级直流断路器总稳态电流；kjUdct为各站对暂态电流增量的贡献，j为换流站编号，kj由j站向直流断路器馈入电流通路中的等效电感决定，电感越小则kj越大。i(t)波形如图7所示。

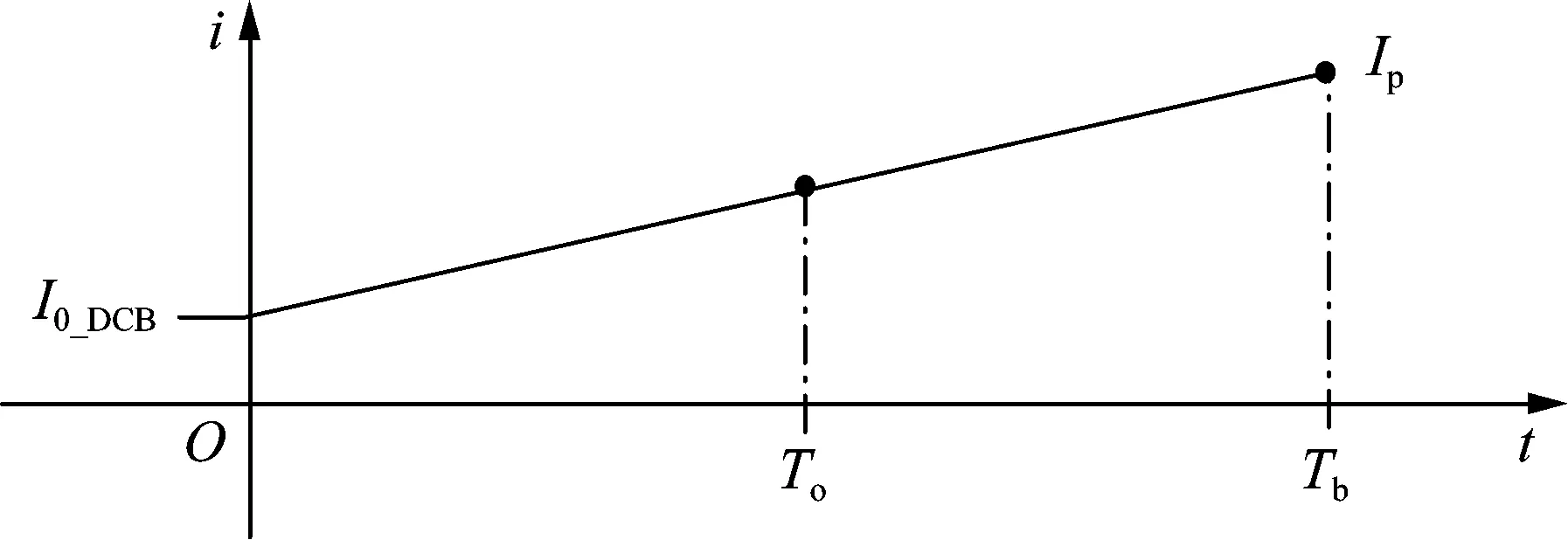
图7 直流断路器正常动作情况下的暂态电流波形示意图

由于故障点将线路4隔离成两段，使得相比于换流站1馈入电流的通路，站3和站4馈入电流通路的路程更远，包含电抗更多，回路电感更大，对应产生的电流分量远小于站1提供的分量，因此式(4)中站3和站4电流分量k3Udct和k4Udct可忽略。

式(4)中i(t)在Tb时刻达到峰值Ip，该值为转移支路元件需承受的峰值和开断电流应力，也是确定Q2中IGBT并联数的主要依据。由于Tb和Udc为确定值，Ip仅由I0_DCB和故障通路等效电感决定。

3.2 失灵直流断路器的暂态电流特性

设稳态下电网各元件正常运行，t=0时发生图4中故障，且本级直流断路器失灵。失灵断路器暂态电流i(t)主要由各站经该断路器馈入故障点的短路电流叠加而成。如前所述，主要针对站1和站2的贡献进行分析。柔性直流电网动作时序如图8所示。

图8 直流断路器失灵情况下的动作时序

i(t)的发展过程分为5个阶段。第1—5阶段中的柔性直流电网故障等效电路分别如图9(a)—(e)所示。

图9 直流断路器失灵情况下的柔性直流电网故障等效电路

第1阶段为0≤t≤T1，各元件均未动作，此时有：

i(t)=k1Udct+k2Udct+I0_DCB

(5)

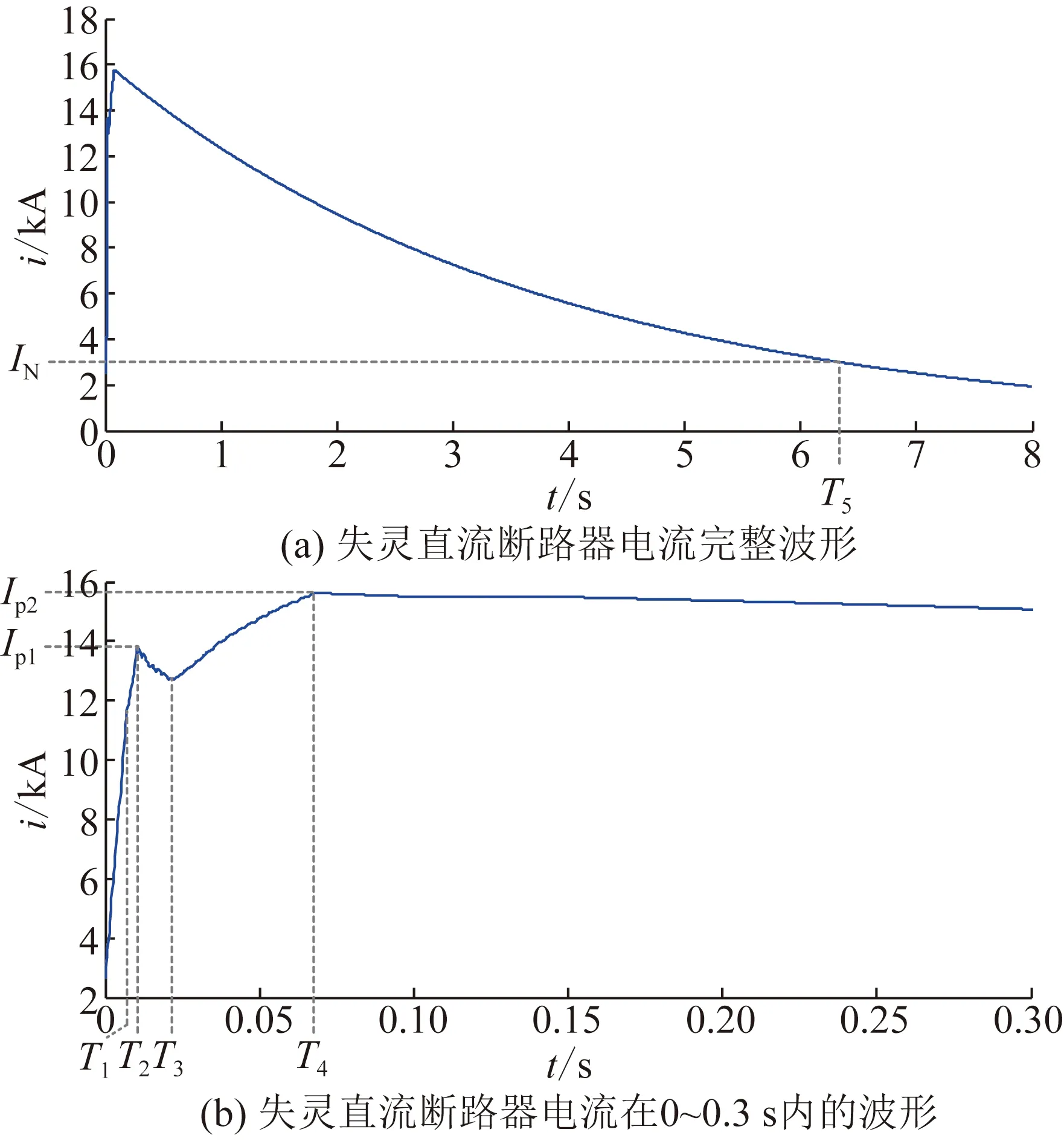
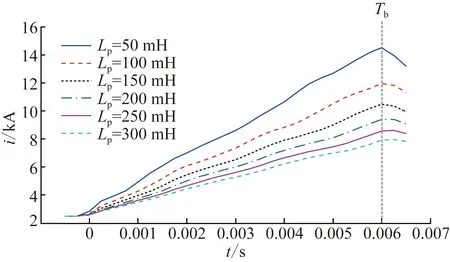
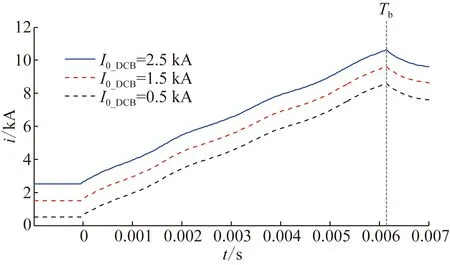
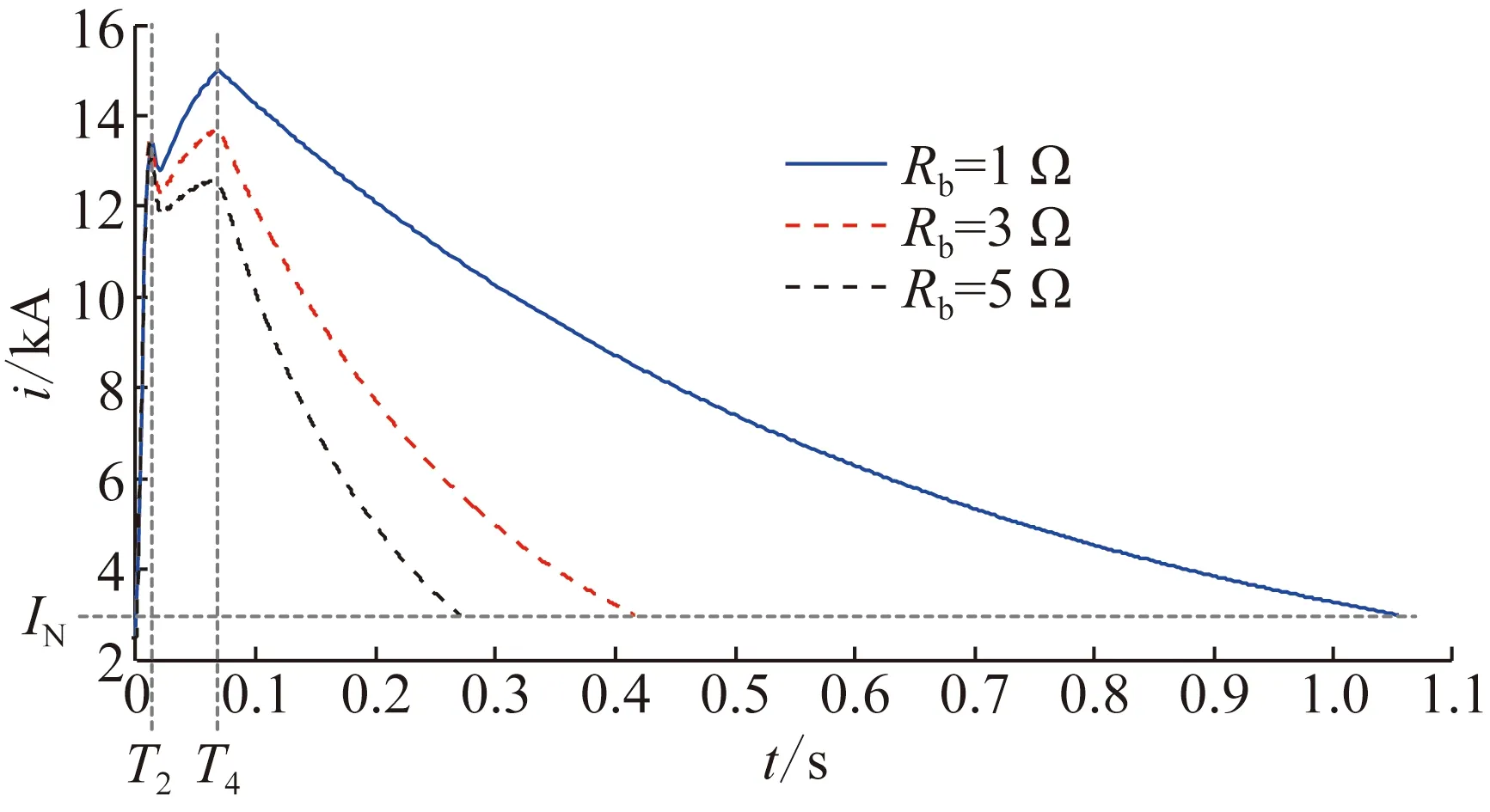
第2阶段为T1

(6)

第3阶段为T2

(7)

式中：Umov为MOV投入时的端电压，约为1.5Udc，用以制造反压，快速开断电流。因此，站2提供的电流分量(等式右侧第2项)快速减小，其衰减速度通常高于站1馈入电流上升速度，使得总电流i(t)开始减小。

第4阶段为T3

(8)

站2提供的电流分量在T3时刻降为0，此后维持在0(下级断路器完全断开)，T3后仅剩站1提供的上升电流分量，因此第4阶段中i(t)逐渐增大。

第5阶段为T4

(9)

i(t)对应波形如图10所示，在T2达到峰值(或拐点)Ip1，在T4达到峰值Ip2，在T5降回额定值IN。

图10所示i(t)即为失灵直流断路器主支路需承受的短时电流应力，也是确定主支路元件并联数的主要依据。短时电流应力主要对主支路元件造成热效应的考验，i(t)产生的热效应可表示为：

图10 直流断路器失灵情况下暂态电流波形示意图

(10)

3.3 直流断路器暂态电流应力抑制措施

如前所述，为抑制直流断路器暂态电流i(t)，即减小特征参数Ip、Ip1、Ip2和T5，需改变I0_DCB或柔性直流电网中的电感、电阻值。由式(5)—(9)和图7、10可知：

1)增大柔性直流电网主回路中的电感，可降低i(t)上升速度，由于保护动作时间已确定，最终可减小Ip、Ip1、Ip2。但增大电感也会降低i(t)下降速度，因此无法确保主支路短时电流持续时间T5减小。

2)减小电流I0_DCB可起到减小峰值Ip、Ip1、Ip2的作用；但由于I0_DCB相对较小，在长时间尺度下早已逐渐衰减到零，因此改变I0_DCB对于长达秒级的主支路短时电流持续时间T5的影响较小。

可见，增大回路电感和减小I0_DCB难以改善T5。T5过长将导致主支路热效应严酷，影响设备安全运行，导致元件性能要求和设备造价大幅提升。

为此，本文提出在换流站内增加阻尼电阻抑制直流断路器主支路暂态电流应力的方法。所增加阻尼电阻的配置方法如图11所示，在换流阀每个桥臂上，新增阻尼电阻Rb与IGBT-二极管对并联，之后与桥臂阀组串联。新增阻尼电阻投入策略如下：

图11 新增阻尼电阻工作状态

1)电压源型换流器(voltage sourced converter, VSC)阀运行时，阻尼电阻并联的IGBT-二极管对导通，将电阻旁路，避免其产生稳态损耗；

2)一旦VSC阀闭锁，则立刻闭锁阻尼电阻并联IGBT，将阻尼电阻投入。

对于故障后直流断路器失灵工况，新增阻尼电阻对断路器主支路暂态电流的抑制作用分析如下：

1)站1中的阻尼电阻在T1时刻站1换流阀闭锁的同时投入。此后，T1

2)在T4

图12 T4

类似前述第5阶段，i(t)处于续流状态，续流电流在桥臂中方向为自下而上，因此阻尼电阻不会被其并联的IGBT-二极管对所旁路。此时i(t)为：

(11)

对比式(9)和(11)可知，由于2Rb/3≫Req，增加阻尼电阻后可使直流断路器主支路暂态电流在此阶段的衰减速度大幅增加，从而有效减小电流持续时间T5。

4 仿真验证与分析

4.1 计算条件

为验证理论分析结果，基于PSCAD仿真平台搭建图3和图4所示的四端柔性直流电网模型，各站主要参数如表1所示。线路1—4的长度为50、210、190和220 km，各线路正负极线及金属中线同塔布置。

表1 PSCAD模型中柔性直流电网各换流站主要参数

基本计算条件为：故障前柔性直流电网无元件退出；除特殊说明外各站满功率运行；t=0时发生图4所示故障。本级直流断路器正常动作和失灵情况下，保护动作时序如前所述，具体动作时间如表2所示。

表2 保护及设备动作时间

4.2 直流断路器暂态电流特性验证

直流断路器正常动作情况下，本级直流断路器各支路暂态电流特性的仿真结果如图13所示，与3.1.2节分析一致：故障后，本级直流断路器主支路电流线性增长；接到分闸指令后，电流转入转移支路并继续增长，随后在Q2闭锁时达到峰值Ip；之后电流转入耗能支路并开始下降。

图13 直流断路器正常动作情况下暂态电流仿真结果

直流断路器失灵情况下，主支路暂态电流特性的仿真结果如图14所示，与3.2节分析一致：失灵直流断路器在故障后快速增长，在T1时刻换流器闭锁后增速变慢；在T2时刻下级直流断路器MOV投入后开始减小并出现峰值i(T2)=Ip1，在T3时刻线路1电流降为0后缓慢回升，在T4时刻出现峰值i(T4)=Ip2，随后呈指数衰减。

图14 直流断路器失灵情况下暂态电流仿真结果

4.3 柔性直流电网参数对直流断路器暂态电流影响验证

4.3.1 回路中电感值的影响

以Lp为例分析回路中电感值对直流断路器暂态电流的影响，对Lp取50、100、150、200、250、300 mH的情况进行仿真计算。本级直流断路器正常动作和失灵情况下暂态电流i(t)的仿真结果分别如图15和图16所示。Ip、Ip1、Ip2、T5随Lp的变化规律如表3所示。

图15 直流断路器正常动作时Lp取值对暂态电流影响

图16 直流断路器失灵时Lp取值对暂态电流影响

表3 Lp取值对直流断路器电流应力的影响

仿真结果显示，Lp越大则Ip、Ip1、Ip2越小。这是由于在Tb、T1、T2和T4等时间确定的条件下，Lp越大则各站子模块电容储能和交流系统能量转化为回路电感储能的速率越慢。另一方面，图16和表3显示，Lp越大则T5越大。这是由于当Lp增大，i(t)在第5阶段的衰减时间常数增大，最终导致T5增大。可见，增大回路电感值能够有效减小断路器各支路峰值(开断)电流应力Ip、Ip1和Ip2，但可能导致持续时间T5增加，与3.3节理论分析结果一致。

4.3.2 稳态电流值的影响

令各位置Lp取150 mH。通过调节各换流站有功功率，改变所观测本级直流断路器的稳态电流I0_DCB。分别对I0_DCB为2.5、1.5、0.5 kA的情况进行仿真计算。本级直流断路器正常动作和失灵情况下暂态电流i(t)的仿真结果分别如图17和图18所示。Ip、Ip1、Ip2、T5随I0_DCB变化规律如表4所示。

图17 直流断路器正常动作时I0_DCB对暂态电流影响

图18 直流断路器失灵时I0_DCB对暂态电流影响

表4 I0_DCB取值对直流断路器电流应力的影响

仿真结果显示，Ip、Ip1随初值I0_DCB等量减小，这是由于在短时间尺度Tb和T2内，di/dt保持恒定。但是，由表4可知，Ip2和T5随I0_DCB的变化微弱。这是因为在长时间尺度下i(t)中与I0_DCB有关的零输入分量已逐渐衰减到零，使得I0_DCB变化对i(t)的影响变弱。可见，减小I0_DCB能够有效减小直流断路器各支路峰值(开断)电流应力Ip、Ip1，但无法有效改善持续时间T5，与3.3节理论分析结果一致。

4.4 直流断路器暂态电流抑制方法有效性验证

对3.3节所述直流断路器主支路暂态电流抑制方法进行仿真验证，计算条件如4.1节所述。站内各桥臂上新增阻尼电阻值Rb分别取1、3、5 Ω时，本级直流断路器失灵情况下的暂态电流仿真结果如图19所示。Ip2、T5随Rb变化情况如表5所示。

图19 直流断路器失灵时Rb取值对其暂态电流的影响

表5 Rb取值对直流断路器主支路电流应力的影响

真结果表明，Rb增大可使暂态电流峰值及持续时间T5显著减小。相比于表3中未配置阻尼电阻时T5=6.33 s，当Rb为1、3、5 Ω时T5分别减小至1.05、0.41、0.27 s。这是因为一方面截止到T4时刻Rb已投入T4-T1=60 ms，使得式(11)中i(t)的衰减初值i(T4)得到抑制；另一方面，Rb增大使衰减时间常数Leq/Req也得到有效减小。上述仿真结果与3.3节理论分析结果一致，验证了电流抑制方法的有效性。

5 结 论

本文以张北工程为背景，开展柔性直流电网真实控制保护逻辑下的500 kV混合式直流断路器暂态电流特性及抑制方法研究。首先，推导了各阶段直流断路器暂态电流的计算表达式，提出了各支路暂态电流应力典型波形，揭示了直流断路器暂态电流发展规律，为直流断路器的电气设计、核心器件选型、试验方案制定提供了依据。其次，分析了柔性直流电网主回路参数对直流断路器暂态电流的影响规律。通过增大柔性直流电网回路电感和减小直流断路器稳态电流，能够在一定程度上减小断路器各支路峰值(开断)电流应力，但难以改善主支路短时电流应力持续时间。针对此问题，提出了一种基于换流站内阻尼电阻的直流断路器暂态电流抑制方法。理论分析和仿真验证结果表明，所提出方法能够有效抑制直流断路器主支路暂态电流，减小短时电流应力持续时间，从而降低了主支路器件通流能力要求，可使并联电力电子器件数量减少，有助于降低直流断路器造价、提高设备可靠性。本文的研究工作可为混合式直流断路器的设计及其在柔性直流电网中的应用奠定理论基础。