中国智能制造业绿色全要素生产率增长的时空演变
周 杰
(1.乐山师范学院 经济管理学院,四川 乐山 614000;2.广东彩艳股份有限公司博士后工作站,广东 江门 529000)
一、引言
当前,世界正面临“百年未有之大变局”,产业变革与科技革命进入全新历史节点,促使全球创新版图、经济结构重塑[1]。智能制造作为该历史节点下萌生的核心技术之一,在成功颠覆传统制造业竞争模式之余,也对全球价值链分配模式产生深远影响[2]。双碳目标导向下,绿色化成为其高质量发展的必然走向。精准把握智能制造绿色发展机遇,实现智能制造业高效与可持续发展,对中国增强本国制造业全球竞争力具有重要意义。
开展智能制造业研究是把握智能制造绿色发展机遇的重要基础。智能制造业研究最早可追溯到国外不同学派对智能制造系统组织基础与框架构建的探讨[3]。随着智能技术的快速发展,国内学者在借鉴国外研究的基础上,也对智能制造业进行了广泛而深入的探讨。详细而言,研究多围绕智能制造概念内涵[4,5]、应用领域[6,7]等内容展开,智能制造影响因素[8,9]、影响效应[10,11]也有所涉及。但囿于智能制造涵盖范围的复杂性和制造“智力”的隐含性,研究数据可得性受限,导致智能制造业全要素生产率方面的研究较为欠缺。仅有申丹虹、崔张鑫(2021)[12]以38 家智能制造业上市公司为样本,基于SFA 方法对中国2010—2018年的智能制造业全要素生产率进行了测算,并指出技术水平落后是造成观察期内智能制造业处于规模递减状态的关键原因。对上述研究进行深入诠释,可知考察智能制造业绿色全要素生产率有利于剖析智能制造高效与可持续发展着力点。综上所述,文章认为有必要对智能制造业绿色全要素生产率增长情况进行深入挖掘。
文章创新贡献表现在以下方面:第一,以2011—2020 年中国30 个省份面板数据为样本,弥补样本选择片面可能带来的偏误;第二,构建基于DEA 的Malmquist 指数模型,测度智能制造业绿色全要素生产率增长情况,尝试填补既有研究空白;第三,分解技术对智能制造业绿色全要素生产率增长的影响,探寻智能制造业绿色全要素生产率主要增长动力,拓展现有研究的宽度与广度;第四,采用核密度和马尔可夫链模型对智能制造业绿色全要素生产率增长的整体分布形态、内部动态特征及在空间的趋同效应进行分析,揭示其时空动态演变规律。
二、研究方法
1.Malmquist 指数模型
当前学术界有关全要素生产率(TFP)变化的测度方法主要分为两种,分别是参数法(索洛余值法、随机前沿函数法等)与非参数法(DEA、Malmquist 生产率指数法等)。与非参数法相比,参数法虽然能够将非效率性的影响与随机扰动区分开,但无法区分设定偏误导致的随机误差。因此,文章选用非参数法测算智能制造业绿色TFP 增长率。同时考虑到本次研究要对不同时期智能制造业绿色TFP 增长率对比分析,仅使用传统DEA模型无法满足研究需要。故而,借鉴既有研究[13-16],基于DEA理论构建了Malmquist 指数模型,测算方式如下:

式(1)中,M0表示决策单元在t 期和t+1 期的TFP 变化率,若M0大于1,表明从t 到t+1 期TFP 提高,反之则表明从t 到t+1 期TFP 降低。(xt,yt)、(xt+1,yt+1)分别为决策单元在t 期和t+1 期的投入量和产出,D0t和D0t+1分别表示以t 时期和t+1 时期为基准点的产出距离指数。
Malmquist 指数可分解为技术进步变化(TC)和技术效率变化(EC)两部分,即M0=EC×TC,二者计算公示分别如下:
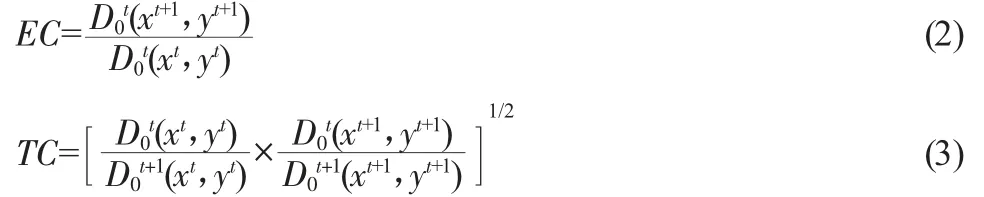
EC、TC 值大于1 表示技术效率改善或技术进步,EC、TC值小于1 表示现有技术利用未达到理想状态。
在规模效率可变情境下,EC 可进一步分解为纯技术效率变化(PE)和规模效率变化(SE),即EC=PE×SE。限于篇幅,二者计算公式不在此列示。
2.核密度模型
核密度估计是一种在给定样本集合下求解随机变量分布密度函数的非参数估计方法,能够通过平滑曲线对样本运动演变进行直观描述[17]。故而,本次研究选用核密度估计模型对智能制造业绿色全要素生产率演变态势进行分析。假设Xi为随机变量,其密度函数为f(x),则对应点x 的概率密度函数为:

上式中,N为观测值个数,Xi为独立同分布的观测值,h为平滑参数或带宽。值得注意的是,核密度估计是否准确的关键在于h(带宽)的选择,它不仅决定着核密度估计精度还决定着曲线平滑程度。h(带宽)越大,则核密度函数f(x)越光滑。K(·)为核函数,文章选用高斯核密度函数进行估计。
3.全局空间自相关分析
莫兰指数可直观描述观测对象在整个空间范围内的集聚状况[18]。文章选定莫兰指数对中国智能制造业绿色全要素生产率的全局空间自相关关系进行度量,计算公式如下:

式(5)中,I代表全局Moran's I 指数,当I>0 时,表示中国智能制造业绿色全要素生产率增长呈现空间正相关;当I<0 时,表示中国智能制造业绿色全要素生产率增长呈现空间负相关;当I=0 时,表示中国智能制造业绿色全要素生产率增长呈现空间随机分布。Wij是测度主体i 与j 的空间权重矩阵。
4.马尔可夫链模型
考虑到全局空间自相关指数仅能反映数值整体空间分布情况,无法对地区内部空间集群特征进行深入刻画,也无法直观描述空间集群时间演变历程。故此,文章构建传统马尔可夫链与空间马尔可夫链,用以研究智能制造业绿色全要素生产率增长的时空演变规律及其在空间的趋同效应。
(1)传统马尔可夫链
传统马尔可夫链在应用过程中需将智能制造业绿色全要素生产率增长指数离散为k 种类型,通过计算各类型转移概率分布以近似推断智能制造业绿色全要素生产率演变的整个过程。为获得稳健的研究结论,本次研究扩展构建基于多个年份的传统马尔可夫转移概率矩阵。矩阵元素计算公式如下:

(2)空间马尔可夫链
空间马尔科夫链是传统马尔科夫链和“空间滞后”概念结合的产物[19]。一个区域的“空间滞后”就是该区域周边地区属性值的空间加权平均,计算公式为:

式(7)中,yb为b 地区的变量数值,wab为权重矩阵W 的元素。文章采用公共边界原则确定空间权重矩阵,如下所示:

由此,空间马尔可夫转移概率矩阵将传统马尔可夫矩阵分解为k 个k×k 的条件转移概率矩阵。矩阵元素(k)表示在条件k 下,a 区域在t 年属于i 类型而在t+d 年份转移为j 类型的空间转移概率。
三、指标选取与数据来源
1.指标选取
当前学术界对智能制造业所涵盖的具体行业领域并没有统一概念,难以直接获取智能制造业发展数据。因此,文章借鉴王媛媛、张华荣(2016)[20]的研究,以自动化仪器仪表、智能控制系统、工业机器人、3D 打印设备、数控机床等智能制造细分行业综合考察智能制造业绿色发展状况。同时参考张优智、乔宇鹤(2022)[21]的研究,选取上述智能制造业细分行业销售产值总额、污染排放总量为产出指标,能源、劳动以及资本投入作为投入指标。其中,智能制造业销售产值总额需利用价格指数进行平减;污染排放总量通过“智能制造业销售产值/工业总产值×工业SO2排放量”测算;能源投入采用年末各省份智能制造业能源损耗量衡量,数据通过“智能制造业销售产值/工业总产值×工业终端能源损耗量”间接得到;劳动投入指标通过年末各省份智能制造业就业人数衡量;资本投入指标为各地区智能制造业固定资产投资额,亦需利用价格指数进行平减。
2.数据来源
2010 年《国务院关于加快培育和发展战略性新兴产业的决定》中首次提及智能制造装备概念,并将智能制造业作为长期发展重点。故而文章以2011 年作为测算智能制造业绿色全要素生产率增长基期,研究时间跨度设为2011—2020 年,样本设为30 个省份(不含西藏及港澳台地区)。与此同时,为精确刻画不同地区智能制造业绿色全要素生产率增长差异,依据国家统计局标准,将30 个省份划分为东、中、西部三大地区。研究所涉数据主要来源于历年《中国统计年鉴》 《中国工业统计年鉴》等权威数据以及各省份公布的统计报告。对于少数缺失数据,采用线性插补法予以补充。
四、实证结果与分析
1.智能制造业绿色全要素生产率测度
将各省份智能制造业相关投入产出指标数据代入Malmquist指数模型中,利用DEAP2.1 软件进行测算,结果见表1。
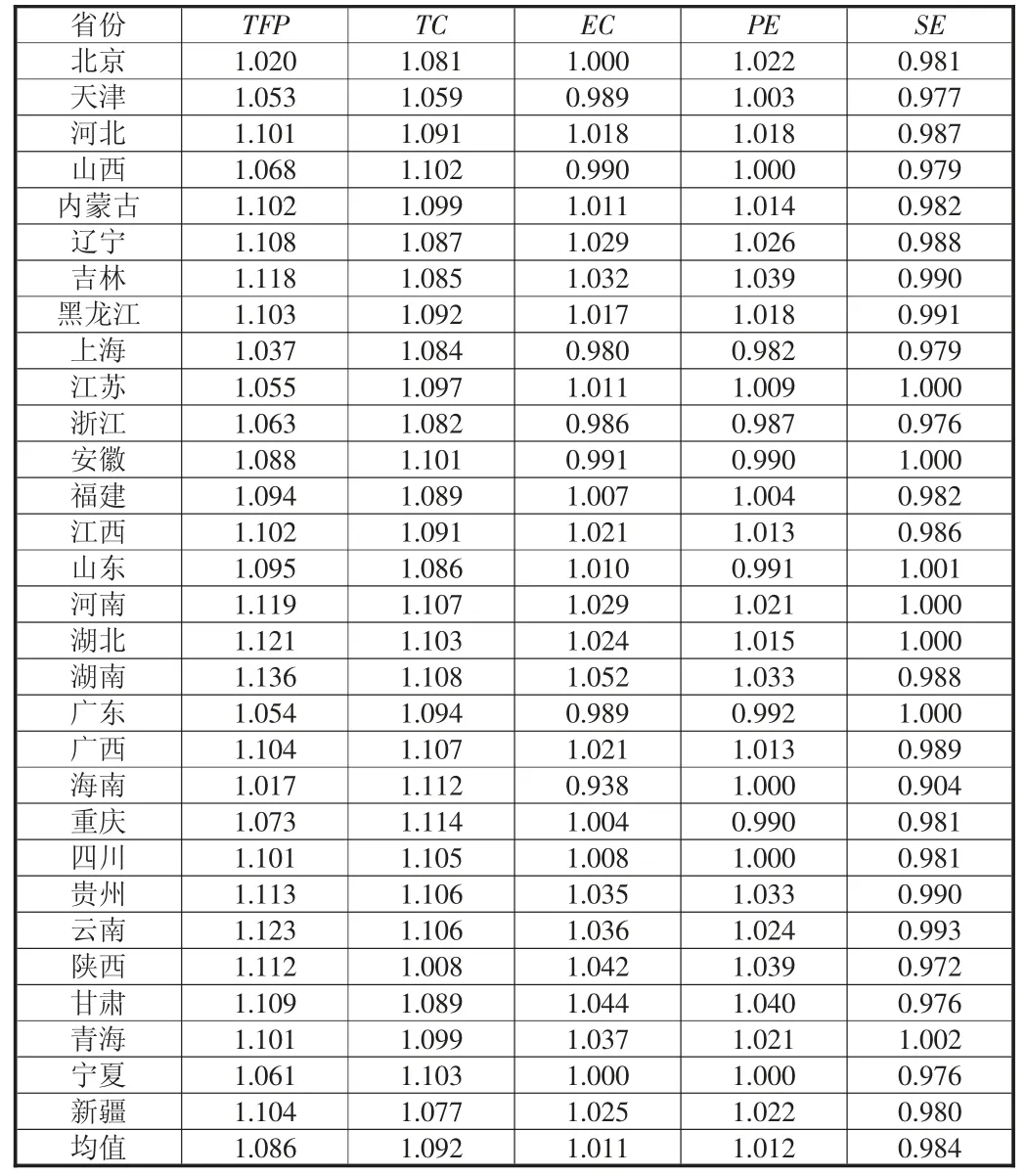
表1 2011—2020 年各省份Malmquist 指数变化及其分解
表1 中汇报了2011—2020 年中国30 个省份智能制造业Malmquist 指数及分解均值。可以发现,样本期内,30 个省份中所有省份智能制造业绿色全要素生产率均实现了正增长,其中有20 个省份的智能制造业绿色全要素生产率增长率超过了全国平均水平,包括河北、内蒙古、辽宁、吉林、湖南等省份。这表明中国智能制造业绿色全要素生产率增长态势良好。进一步分析绿色全要素生产率各内部指标的变动情况可以发现,技术进步的平均增长率为9.2%,技术效率的平均增长率为1.1%。这说明技术进步是推动智能制造业绿色全要素生产率提升的核心驱动力。就技术效率的2 个子指标而言,纯技术效率平均增长率为1.2%,而规模效率出现了负增长,平均增长率为-1.6%,这意味着纯技术效率是改善技术效率的主要推动力。
通过梳理与整合表1 数据可得2011—2020 年全国及东、中、西部地区各年份智能制造业Malmquist 指数及其分解数值。就全国层面而言,观测期内除2011 年全国智能制造业的绿色全要素生产率出现了负增长,其他年份均为正增长,平均增长率高达10.7%。这一现象说明2011 年以来,中国智能制造业发展态势整体向好,智能制造水平持续提升。进一步分析可知,2011—2020 年间中国智能制造业技术进步增长率由2.1%变为14.1%,提升了12%,而技术效率增长率由-2.6%变为-7.2%,下降了4.6%,这表明技术进步始终在智能制造业绿色全要素生产率增长过程中发挥核心驱动作用。就地区层面而言,东、中、西部三大地区智能制造业绿色全要素生产率增长速度存在差异性。2011—2020 年东部地区智能制造业绿色全要素生产率的年均增长速度为8.1%,中部地区为17.6%,西部地区为16.6%。可以发现,中、西部地区智能制造业绿色全要素生产率增长速度快于东部地区,表明近年来中、西部地区智能制造业发展更为迅猛。上述研究虽然能够较为详细地刻画智能制造业绿色全要素生产率静态分布规律,但是难以准确细致地揭示中国智能制造业动态演变收敛特征以及趋势。故而基于上述测度与分解得出的各项指标数据,进一步对智能制造业绿色全要素生产率的时空动态演变展开研究。
2.智能制造业绿色全要素生产率增长的时序动态演变分析
(1)核密度估计
文章将研究时段均等分为3 份,选取2011 年、2014 年、2017 年和2020 年的智能制造业Malmquist 指数累积值为样本,采用核密度模型估计其密度分布(见图1)。其中,坐标横轴表示智能制造业Malmquist 指数,纵轴表示核密度。
图1(a)为全国范围智能制造业Malmquist 指数的核密度曲线。由该图可知:一是智能制造业绿色全要素生产率核密度曲线均呈右偏,有较多省份智能制造业绿色全要素生产率小于全国均值;二是4 个代表年份的智能制造业绿色全要素生产率核密度曲线波峰高度不断降低,这表明全国范围内智能制造业绿色全要素生产率差距逐渐增大;三是2011 年核密度曲线由一个主峰和两个侧峰组成,2014 年两个侧峰趋于平缓,2017 年和2020 年均向单峰分布形式转变,且主波峰与次波峰间距逐年减小,表明智能制造业绿色全要素生产率演变过程中的“两极分化”效应在逐渐减缓。

图1 全国及东、中、西部地区智能制造业绿色全要素生产率核密度估计
图1(b)、(c)、(d)分别为东、中、西部地区智能制造业Malmquist 指数的核密度曲线。分析图像可以发现,东、中、西部三大地区核密度曲线具有高度相似性。其中,东部地区核密度曲线宽度逐渐变大、高度逐渐降低、尾部明显拉长。这表明东部地区各省份智能制造业绿色全要素生产率增长幅度差异增大。中部地区智能制造业Malmquist 指数的核密度曲线宽度呈现先变窄、而后逐渐变大的趋势,这表明中部地区各省份智能制造业Malmquist 指数差距在2011—2014 年间逐渐缩小,2014年以后又逐渐变大。究其原因可能在于,伴随国家对中部地方落后省份在经济、政策、技术等方面的支持力度不断加大,中部地区各省份智能制造业绿色全要素生产率增长速度得到显著提升,其内部差距逐渐缩小。西部地区智能制造业Malmquist 指数的核密度曲线波峰宽度在2011—2017 年间增大,2017 年之后无明显变化,说明2017 年之前西部地区各省份智能制造业绿色全要素生产率增长幅度具有较大差异,而在2017 年后西部地区各省份智能制造业绿色全要素生产效率增长幅度趋于均衡。
(2)马尔可夫链分析
文章以2011—2020 年中国30 个省份智能制造业Malmquist指数累积值作为样本数据,在不考虑年份差异影响的情况下,采用四分位数方法确定1.061、1.095 和1.104 为分类阈值。由此,各省份智能制造业绿色全要素生产率可分成四种水平状态,分别是低水平状态(0,1.061]、中低水平状态(1.061,1.095]、中高水平状态(1.095,1.104]、高水平状态(1.104,+∞),并依次用H、MH、ML 和L 表示。在此基础上,用传统马尔可夫链模型测算不同时长内各水平状态间的转移概率矩阵,如表2 所示。
根据表2,可具体剖析中国智能制造业绿色全要素生产率增长的时序动态演变情况。

表2 中国智能制造业绿色全要素生产率分布状态的传统马尔可夫链测算结果
第一,无论考察时长是多久,转移概率较大的数值均在矩阵对主角线上。这说明在1 年、2 年或3 年时长下,中国智能制造业绿色全要素生产率分布状态转移情况较为稳定。
第二,智能制造业绿色全要素生产率向下或者向上转移超过一种状态类型的概率偏低,即智能制造业绿色全要素生产率难以跨状态转移。具体来说,仅有考察时长为3 年时,中国智能制造业绿色全要素生产率分布状态存在跨状态转移,表现为低水平状态向中高水平状态转移,转移概率为1.1%。
第三,在期初智能制造业绿色全要素生产率是高水平状态的省份,1 年后依然处于原状态的概率是96.7%,2 年后是96.8%,3 年后是97.5%。而低水平状态省份经过发展后,依然处于原状态的概率分别为72.3%、71.7%、69.5%。可见,智能制造业绿色全要素生产率增长的动态演进过程存在一定两极分化现象,即强者越强,弱者越弱。
第四,当考察时长为1 年时,L、ML 和MH 向上转移的概率分别是27.7%、15.8%和7.2%。当考察时长为2 年时,L、ML 和MH 向上转移的概率分别是28.3%、19.1%、8.5%。当考察时长为3 年时,L、ML 和MH 向上转移的概率分别是30.5%、21.6%和9.1%。可见,考察时长越长,偏低水平状态的省份向上转移概率越大。
3.智能制造业绿色全要素生产率增长的空间格局演变分析
(1)全局空间自相关分析
若想探究智能制造业绿色全要素生产率增长幅度在空间层面的动态演进特征,需先研判其全局空间自相关性。将智能制造业Malmquist 指数的各项指标代入式(5)中,得到各年份智能制造业绿色全要素生产率增长的全局莫兰指数(见表3)。
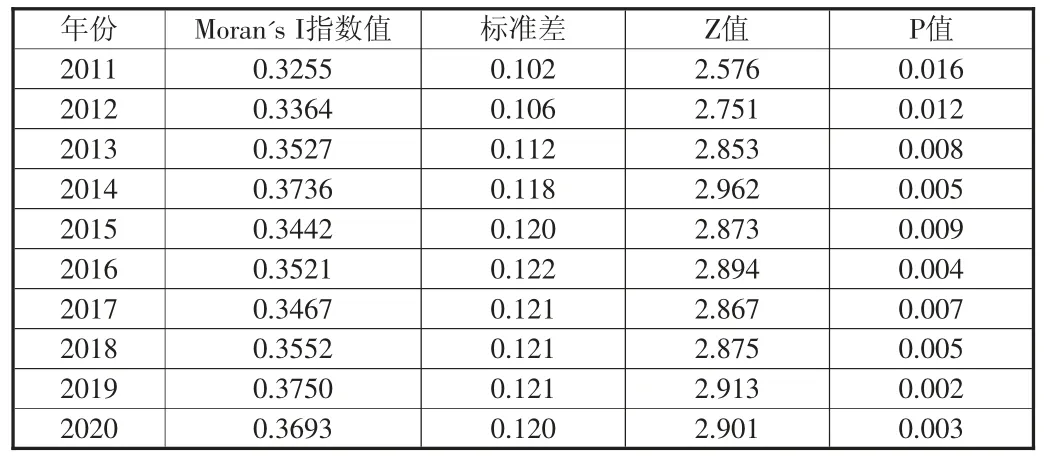
表3 智能制造业全要素生产率的Moran's I 指数值及其相关统计指标
如表3 所示,研究期内Moran's I 指数值均大于零,并且除前2 年P 值显示仅通过5%的显著性检验外,其余观测年份都在1%上显著。这说明从空间分布来看,智能制造业绿色全要素生产率增长会出现明显的相似水平空间集聚现象。另外,2011—2020 年中国智能制造业绿色全要素生产率增长的空间格局演变大致可划分为两个阶段:第一阶段为2011—2014 年,该阶段智能制造业绿色全要素生产率的Moran's I 指数值呈现平稳上升趋势,各省份间集聚水平逐步强化;第二阶段为2015—2020 年,该阶段Moran's I 指数值“下降、上升”趋势不断交替演变,各省份的智能制造业绿色全要素生产率增长的空间集聚效应波动不断增强。综合来看,各省份空间自相关性在考察期内持续增强。
(2)空间马尔可夫链分析
空间自相关分析表明,中国智能制造业绿色全要素生产率增长呈现出显著的空间自相关性,即某地区智能制造业绿色全要素增长受到相邻地区绿色全要素生产率水平影响。文章将进一步探究这种影响如何对智能制造业绿色全要素生产率增长的动态演变产生作用。文章将空间滞后条件设定为相邻地区智能制造业绿色全要素生产率增长水平,并以此搭建空间马尔可夫链转移概率矩阵(表4)。

表4 空间马尔可夫链转移概率矩阵
由表4 可知,空间滞后类型对智能制造业绿色全要素生产率演变有重要影响,不同空间滞后类型对不同分布状态下智能制造业绿色全要素生产率转移概率的影响各不相同。具体表现为:
第一,对于低水平状态省份来说,在不考虑空间作用时,这些地区有27.7%的概率由低水平状态往上转移;在考虑空间作用且面临低、中低、中高和高水平状态邻居时,这些地区分别有38.4%、45.5%、48.1%、0%的概率往上转移。可见,前三类状态邻居均提升了低水平状态省份往上转移的概率,而高水平状态邻居则具有负面影响。
第二,对于中低水平状态省份来说,在不考虑空间作用时,这些地区有15.8%的概率由中低水平状态往上转移;在考虑空间作用且由低到高面临四类状态邻居时,这些地区有17.3%、23.2%、35.7%和37.6%的概率由中低水平状态往上转移。可见,在四种空间滞后类型影响下,中低水平状态地区智能制造业绿色全要素生产率增长向上转移的概率均有所增加。
第三,对于中高水平状态省份来说,在不考虑空间作用时,这些地区有7.2%的概率由中高水平状态往上转移;在考虑空间作用且由低到高面临四类状态邻居时,这些地区有5.2%、8.3%、8.6%和9.1%的概率由中高水平状态往上转移。可见,对于中高水平状态的省份来说,面临中低、中高与高水平状态邻居时可增大向上转移概率,面临低水平状态邻居时会降低向上转移概率。
第四,对于高水平状态省份来说,在不考虑空间作用时,这些地区有3.3%的概率由高水平状态往下转移;在考虑空间作用且由低到高面临四类状态邻居时,这些地区有6.8%、0、0、0 的概率由高水平状态往下转移。可见,当高水平状态的省份面临高水平状态邻居时,容易发生恶性竞争,进而增加往下转移的概率。
五、结论与建议
文章采用基于DEA 的Malmquist 指数模型对中国各省份智能制造业绿色全要素生产率变化情况及其分解进行测度,并通过核密度与马尔可夫链分析中国智能制造业绿色全要素生产率增长的时空演变规律。结果显示:一是考察期内中国各省份的智能制造业绿色全要素生产率整体呈现上升态势,推动中国智能制造业绿色全要素生产率增长的核心驱动力是技术进步;二是各代表年份智能制造业绿色全要素生产率的核密度曲线出现了不同程度的右偏态势,且随时间不断推移,波峰高度不断降低;三是中国智能制造业绿色全要素生产率分布状态具有一定的稳定性,即跨状态转移概率不高。通过增加考察时长发现,智能制造业绿色全要素生产率增长的动态演变呈现出两极分化现象,即“强者越强、弱者越弱”,且处于较低水平状态的省份转移到更高级别发展状态的概率有所增加;四是不同空间滞后类型对不同状态下智能制造业绿色全要素生产率转移概率的影响各不相同。
基于以上结论,提出如下针对性建议:第一,培育“绿碳”优势智能制造业集群。智能制造业发达的东部地区应与周边地区联合组建产业集群,以点带面增强区域智能制造业绿色全要素生产率,发挥规模化发展的正向促进效应。中部地区应结合本地区资源、社会现实情况,以“绿碳”为导向升级智能制造业结构,进而改善智能制造业绿色全要素生产率。西部地区应加大智能制造业集群规模,积极承接其他地区的智能制造业转移,持续提升低碳智能产品开发能力、生产制造能力与综合管理能力。第二,加强智能制造业“绿碳”技术竞争力。智能制造业应以升级“绿碳”技术为关键突破口,大力发展新一代信息技术、生物安全等战略性新兴产业,进一步提高智能制造业的低碳化管理与生产效率。政府应鼓励智能制造企业积极研发新型“绿碳”技术,及时发布技术突破引导政策,推动先进管理方式与技术研发流程对智能制造业绿色全要素生产率增长作出贡献。各状态等级地区均应重视引入和吸收前沿“绿碳”技术,加快将技术优势转变为智能制造业绿色发展动能。第三,打造智能制造业“绿色品牌”领军企业。各地区应根植于本地市场基本情况,快速打造出具有本土特色的智能制造业“绿色品牌”领军企业,再引导其辐射带动周边地区智能制造业企业“绿色品牌”发展,形成区域“绿色品牌”规模化发展态势,为智能制造业绿色发展贡献力量。同时,各地区应加速智能制造业“绿色品牌”领军企业之间的资源循环流动速度,提升“绿色品牌”要素配置效率,最大化发挥领军企业的辐射带动作用。

