基于工作点在线计算的双馈机组网侧变流器高电压穿越控制
王耀函,张扬帆,宋 鹏,刘 辉,吴林林,张瑞芳
(风光储并网运行技术国家电网公司重点实验室(国网冀北电力有限公司电力科学研究院),北京 100045)
近年来,随着风力发电系统的广泛应用和并网装机容量的不断增加,其在电网故障条件下的运行与控制策略已直接影响到电力系统的安全稳定运行[1-2]。电网电压骤升是一种常见的电网故障,通常发生在电网无功功率过剩的情况下[3]。电网电压发生跌落时,无功补偿设备会发出无功功率,在电网电压恢复过程中可能因为所投入的电容补偿器不能及时退出而引发电网电压的骤升。为了避免风电机组因暂态过电压而脱网,有必要对风电机组的高电压穿越HVRT(high voltage ride through)控制策略进行研究。
电网电压正常时,风电变流器运行于正常控制模式,而电网电压发生跌落或者抬升故障后,变流器需要切换至暂态运行模式,不同状态之间的切换依赖于对电网电压的检测。因此,电压快速精确检测是提升风电机组HVRT过程中响应速度的关键环节。常用的电压检测方法有峰值电压法、有效值法、小波变换法、卡尔曼滤波法、dq变换法等。文献[4]利用dq变换,通过低通滤波器提取正序分量,再由dq反变换后得到的量与原输入量相减得到补偿电压量,但这种方法不区分正负序分量和谐波分量,某些谐波分量的引入会导致系统不稳定。文献[5]通过构造形态滤波器提取三相电压经dq变化后的直流分量,并基于自适应最小均方滤波器提升锁相环精度,但是很大程度上增加了算法复杂度。最小方差LES(least error squares)滤波器可以将直流分量、各次谐波分量及基波分量快速地提取出来,便于后期的数字化分析和处理,目前较多用于动态电压恢复器DVR(dynamic voltage regulator)的电网电压幅值检测中[6]。
针对电网电压骤升,我国提出了风电机组HVRT 要求,即在电网电压骤升至1.3 倍标称值以内,不仅要求风力发电机组必须能不脱网持续运行一段时间,而且在故障期间要求其对电网有一定的动态无功支撑。文献[7]针对传统PI 控制器带宽和动态响应性能的不足,引入PI-R控制器有效抑制骤升故障下的转子电流冲击。文献[8]从双馈风力发电机组暂态过程出发,考虑HVRT过程中切换延时和无功控制因素的影响,优化转子侧电流表达式,设计了一种有效抑制转子过流的控制策略。现有控制策略大多是从转子侧出发,但是电网电压骤升会带来变流器网侧的控制裕度下降[9-10],若失控则会导致能量由电网倒灌进入逆变器进而引发直流侧过压或过流。电网电压骤升时,网侧变流器安全运行区域缩小,需快速抑制网侧过调制引起的电压、电流冲击,通过增加感性无功电流输出或提升直流母线电压参考值可以增加变流器控制裕度[11]。对于给定容量的变流器如何满足风电机组HVRT 测试对动态无功电流的要求,以及网侧无功电流与直流母线电压配合还需要进一步分析。
为提高双馈风电机组在HVRT 过程中的响应速度及稳态控制效果,本文针对双馈网侧变流器设计HVRT 控制策略。首先采用LES 滤波器检测电网电压幅值并给出参数设计方案。其次建立变流器网侧数学模型,由变流器电压和电流约束关系,确定其在不同电网电压骤升幅度情况下的安全运行区域。在此基础上,在线计算HVRT稳态最佳工作点,使变流器网侧无功电流和直流母线电压参考值按照一定速率提升至最佳工作点。通过双闭环矢量控制方式,使得实际的直流母线电压和无功电流跟踪其给定的参考值。最后,仿真结果表明,所提出的网侧控制策略能够提高风电机组在故障穿越期间的响应速度及稳态控制效果。
1 LES 滤波器参数设计
本文采用LES 滤波器实现对电网电压快速精确检测。LES滤波器对电网电压瞬时值u(t)连续N次采样结果,可以快速提取出其基波分量的幅值[6]。LES 滤波器具有4 个控制参数:采样窗长度N、采样周期Ts、本次采样对应的具体时间t0、被提取信号角频率ω。由于仅需提取基波信号,设ω=100π。由于t0取值只影响信号相位,不影响信号幅值,t0可设为任意值,为了简化运算,这里设t0=0 。因此,LES 滤波器的可调控制参数仅有2个,即N和Ts。
首先,N和Ts存在理论最值。根据“采样定理”可知,若要实现对基波频率的完整复现,则采样频率至少为基波频率的2 倍,一般取10 倍以上,因此Ts存在最大值,即Ts≤1/(500 Hz)=2 ms。其次,N和Ts的乘积决定LES 滤波器的滤波效果和响应速度。LES滤波器的响应时间为(N+1)Ts。若将LES滤波器近似等效为一阶低通滤波器,则可估算其截止频率近似为1/[(N+1)Ts]。
在具体参数设计时,首先考虑到电网电压变化时LES滤波器应快速检测其幅值变化,响应时间不宜过长,一般在半周波内。其次,考虑到电网中会含有5、7 次谐波扰动,截止频率不宜过高,一般使其小于250 Hz。因此,设计LES滤波器响应时间在4~6 ms之间,约为1/4周波,同时应让采样窗口在合理范围内,以减轻控制器计算负担,设计采样窗口长度小于20。

表1 典型LES 滤波器参数设计Tab.1 Parameter design of typical LES filter
LES 滤波器的响应速度与滤波效果不可兼得,在参数设计时,需要根据实际工况特点,估计响应时间和截止频率范围,再结合该范围与采样频率来计算采样窗长度,完成整体设计。
2 网侧变流器安全运行区域
电网电压骤升对双馈变流器网侧和转子侧均会产生影响。其中,对网侧的影响主要是电网电压较大时,违背了升压电路原理,导致网侧控制失败;对转子侧的影响主要与低压穿越类似,在定、转子磁链中产生暂态衰减分量,引起转子过流、直流母线电压过压。本文主要针对电网电压升高引起的网侧过调制问题,通过分析电流电压约束条件,设计基于工作点计算的网侧控制策略,下面对双馈变流器网侧约束条件及安全运行区域进行详细分析。
双馈风力发电系统采用两个背靠背的变流器通过直流环节连接进行交流励磁[12]。网侧变流器及各控制变量如图1所示。
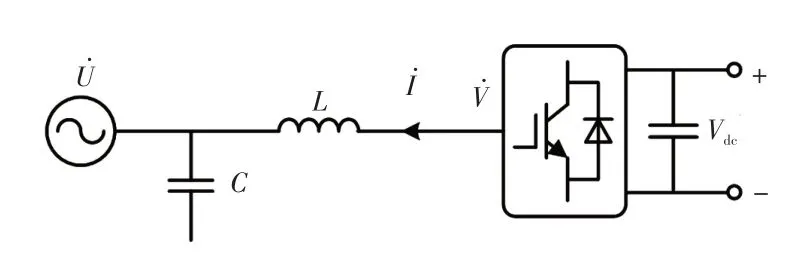
图1 网侧变流器模型Fig.1 Model of grid-side converter
图1 中,为电网相电压矢量;为网侧变流器出口相电压矢量;L为网侧变流器滤波电感;C为网侧变流器滤波电容;为变流器出口电流矢量;Vdc为网侧控制时的直流母线电压。在以定向的dq旋转坐标系下,各矢量可表示为

式中:Vd、Vq分别为网侧变流器出口相电压矢量的d、q轴分量;Id、Iq分别为变流器出口电流矢量的d、q轴分量;Ud、Uq分别为电网相电压矢量的d、q轴分量;为电网相电压矢量幅值。
根据图1,各电压、电流矢量存在如下关系:

式中,ω为电网角频率。将式(1)代入式(2)可得

由于变流器电流不可超过其最大允许电流Imax,因此存在电流约束条件,即

根据空间矢量调制原理,直流母线电压应不低于逆变器出口线电压峰值,否则会出现过调制现象,因此存在电压约束条件,即

将式(3)代入式(5)可得

将式(6)整理为

由于有功电流Iq对过调制影响较小,因此可以忽略不计。在不平衡条件下,电网线电压矢量旋转轨迹为椭圆,其幅值中含有2倍频波动,不利于控制系统稳定,因此用三路瞬时线电压幅值的最大值UL_max代替。由于UL_max恒大于|,因此不等式条件仍然成立。式(7)可简化为

可见,式(8)将电压约束条件化简为1条边界线。
建立Id Vdc直角坐标系,根据式(8)绘制不同UL_max下的边界线,如图2所示。规定直流母线电压工作范围为[1 070 V,1 150 V],无功电流工作范围为[0 A,450 A]。因此,在图2中阴影区域为网侧变流器的安全工作区。

图2 安全工作区域示意Fig.2 Schematic of safe operation area
3 HVRT 稳态最佳工作点计算
前文已经确定了不同电网电压条件下HVRT期间网侧变流器的安全运行区域,需在安全工作区内寻找使得HVRT 过调制时间最短且稳态波动小的最佳工作点。
当电网电压正常时,网侧变流器工作点为(0 A,1 070 V)。根据式(8),在电网电压抬升后,工作点必须进入阴影区域内,否则会发生过调制,即HVRT期间直流母线电压抬升的同时网侧发出无功。由图2 可以看出,若工作点位于电压极限边界线上,则可获得最高直流母线电压与无功电流利用率。从正常工作点至电压极限边界线的路径有无数条,在实际中希望能在最短的时间内抑制HVRT 引起的过调制问题,因此最优行进路径应为使工作点移动时间最短且HVRT稳态波动小的曲线。
为保持系统稳定、实现超调抑制,设计了1 组电压、电流斜坡限制器,所限制的最大斜率值分别为dV和dI。在参数设计时,dV和dI应低于电压外环和电流内环的响应速度,否则斜坡限制器无意义。因此,在电网电压骤升后,若Vdc和Id可较好地跟踪其参考值,则Vdc将以dV速度增长,Id将以dI速度增长,可表示为

将式(9)消去时间t可得

将式(10)称为强制行进线方程,即由于Vdc和Id的增长速度固定。在电网电压骤升后,工作点的移动路径不是任意的,而是必须沿着式(10)行进。根据式(10)绘制行进曲线如图3所示。

图3 行进曲线示意Fig.3 Schematic of route curve
图3中,在边界线上设计了3个工作点,分别为强制行进线和边界线交点、交点以上任意点及交点以下任意点。若工作点为强制行进线和边界线交点,则移动路径将一直在强制行进线上,此时Vdc和Id将同时升至HVRT 所需的电压及电流值,因此用时最短。若工作点在交点以下,则移动路径为先沿强制行进线移动,直至Vdc达到电压要求值,然后水平移动直至Id达到电流要求,其路径为折线,用时要明显长于最佳工作点。同理,若工作点在交点以上,用时也长于最佳工作点。由此可见,为保证HVRT 过调制时间最短且稳态波动小,最佳工作点应为强制行进线与边界线的交点。联立式(10)和式(8)可得出电流、电压最佳工作点为


图4 网侧HVRT 控制系统结构Fig.4 Structure of grid-side HVRT control system
图4 中参数补偿模块的主要功能为补偿由电感参数不准确引起的最佳工作点误差,当最佳工作点落在安全区域外时,补偿相应电压和电流,防止过调制发生。可见,PI补偿模块的主要目的不是为了实现快速响应,而是为了消除稳态误差,实现精确闭环控制。参数补偿模块由滞环控制器、无功电流PI控制器和直流母线电压PI控制器组成。
滞环控制器主要功能首先是防止HVRT 发生前PI 控制器工作于负限幅区。根据图3 的控制结构可以看出,当电网电压正常时,其线电压幅值约为976 V,与直流母线电压(约为1 070 V)存在约-94 V 的压差,导致两PI 控制器工作于负限幅区。若在此工况下发生HVRT,则积分器需从负限幅值开始累积,降低了PI 控制器的效能。其次,防止非HVRT 情况下,PI 控制器误动作,当负载波动时,可能会出现短时过调制现象,此时HVRT 控制器不应动作。
因此,设计滞环控制器对两个PI控制器进行必要的使能或清零操作。当HVRT发生时,开启PI控制器,使其从0 开始累加;在HVRT 结束后,关闭PI控制器,同时对积分器清零,为下次HVRT 做准备。根据上述原理,设计滞环上限为0,环宽范围为0~94 V。环宽过小会造成PI控制器频繁投切,不利于系统控制;环宽过大会增加滞环控制的盲区,HVRT后电压回落在环宽范围内时,仍会使PI控制器工作于负限幅区,导致滞环控制功能失效。
无功电流PI 控制器和直流母线电压PI 控制器输入为UL_max与Vdc的差值加上静态补偿量B。静态补偿量B是为了使HVRT 稳态期间UL_max略高于Vdc。对于比例系数kpI和积分系数kiI,可根据电流环数学模型进行整定。
绘制无功电流环闭环控制框图如图5 所示。图5中,GI(s)为网侧控制的无功电流内环的等效模型,由于电流内环可近似为一阶惯性环节,且响应时间约为0.001 s,因此可认为GI(s)=1/[(0.001/3)s+1]。由图5 可以看出,无功电流PI 控制器通过调节Id,使VL_max向Vdc移动,进而消除稳态误差。
将图5中的B、UL_max和视为扰动量,建立系统闭环传递函数模型为

图5 HVRT 控制系统电流环闭环框图Fig.5 Block diagram of current closed-loop of HVRT control system

通过调整PI 参数可使式(13)等效为一阶惯性环节,即

式中,tr为整定后的无功电流环调节时间。
联立式(13)和式(14)可得kpI和kiI为

PI控制器主要负责稳态补偿,不要求过快的影响速度,因此设计tr在4~10周波之间即可。
4 仿真验证
对所提HVRT控制策略进行仿真验证,系统执行频率为5 kHz,脉宽调制周期为2.5 kHz。仿真模型中采用1.5 MW 的双馈异步电机并配备变流器,网侧变流器相关参数如表2所示。

表2 双馈机组网侧变流器参数Tab.2 Parameters of grid-side converter in doubly-fed wind turbine
在图6中,设t=1.0 s前电网电压为额定值,t=1.0 s 时三相电网电压平衡骤升至1.2 倍,网侧控制系统未加入HVRT策略,即网侧无功电流和直流母线电压的参考值保持不变。图6展示了电网故障前后网侧变流器出口相电流、线电压及直流母线电压的波形,其中ia、ib、ic分别为网侧三相瞬时电流。可以看出,电压抬升后网侧变流器出现严重的过调制现象,网侧电流严重畸变且直流母线电压出现抖动。
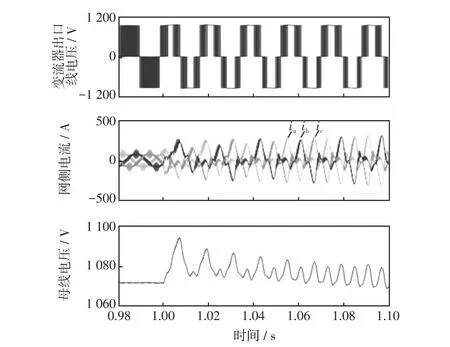
图6 无HVRT 控制策略时仿真波形Fig.6 Simulation waveforms without HVRT control strategy
网侧加入HVRT控制策略后的仿真结果如图7所示。t=1.0 s 时三相电网电压平衡骤升至1.2 倍。可以看出,加入HVRT 控制策略后,过调制现象得到抑制,网侧电流正弦度良好,直流母线电压无抖动,且由过调制引起的直流母线电压冲击也得到抑制。图7对比了选取不同HVRT工作点时的控制效果,对最佳工作点和最优行进原理的有效性进行验证。图7(b)根据式(11)和式(12)计算最佳工作点为(180 A,1 122 V),图7(a)未选取最佳工作点,而是选取边界线上任意点为(260 A,1 090 V),图7(a)和图7(b)其他控制参数完全一致。对比可以看出,当HVRT 工作点选为最佳工作点时,过调制在1 周波内得到有效抑制;当不为最佳工作点时,过调制时间加长,由此证明本文所提控制策略的有效性。

图7 采取HVRT 控制策略时仿真波形Fig.7 Simulation waveforms under HVRT control strategy
虽然上述两种组合都能够满足1.2倍HVRT运行,但是选取非最佳工作点时直流母线电压较低,网侧电流过大已接近变流器上限;选取最佳工作点时直流母线电压Vdc和无功电流Id都能够在合理范围内并留有一定的裕量,这对于变流器的运行是有利的。
在确定HVRT 期间工作点的最优行进路线时,为保持系统稳定、实现超调抑制,设计了直流母线电压、无功电流电流斜坡限制器,对斜坡限制器的效果进行仿真验证,选取相同的工作点(180 A,1 125 V),对比电压和电流参考值以阶跃形式给定和斜坡形式给定的仿真效果。电压和电流均不加斜坡限制(以阶跃形式给定参考值)时网侧电流和直流母线电压仿真结果如图8(a)所示,可以看出,进入HVRT时网侧电流和直流母线电压均存在1个较大的冲击,该冲击有可能超过变流器的安全运行范围,造成变流器故障停机。同时在HVRT期间网侧电流和直流母线电压波动较大,影响变流器的正常运行,并造成电网电压波动。电压和电流加入斜坡限制时网侧电流和直流母线电压仿真结果如图8(b)所示,可以看出,HVRT 进入瞬间和HVRT 期间网侧电流和直流母线电压均较稳定。
对比图8(a)和图8(b)仿真结果可以发现,加入斜坡限制时电流、电压冲击及稳态波动都能够得到很好的抑制,由于直流母线电压和网侧电流均与电网电压相关,当电压和电流给定过快时容易导致发生过压或过流及稳态波动。

图8 工作点移动路径的斜坡限制器仿真效果验证Fig.8 Verification of simulation effects of slope limiter for moving route of operating point
下面验证PI 补偿模块对系统HVRT 稳态工作点误差的补偿作用。仿真中,三相电网电压于t=1.0 s 时平衡骤升至1.2 倍,采用本文所提出的网侧HVRT 控制策略,且加入参数补偿模块,HVRT 工作点仍为(180 A,1 125 V)。由图9 可以看出,t=1.00~1.04 s时,控制系统的输出与工作点计算值之间存在误差,这主要是由电感误差和静态补偿量B引起。经过PI 参数补偿模块的作用,误差逐渐缩小,t=1.04 s之后,位于最佳工作点计算值附近。由此可见,参数补偿模块可以消除HVRT稳态工作点的误差。

图9 电网电压骤升至1.2 倍时控制系统的输出波形Fig.9 Output waveforms of control system when grid voltage suddenly rises to 1.2 times its original value
5 结语
为提升双馈风电机组在HVRT 期间的响应速度和稳态控制效果,首先,本文采用LES 滤波器实现电网电压幅值快速精确检测并给出其参数设计方案;其次,根据网侧变流器数学模型确定双馈风电机组在不同电网电压条件下的最佳工作点,使变流器网侧无功电流和直流母线电压按照最优行进路径运行至最优工作点,并通过参数补偿模块消除由电感等参数不准确引起的最佳工作点误差;最后,仿真结果表明,所提的优化控制策略能够提高风电机组在HVRT 期间的响应速度及稳态控制效果,具有响应速度快、稳态波动小、资源利用率高、状态切换平滑等优点。

