水平气井气液两相管流压降预测
罗程程,吴宁,王华,刘永辉,张腾,王本强,吴朋勃,刘军
1)西南石油大学油气藏地质及开发工程国家重点实验室,四川成都 610500;2)川庆钻探工程有限公司页岩气勘探开发项目经理部,四川成都 610051;3)中国石化西南油气分公司采气四厂,重庆 402160;4)中国石油西南油气田公司页岩气研究院,四川成都610051
准确预测气井气液两相管流压降对气井的生产优化和动态分析至关重要,也是准确进行排水采气工艺设计的关键参数之一[1].当天然气从储层中产出后,水和凝析油通常也会随之产出,导致井筒中出现多相流.由于井筒多相流复杂的流动特性,管道尺寸、流体性质和倾角等许多参数对压力降都有显著影响.目前,尚无在较宽的气液范围内均能保持良好预测能力的压降模型.
作为气液两相流中极为重要的参数,学者们通过广泛的实验和理论研究提出了一系列的预测模型,这些模型主要分为2 大类:①以Duns-Ros 模型[2]为代表的经验模型,该方法基于大量中低压实验数据拟合建立,拟合精度与实验数据点范围权重相关.目前模型大多基于油井生产参数范围所建,偏向低气液比条件,而在具有高气液比和低产液特征的气井中,模型精度难以保证.此外,还需选用合理准数来表征低压实验与高压气井的流动相似性,以消除低压实验和高压气井巨大的流动差异.②基于流体之间力平衡分析而建立的机理模型[3].尽管该类模型应用更广泛,但大量现场实践表明,机理模型运用效果远不如经验模型[4-5].究其原因,气井井筒流动规律较为复杂,尤其是在搅动流时,复杂的振荡流动特性使其难以建模,只能采用插值或者简化为段塞流来处理和建模,大量简化的气液界面特性(如液膜型态和湿周等)会导致模型准确性降低.
基于流型转变界限,本研究提出一种简单的持液率模型,并通过文献及现场生产测压数据对模型的适用范围和精度进行验证.
1 气井气液两相管流压降方程
对于稳定的气液两相流动而言,压力降由重力项、摩阻项和加速度项组成,表达式为
其中,p为压力,单位:Pa;z为管道或井筒长度,单位:m;ρm为两相混合密度,单位:kg/m3;g为重力加速度,单位:m/s2;θ为管道/井筒与水平方向的夹角,单位:°;f为摩阻系数;vm为气液混合物表观速度,单位:m/s;D为管道直径,单位:m;vSG为气相表观流速,单位:m/s.
混合密度是关于持液率的函数,为

其中,HL为持液率,单位:%;ρL为液体密度,单位:kg/m3;ρG为气体密度,单位:kg/m3.
由式(1)和式(2)可知,计算井筒压力降的关键是准确预测持液率及摩阻系数.在环状流时,井筒持液率低,流动规律稳定,井筒流体压降预测相对准确.而在非环状流时,井筒中摩擦阻力占比非常小.近年来,部分研究甚至在实验中观测到管壁对液膜的摩擦阻力向上的情况,这是由于管壁液膜反转后摩擦力反而提供支撑力所造成的[6].因此,气井井筒流体压降研究的核心为持液率的准确预测.本研究中摩擦阻力采用Mukherjee &Brill 模型[7]进行计算.
2 垂直管持液率模型
2.1 持液率模型的构建
相同条件下,随着气流速的增加,井筒持液率会逐渐降低.在这一变化过程中,尽管井筒流型会逐渐从泡状流发展到环状流,但大量实验和理论研究表明,持液率随气流速变化会呈现光滑的曲线[2,7-9].实际上,工程常用的经典模型中,也是采用特定类型的曲线来表征持液率随气流速的变化规律的:未划分流型的Mukherjee &Brill 模型[7]和适用于中高产气井的Gray模型[8]均采用了指数形式的曲线来表征持液率随气流速等参数的变化;而划分流型的模型,如Beggs&Brill 模型[9]和Duns-Ros 模型[2]等,在划分的流型内也利用实验数据拟合了幂指数形式的持液率模型.因此,采用某一特定曲线方程能够表征持液率随气流速的变化规律.
现有工程经典模型在给定曲线类型后,利用大量实验数据拟合相关参数,进而对持液率进行预测.而基于现有模型单因素分析持液率随气流速变化趋势,不同流动参数(如液流速和管径等)下可得到不同轨迹的曲线.反之,当其他流动参数确定时,曲线就是唯一的.通过两点对应参数即可确定指数、对数或幂率式等曲线(图1).图1 显示,不同曲线的持液率随气流速变化的速率并不同,如果采用第3个点,则可以明确曲线的曲率.因此,在其他参数一定时,只需要3个点对应的持液率及气流速就可以建立持液率随气流速的变化趋势,3个点则可以采用流型转变点(环状-搅动、搅动-段塞和段塞-泡状流转变点)进行计算.模型完全不需要实验数据拟合,而流型转变点则依托于机理或者半经验模型求解,因此模型不受实验参数范围的影响,属于半经验模型,具有良好的应用前景.
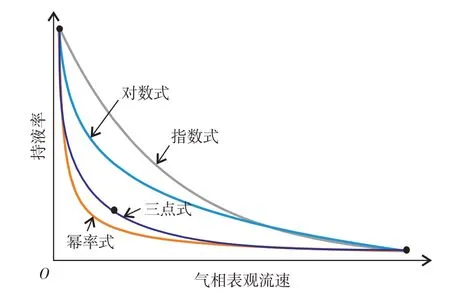
图1 气流速-持液率变化曲线Fig.1 Gas velocity-liquid holdup curves of exponential type(gray line),logarithmic type(light blue line),three-point type(dark blue line),and power-law type(orange line).
本研究构建3点曲线表征持液率随气流速的变化表达式为

其中,A、B和C均为模型系数.
由式(3)可知,当系数A、B和C确定时,即可明确持液率随气相表观流速的变化趋势,进而预测不同气流速下的持液率.
2.2 流型转变点预测模型
气井通常具有高气液比的特征,在绝大部分气井的产液范围内不同气流速下能依次出现环状-搅动、搅动-段塞和段塞-泡状流型转变点.不同转变点的计算方法如下.
2.2.1 环状-搅动流转变点
液膜反转可作为环状-搅动流的转变界限.图2为不同气流速下液膜的受力分析,τi和τw分别为相界面切应力和管壁切应力.由图2可见,随着气流速降低,气芯提供拖曳力逐渐减小,从而导致液膜变厚和管壁摩擦阻力减小,当降低到某一界限值时,会使得管壁液膜摩阻为0,此时液膜重力与气芯拖曳力相等,进一步降低气流速会导致液膜出现反转,管壁对液膜提供向上的摩擦支撑力.因此,当摩阻为0时,气芯拖曳力与重力相等是求解液膜反转气流速的边界条件.
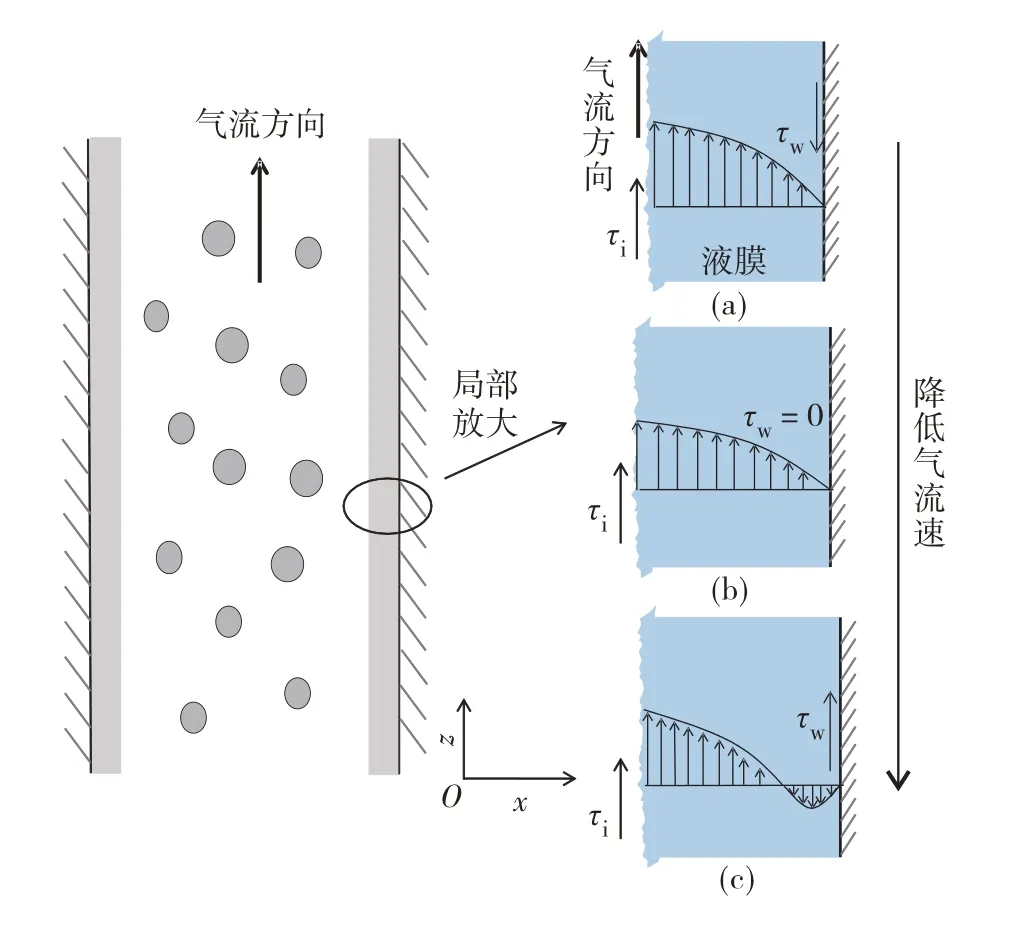
图2 垂直管道中液膜反转示意图Fig.2 Schematic diagram of liquid film reversal in vertical pipes,in which(a),(b)and(c)are enlarged parts with different τw.
为对管壁液膜进行求解,首先需要对其液膜流动进行一些假设和简化[10]:①液膜稳定流动且为层流;②液体为不可压缩的牛顿流体;③油管周向位置液膜厚度相等;④液膜为纯液体,未夹带气泡;⑤忽略液膜-气芯的波动,即气液界面为直线.
基于两相流中液膜沿着周向的分布情况,首先建立液膜的柱面坐标系,如图3所示.对于垂直管中的液膜,与液膜重力相比,压力梯度可忽略,因此Navier-Stokes方程可简化为

图3 液膜受力分析示意图Fig.3 Schematic diagram of force analysis of liquid film.

其中,r为截面半径,单位:m;vz为液膜速度,单位:m/s;μL为液相黏度,单位:Pa·s.
当液膜反转时,管壁摩阻为0且液膜速度为0.因此,边界条件为
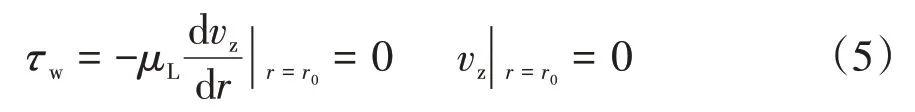
其中,τw为管壁切应力,单位:Pa;r0为油管半径,单位:m.
液膜所受气相剪切应力为

其中,τi为相界面切应力,单位:Pa;δ为液膜厚度,单位:m.
由式(4)和式(5)可得到液膜的径向速度,对其积分可得对应的液膜流量Qf为

根据式(7)可得液膜厚度的计算公式为

环状流时,液体以贴附于管壁的液膜和夹带于气芯中的液滴两种形式向上携带,因此,液膜流量为

其中,QL为进液量,单位:m3/s;fE为液滴夹带率,可采用SAWANT等[11]提出的经验关系式进行计算.
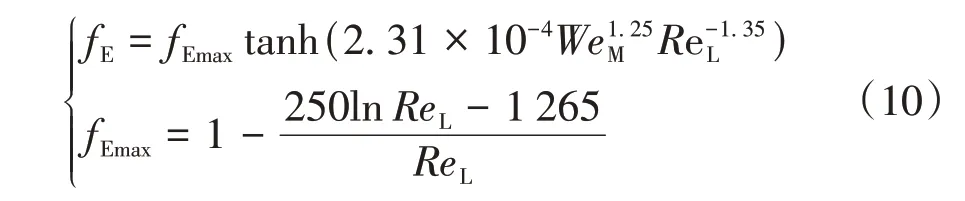
其中,WeM为修正韦伯数;ReL为修正雷诺数.
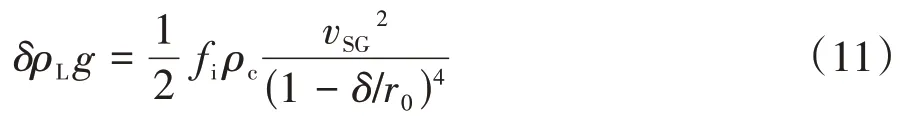
液膜刚反转时,气芯拖曳力等于液膜重力,为其中,fi为内摩擦因子;ρc为气芯密度,单位:kg/m3.
fi可采用FORE等[12]提出的模型进行计算,
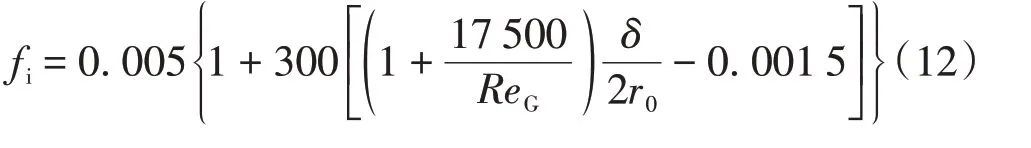
其中,ReG为无因次气相雷诺数.
由式(11)可得液膜反转时对应气流速度为
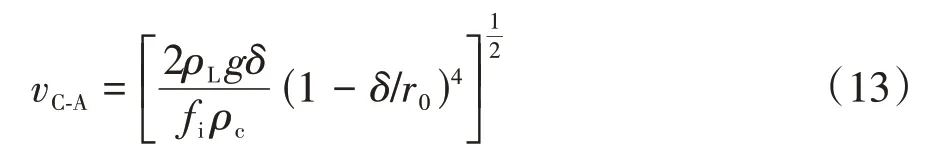
与此同时,基于液膜厚度和液滴夹带率即可求出环状流-搅动流转变点对应持液率为
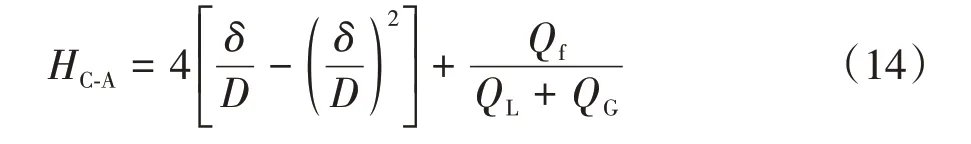
2.2.2 搅动-段塞流及段塞-泡状流转变点
搅动-段塞流和段塞-泡状流转变点可采用漂移模型进行计算,对于垂直管中气液两相流而言,漂移模型可表示为

其中,C0为速度分布系数;vd为气相漂移速度,单位:m/s.
气液混合速度则是气液表观流速之和,为

其中,vSL为液相表观流速,单位:m/s.
由式(15)和式(16)可得

对于漂移模型而言,最为关键的是确定速度分布系数和气相漂移速度,而两者都是与流型相关的参数.对于速度分布系数,在泡状流和段塞流时,C0通常取值为1.2.对于气相漂移速度,在段塞流时,气相上升速度采用BENDIKSEN[13]建立的泰勒气泡在静液中的上升速度关系式
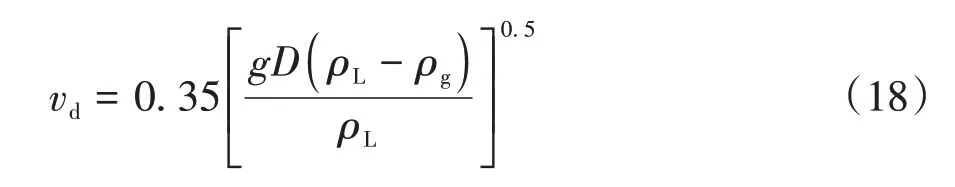
根据TENGESDAL 等[14]的研究成果,含气率大约在0.78 时段塞流向搅动流过渡.由式(17)和式(18)可知,段塞-搅动流型转变点的气流速及持液率分别为
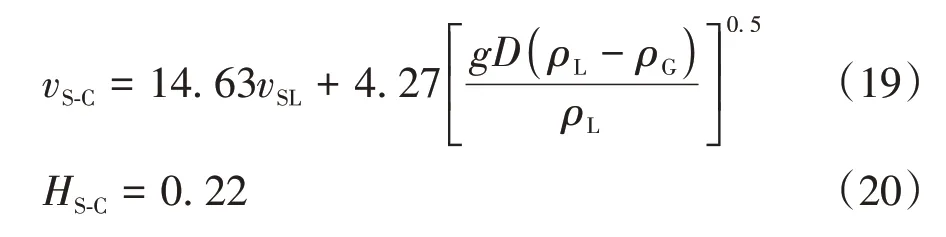
而在泡状流时,气泡在液相中的流动遵循HARMATHY[15]在静止液柱中的上升速度关系式
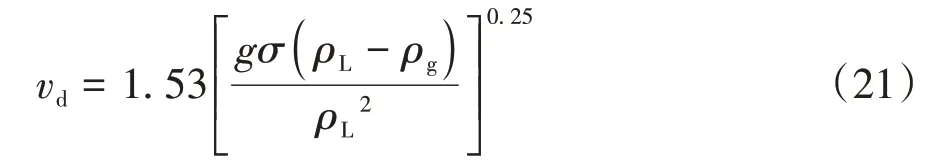
其中,σ为气液表面张力,单位:N/m.
根据Hasan&Kabir 模型[16]和Ansari模型[3],泡状流向段塞流过渡时含气率大约为0.25,由式(17)和式(21)可知泡状-段塞流型转变点的气流速及持液率分别为
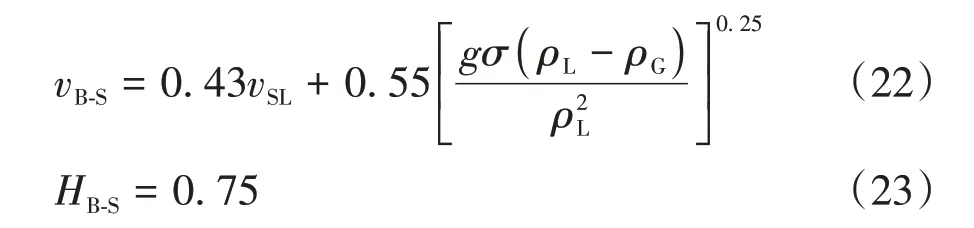
2.3 系数求解及极值处理
基于式(3)以及各流型转变点对应气流速及持液率值,首先采用牛顿迭代法迭代求解系数B.
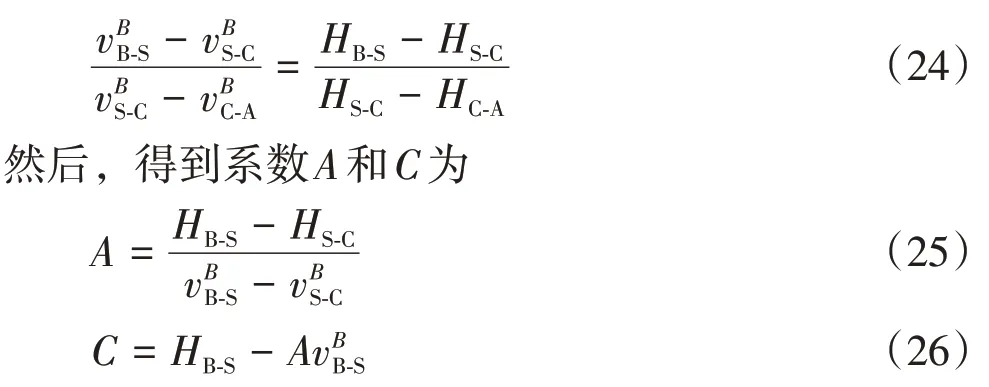
本研究模型基于半经验模型建立,在气流速过大或过小时会导致计算持液率失去物理意义,因此有必要对极值进行限制.当气流速足够大时可能会导致计算持液率低于无滑脱持液率,此时将持液率定为无滑脱持液率;而当气流速足够小时可能导致计算持液率大于1,此时假定持液率等于1.
2.4 压力转化
尽管所提出持液率模型能够表征持液率随气流速变化规律,但在处理高压气井流动时,本研究发现,搅动-段塞流转变点模型存在适应性问题:以环状-搅动和搅动-段塞流转变界限为例对比说明,设定管径为50 mm,液流速为0.01 m/s,气体相对密度为0.6,温度为300 K,压力为1 MPa.图4 为流型转变界限随着压力变化的曲线,当压力约为7 MPa 时,预测的段塞-搅动流转变界限超过搅动-环状流转变界限.图5为流型转变界限随着液流速变化的曲线,在液流速大于0.42 m/s 时,段塞-搅动流转变气流速大于搅动-环状流转变气流速.这些情况与实际流动规律相悖,究其原因,对于段塞-泡状流转变点而言,液相为连续相,气泡为非连续相,流动稳定,气液滑脱速度根据气液密度差(即浮力)所建立,具有物理意义,因此能够较好地处理压力变化对持液率的影响.对于环状-搅动流转变点而言,气相为连续相,液相为非连续相,持液率采用气液动量守恒计算得到,也具有明确的物理意义;而对于段塞-搅动流转变点而言,流动从液相为连续相向气相为连续相转变,泰勒气泡本身向上流动不稳定且上升速度采用经验关系式建立,而经验关系式基于低压实验所建立,因此模型难以处理压力变化对持液率的影响.
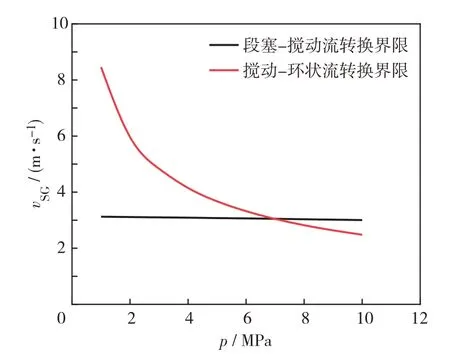
图4 预测流型转变点随压力变化曲线Fig.4 Curves of predicted flow pattern transition points of slug-churn(dark line)and churn-annular(red line)with pressure.
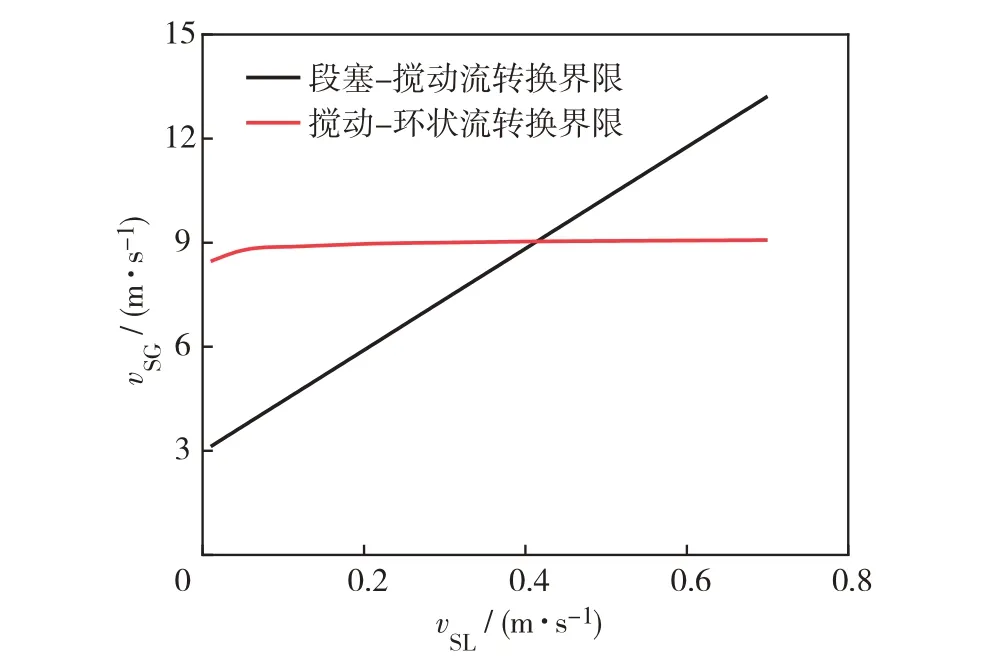
图5 预测流型转变点随液流速变化曲线Fig.5 Variation curves of predicted flow pattern points of slug-churn transition(dark line)and churn-annular transition(red line)with liquid superficial velocity.
综上所述,采用经验方法建立的段塞-搅动流转变界限尽管在低压实验中具有较高的预测精度,但是在高压时由于辅助方程适应性预测能力较差.为此,本研究所建持液率模型先基于流动条件建立常压下的3点曲线方程,随后采用HEWITT 等[17]的坐标准数,利用流动相似性,将高压系统气流速转化到低压系统[18]中,
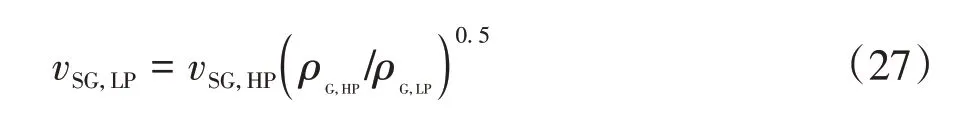
其中,vSG,LP为低压系统气相表观流速,单位:m/s;vSG,HP为高压系统气相表观流速,单位:m/s;ρG,LP为低压系统气体密度,单位:kg/m3;ρG,HP为高压系统气体密度,单位:kg/m3.
3 倾斜管持液率预测方法
上述持液率预测方法仅适用于垂直管段中.而对于水平井而言,角度变化使得流型界限以及持液率变化规律变得更加复杂,难以明确其流型转变点和预测其持液率.BEGGS等[9]根据实验测得的水平段持液率数据,建立了倾斜校正系数随角度的变化经验关系式,以表征管道倾角对持液率的影响;MUKHERJEE 等[7]持液率模型直接将角度考虑为正弦函数的多项式;陈家琅[19]则直接通过回归得到了持液率随角度变化的指数幂方程.综上可知,倾斜管持液率预测可根据相同条件下不同角度下倾斜管与垂直管持液率的对应管径关系,利用垂直管的持液率值进行预测.现有模型的回归均是基于较宽液量范围得到的,对于气井低产液量而言,可预测性较差.为此,基于Belfroid 角度修正关系式[20],本研究提出用于角度修正的持液率预测方法

其中,Hθ为倾斜管持液率;HV为垂直管持液率;D、E和F为模型系数.
采用吴朋勃[21]的实验数据拟合可得模型系数分别为:D=0.12、E=1.6、F=0.94.图6 为不同气流速下模型预测与计算持液率结果对比.由图6可见,该模型在不同条件下均能较好地表征持液率随角度变化趋势.
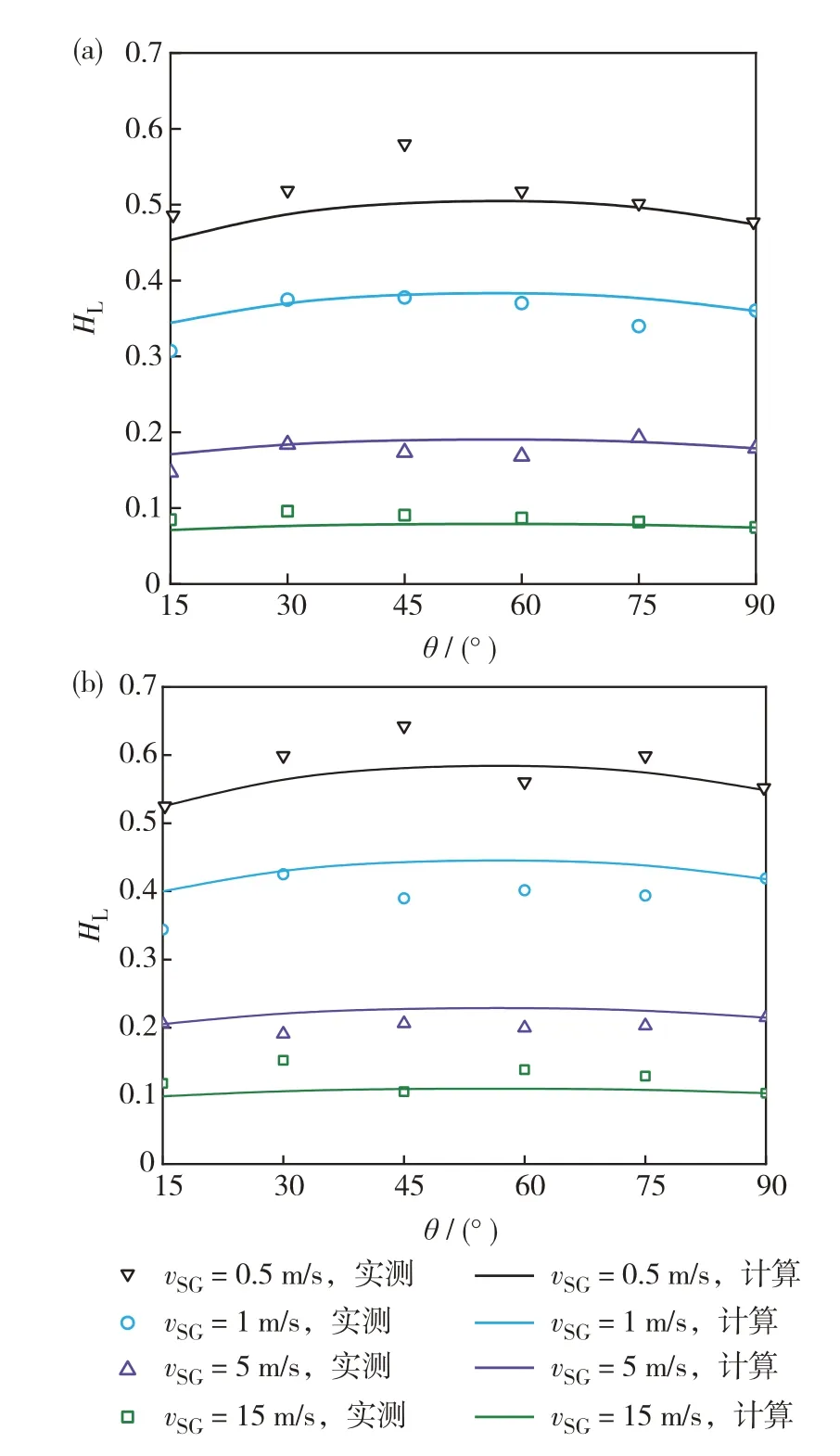
图6 不同气流流速下(a)vSL=0.01 m/s和(b)vSL=0.1 m/s时模型持液率对比Fig.6 Comparisons between calculated and measured liquid holdups of(a)vSL=0.01 m/s and(b)vSL=0.1 m/s at vSG of 0.5 m/s(black),1 m/s(blue),5 m/s(purple),and 15 m/s(green)with scatters for measured values and lines for calculated values.
4 模型对比与实例验证
采用文献[22-24]中压力数据及四川页岩气测井数据,对本研究构建模型的预测精度进行验证,并与Mukherjee &Brill(M-B)模型[7]、Gray 模型[8]、Hagedorn &Brown(H-B)模 型[25]、Ansari 模 型[3]和Zhang模型[26]进行对比.
4.1 文献数据
参考文献[22-24]中3个数据组,数据组生产参数范围如表1,分别提供了38井次、102井次(94井次数据可用)和50井次的实际垂直井测压数据.数据组分别覆盖了低、中、高产气量范围,产液和压力范围也均较为广泛,具有较强的代表性.模型误差采用文献[27]中定义的平均百分误差(E1)、绝对平均百分误差(E2)、百分标准差(E3)、平均误差(E4)、平均绝对误差(E5)和标准差(E6)对模型进行评价,并采用相对性能系数(relative performance factor,RPF)进行综合评价.RPF越接近0,表明模型性能越好.

表1 数据组参数范围Table 1 Data group parameter range
图7 为各模型的误差对比图.从图7 可见,本研究构建的新模型预测数据点更贴近45°线,绝大部分数据点均在±10%误差线以内,表明了新模型在不同压力条件下均具有良好的预测能力.从表2的评价结果来看,在6个评价指标中,新模型仅平均百分误差E1略高于Hagedorn&Brown 模型,其他指标均为最低,RPF也仅为0.01,在所有模型中最低,表明新模型具有良好的预测性能,能够满足不同生产条件下压力预测.
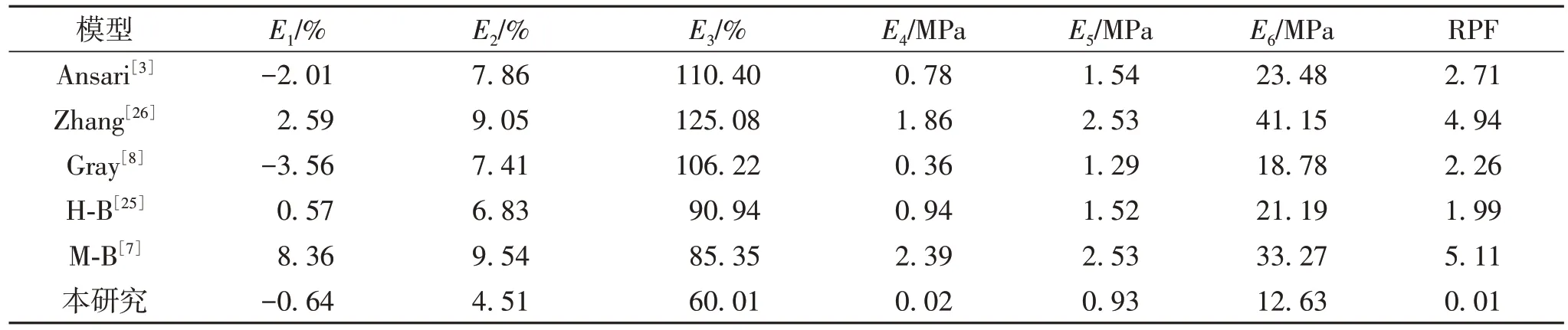
表2 各数据模型评价结果Table 2 Model evaluation results against literature data

图7 各模型误差对比Fig.7 Comparison of errors of Ansari model(black squares),TUFFP model(red circles),Gray model(blue triangles),H-B model(green triangles),M-B model(purple rhombuses),and the proposed model(yellow triangles).
4.2 四川页岩气测井数据
上述文献数据均为垂直井筒中测压.为评价模型在水平井中预测性能,本研究收集了四川页岩气14井次的测压数据(表3).通常而言,气井生产测井只会下入到一定井斜角,因此,数据并未能覆盖所有角度,最大井斜为52°,但考虑持液率随角度变化以及重力降随井斜增大而迅速降低的趋势,该数据组能够评价新模型在水平井中的性能.对比结果如表4所示,新模型RPF仅为0.02,说明新模型在水平井中具有良好的预测性能,验证了模型方法的正确性.
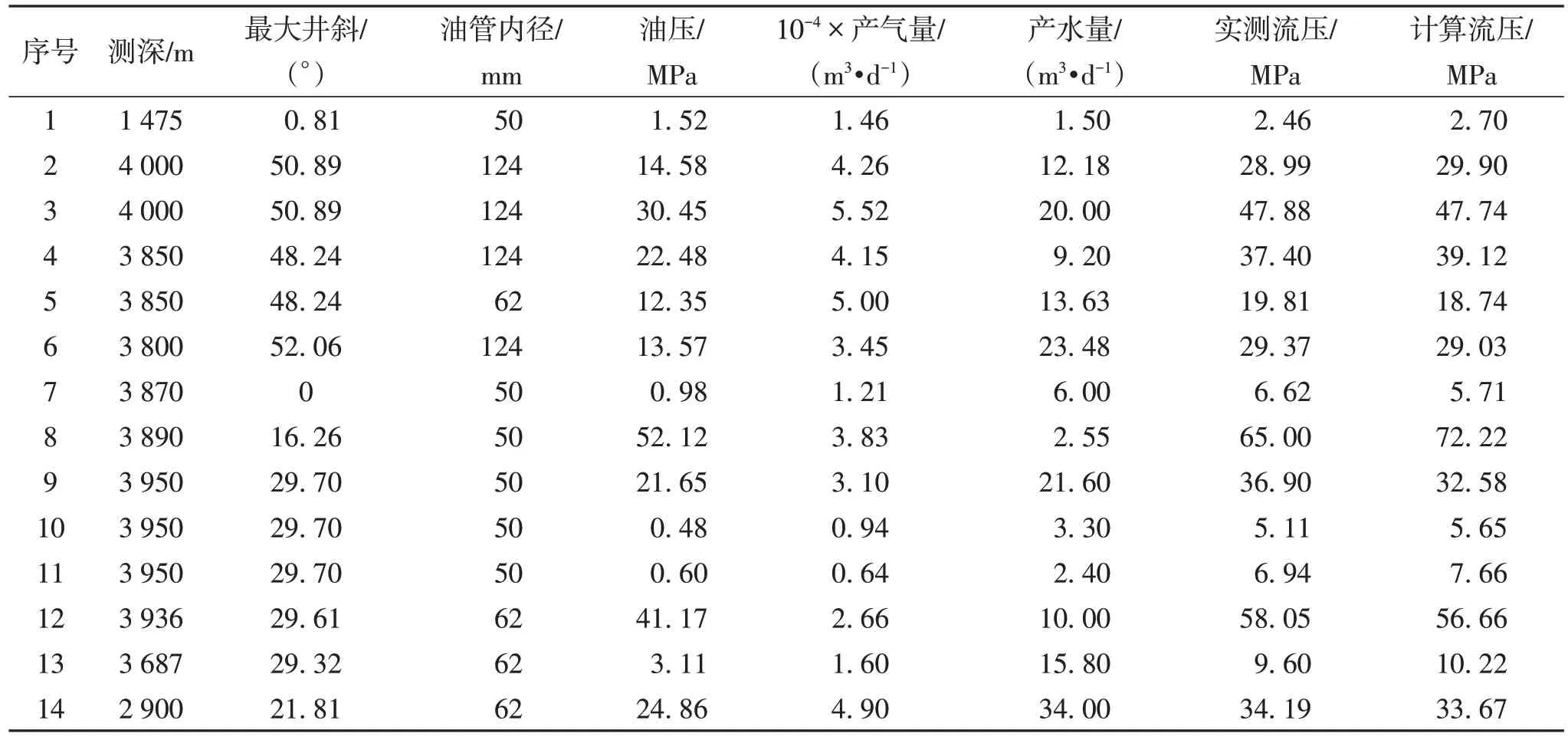
表3 新模型预测结果与气井测压数据的对比1)Table 3 Comparison of measured and predicted pressures
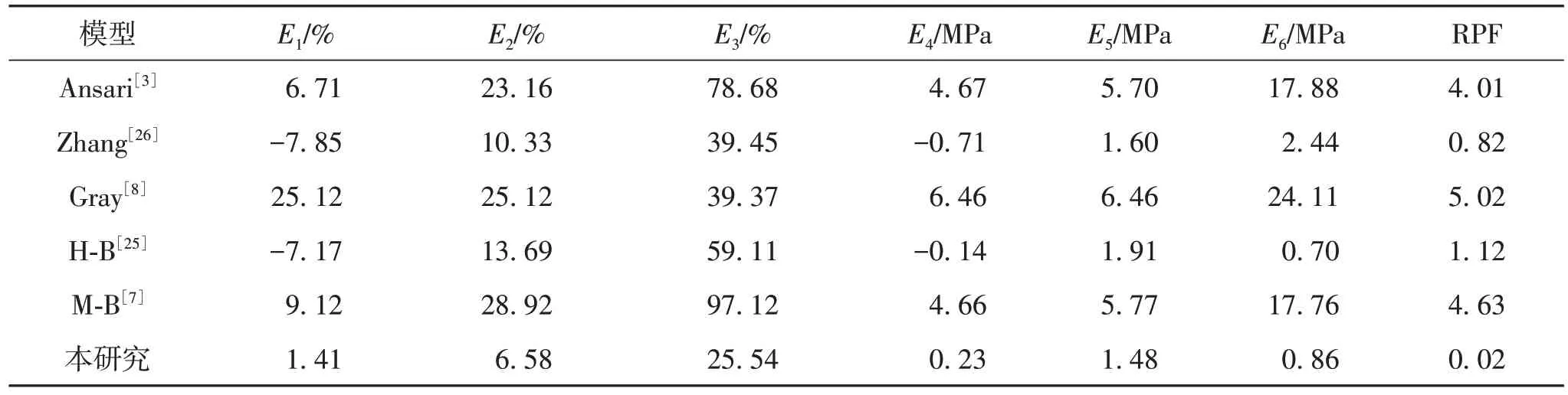
表4 测压数据模型评价结果Table 4 Model evaluation results against measured data
5 结论
1)非环状流时,井筒摩擦阻力占比很小,气井井筒流体压降研究的核心为持液率的准确预测.
2)基于环状-搅动、搅动-段塞和段塞-泡状3个流型转变点,提出垂直井筒持液率3点曲线半经验模型,模型能够捕捉持液率随气流速的变化趋势,不受实验参数范围影响,具有良好的推广运用前景.
3)井筒持液率随着管道倾角的增加先增加后降低,倾斜管持液率可基于垂直管持液率及其对应关系预测得到.
4)新模型与文献数据及四川页岩气测井数据的相对性能系数在所有对比模型中最小,表明模型能够满足工程计算精度要求.

