临床研究中交互作用、效应修饰的识别和评价

王瑞平 李斌

（上海市皮肤病医院临床研究与创新转化中心 上海 200443）

临床医学研究尤其是在病例对照研究和队列研究设计中，研究者在评估“暴露与结局”的关联强度时，往往须要控制其他因素的影响，进而得到“暴露与结局”的真实关联强度。影响临床研究“暴露与结局”评估的因素主要有两大类，一类是包括混杂偏倚在内的各种系统误差所导致的偏倚，研究者应对此进行识别和控制；而另一类是交互作用和效应修饰，是两个或多个因素相互依赖发生作用而产生的一种效应，对暴露因素作用于结局变量的效应起到“增强”“协同”“拮抗”等作用，研究者应对此进行识别和评估。本文将介绍交互作用和效应修饰的概念，交互作用的识别方法，以及评估交互作用和效应修饰的策略等内容，以期为研究者今后开展交互作用和效应修饰评价提供参考。

1 交互作用/效应修饰的概念

临床研究中，交互作用一般指两个或多个因素相互依赖发生作用而产生的一种效应。在生物学上是指两个或多个因素相互依赖发生作用而引起疾病或预防控制疾病；而在统计学上，交互作用说明两个因素在数量上的关联。交互作用的识别和分析有利于描述疾病的特征，探索疾病的病因，在公共卫生领域和临床上均具有重要意义。如果人群中的交互作用是由两个因素引起，称为效应修饰，主要变现为协同作用和拮抗作用。协同作用（synergism）是指两个因素的联合作用大于他们单独作用之和；而拮抗作用（antagonism）是指两个因素的联合作用小于他们单独作用之和。通常，可以通过分层分析对交互作用和效应修饰进行识别。

2 交互作用/效应修饰的识别

如本刊2022年第43卷第15期“临床研究中混杂偏倚的识别和控制策略”[1]一文中所述，在临床研究中，研究者须要识别并控制潜在的混杂偏倚；而对于交互作用，研究者则须要识别并对其进行描述和评价，而不是进行控制。同样，分层分析是识别交互作用的常用方法。为方便研究者理解，本文仍引用“一项口服避孕药（oral contraceptive, OC）和心肌梗死（myocardial infarction,MI）病例对照研究”[2]并对数据进行适当调整，以举例说明。

在该项研究中，考虑到年龄与OC有关，也与MI有关，即考虑年龄是潜在的混杂因素。因此，将年龄按照＜40岁和≥40岁分为两层，由此来判定年龄是否为OC与MI关联的潜在混杂因素。如图1所示，首先，根据提供的原始数据计算出OC与MI之间的关联强度，即比值比（odd ratio, OR）＝2.20，95%置信区间（confidence interval, CI）：1.26～3.84。随后，根据混杂因素判定的3个条件：①先判定年龄是否与OC有关，摘取两层对照组患者数据（图1中实线框数据），计算出年龄与OC之间的关联强度OR为3.91；②其次再判定年龄与MI是否有关，摘取两层未服用OC患者数据（图1中虚线框内数据），计算出年龄与MI之间的关联强度OR值为0.24；③最后，结合年龄不是OC与MI发病的中间环节。由此可以得出，年龄是潜在的混杂因素。

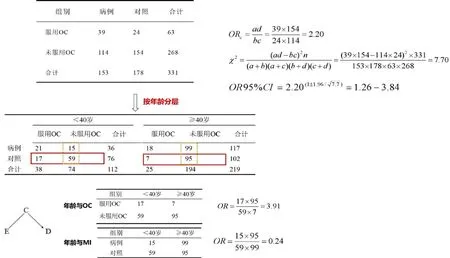
图1 应用分层分析识别交互作用

进一步分别计算两层中OC与MI之间的关联强度。在＜40岁年龄层，OC与MI之间的关联强度OR＝（ad）/（bc）＝（21×59）/（17×15）＝4.86；在≥40岁年龄层，OC与MI之间的关联强度OR＝（ad）/（bc）＝（18×95）/（99×7）＝2.47，两层之间的关联强度（4.86＞2.47）相差明显，说明年龄在OC与MI发病之间不均衡可比，年龄与OC之间可能产生了交互作用，共同导致MI的发生。

3 交互作用的评价

临床研究中，发现不同因素之间的交互作用后应进行描述和评价。而评价一项研究中是否存在交互作用，以及交互作用的大小均依赖于模型，这主要包括了相加模型和相乘模型。为方便理解，本文将以图示的方式进行说明。

如图2所示，假设A和B是某人群中与疾病D有关联的2个危险因素。A0B0表示A和B两个因素均不存在；A1B0表示A因素存在B因素不存在；A0B1表示B因素存在A因素不存在；A1B1表示A因素和B因素均存在。同理，R00表示某人群既不暴露于A因素也不暴露于B因素的发病概率；R10表示某人群暴露于A因素而不暴露于B因素的发病概率；R01表示某人群暴露于B因素而不暴露于A因素的发病概率；R11表示某人群同时暴露于A和B两个因素的发病概率。

图2 应用分层分析识别交互作用

相加模型是评价基于同时起作用的A、B两个因素的超额风险等于A因素的超额风险加上B因素的超额风 险。 当（R11－ R00） ＝（R10－ R00）+（R01－ R00）时，说明基于相加模型A、B两个因素无交互作用；当（R11－R00）≠（R10－R00）＋（R01－ R00），说明基于相加模型的交互作用存在。在“一项吸烟与肺癌的队列研究”中，研究对象同时暴露于吸烟和石棉后的肺癌发病率明显高于仅暴露于吸烟的研究对象，以及仅暴露于石棉的研究对象。研究结果如图3所示，现应用相加模型评估吸烟和石棉在肺癌发生过程中的交互作用。根据相加模型理论，首先计算同时暴露于石棉和吸烟的肺癌发病风险（R11－R00）＝1 500－60=1 440；随后，分别计算仅暴露于石棉的肺癌发病风险（R01－R00）=300－60=240，仅暴露于吸烟的肺癌发病风险（R10－R00）＝300－60＝240；由此可得（R11－R00）＞[（R10－R00）＋（R01－R00）]。因此，基于相加模型，吸烟和石棉对肺癌的发生有交互作用，根据大小可判定为协同作用。须说明的是，在进行交互作用评价时，除发病率外，相对危险度（relative risk, RR）和OR同样也适用。两者判定公式分别为（RR11＋ RR00）＝（RR10＋ RR01）和（OR11＋ OR00）＝（OR10＋ OR01）。

图3 基于相加模型描述和评价交互作用/效应修饰

与相加模型相似，相乘模型是评价同时起作用的A、B两个因素的相对风险等于A因素的相对风险乘以B因素的相对风险。即当（R11/R00）＝（R10/R00）×（R01/R00）时，说明A、B两个因素基于相乘模型无交互作用；当（R11/R00）≠（R10/R00）×（R01/R00），说明基于相乘模型的交互作用存在。仍以“一项吸烟与肺癌的队列研究”为例，研究结果如图4所示，现应用相乘模型评估吸烟和石棉在肺癌发生过程中的交互作用。根据相乘模型理论，首先计算同时暴露于石棉和吸烟的肺癌发病相对风险（R11/R00）＝1 500/60=25；随后，分别计算仅暴露于石棉的肺癌发病相对风险（R01/R00）＝300/60＝5，仅暴露于吸烟的肺癌发病风险R10/R00＝300/60＝5；由此可得（R11/R00）＝（R10/R00）×（R01/R00）。因此，基于相乘模型，吸烟和石棉对肺癌的发生无交互作用。同样地，在进行交互作用评价时，除发病率外，还可以运用RR或OR进行判定。两者判定公式分别为（RR11×RR00）＝（RR10×RR01）和（OR11×OR00）＝（OR10×OR01）。

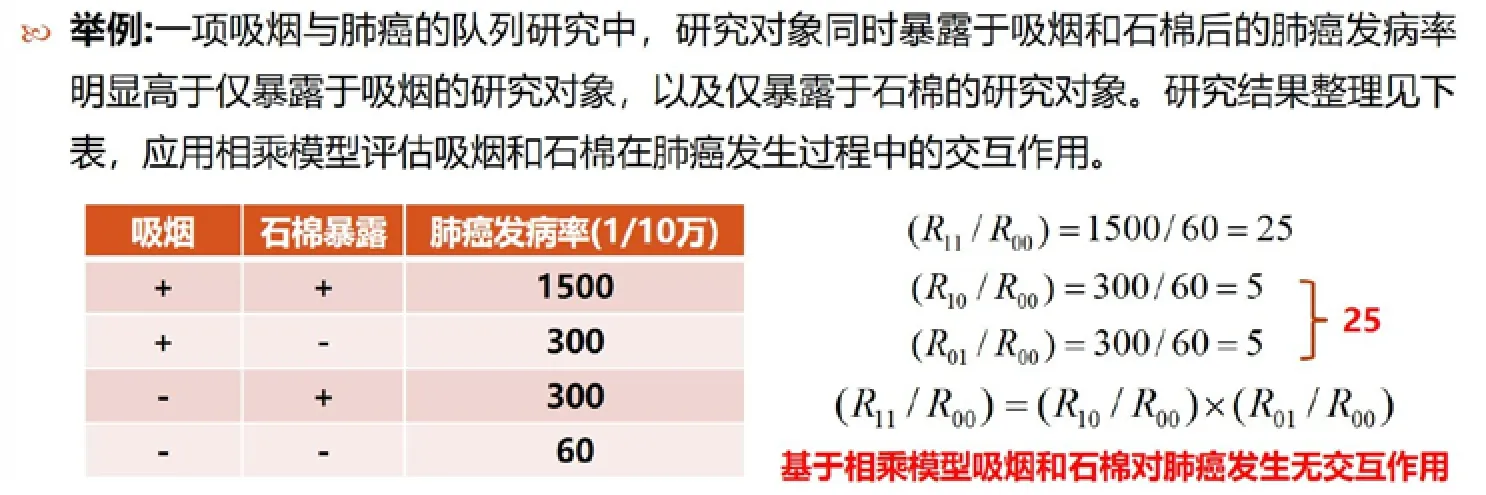
图4 基于相乘模型描述和评价交互作用/效应修饰

综上所述，相加模型是评价同时起作用的A、B两个因素的超额风险等于A因素的超额风险加上B因素的超额风险，而相乘模型是评价同时起作用的A、B两个因素的相对风险等于A因素的相对风险乘以B因素的相对风险。须注意的是，在临床研究中，相加模型适用面更广，而相乘模型多数用于基因相关的研究。另外，研究交互作用可以帮助人们了解这些因素的生物学特征，但是混杂因素并不是一个因素的固定不变的特征，其在一项研究中可能起到混杂的作用，却也可能在另一项研究中，起到的是交互作用。因此，临床研究中可能会出现以下4种情况：①有混杂，但无交互作用；②无混杂，仅为交互作用；③混杂和交互作用同时存在；④混杂和交互作用均不存在。研究者在评价时应根据具体情况进行分析。

至于在前文所提到的“一项OC与MI病例对照研究”中，运用分层分析初步识别年龄和OC对MI存在潜在的交互作用后，接下来即可开展交互作用的描述和评价。如图5所示，首先根据分层后的数据进行叉生分析，计算OR11、OR10、OR01、OR00；然后分别用相加模型和相乘模型进行评价：基于相加模型，得到（R11－R00）≠（R10－R00）＋（R01－R00），即年龄和OC对MI基于相加模型存在交互作用；基于相乘模型，同样得到（R11/R00）≠（R10/R00）×（R01/R00），即年龄和OC对MI基于相乘模型也存在交互作用。

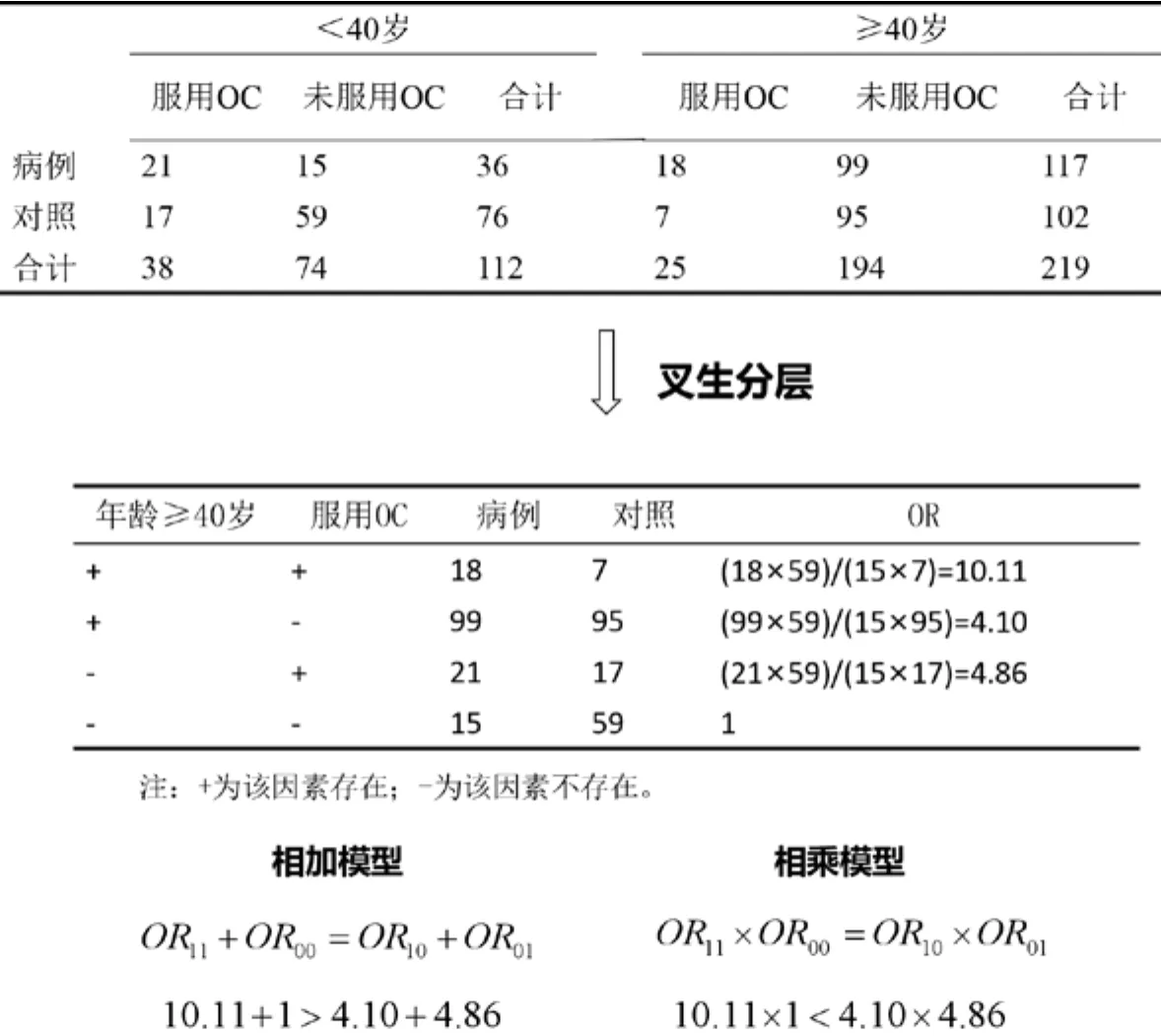
图5 年龄和OC对MI影响的交互作用评价