KYN断路器温升算法探索

黄慕斌 辜建雄 林凯

（广东正超电气有限公司，广东汕头 515000）

0 引言

现代电力设备小型化、高功率密度的发展趋势，使得热管理在产品设计、型式试验、在线监测方面的重要性更加突出。在电力开关柜中，温升是影响导线载流能力的重要指标。从技术上讲，确保各部件在其合理的温度范围内工作，避免超温、超负荷运行是非常必要的。

1 本文任务

本文通过建立温升模型，计算和验证KYN断路器热属性常数，并拟合出电流值跟对应的最大温升的关系。

2 温升模型算法推导

KYN断路器热源都来自于断路器室和电缆室。电缆室中热量绝大部分都是由通电的导体产生的；断路器室热源主要有两部分，一部分是通电的导体产生的，另一部分是断路器连接触头的接触电阻产生的[1]。

断路器梅花触头的接触电阻由收缩电阻和膜电阻组成。收缩电阻指的是电流经过断路器触头和导线连接处时，由于导电面积减小而增加的电阻；膜电阻是由于接触表面受到污染产生的薄膜而增加的电阻。接线端子的发热与接触电阻、导体电阻、电磁线圈的涡流发热有关[2]。散热主要通过断路器表面和电缆产生热传导的方式传出。

取KYN断路器梅花触头的发热散热做分析，梅花触头发热量Q约等效于导体电阻R1和断路器的接触电阻R2的发热量之和。假设通过电流为I，时间为t，热量Q可以表示为：

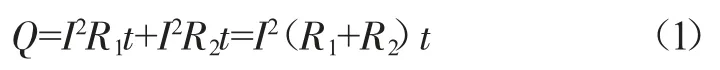
根据能量守恒定律Q=Q吸+Q散，在dt时间内，断路器触头的温升为dτ，得：

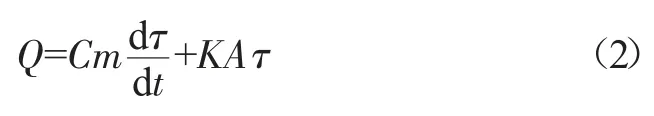
将式（1）代入式（2）得：

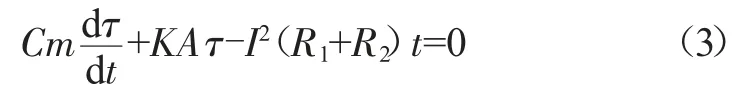
式中：C为断路器的比热容；m为断路器的质量；K为断路器设备的散热系数；A为导体的表面积；I为断路器的电流。

解式（3）得：

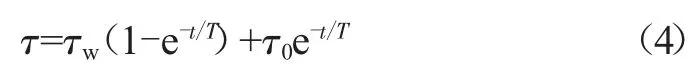
其中，τw=I2（R1+R2）/KA，T=Cm/KA。

由式（4）可知，梅花触头的最终温升跟断路器触头的电阻以及断路器设备固有的结构有关。当梅花触头连接固定时，断路器的稳定温升只跟通过导体的电流正相关。

把方程（4）改写为：

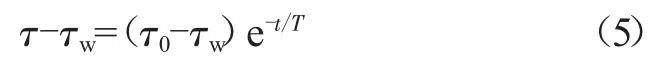
两边取自然对数得到：

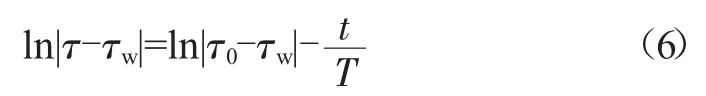
设y=ln|τ-τw|，x=t，a=ln|τw-τ0|，b=-1/T，则方程（4）的非线性回归问题可以化作线性回归：

根据最小二乘法原理可以求得a、b：

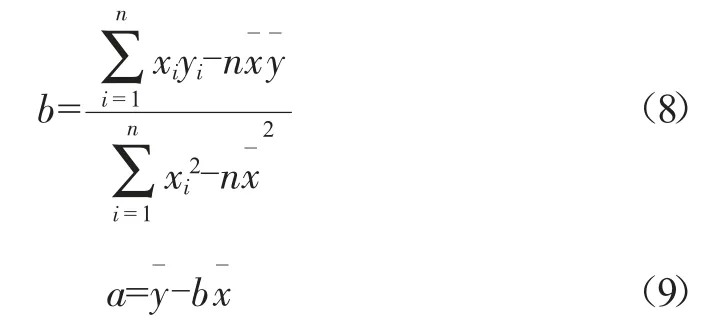
求得最大温升和热时间常数的关系式：

由于y=ln|τ-τw|含待求量τw，无法直接通过线性回归方式求得参数a、b，可以结合数值分析方法来求得。

某次测得的温度的时间为（t1，τ1），（t2，τ2），（t3，τ3），…，（tn，τn），假设τw的值为τ1w，按xi=ti、yi=ln|τ1w-ti|输入数据，通过最小二乘法求出参数a1，b1代入式（10）可以求出τw的计算值τ11w：

当δ1w=0时，τ1w即稳定温升τw的推算值，这个过程相当于求超越方程：f（τw）=ea+τ0-τw=0（τw≥τ0）或者f（τw）=τ0-ea-τw=0（τw＜τ0）的根。

采用逐步迭代法来求得该方程的τw的值。函数f（x）具备连续单调性质，f（x）=0存在解，使得f（a）f（b）＜0，且x∈（a，b），f（x）=0。只要找到（a，b）区间并逐步缩小该区间使得最终求得的f（x）小于一定的精度要求即可求得τw和T的值。

具体求解过程如图1所示。

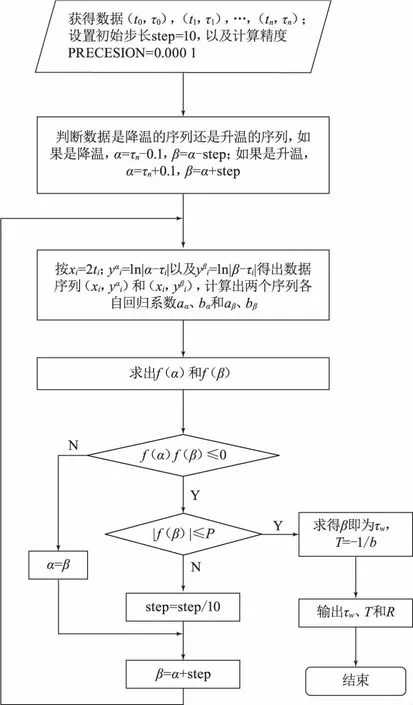
图1 求解过程

由以上算法可以计算出KYN柜电流对应的稳定温升值（I1，τw1），（I2，τw2），（I3，τw3），…，（In，τwn）。假设τw（I）=aI2+bI+c，下面通过最小二乘法推算出KYN柜电流和稳定温升的拟合曲线。

设：

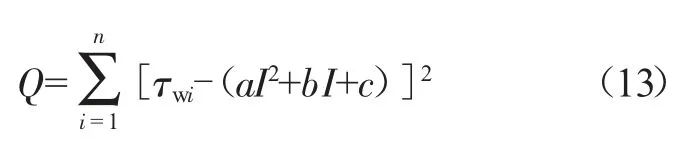
Q分别对a、b、c求偏导数得：

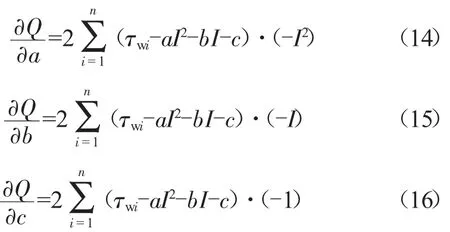
令三个偏导数的值都为0可得最优解，即：

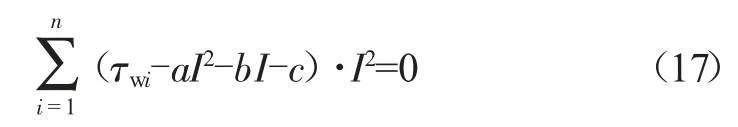
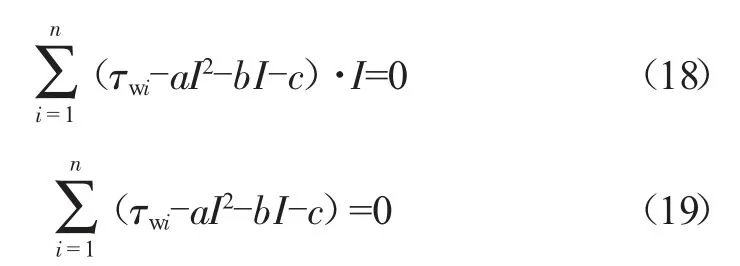
联立（17）（18）（19）三个方程可以求得系数a、b、c的值，这样就求出了KYN柜稳态温升跟电流的函数关系。

3 温升算法实践

3.1 拟合KYN柜体的热属性参数

采用连续60天温升房实验数据进行拟合，用拟合数据跟采集数据进行比较，计算出各个温度点的热属性常数。

图2、图3、图4是KYN柜三种电流的实际温升和拟合温升的曲线图，由图可看出拟合数据曲线和源数据曲线都很接近。从图3可以看出，电流不够大的时候，温升基本可以忽略。

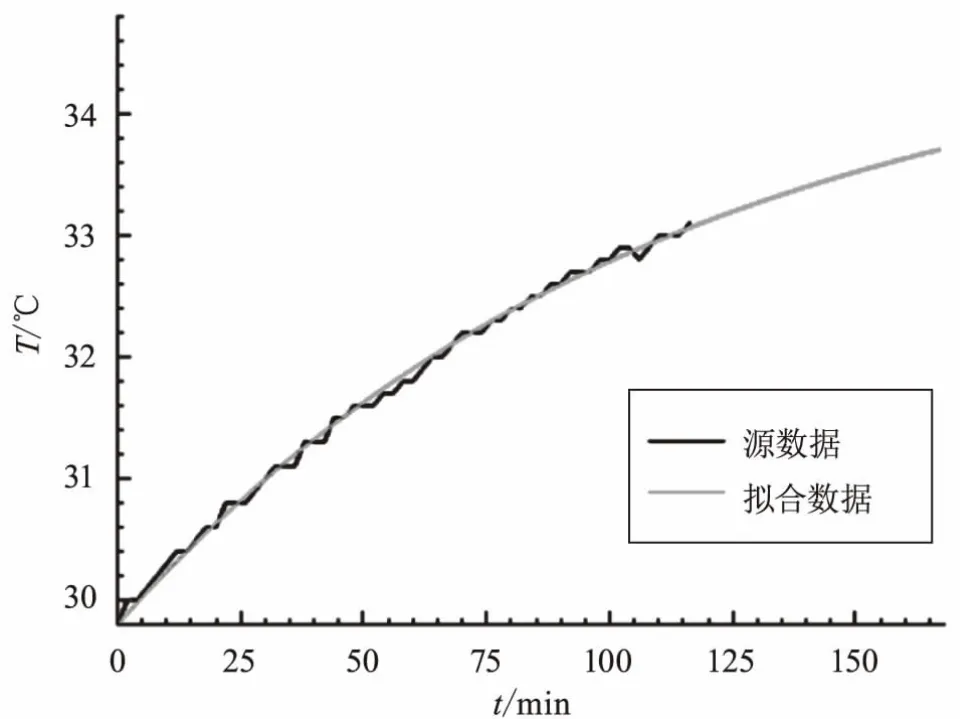
图2 电流1 200 A的曲线图

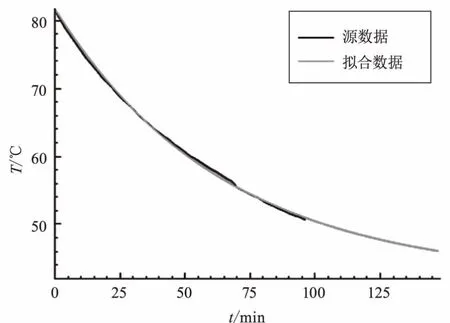
图3 电流700 A的曲线图

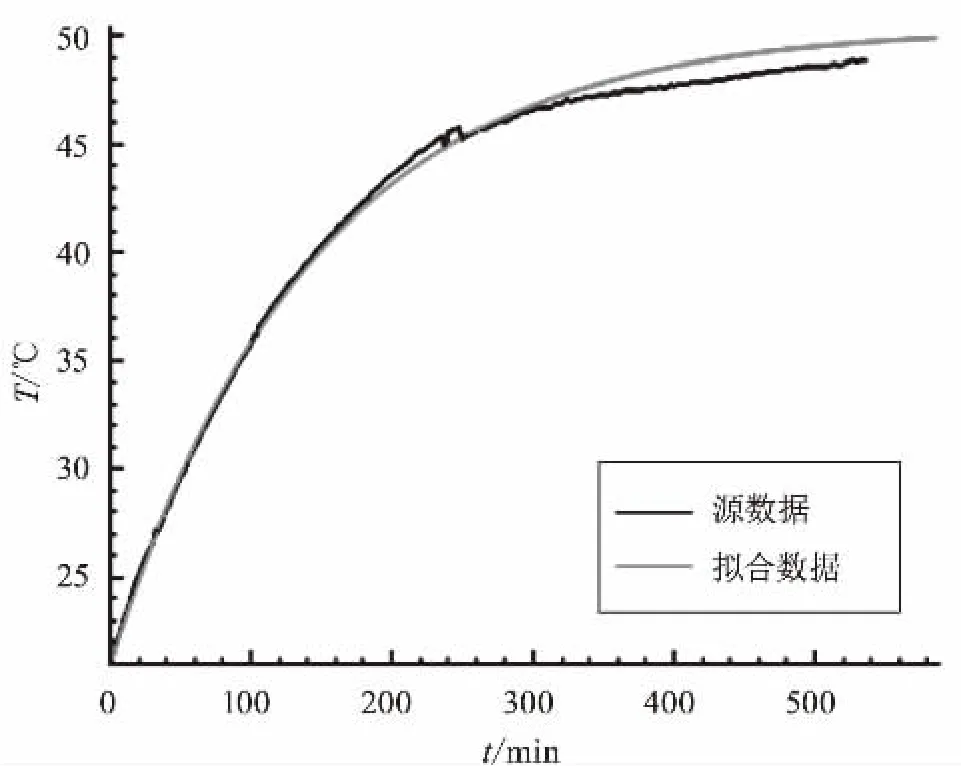
图4 电流2 000 A的曲线图

表1中理论稳定温升始终比实际温升大1～2 ℃，是因为实际稳定温升是一个经验值，规定只要在1 h内温度上升不超过0.4 ℃，读取的值即为实际温升。理论温升是指柜体内稳定电流持续运行无穷久时所能达到的温升值，是温升无限接近但无法到达的温度值[3]。

受实验时使用传感器精度和量程的限制，表2所采用的数据电流在采集点60以后发生下降，导致拟合出来的部分理论温升值偏低1～2 ℃。

由表1和表2可以看出，测量的数据跟模型拟合得非常好。但如果电流发生抖动，温升曲线容易变形，无法拟合或者拟合出温升特性常数存在偏差。如果发热电阻偏小通过的电流不大，通常需要等到温升值达到稳态时才可能准确地拟合出热属性常数。

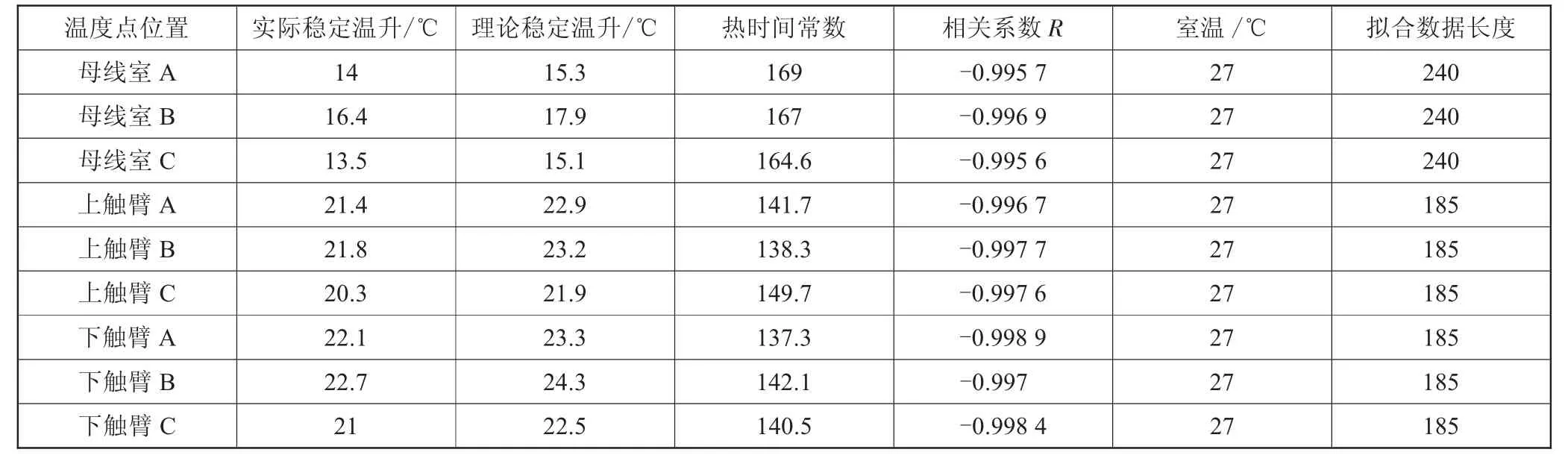
表1 KYN柜2 000 A电流拟合的热时间常数

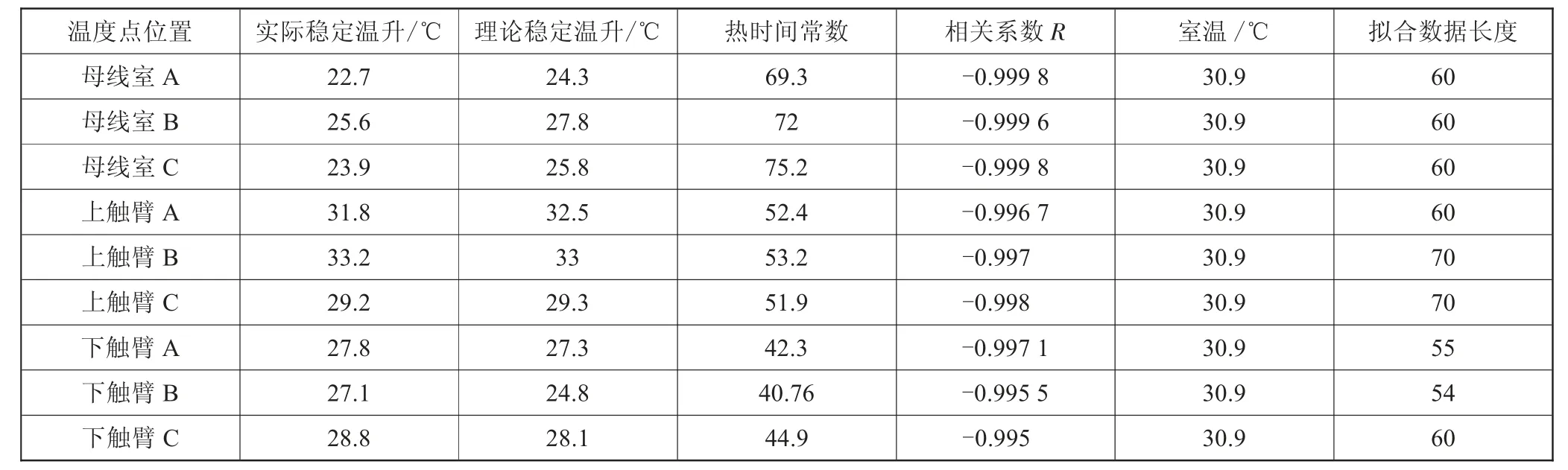
表2 KYN柜4 000 A电流拟合的热时间常数

总之，如果柜体内发热量足够大，可以形成温度场，电流也足够稳定，通过以上算法就可以准确地拟合出温升特性常数。发热量太小无法形成温度场，或者电流抖动太大导致温度场特征不明显，模型拟合不可能会成功。发热量越大，柜体内部形成的温度场特征越明显，拟合出柜体热属性常数所需要采集的数据就越少。

3.2 拟合设备电流跟最大温升的关系

在额定电流内选取几个电流点，每个电流固定不变运行一段时间，读取这段时间内的温度变化值，计算出其最大温升值和热时间常数；最大温升值再跟对应的电流序列拟合出经验公式。

计算出来的各个电流对应的最大温升值如表3所示。

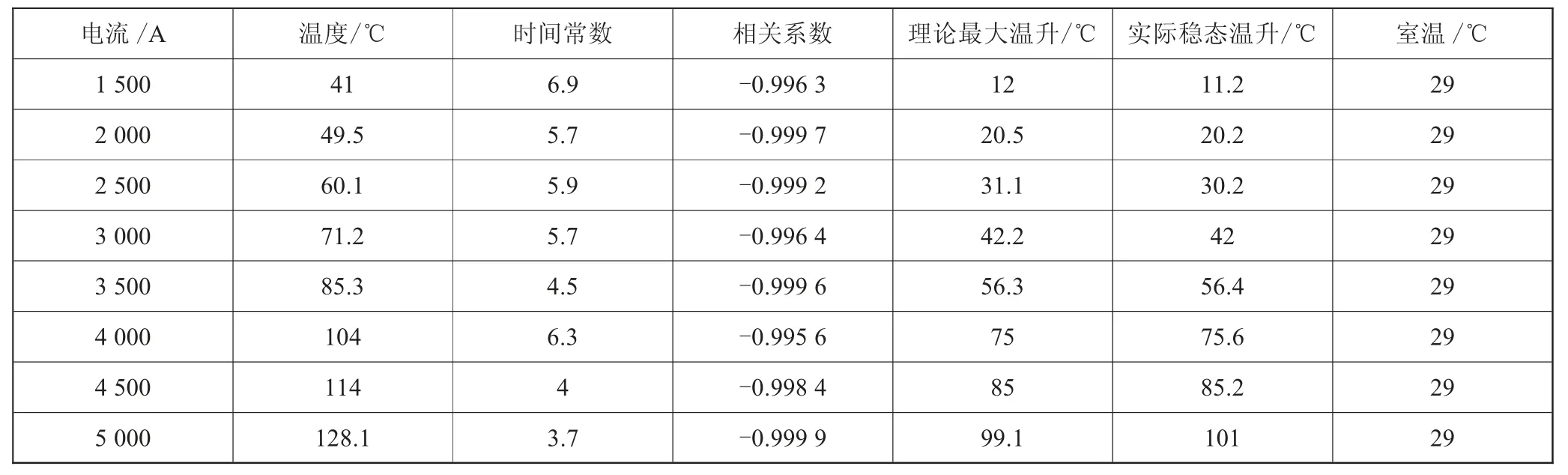
表3 温升—电流关系表

拟合电流跟最大理论温升可得经验公式：

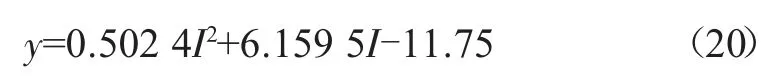
R2=0.996，I=10 A。

根据经验公式（20）可以计算出柜体在额定电流内任意某个电流的最大温升值。由图5和图6可知，实际温升和由公式（20）计算得出的温升误差在±1 ℃左右，经验公式基本符合要求。

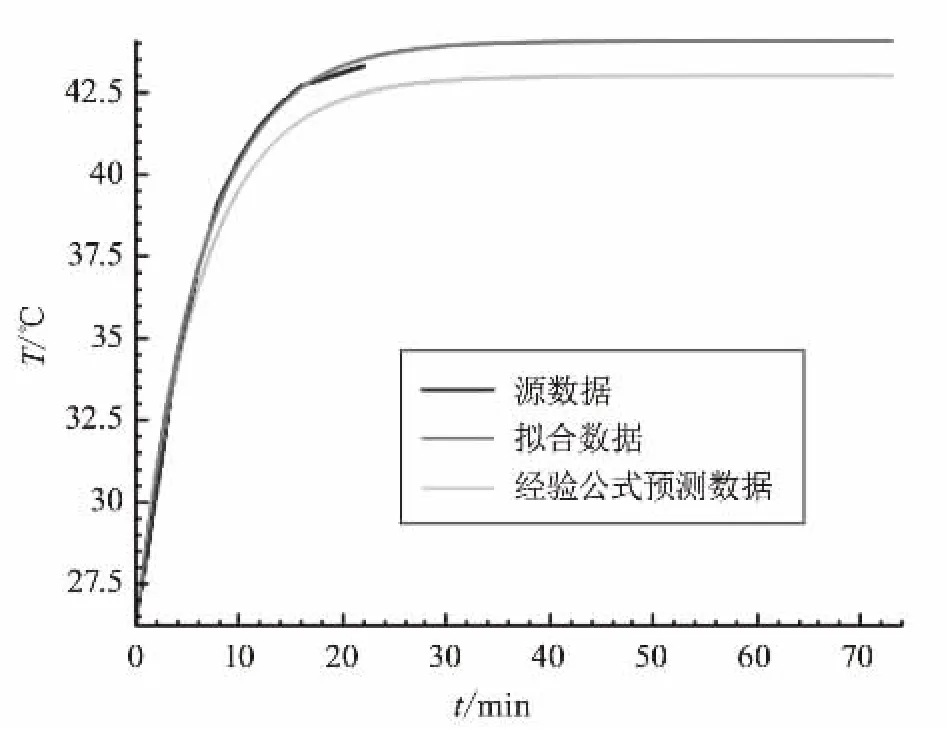
图5 电流为1 750 A时的温升数据

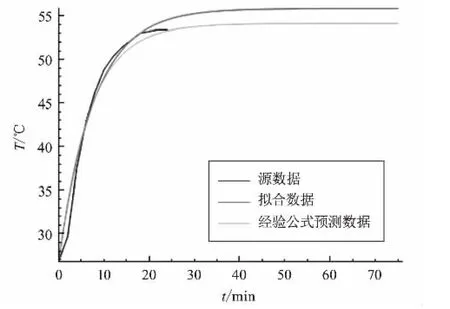
图6 电流为2 250 A时的温升数据

4 结语

理论推导和实践验证是新技术产品设计、生产应用的基础。本文展示通过理论推导、计算机仿真和大量实验，对KYN断路器温升预测技术进行探索，得到的温升模型能满足电力系统对温升误差的要求，为该技术在电力系统的应用提供了参考。