基于大型UUV的MPC解耦路径跟踪控制

詹康怡 马斌

（中国舰船研究设计中心，湖北武汉 430064）

0 引言

针对大型UUV的大惯性特性带来的控制响应较慢、控制效果滞后的现象，运动控制算法的选择须充分考虑对航行器趋势的预判与反馈修正，同时必须考虑到艉方向舵和螺旋桨的能力有限，不能频繁改变作用量。本文针对上述要求设计了控制算法和策略。

本文研究的对象是大型欠驱动对象，模型复杂。考虑到其大惯性的特点，当有较为精确的大型UUV模型时，MPC可以提高控制器对大型UUV未来一段时间内运动趋势的预测能力。为利用MPC预测控制的优点，并避免MPC在求解大自由度非线性系统时容易发散以及计算量大，不能满足实时计算的问题，针对大多数航行条件下UUV的水平面和深度面之间的弱耦合关系，将问题解耦为水平面控制与垂直面控制。对于水平面控制，进一步简化为运动学控制和动力学控制。采用基于视线角的虚拟导引法作为运动学控制器，首先在Serret-Frenet坐标系中进行视线角导航，并根据此导航角度设计控制率，最终控制率作为参考值输入动力学控制器；动力学控制器运用MPC算法，采用二次规划方法求得最优解。最后，在Simulink模型中使用S函数将这两部分结合起来，形成完整的控制器，并设计了仿真试验，仿真结果证明了该算法的有效性。

1 控制对象模型

考虑到水下无人航行器在大多数工况条件下，水平面与垂直面的运动耦合性不强，为突出体现算法，简化模型便于研究，本文仅对所控制对象模型的水平面模型进行研究。在仅考虑水平面的运动时可忽略垂荡、纵倾、横摇的相关运动学及动力学特性[1]，但为展示整体模型，在本节中仍写出完整模型，而在算法设计章节中分别展示解耦后的模型。完整运动学模型如下[2]：

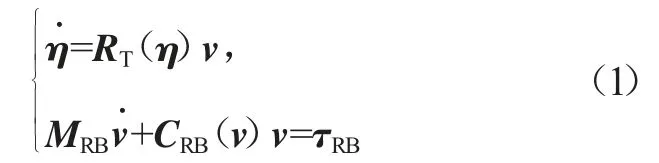
式中：η为UUV所有状态量的值所组成的向量；RT（η）为动系到定系的转换矩阵；v为状态量的变化速度；MRB（v）∈R6×6为惯性矩阵；CRB（v）∈R6×6为船体科里奥利向心力矩阵；τRB为UUV所受外力及外力矩所组成的向量。

η和v表达式如下：

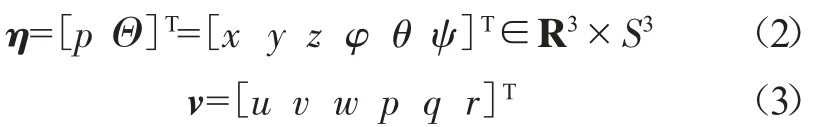
式中：x，y，z，φ，θ，ψ为状态量；u，v，w，p，q，r为状态量的变化量。

RT（η）的表达式如下：

式中：τH表示流体水动力（流体惯性力、流体黏性力）；τP表示静力（重力、浮力）；wH表示海洋环境力；τT表示推进器力；τR表示舵力；X∑，Y∑，Z∑为外力；K∑，M∑，N∑为外力的力矩。

MRB的表达式如下：

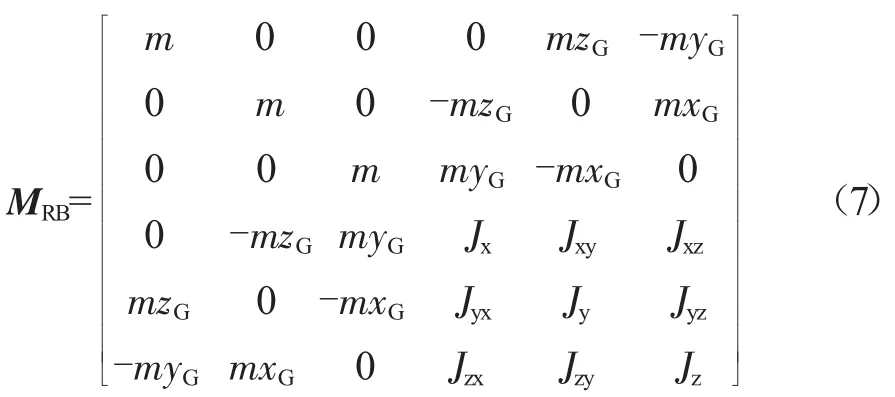
式中：m为UUV的质量；xG，yG，zG为真实位置坐标的向量表达式；J（·）为转动惯量。

CRB（v）的表达式如下：

根据所建立的六自由度模型，配合大型UUV水动力系数，得到后续仿真研究所使用的大型UUV数字模型。

2 控制器设计

考虑到在大多数工况下，水下航行器水平面与深度面的控制耦合性不强，针对水平面和深度面可单独设计控制器，下面仅以水平面为例对本文所设计的方法进行说明。

2.1 控制器架构

本文采用基于LOS的虚拟向导法与模型预测控制相结合，进行水平面控制[3-4]。控制器架构如图1所示。

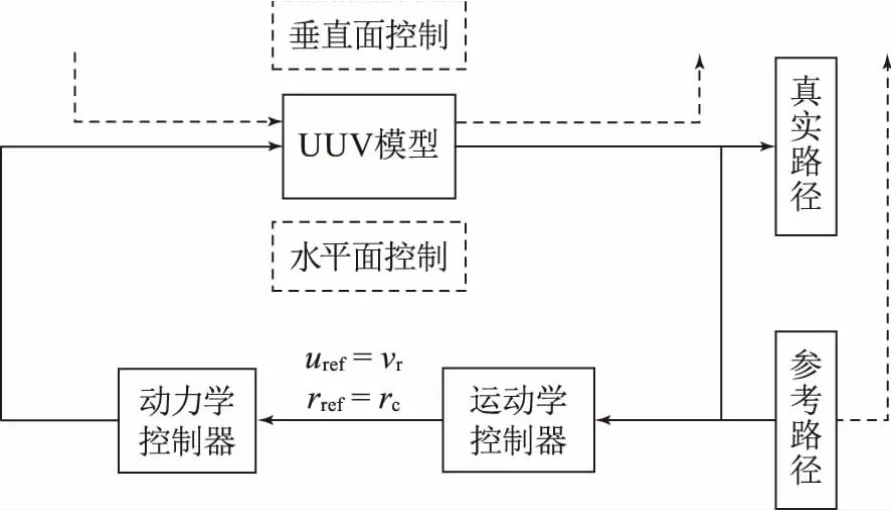
图1 控制器整体框架

2.2 运动学控制器设计

该部分对解耦后的水平面运动学模型进行控制，在无海流影响下，可得所研究的模型的水平面运动学模型，具体方程如下：

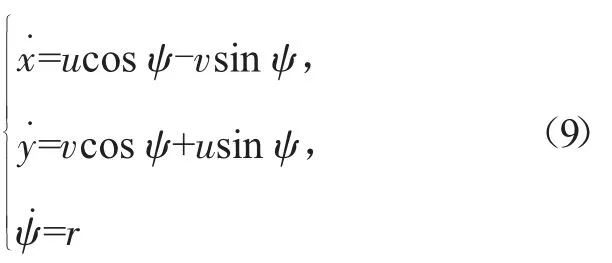
路径跟随部分的算法设计分为以下三个步骤：运动学方程转换、视线角导航、控制率设计。控制率的设计除了x轴方向的参考速度及艏向角的角速度，还增加了一个参考路径切向速度vr=s˙。相当于在参考路径上加入了一个虚拟向导，艇的控制中多了一个自由度的控制量。以下是具体的算法设计步骤。

2.2.1 运动学方程转换

Serret-Frenet坐标系是以参考轨迹上的点为原点，以该点引出轨迹的切向方向为x轴的坐标系，该坐标系的应用可简化侧漂角以及视线角的表达。该坐标系中运动学方程的建立，需要将惯性坐标系中的运动学方程进行转换，即左乘旋转矩阵，该旋转矩阵为惯性坐标系到Serret-Frenet坐标系的矩阵，图2为模型在Serret-Frenet坐标系中的示意图。

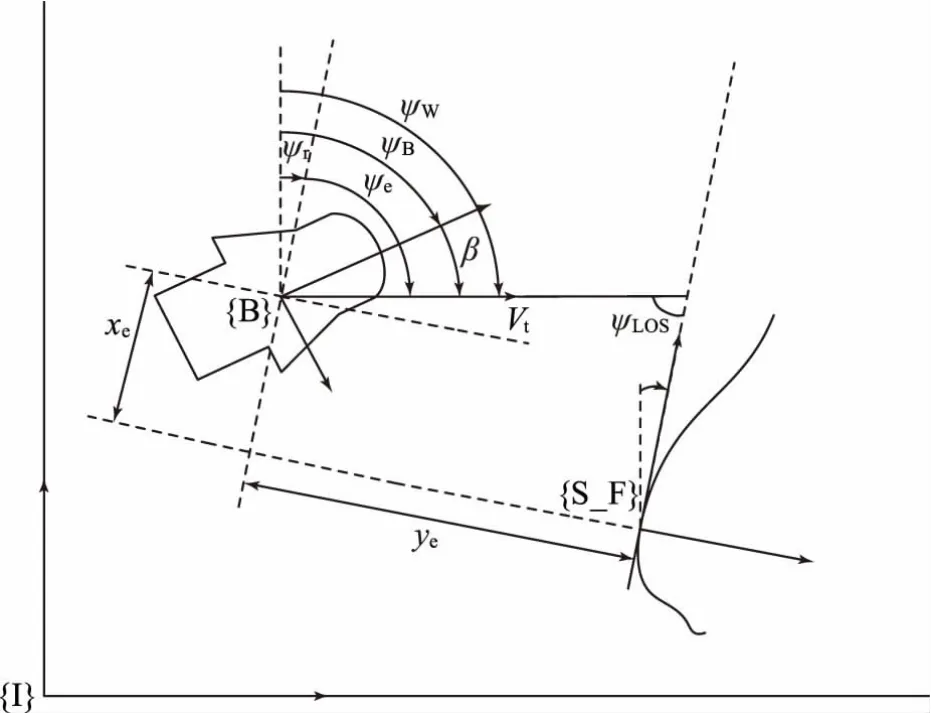
图2 模型在Serret-Frenet坐标系中的示意图

得到模型在Serret-Frenet坐标系中的误差模型表达式如下：

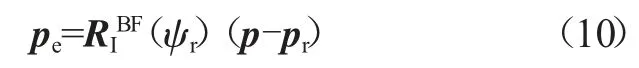
式中：RIBF为简化模型的转化矩阵；pr为参考值组成的向量。

式（10）可具体写成：

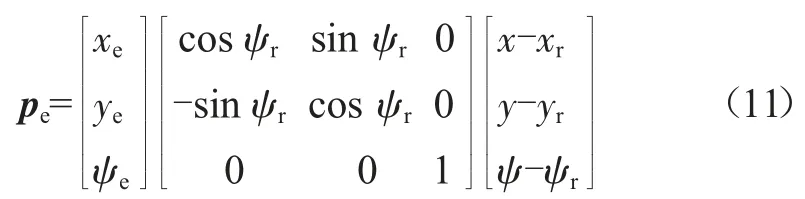
式中：pe为误差值组成的向量；xe，ye，ψe为误差值；xr，yr，ψr为参考值。

误差模型的一阶导数可写成如下公式：

式中：ωr为参考角速度；ωw为实际艏向角速度；vr为UUV横向速度参考值；vt为合成速度

2.2.2 视线角导航

这部分主要用于计算在Serret-Frenet坐标系中视线角的表达方法，图3为Serret-Frenet坐标系中视线角的表达。

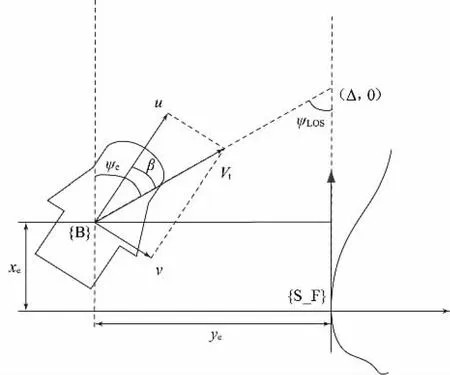
图3 Serret-Frenet坐标系中视线角的表达

2.2.3 控制率设计

给定参考路径s以及前向运动速度ud，跟踪误差pe=

式中：k1为正系数。

再选定另外一个Lyapunov函数：

对该函数进行微分：

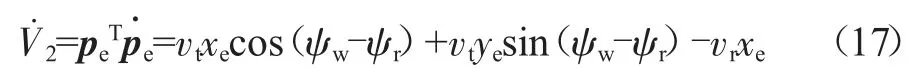
式中：ψw为合成速度vt与固定坐标系x轴的夹角；vr为UUV横向速度参考值。

同理，若要令V˙2≤0，即令V2为单调非增函数，可得速度控制率：

式中：k2为正系数。

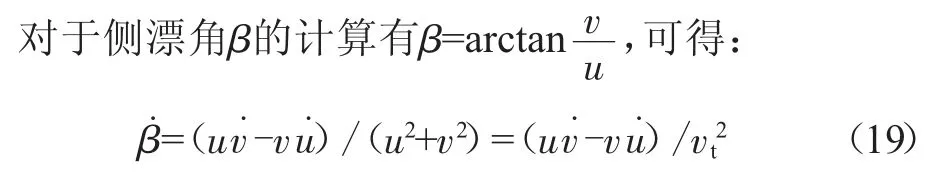
综上，运动学控制率为：

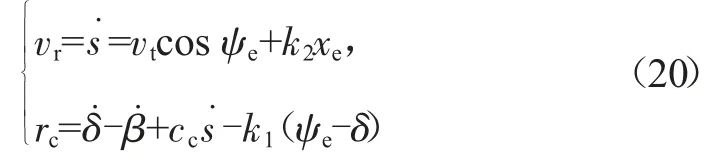
式中：vr为速度控制率，可将其视为路径上“虚拟向导点”的速度，会根据无人航行器与参考路径的位置关系即xe的值调整其自身数值大小，以引导无人航行器加速或减速运动。

2.3 动力学控制器设计

航向控制部分运用模型预测算法。对于该部分的控制器设计，需假设在此之前的轨迹跟随控制器可以实现一个“完美”的跟踪控制，令uref=vr，rref=rc，即将vr、rc作为参考值输入航向控制器。

该部分对解耦后的水平面动力学模型进行控制，将水平面动力学方程解耦出来，X2=[u，v，r]T为被控量，U2=[n，dr]T为控制量，有如下形式的动力学关系：

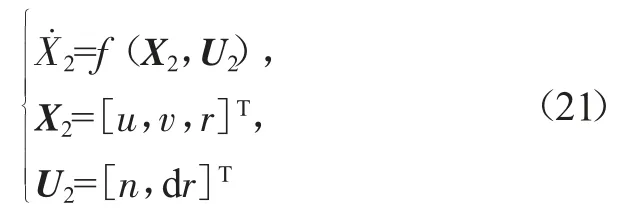
本文运用S-function将控制器与模型建立关系，可随时间变化不断将更新的控制量的值送入被控对象模型，同时再把模型的值输出到控制器，达到迭代更新的效果。

具体的动力学MPC控制器设计如下[4]：

首先对动力学关系式进行泰勒级数展开，忽略高阶项只保留一阶项，即对非线性模型线性化：

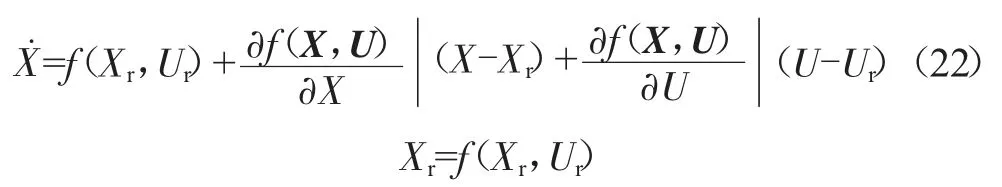
式中：f（Xr，Ur）为参考点处的值，Xr为状态量参考值，Ur为控制量参考值；X为状态量实际值；U为控制量实际值。

将上述两式相减得线性化的误差模型：

根据线性化的误差模型公式，运用前向欧拉法进行离散化处理：

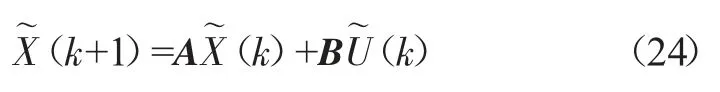
式中：A、B为雅克比矩阵。

为便于转化为标准二次型需要对式（24）进行适应化修改，如下：

经过推导，可得预测的输出如下：

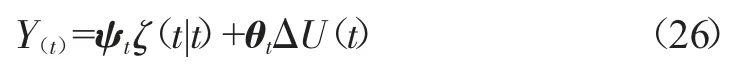
式中：Y（t）为预测输出值；ψt、θt为系数及参数组成的矩阵。

接下来进行目标函数的设计，为便于对每个采样周期里的增量进行控制，在传统二次规划函数中添加约束ρε2，可将目标函数写成如下形式：

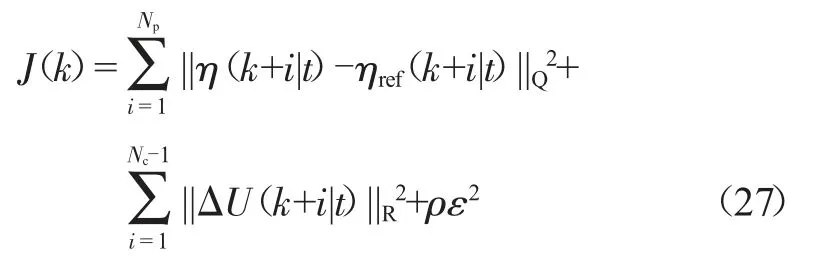
式中：Np为预测步长；Nc为控制步长；ΔU为控制量的变化值。

转换为标准二次型形式如下：

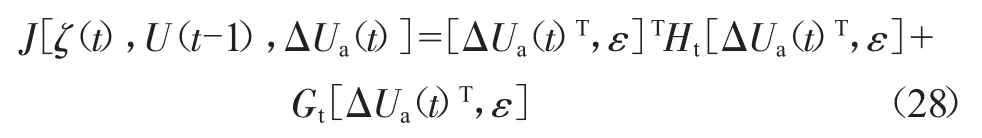
接下来进行约束条件设置，需要考虑的是控制量的表达式与控制增量的表达式，实际情况可以写成如下形式：

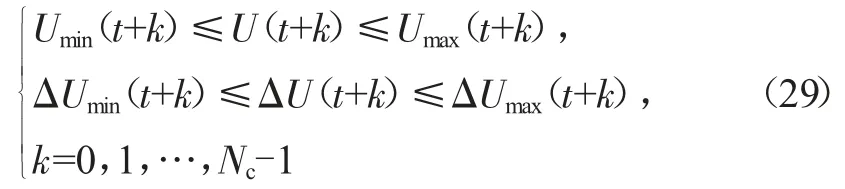
由于目标函数中没有关于控制量本身的计算，只有关于控制量增量的计算，因此需要将控制量约束转变成增量的约束，即需要对式（29）进行转换，因为存在如下关系：

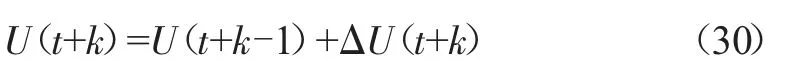
可令：

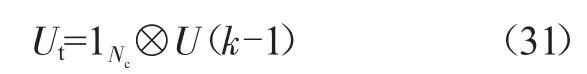
式中：1Nc为行数是Nc的列向量；⊗为克罗内克积（Kronecker product）。

综合上述分析，可将式（29）转换为如下形式：

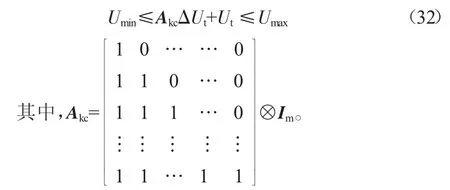
本文中设计的约束条件为：

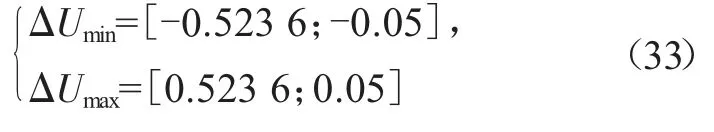
3 仿真验证

本节针对设计的控制器及特定的大型航行器被控对象，分别设计了正弦曲线及直线为参考路径进行仿真，以验证本文算法的有效性。

3.1 正弦曲线

参考轨迹如下，式中β为侧漂角，可利用上文中的侧漂角计算模块来计算。

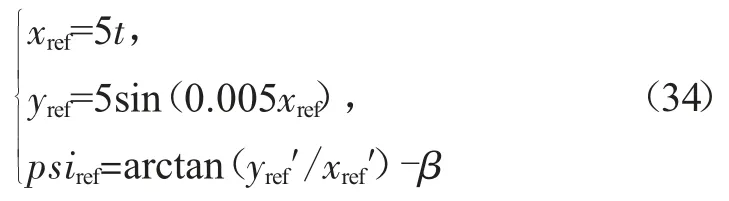
图4、图5为具体的正弦路径跟踪仿真图，由图可知，本文所设计的算法与MPC全控算法都能跟上参考轨迹，但可以观察到，MPC全控算法的误差较大，特别是在路径转弯处偏离最大，而本文所设计算法误差更小，且相对于MPC全控算法能较快收敛至参考轨迹；所设计控制器的两个控制量的变化基本也同状态量趋势一致，艉方向舵稳定后呈周期变化，转速稳定后为定值，而艏向角也能迅速反应并呈周期变化。

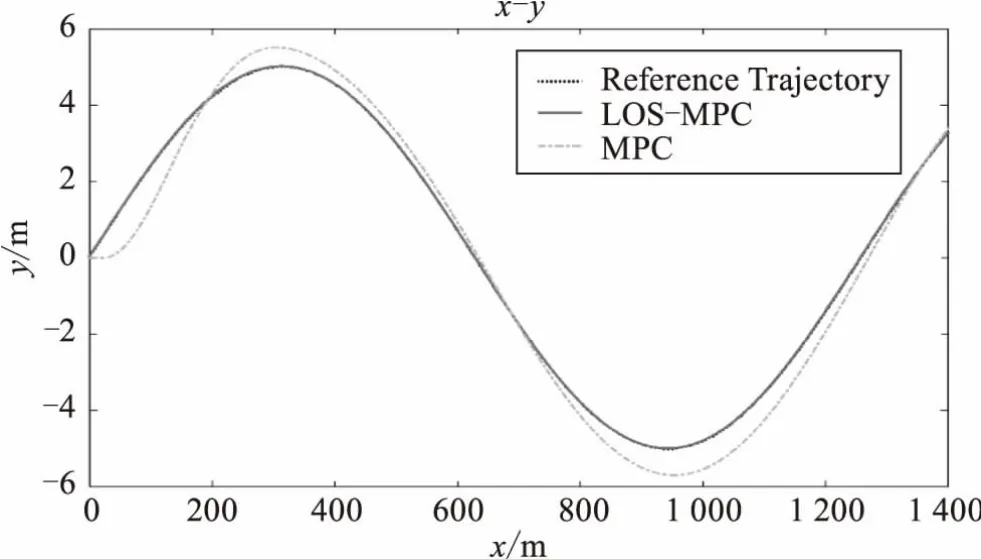
图4 正弦曲线跟踪效果图

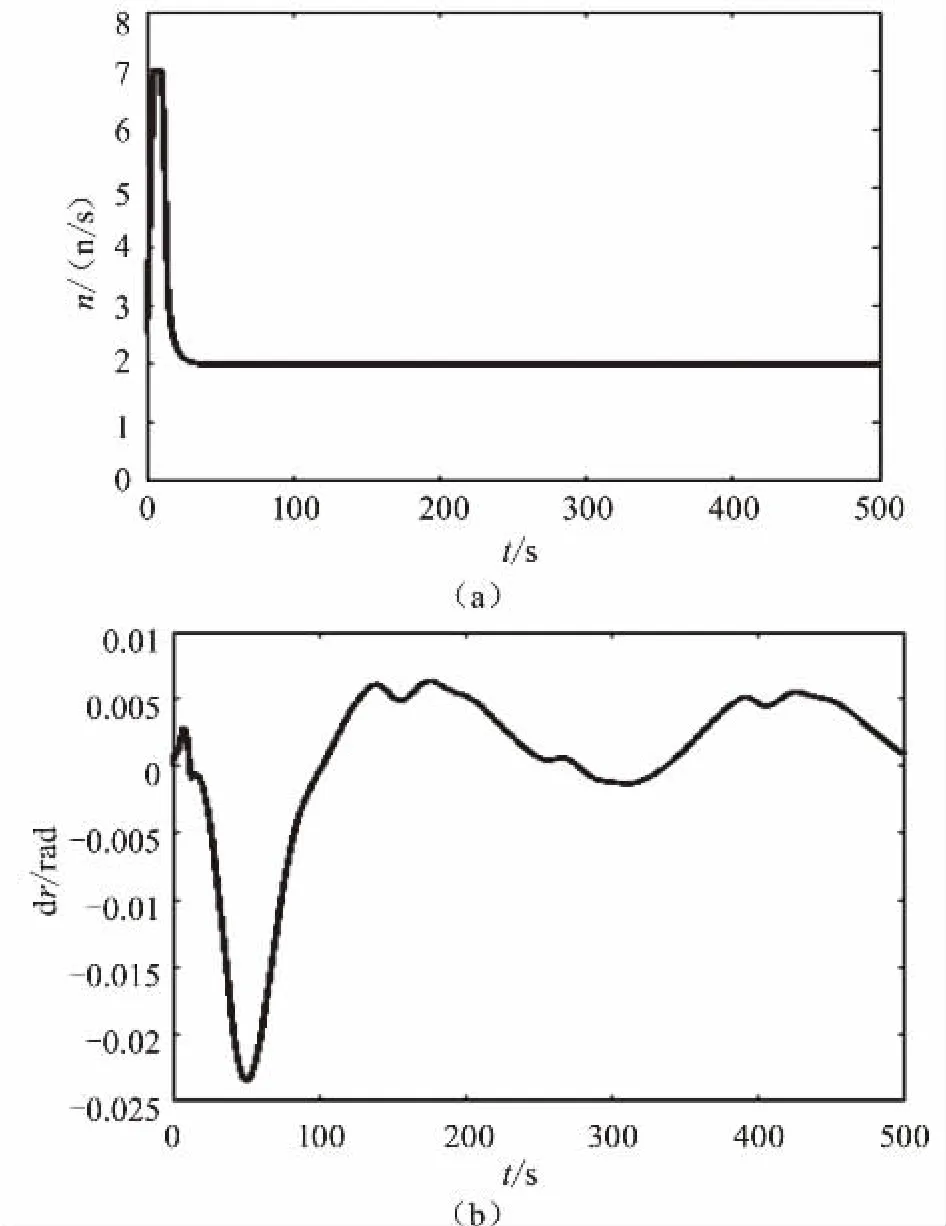
图5 本文算法控制量变化曲线

3.2 直线

参考轨迹设定如下，设定一起点不为零的斜线。

图6、图7为具体的直线轨迹跟踪仿真图，由图可知，本文所设计的算法与MPC全控算法都能跟上参考轨迹，但可以观察到，本文所设计算法收敛速度较快，与参考轨迹的误差较小，而MPC全控算法收敛速度相比较来说更慢，且在初始运动时与参考轨迹偏差较大；所设计控制器的两个控制量的变化基本也同状态量趋势一致，都在稳定后收敛于定值，与参考轨迹相符。

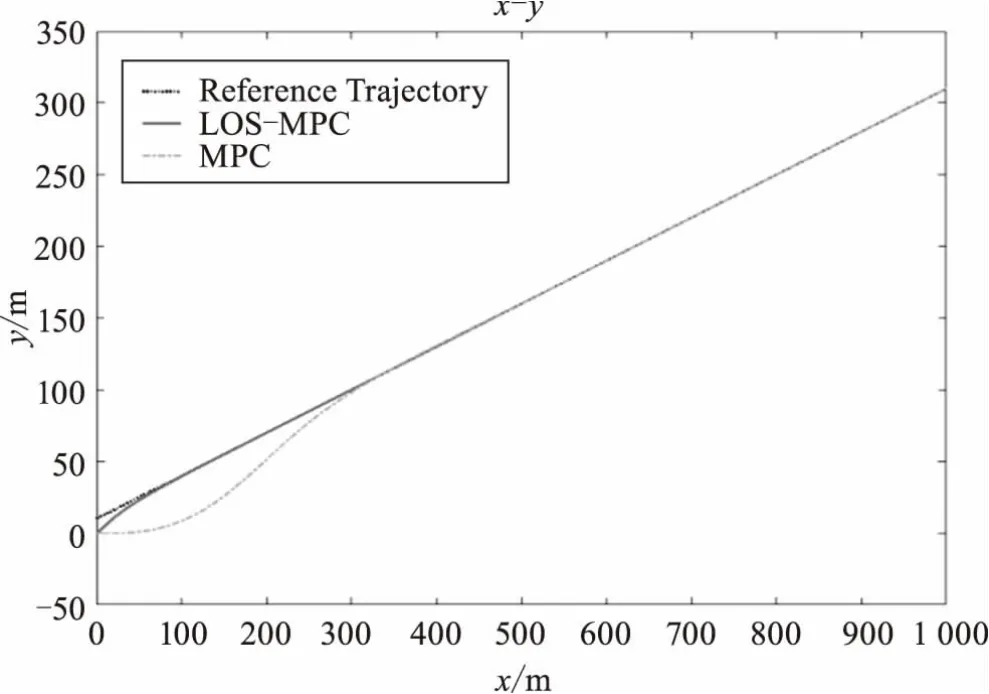
图6 直线跟踪效果图

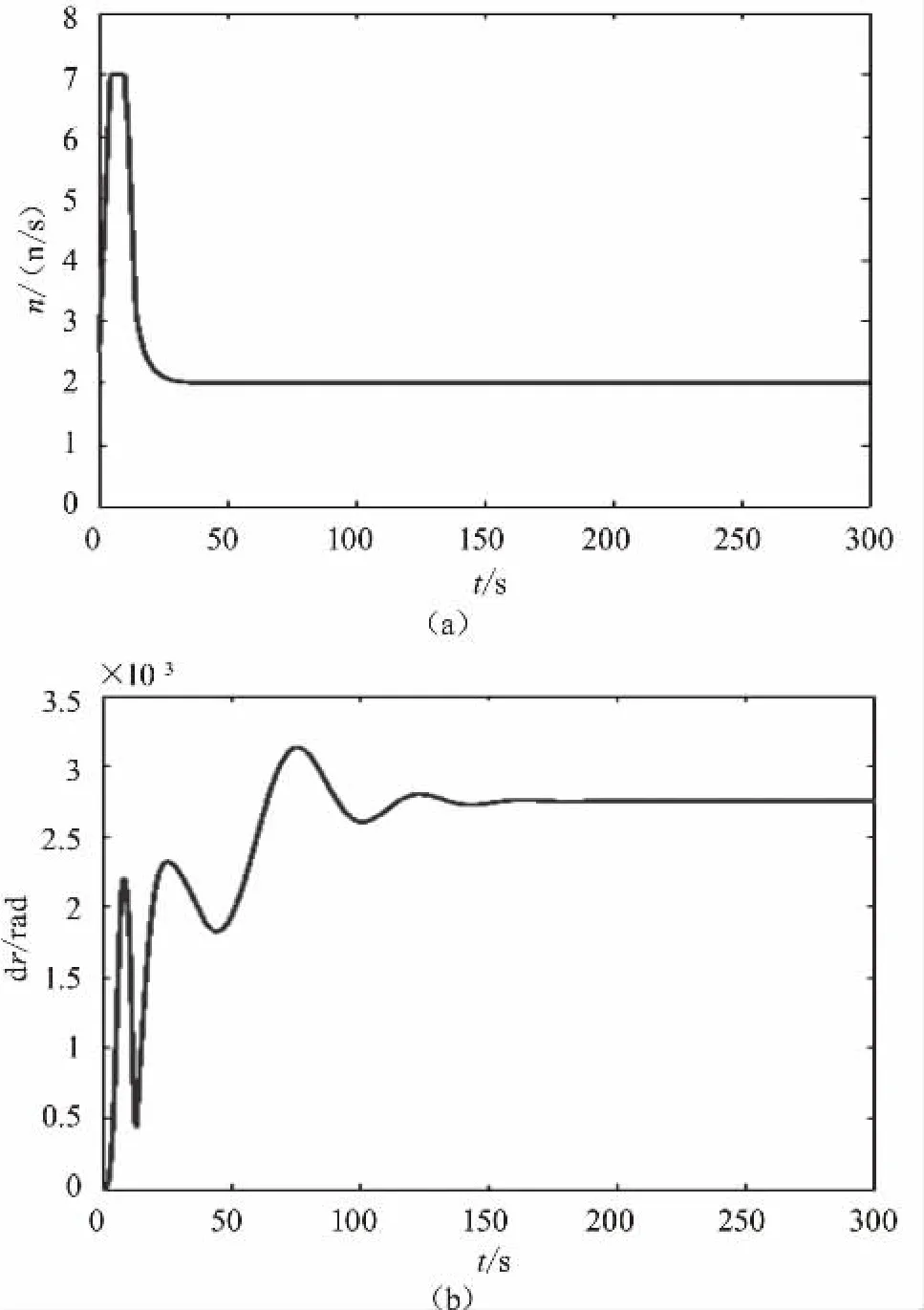
图7 本文算法控制量变化曲线

下面对比了本文算法与MPC全控算法每轮计算的时间，设计仿真实验分别统计了两种算法的计算时间，图8为具体仿真图。

由图8可以发现，本文所设计的算法每轮计算时间平均在0.005 s左右，而MPC每轮计算时间平均在0.015 s左右，由此验证本文算法在节省计算时间上的确有较明显的优势。

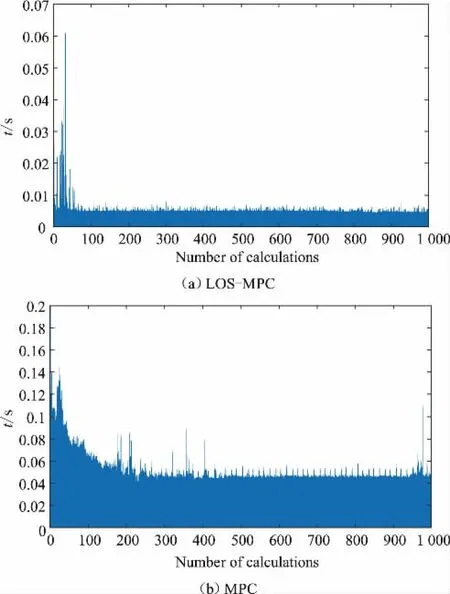
图8 本文算法与全MPC算法每轮计算时间对比

4 结语

本文针对大型欠驱动UUV设计了一种轨迹跟踪算法。首先对复杂问题进行分解，在大多数导航条件下只分析水平面。然后，将该问题解耦为运动学控制和动力学控制问题。对于运动学控制器，采用基于在Serret-Frenet坐标系中进行LOS角导航的虚拟制导方法；对于动力学控制器，采用模型预测方法设计水平路径跟踪控制器。通过与全MPC的控制效果比较，发现控制效果及计算时间均得到了改善。