基于交互多模型距离平滑的UWB/IMU因子图组合导航方法

李 旭，孔 鑫，刘锡祥,2，宋 翔，徐启敏

（1. 东南大学 仪器科学与工程学院，南京 210096；2. 微惯性仪表与先进导航技术教育部重点实验室，南京 210096；3. 南京晓庄学院 电子工程学院，南京 211171）

近年来随着交通系统的发展，对于高级驾驶员辅助系统（ADAS）、智能交通系统（ITS）等应用来说，获取精准可靠的车辆位置是至关重要的[1]。然而，现有的车辆高度依赖于GNSS技术，当车辆行驶至隧道、地下停车场等封闭区域时，由于卫星信号受到遮挡从而无法对车辆进行定位[2]。

当卫星信号不可用时，单一的惯性测量单元（IMU）无法对车辆进行精准的定位，可将IMU与其它传感器集成起来提高定位的精度[3]。目前，随着通信技术的发展，基于无线传感网络的定位技术受到了广泛关注。其中，UWB因其出色的穿透障碍物的能力和厘米级的测距精度而表现出高精度定位的巨大潜力。然而，由于交通场景的复杂性，无线信号会不可避免地产生反射和折射从而导致非视距效应，UWB的测距精度也会因此降低。为了解决UWB传输的非视距问题，文献[4]提出了自回归滑动平均模型来识别UWB的非视距测量量，然后引入模糊逻辑算法来自适应地调整对每个UWB测量量的依赖性。这类方法分类区间过于复杂，需要确定的参数过多，对非视距观测量的抑制效果不太明显。文献[5]利用无线信号的随机特征来检测非视距节点并将其删除，但容易造成可用节点过少，影响最终的定位精度。

在组合导航领域中，为了解决多传感器同步的问题，大部分方法都是采用传统的联邦卡尔曼滤波的方法[6]。这类方法通过数据同步处理能够融合不同频率的传感器，但却需要丢弃一部分测量值，从而造成信息的浪费。另一方面，虽然卡尔曼滤波在线性的情况下是最优的，但大部分传感器模型都是非线性的，在非线性的情况下扩展卡尔曼滤波边缘化所有过去状态仅估计当前状态来获取实时估计，在精度上有所下降[7]。其他的UKF[8]、PF[9]等滤波算法虽然具有较高的估计精度，但却是以复杂的运算量为代价的。

对于GNSS拒止环境下，基于UWB/IMU的车辆组合导航，经常会出现因非视距现象而出现的UWB测量值异常情况，以及传感器数据不同步的问题。针对上述问题，本文提出了一种基于UWB/IMU的“即插即用”因子图融合优化方法。基于因子图的算法能充分考虑历史测量信息，在定位精度上优于扩展卡尔曼滤波[10]，并且该算法能实现“即插即用”的功能，因为新的传感器只是添加到图中的新因子；同样的，若由于信号丢失或故障导致传感器失效，系统也会避免添加相应的因子。为了解决UWB信号非视距干扰的问题，本文在文献[11]建立的视距与非视距模型的基础上，提出了一种基于因子图的改进交互式多模型算法来抑制UWB的非视距误差，并将IMU输出的测量值与改进交互式多模型输出的多个UWB距离测量值添加到因子图模型中，从而形成一种即插即用的因子图组合导航方法。实车测试结果证明，所提出的方法能够兼容多个传感器信息，同时，该方法相较于传统的交互式多模型算法在定位精度上有所提升。

1 基于交互式多模型的距离平滑算法

1.1 UWB视距/非视距因子图模型

本文采用改进的交互式多模型算法对UWB原始距离测量值进行平滑，以减弱因非视距传播所导致的距离误差。由文献[11]可得，UWB距离的状态方程和观测方程为：

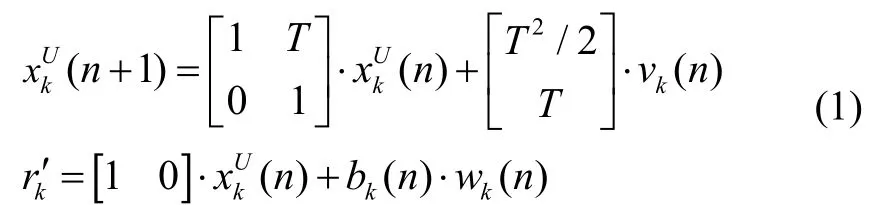
根据上述模型，即可建立相应的因子图模型，如图1所示。

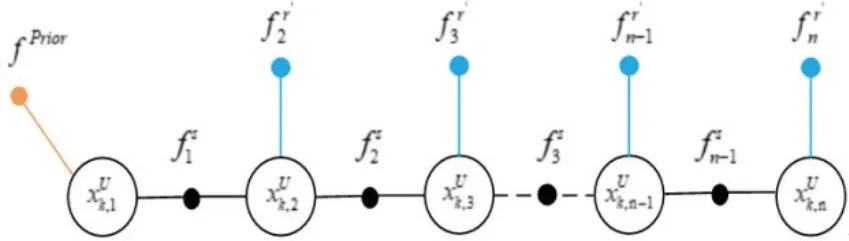
图1 基于因子图的UWB视距/非视距模型Fig.1 UWB LOS/NLOS model based on factor graph

在图1中，包含了一种变量节点和三种类型的因子节点。变量节点包括了车载标签与路侧第k个基站间的真实距离与相对速度，因子节点包括先验因子fPrior，状态转移因子 fs和距离因子 fr'。其中，先验因子的误差函数可表示为：

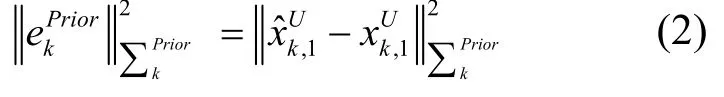
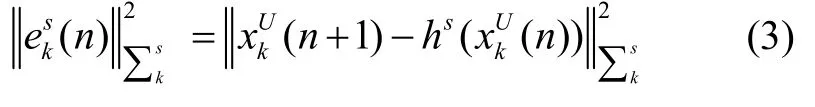
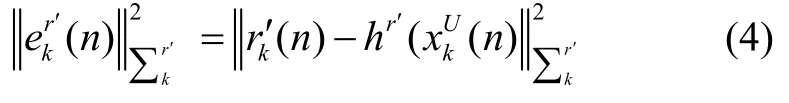
由建立好的因子图模型和误差函数方程，即可得到视距/非视距下的距离估计值，最终的目标函数为：

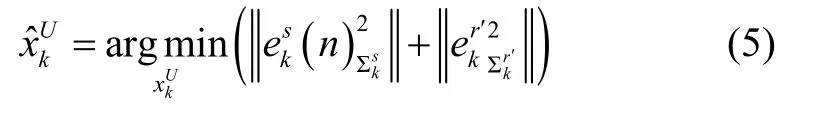
1.2 因子图模型的求解

对于1.1节的因子图模型，我们通过建立各因子的误差函数并把状态估计转换成基于最大后验估计的非线性最小二乘问题[11]：

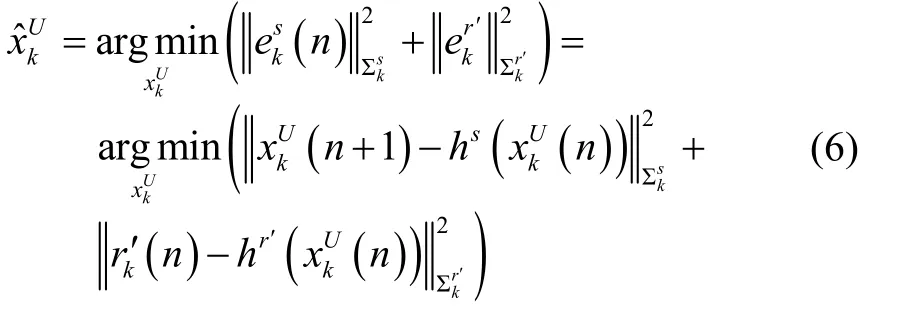
为了简单起见，在这里我们略去了之前的先验信息。通过对式(6)中的测量函数进行一阶泰勒展开来线性化，则状态转移因子的误差函数可进一步表示为：

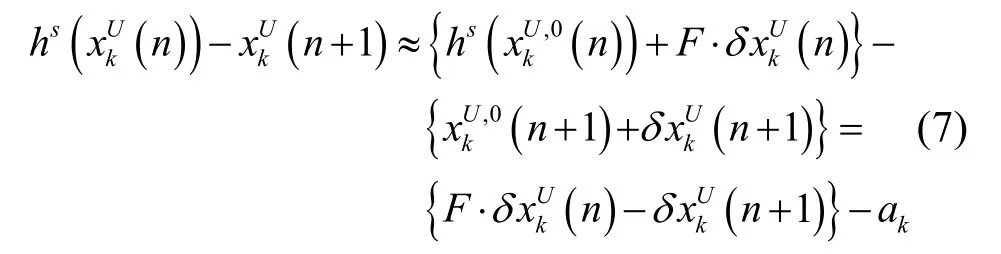
通过将误差函数线性化后，式(6)可转化为如下函数：

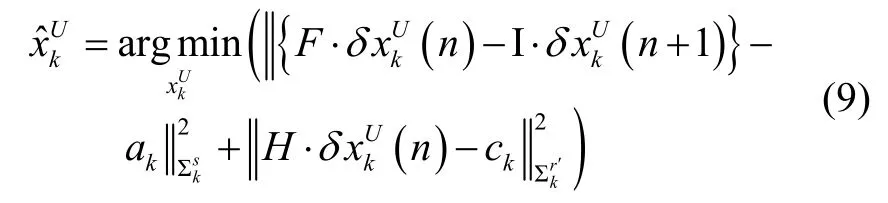
其中I为单位矩阵。通过马氏距离变换公式：

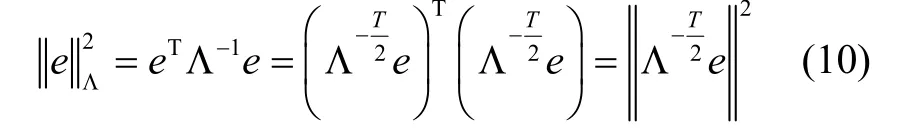
可以将式(9)的雅可比矩阵合并为一个大矩阵A，向量ak和ck合并到右侧向量b中，因此式(9)可转换为如下的标准最小二乘问题：

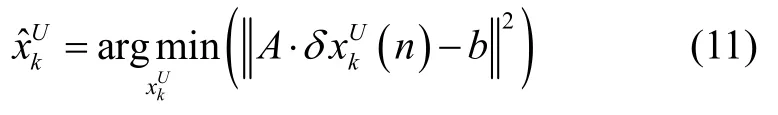
在数据量较大的情况下，式(12)可通过矩阵分解来求解。假设A可QR分解为A=QR，则有 QTA=[ R0]T且 QTb=[ d e]T。由于R为上三角矩阵，因此可通过回代法求得，则由线性化点更新得到的新的估计值为算法具体的求解过程可参考文献[11]。

1.3 改进的交互式多模型算法

在过去几年中，交互式多模型算法已经广泛地应用于车辆定位等领域[12,13]，在这类研究中，可能的状态变量由多个不同的模型表示，这些模型根据不同的条件建立。交互式多模型算法通过计算各个模型的权重值来获取最终的状态估计，因此具有自适应的特点。然而，传统的交互式多模型算法大多采用卡尔曼滤波来对模型进行估计，这类算法未能充分考虑历史观测信息，对视距/非视距模型不能起到较好的平滑作用。基于此，在1.1节建立的UWB视距/非视距因子图模型的基础上，本节提出了一种基于改进交互式多模型的距离平滑算法，如图2所示。

图2 改进的交互多模型框架与马尔可夫转换模型Fig.2 Improved interacting multiple model framework and Markov switching model

改进的交互式多模型距离平滑算法流程如下：

1）输入交互： ∀ i, j ∈［ 1 ,2］，1为视距模型，2为非视距模型， k∊［1 …K］。

混合权重：

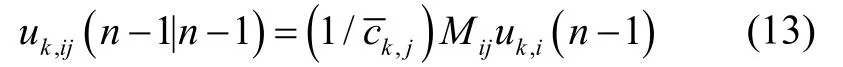
归一化因子：

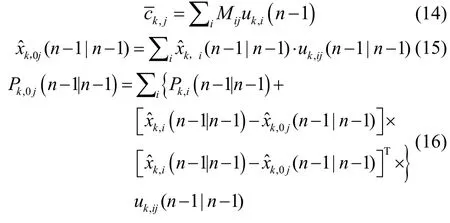
其中，Pk,i为第i个因子图模型输出的边缘化协方差矩阵。

2）因子图平滑：具体的因子图模型求解方法见第1.2节。

3）模型概率更新：似然函数为：

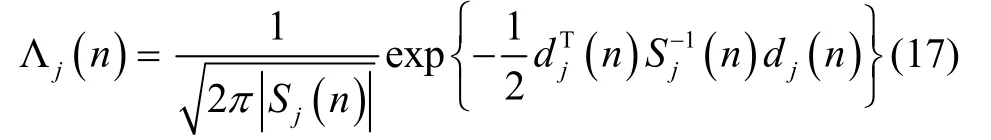
模型j的更新概率：

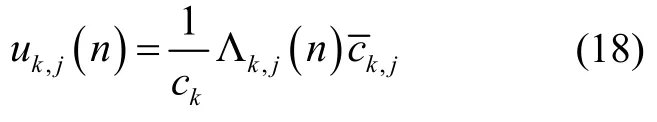
归一化常数：

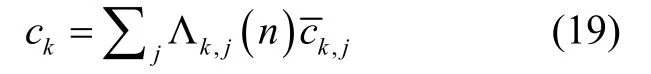
4）数据融合：

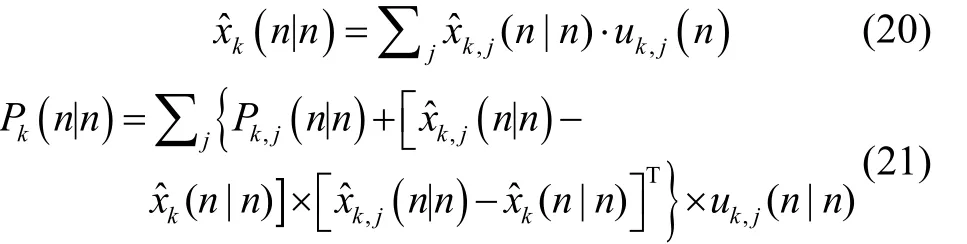
2 基于因子图的UWB/IMU融合框架

随着车载传感器的增加，传统基于滤波的方法不具备对异步导航信息即插即用的功能。因此，本文提出了一种基于因子图的多传感器融合方法，如图3所示。

在图3中，Xn和Vn分别代表n时刻车辆的位置和速度。其中，分别代表n时刻车辆的东向位置、北向位置和天向位置;分别代表n时刻车辆的东向速度、北向速度和天向速度。 fPrior代表先验因子， fMM代表运动模型因子， fv代表速度因子， fIMM代表交互多模型因子。

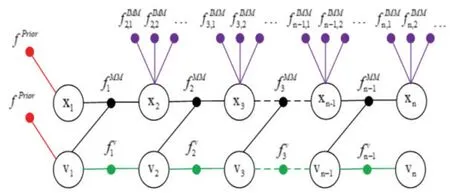
图3 基于因子图的UWB/IMU融合框架Fig.3 The framework of UWB/IMU based on factor graph

2.1 先验因子节点

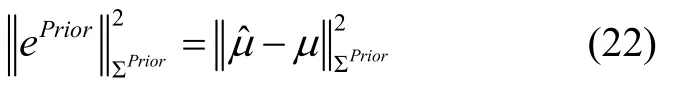
2.2 IMU因子节点

IMU因子包含了运动模型因子与速度因子，通过接收来自IMU的测量值定义这两种因子。其中， fb与 ωb分别代表载体坐标系下载体的比力和角速度。

因此，运动模型可表示为：

速度模型可表示为：

其中，ae、an、au分别为捷联惯导算法转换的载体在东北天坐标系的加速度。

则IMU因子的误差函数可表示为：

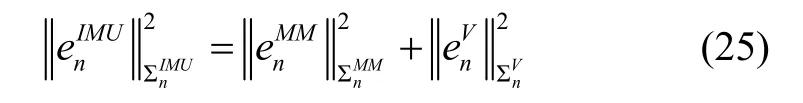
2.3 IMM因子节点

IMM因子的量测值来自交互式多模型输出的平滑后的UWB距离信息，因此IMM因子的量测方程可表示为：

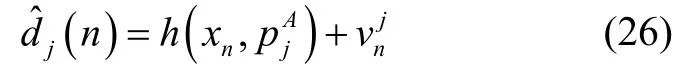
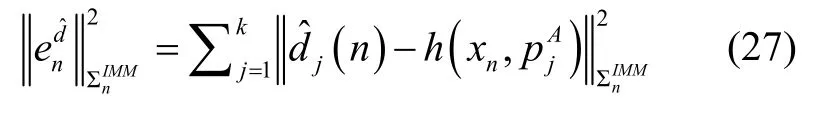
根据各传感器的工作频率实时地在因子图中插入相关的因子，根据各因子的代价函数实现变量的递推与更新。根据各传感器可用性的变化，最终实现车辆组合导航的“即插即用”。

3 实验结果与分析

本文开展了实际的实验测试，用于验证所提出算法的性能。测试系统包括采集频率为50 Hz的车载UWB标签、4个路侧UWB基站100 Hz的IMU和SCOUT 2.0移动机器人底盘。陀螺仪的零偏稳定性为0.3°/h，角度随机游走系数为0.05°/；加速度计的零偏稳定性为50gμ ，速度随机游走系数为0.01m/s/。

此外，考虑到在实际交通场景中进行实验存在一定安全隐患，且车辆实际运行过程中的参考轨迹难以获得，因此在测试平台上额外搭载了高精度的光纤组合导航系统KY-INS 300来作为运行轨迹的参考值。本文的实验场景为室外停车场，为了增加非视距效应，实验中人为地降低了UWB基站的高度。测试平台与实验场景如图4所示。

图4 测试平台与实验场景Fig.4 Experimental platform scene

在整个实验过程中，高精度的光纤组合导航系统仅作为参考值，并没有参与融合定位。根据不同时段UWB与IMU测量值的可用性，多源融合导航系统采用不同的传感器配置方案。我们分别对扩展卡尔曼滤波（EKF）、因子图（FG）、采用卡尔曼滤波的传统交互式多模型距离平滑的因子图（IMM-FG）以及本文提出的基于改进交互式多模型距离平滑的因子图（AIMM-FG）四种算法进行了对比。图5和图6分别展示了这四种算法的融合轨迹对比图以及欧氏距离误差对比图，表1罗列了这四种融合定位结果的欧氏距离误差统计数据，包括水平位置的均方根误差值和最大误差值。

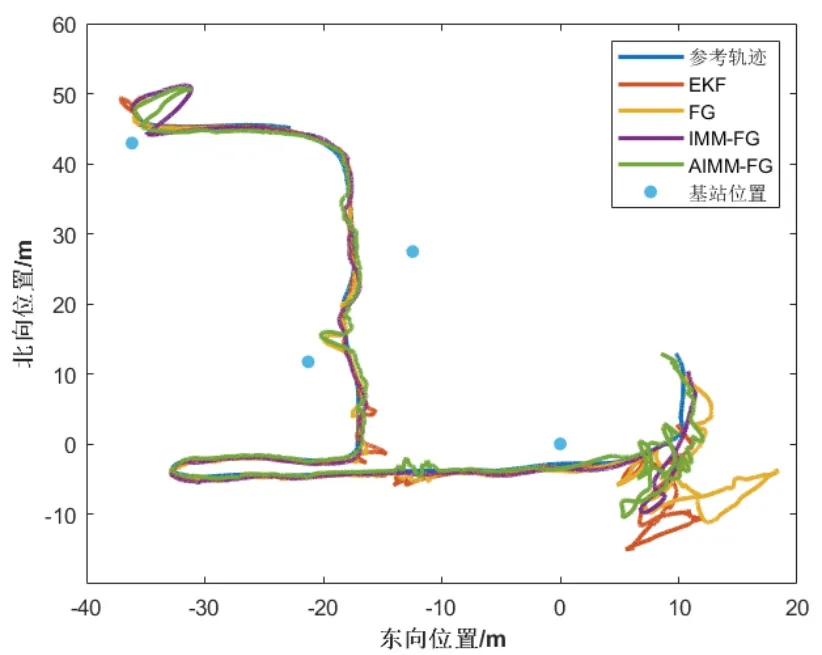
图5 融合轨迹对比Fig.5 Fusion trajectory comparison

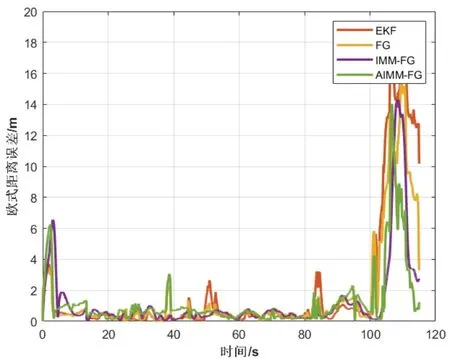
图6 欧氏距离误差对比Fig.6 Euclidean distance error comparison

表1 四种算法定位性能对比Tab.1 Positioning performance comparison of four algorithms

首先比较EKF和FG两种算法的定位效果，从图6和表1可以看出，EKF在水平位置上的最大误差和均方根误差分别为18.35 m和4.63 m，而FG在水平位置上的最大误差和均方根误差分别为15.82 m和3.53 m，相比于EKF误差分别下降了13.79%和23.76%。由此可见，FG算法由于充分考虑了历史测量信息，对UWB非视距误差的抑制效果更好，因此有着更高的定位精度。而在FG算法融合前首先对UWB原始测量信息进行抑制的IMM-FG和AIMM-FG算法在定位精度上又有了一定的提升。从表1可以看出，IMM-FG算法在水平位置上的均方根位置降到了2.81 m，相比于FG误差下降了20.39%；而AIMM-FG算法在水平位置上的均方根位置降到了2.32 m，相比于IMM-FG误差又下降了17.44% 。由此可见，本文提出的AIMM-FG算法相比于传统的IMM-FG算法对UWB的非视距误差有更高的抑制作用，较好地实现对车辆的精准定位。AIMM-FG算法比EKF算法在定位精度（RMS）上提升了40%以上。

图7 展示了四种算法的速度估计误差，从图中可以看出本文所提出的方法对车辆速度的估计具有更高的精度和更好的收敛效果。

图7 速度估计误差Fig.7 Velocity estimation errors

4 结 论

本文提出了一种基于交互多模型距离平滑的UWB/IMU因子图组合导航方法，该方法能够对UWB和IMU等传感器的非同步测量数据进行实时融合，从而实现传感器“即插即用”的功能。

首先，利用交互式多模型自适应的特性以及因子图算法能够充分考虑历史测量信息的特性，本文提出了一种改进的交互式多模型算法来对UWB原始测量值进行平滑，从而抑制非视距误差。其次，通过因子图融合交互式多模型输出的UWB距离信息与IMU测量值来达到异步传感器的实时融合，并在确保实时性的基础上进一步提升了定位精度。

本文在纯非视距情况下开展了实车测试，结果表明该方法能有效兼容各传感器的测量值，同时相比于EKF算法，本文的方法在定位精度（RMS）上提升了40%以上。