同轴旋拧可压缩气流中黏性液体射流稳定性
郭立梅,吕 明,宁 智
(北京交通大学 机械与电子控制工程学院,北京 100044)
目前,已有许多研究证实,同轴高速气流中的液体射流可以实现射流与周围气体的高效混合,与在静止气体中的液体射流相比,同轴射流的破碎方式更有利于雾化,并得到一些同轴气流式液体射流稳定性的研究成果[1-5].在射流的分裂与雾化过程中,往往伴随着周围气流的旋转[6-7],周围气流的旋转运动对射流的不稳定性有复杂的影响,逐渐成为研究的热点[8-13].Jog等[8]在不考虑气流可压缩性的前提下研究了周围气流的旋转运动.Lin等[9]在不考虑气流可压缩性的前提下研究了周围气流旋转运动对射流稳定性的影响.杜青等[11]研究了周围气流的旋转运动对环膜液体射流破碎的影响.Lü等[12]在不考虑气流轴向速度的前提下研究了气流旋转运动对射流稳定性的影响.这些学者都没有同时考虑周围气流的周向和轴向速度.
已有研究表明,液体黏度对射流稳定性的影响不容忽视.Decent等[14]研究了射流黏度对稳定性的影响,发现流体黏度对射流起致稳作用.Lin等[15]在考虑液体射流黏度的前提下,分析了不同液体黏度对射流稳定性的影响.另外,随着喷射压力的逐步提高,射流燃油及周围气体的可压缩对射流稳定性的影响变得日趋显著[1],严春吉[16]在不考虑周围气流旋拧作用的前提下,研究了射流黏度及气流可压缩性对射流稳定性的影响.
由于上述问题的复杂性,学者们在进行射流稳定性研究时,往往未将周围气流的旋拧作用(轴向和周向上的运动同时存在)、周围气流的可压缩性以及液体射流黏度的影响同时考虑.笔者在综合考虑周围气流的旋拧、可压缩性以及液体射流黏度的前提下,采用空间线性稳定性分析方法,推导了描述同轴旋拧可压缩气流中黏性液体射流稳定性的色散方程.在此基础上,研究气流旋拧对液体射流稳定性的影响,并进一步探讨流体物性对旋拧气流式液体射流稳定性的作用.
1 数学模型
1.1 物理模型与初始流场
考虑一束黏性液体射流通过半径为 a的圆形喷嘴喷射入同轴旋拧的可压缩气体介质中.图1所示将柱坐标系建立在喷嘴出口,射流方向与z轴方向相反.初始阶段,射流半径为 a,液体射流速度为 u1;周围气体在z轴速度为u2;绕z轴旋转强度为W0,即旋转角速度与射流半径平方的乘积.

图1 物理模型示意Fig.1 Physical model
针对上述射流的物理模型,作出假设是:(1)射流周围气体为可压缩的牛顿流体;(2)忽略射流周围气体的黏性、重力及温度对射流的影响;(3)液体射流无旋转,射流周围气体做同轴旋拧运动.
在图1所示的坐标系下,基于上述假设条件建立基本流场,即

1.2 数学模型的建立及求解
1.2.1 可压缩旋拧气流扰动控制方程
在考虑周围气体的可压缩性而忽略黏度及重力的条件下,气流满足连续性方程和Euler方程,有
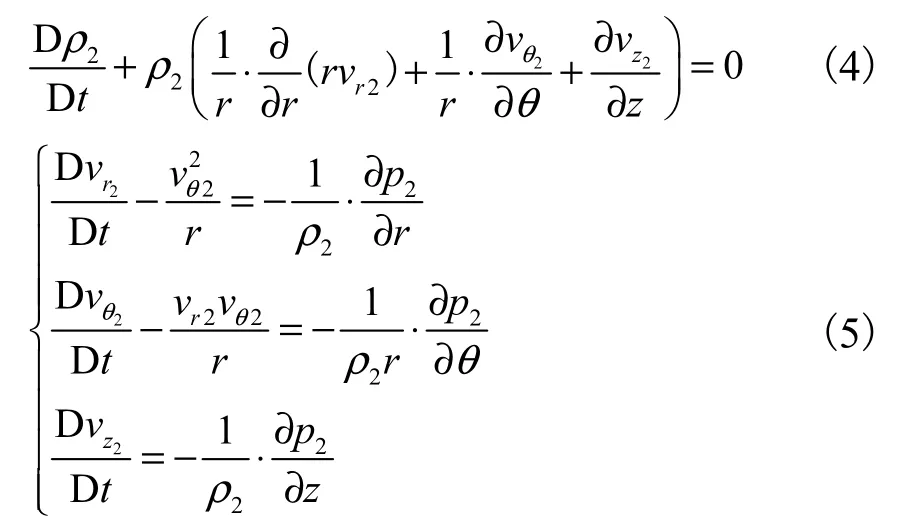
式中:下标2代表气流参数;vr、vθ和vz分别为径向、周向及轴向速度.
对式(4)和式(5)进行扰动分析并线性化,可以得到的射流扰动控制方程组为
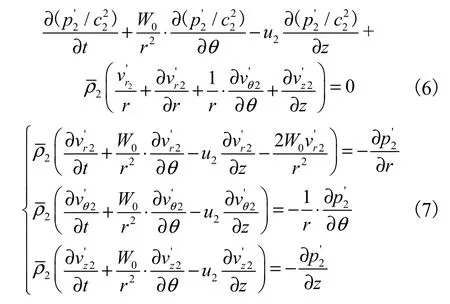
式中:上撇号表示小扰动参数.
式(6)~(7)包括 4个方程,但含有 5个未知数.为了使方程组封闭,利用将扰动密度和扰动压力与声速联系起来.至此,气流扰动控制方程组建立完毕.
1.2.2 黏性液体射流扰动控制方程
在考虑射流液体黏性、忽略可压缩性和重力的条件下,液体射流满足连续性方程和动量方程,即
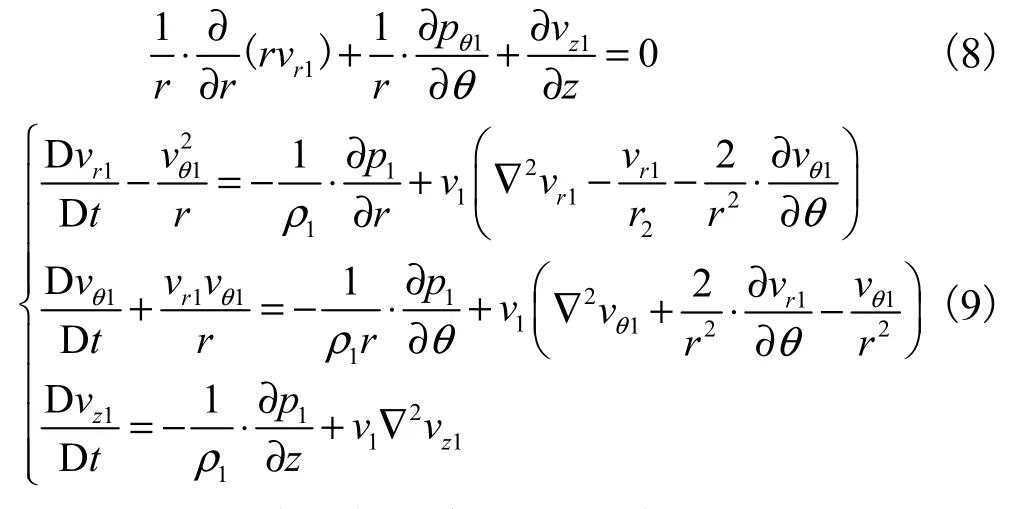
式中:下标1代表射流参数;ν1为射流动力黏度.
对式(8)和式(9)进行扰动分析并线性化,可以得到的射流扰动控制方程组为
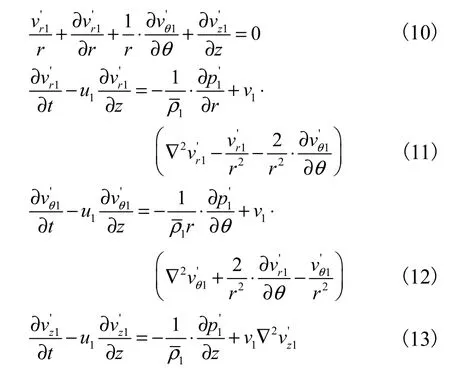
1.2.3 边界条件
在射流液体与周围气流的交界面上,控制方程的边界条件包括运动学和动力学边界条件,其公式为
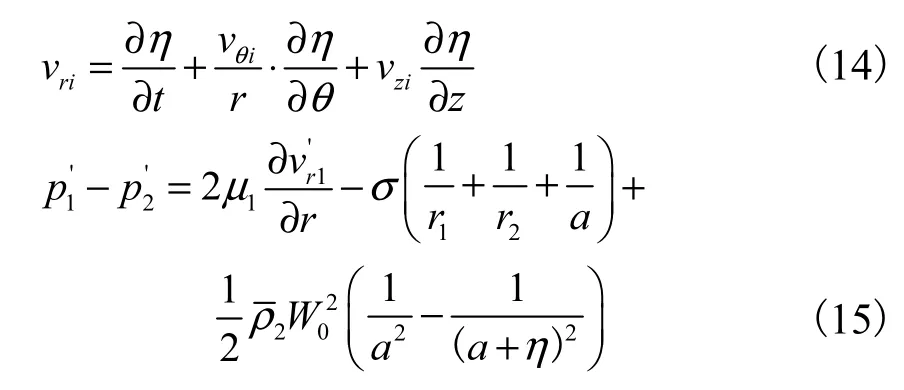
式中:下标 i=1、2,分别表示气流和射流参数;η为分界面上射流所受扰动;μ1为射流运动黏度;r1和 r2分别为分界面上液相和气相的主曲率半径.
对式(14)、式(15)进行扰动分析并线性化,可以得到形式的边界条件为
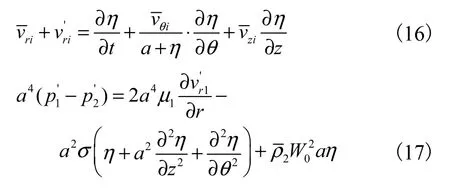
1.2.4 色散方程
联立射流扰动控制方程组和边界条件得式(18).

式中:X=[a11,a12,d11,d22,η0]T;A 为一个包含 k、ω、m及其他射流参数的5×5系数矩阵.
方程组(18)存在非零解的条件是:系数矩阵的行列式为零,由此可得:

式(19)即为建立的描述同轴旋拧可压缩气流中黏性液体射流稳定性的色散方程.
鉴于方程的复杂性,给出简写形式为
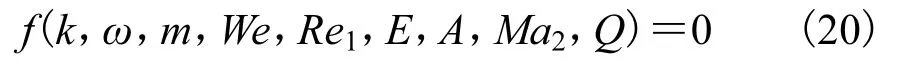
式中:k =kr+i ki,其中,kr为z方向波数,与波长λ的关系为 kr=2πa/λ,ki为扰动空间增长率;ω=ωr+iωi,其中,ωr为扰动时间增长率,ωi为波频;实数 m是角向模数,表示射流扰动在周向方向的形态,根据m数值可以将射流扰动分为轴对称扰动(m=0)和非轴对称扰动(m≠0);We为韦伯数倒数,W e=σ/为射流雷诺数,R e1=u1a/v1;E为量纲为 1旋转强度,E=W0/(u1a);A为气/液轴向速度比,A=u2/u1;Ma2为气体马赫数,Ma2=u2/c2;Q为气/液密度比
在色散方程式(20)中实际上含有11个参数(k和ω 均为复参数,即这两个参数含有 4个未知数);除去 6 个射流参数(We,Re1,E,A,Ma2,Q)及角向模数m可以给定外,式(20)中仍有 4个待定参数(k和 ω的实部及虚部).而为了满足方程可解条件(实部和虚部各含一个方程),色散方程中的未知参数个数最多只能有两个.基于此,采用空间模式进行研究.
1.3 数学模型的验证
若只考虑轴对称扰动时无黏射流射入无旋拧且不可压缩气体内的情况,即 m=0、Re1=0、E=0、A=0及Ma2=0,则色散方程式(20)退化为
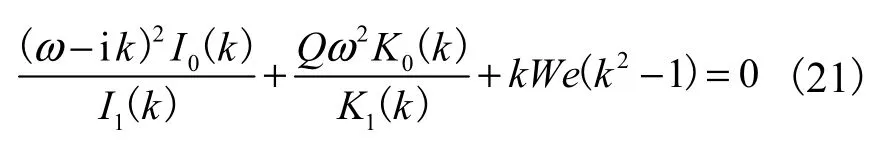
退化后的色散方程式(21)与 Lin等[15]推导的描述轴对称扰动时相同条件下液体射流稳定性的色散方程相同.若仅仅忽略射流周围气体的可压缩性,即Ma2=0,则色散方程(20)退化为
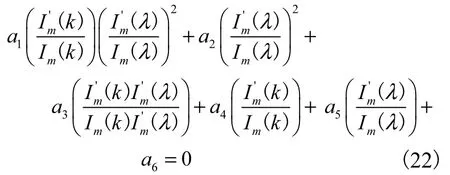
退化后的色散方程式(22)与 Lin[17]推导的描述相同条件下液体射流稳定性的色散方程一致;两者形式上的不同是由于坐标系中轴向方向及波频的定义不同造成的.
上述两种特定情况下的比较可以从一定程度上说明色散方程的正确性.为了对数学模型及数值求解方法进行验证,采用文献[15]中的算例参数进行计算,并与文献中给出的结果进行对比,结果如图2所示.利用笔者的色散方程求解方法得到的计算结果与文献[15]提供的原始数据基本吻合,可以证明求解的正确性.两条曲线存在一定的偏差是由于在求解方程时采取的方法不同:笔者采用弦截法,文献[15]采用穆勒法.
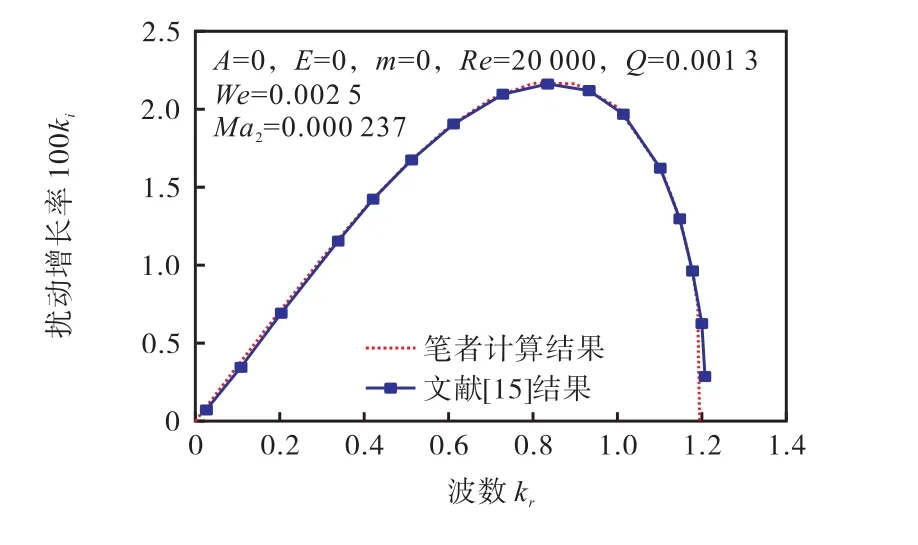
图2 计算结果与文献数据的比较Fig.2 Comparison of calculation results with data in reference
2 比较与分析
建立的数学模型可以同时体现周围气流旋拧速度和可压缩性、射流黏性以及表面张力对旋拧气流式液体射流稳定性的影响.在对射流稳定性问题的分析时,将柴油作为射流液体,采用的相关参数如表1所示.

表1 计算参数Tab.1 Calculating parameters
2.1 气流旋拧对射流稳定性的作用
在研究周围气流的速度引起的气动干扰作用对射流稳定性的影响时,采用气/液轴向速度比 A=u2/u1来表征气流轴向引射速度;采用气流量纲为 1旋转强度 E=W0/(u1a)来表征射流周围气流的旋转速度.将气流旋拧运动分为气流轴向引射对旋拧气流式液体射流稳定性的作用和气流旋转对旋拧气流式液体射流稳定性的作用.
2.1.1 气流轴向引射对射流稳定性的作用
根据气/液轴向速度比 A的大小将气流的轴向引射作用分为弱引射(A≤2)和强引射作用(A>2).图3给出了周围气流存在旋转速度(E=1)、周围气流弱轴向引射作用(A≤2)下射流表面扰动空间增长率随轴向波数变化的比较.在弱引射范围内,当射流周围气体引射速度增大时,扰动增长率并不是线性增大:气/液轴向速度比A从0增大到2时,射流扰动增长率先减小后增大,当气/液轴向速度相等即 A=1时,扰动增长率最小,此时射流最稳定;在A=2时,射流的扰动增长率和气流静止即A=0的情况下是基本相等的;同样观察到A=0.5与A=1.5时扰动增长率曲线基本重合.可以得出这样一个结论:气/液速度比A-1的绝对值相同时,即气/液轴向速度差相等,产生的空气动力学作用对射流稳定性的影响基本相同.在此区域内,气流的引射作用会抑制旋拧气流式液体射流的雾化分裂.
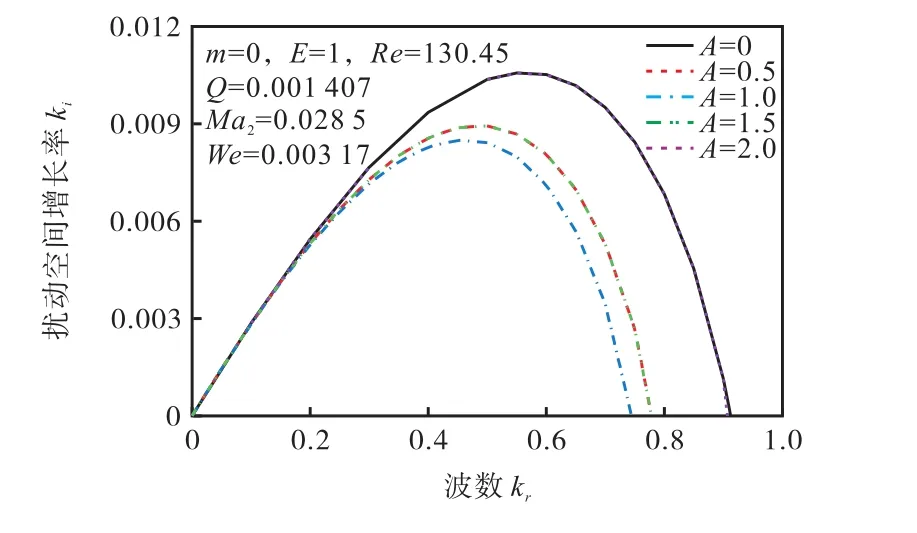
图3 弱引射作用下扰动增长率随轴向波数的变化比较Fig.3 Comparison of the variation of disturbance growth rate versus axial wave numbers under weak ejection
图4给出了周围气流存在旋转速度(E=1)、周围气流强轴向引射作用在轴对称扰动(m=0)和非轴对称扰动(m=1,2,3)下射流表面扰动空间增长率随轴向波数变化的比较.从图4a中可以看到,强引射范围内,在轴对称扰动下,射流周围气流的轴向引射有利于同轴旋拧气流式液体射流的失稳分裂.增大气流轴向引射作用(A>2),各轴向波数下的扰动空间增长率均增大,且轴向引射速度越大,扰动空间增长率增大得越明显,不稳定轴向波数范围明显拓宽.
由图4可知,轴对称和非轴对称模式下的气流轴向引射对旋拧气流式液体射流稳定性的影响规律是一样的.无论周围气流轴向引射速度多大,轴对称扰动下的射流扰动空间增长率始终大于非轴对称扰动下的射流扰动空间增长率.这说明周围气流的轴向引射速度不会改变射流轴对称扰动占优模式.
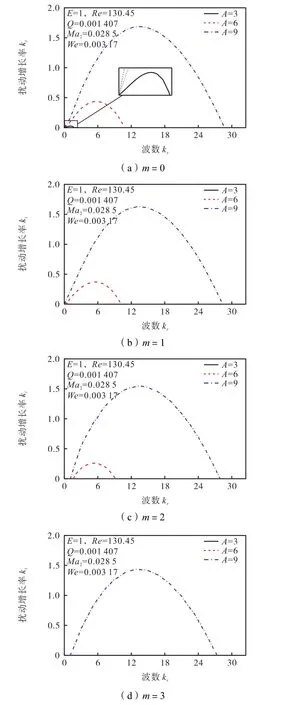
图4 强轴向引射下射流表面扰动增长率随轴向波数的变化Fig.4 Variation of disturbance growth rate versus axial wave numbers under strong axial ejection
2.1.2 气流旋转对射流稳定性的作用
图5给出了周围气流存在轴向引射速度(A=9)、周围气流有无旋转速度在两种扰动形式下射流表面扰动空间增长率随轴向波数变化的比较.从图5a中可以看到,在轴对称扰动下,射流周围气流的旋转不利于同轴旋拧气流式液体射流的失稳分裂.增大气流量纲为1旋转强度E,各轴向波数下的扰动空间增长率均减小,且旋转强度越大,扰动空间增长率减小得越明显,不稳定轴向波数范围明显减小.
由图5可知,无论周围气流旋转速度多大,轴对称扰动下的射流扰动空间增长率始终大于非轴对称扰动下的射流扰动空间增长率,随着角向模数 m的增大,射流稳定性增强.这说明周围气流的旋转速度不会改变射流轴对称扰动占优模式.
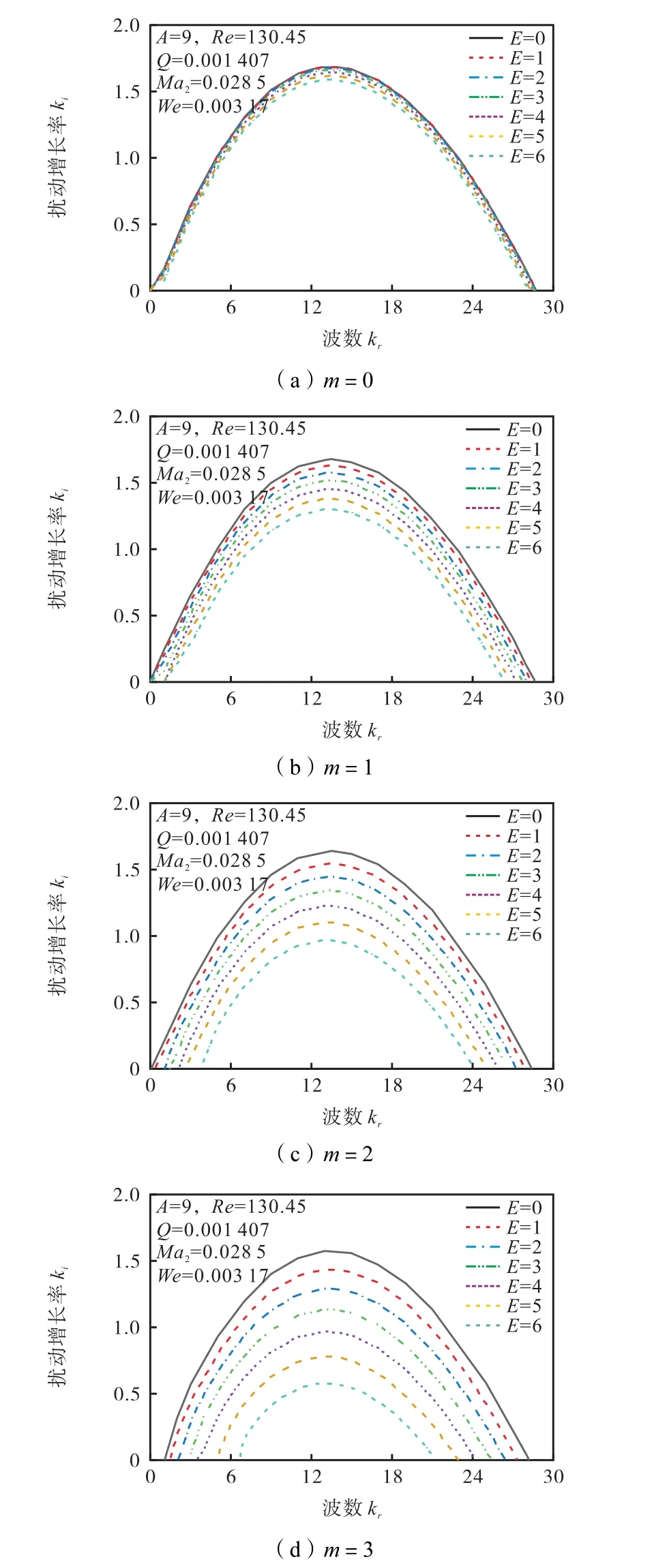
图5 不同旋转速度下射流表面扰动增长率随波数的变化Fig.5 Variation of disturbance growth rate versus axial wave numbers under different swirling velocities
为进一步探讨周围气流轴向与周向两种速度耦合作用对不稳定性的影响,计算得到不同气/液轴向速度比、气流周向量纲为1旋转强度条件下的最大扰动增长率见图6.选择的气/液轴向速度比A∈[0,3],气流量纲为1旋转强度E∈[0,2].
通过观察图6并结合计算得到的数据可以得到,气流轴向引射速度与液体射流速度相等,即 A=1是一个关键点.在气流轴向引射速度小(A<1)时,气流的旋转对射流存在稳定性作用,且旋转速度从某一值开始增大,射流容易失稳;给定周围气流旋转速度,气流的轴向引射速度增大,射流扰动增长率随之减小.在气流轴向引射速度大(A≥1)时,气流的旋转速度对射流始终呈现稳定的作用;而给定周围气流旋转速度时,增大气流引射速度,射流容易失稳.

图6 气流轴向与周向速度耦合作用对不稳定性的影响Fig.6 Effects of the airflow axial and swirling velocities on jet instability
2.2 流体物性对射流稳定性的影响
综合两种气流旋拧情况可知,气流旋转不利于旋拧气流式液体射流的失稳分裂,而增大气流的轴向引射速度则有利于射流的失稳分裂.因此,将对给定周围气流旋转速度下的气流旋拧式液体射流进行稳定性分析.
2.2.1 气体可压缩性的影响
随着射流喷射压力提高,流体可压缩性对射流稳定性的影响变得显著.由于液体射流密度较大,可压缩性可忽略不计,故只针对周围旋拧气流的可压缩性对射流稳定性进行分析.
由于在建立色散方程时,对气流马赫数 Ma2=u2/c2的定义是以气流轴向引射流速度为基准,而尚未考虑气流的旋转速度.故定义一个量纲为 1参数Ma2′=W0/(ac2)进行计算分析,Ma2′为周围气流旋转速度与声速之比,更准确地表征不同气流量纲为1旋转强度下气流可压缩性的大小.
图7a和图7b给出了周围气流轴向引射速度A=5时周围气流的可压缩性对旋拧气流式液体射流稳定性影响的计算结果;图7c和图7d给出了周围气流轴向引射速度A=6时周围气流的可压缩性对旋拧气流式液体射流稳定性影响的计算结果.无论轴对称扰动还是非轴对称扰动,周围气流作旋拧运动时,随着气体可压缩性的增大,各轴向波数的扰动空间增长率均增大,支配波数也增大,这说明气体可压缩性对射流起不稳定作用.气体可压缩性大小不会改变射流扰动占优模式,轴对称扰动下的最大扰动空间增长率始终大于非轴对称扰动下的最大扰动空间增长率,轴对称扰动占优.对比图7a和图7c发现,增大周围气流的轴向引射速度 A,气体可压缩对旋拧气流式射流稳定性的影响规律一致,但轴向引射速度大的射流,其增大气体可压缩性对应的扰动空间增长率增长幅度大,这说明周围气流轴向引射速度越大,气体可压缩性对旋拧气流式液体射流稳定性影响越强,气体可压缩性越不能忽略.
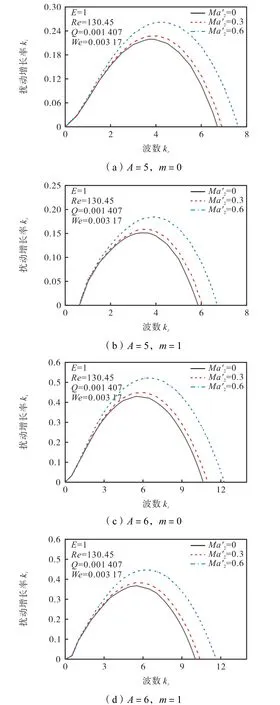
图7 周围气体可压缩性对旋拧气流式液体射流稳定性影响的比较Fig.7 Effects of the airflow compressibility on jet stability in a coaxial twirling gas
周围气体可压缩性对射流表面不稳定扰动起到增长作用的主要原因可能是气体可压缩性会影响气相压力脉动,可压缩性越强越促进射流表面扰动发展;而周围气流速度的出现和变化是压力脉动产生和变化的基本条件和决定性因素,增大周围气流速度增加了压力脉动产生,故对较高的气流轴向引射速度,气体可压缩性能更加剧射流的失稳破碎.
2.2.2 液体黏性的影响
根据雷诺数的定义 R e1= u1a /v1,当液体射流速度一定时,可用来表示射流黏性大小,射流黏度与雷诺数呈反比关系,当射流黏度增大时,雷诺数减小.
图8给出液体黏性在轴对称扰动(m=0)和非轴对称扰动(m=1)下对旋拧气流式液体射流稳定性影响的比较.在周围气流做旋拧运动时,液体黏性在轴对称扰动和非轴对称扰动下的影响规律是一样的.各轴向波数对应的扰动空间增长率和支配波数均随雷诺数的增大而增加,而截止波数基本不发生改变.根据角向模数一致时,液滴粒径与波数呈反比的关系可知[15],液体黏性对旋拧气流式液体射流起促稳作用;液体黏性减小,射流失稳分裂后得到的液滴粒径总体减小,而分裂得到的最小液滴粒径大小基本一致.
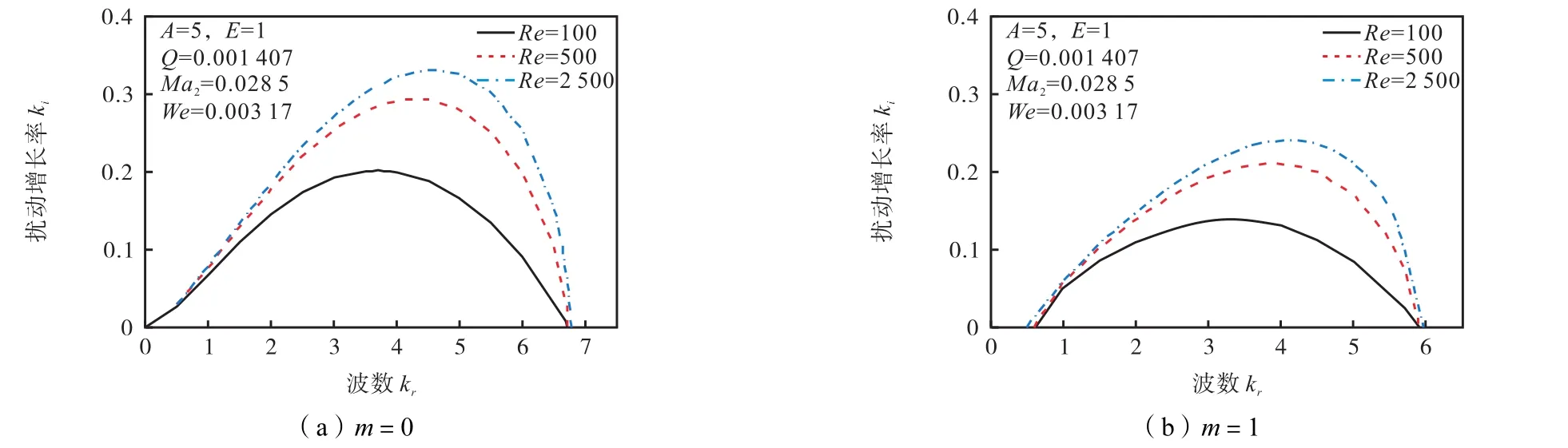
图8 轴对称和非轴对称扰动下液体黏性对射流稳定性影响Fig.8 Effects of liquid viscosity on the jet stability under the axisymmetric and asymmetric disturbance
图9为轴对称扰动下液体黏性在不同轴向引射强度下对旋拧气流式液体射流稳定性影响.随着动力黏性的增大,射流最大扰动空间增长率一直减小,且减小的趋势先显著后平缓,说明在一定黏性范围内,黏性对射流的稳定性起明显的促稳作用,当黏性过大时对稳定性影响效果略微.对比气/液轴向速度比A为 3、4和5对应的3条曲线可知,增大气流轴向引射速度,最大扰动空间增长率的曲线更陡,说明周围气流轴向引射速度增大后液体黏性对旋拧气流式液体射流稳定性的影响更显著.
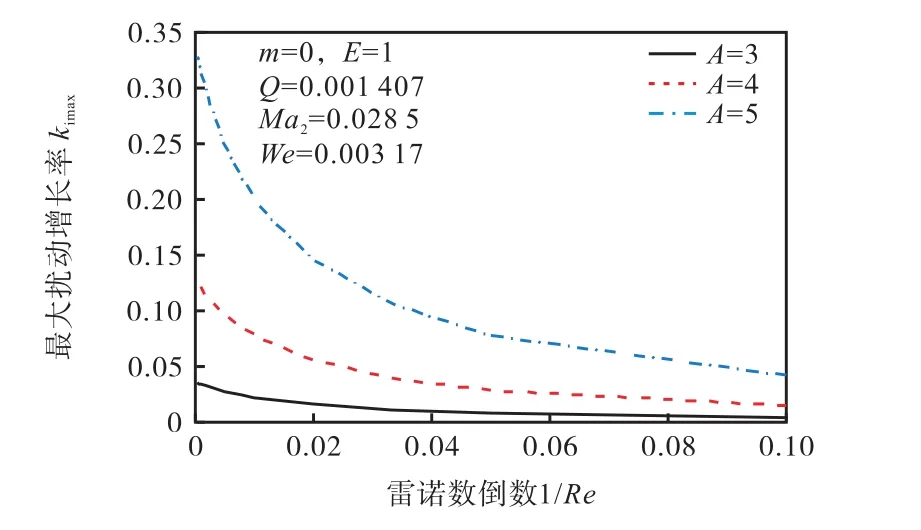
图9 不同轴向引射下液体黏性对射流稳定性的影响Fig.9 Effects of 1/Re on the stability of liquid jet in coaxial twisting gas under different ejection strength
2.2.3 气/液密度比的影响
在射流的失稳分裂问题中,一般以气/液密度比来表征气动力的大小.为探讨气动力对轴向引射射流稳定性的影响,图10为气/液密度比Q在轴对称扰动(m=0)和非轴对称扰动(m=1)下对旋拧气流式液体射流稳定性影响的比较.无论在轴对称扰动还是非轴对称扰动下,在周围气流做旋拧运动时,各轴向波数对应的扰动空间增长率和支配波数均随气/液密度比的增加而增大,不稳定轴向波数的范围明显拓宽.这说明气/液密度比对旋拧气流式液体射流的分裂雾化起促进作用.对比图10a和图10b可知,气/液密度比相等时,在轴对称扰动下对应的扰动空间增长率明显大于非轴对称扰动,说明在计算参数下射流表面轴对称扰动占优.
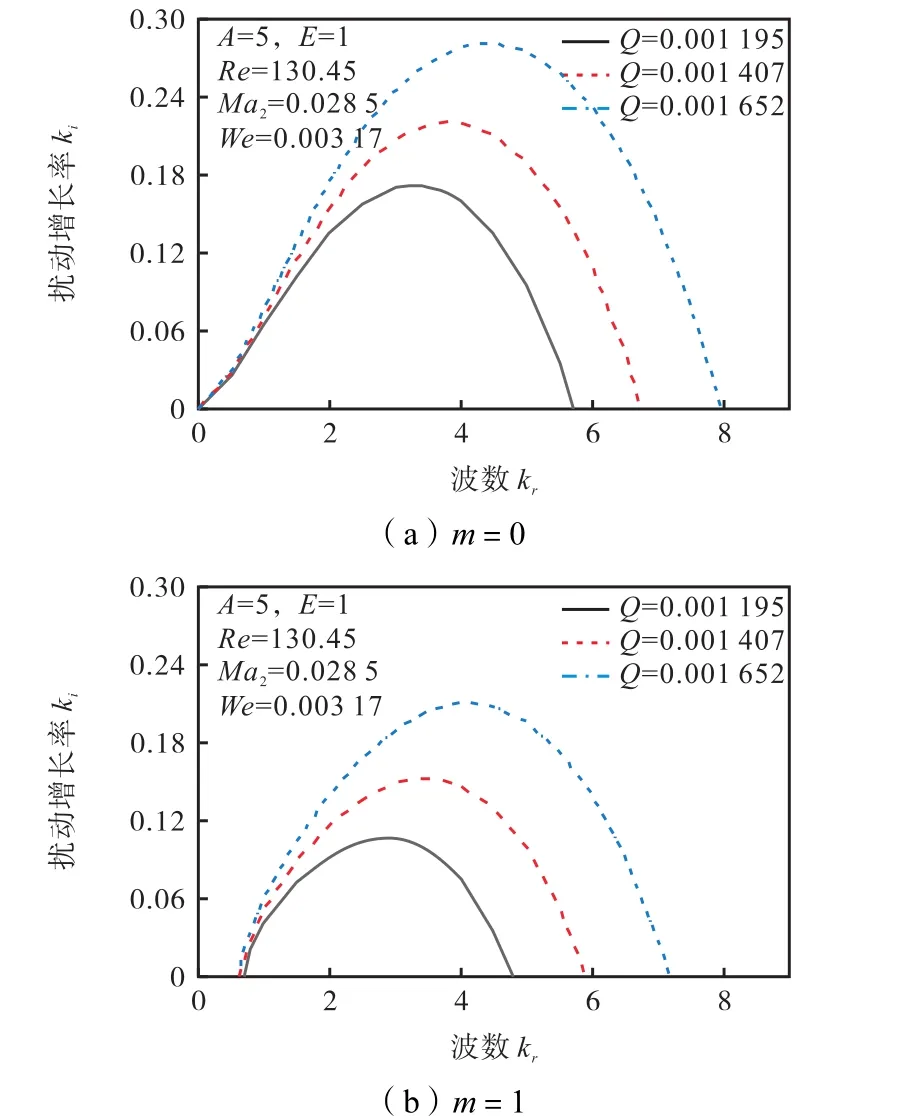
图10 轴对称和非轴对称扰动下Q对射流稳定性影响Fig.10 Effects of Q on the jet stability under the axisymmetric and asymmetric disturbance
图11为气/液密度比在不同气流轴向引射强度下对旋拧气流式液体射流稳定性影响的比较.在周围气流做旋拧运动时,周围气流轴向引射速度从 A=3增大到 A=5,最大扰动空间增长率的曲线斜率明显增大,说明周围气流轴向引射速度增大后气/液密度比对旋拧气流式液体射流稳定性的影响更显著.且各气/液密度比对应的最大扰动增长率依次增大,这说明气/液密度比没有改变气流轴向引射对旋拧气流式液体射流的促分裂作用.

图11 气/液密度比在不同气流轴向引射强度下对液体射流稳定性影响的比较Fig.11 Effects of gas-liquid density ratio on the stability ofliquid jet under different ejection strength
2.2.4 表面张力的影响
We=表征表面张力与惯性力的相对大小,故利用We反映表面张力的大小.图12为表面张力在轴对称扰动(m=0)和非轴对称扰动(m=1)下对旋拧气流式液体射流稳定性影响的比较.周围气流做旋拧运动时,韦伯数倒数 We∈[0.002,0.004]时,表面张力增大,各轴向波数对应的扰动空间增长率随之减小,不稳定轴向波数范围减小,这说明表面张力在此范围内,对旋拧气流式液体射流起稳定性作用,增大表面张力,不利于射流的失稳分裂.改变表面张力大小,在轴对称扰动下的最大扰动空间增长率比非轴对称扰动下大,说明表面张力不会改变射流表面扰动占优模式,始终为轴对称占优.
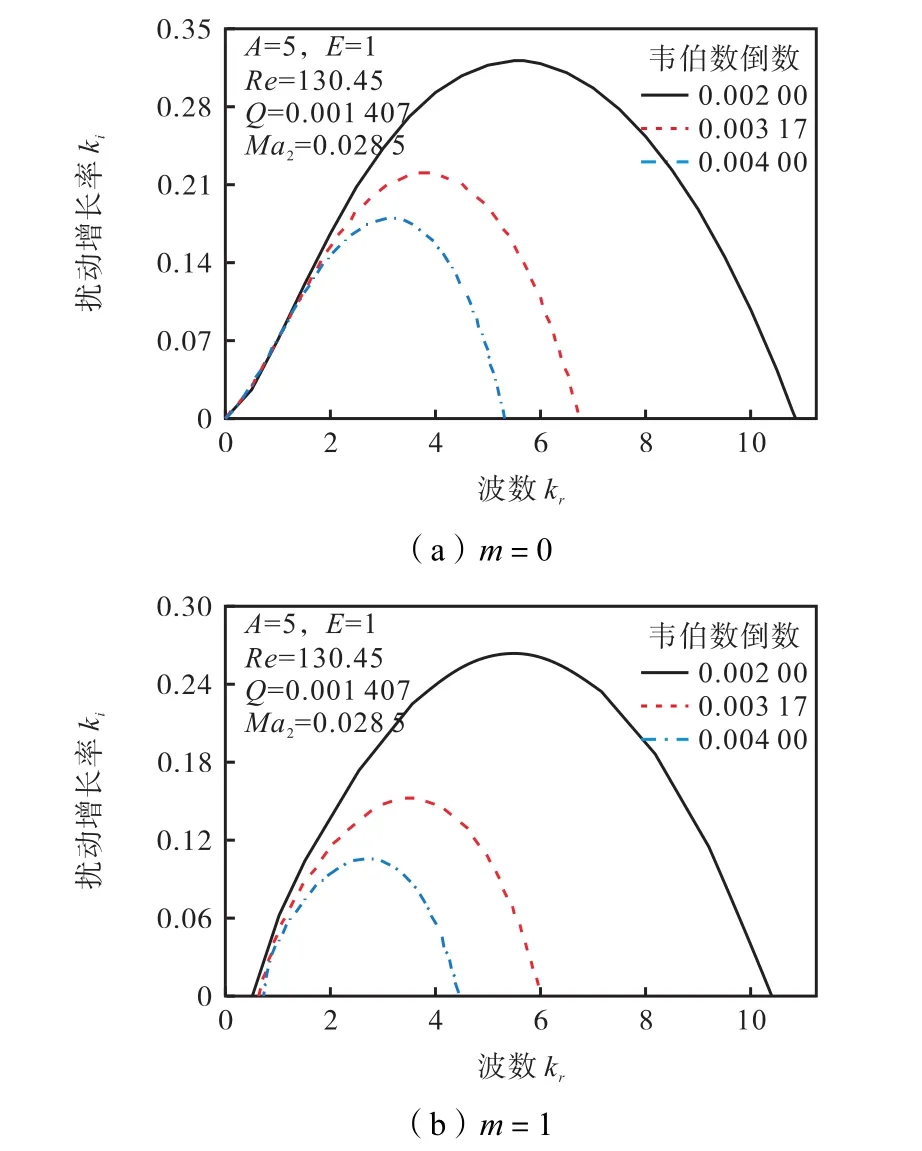
图12 轴对称和非轴对称扰动下表面张力对射流稳定性影响Fig.12 Effects of surface tension on the jet stability under the axisymmetric and asymmetric disturbance
为探讨表面张力对不同气流引射作用下旋拧气流式液体射流稳定性的作用,图13为不同气流轴向引射强度下表面张力对旋拧气流式液体射流稳定性影响的比较.在不同韦伯数倒数下,对射流破碎的影响程度不同.对不同气流轴向引射作用下,最大扰动空间增长率随韦伯数倒数的增大先极速减小后缓慢增大,说明随着表面张力的增大,旋拧射流的稳定性先增大后减小.且对稳定性的作用在表面张力较小时变化明显,增大到一定程度后,影响效果减小,但由于表面张力较大时对射流起的失稳作用较微弱,很难达到表面张力较小时的最大扰动空间增长率,故表面张力较小时是射流破碎的驱动因素,表面张力较大时,称为射流的稳定因素.
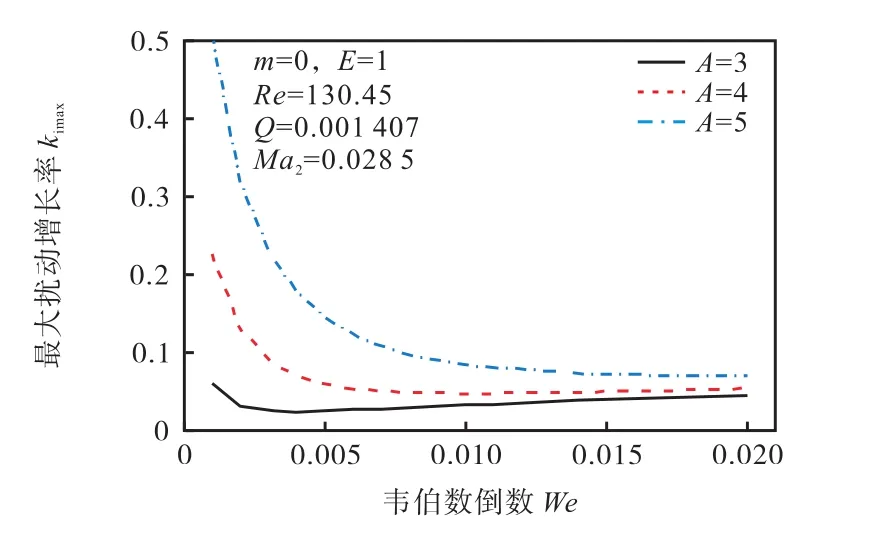
图13 不同气流引射强度下表面张力对液体射流稳定性的影响Fig.13 Effects of surface tension on the jet stability under different airflow ejection strength
对比图13中周围气流轴向引射速度 A为 3、4和5的3条曲线,各表面张力对应的最大扰动增长率依次增大,这说明表面张力没有改变气流轴向引射对旋拧气流式液体射流稳定性的作用,不同的表面张力下,气/液轴向引射速度对旋拧气流式液体射流始终起促分裂作用.
3 结 论
(1) 基于线性稳定性理论分析方法,在同时考虑周围气流旋拧运动及可压缩性、射流液体的黏度的条件下,建立了描述同轴旋拧可压缩气流中黏性液体射流的数学模型,并对数学模型以及求解方法进行了验证分析.
(2) 周围气流做旋拧运动时,弱引射范围内(A≤2)旋拧射流不稳定性随气/液轴向速度比的增大先减小后增大;强引射范围(A>2)内气流的轴向引射速度增大,各轴向波数对应的扰动增长率均明显增大,对射流的失稳分裂有明显的促进作用;周围气流与射流之间轴向速度差与气/液间空气动力学作用呈正比关系,速度差越大,空气动力作用越强,射流越不稳定;而气流旋转速度的增大令各轴向波数对应的扰动增长率减小,对射流有促稳作用,不利于射流的分裂雾化;两种情况下,射流均以轴对称扰动占优.
(3) 周围气流做旋拧运动时,气体可压缩性、液体黏度、气/液密度比及表面张力均不会改变射流扰动占优模式且不会改变周围气流的轴向引射作用对旋拧气流式液体射流稳定性影响规律;其中,气体可压缩性和气/液密度比对旋拧气流式液体射流起促分裂作用;液体黏度起促稳作用,但液体黏度对射流破碎后的液滴粒径影响很小;表面张力的增大对射流不稳定性有先极速减小后缓慢增大的作用,表面张力较小时对射流失稳有意义,表面张力的转捩点也随气流轴向引射速度增加而增大;这些流体物性均在较大的气流轴向引射速度下,对旋拧气流式液体射流稳定性的影响较大.

