船用低速柴油机喷嘴内流及初次破碎机理研究
潘业俊,刘灿旭,刘 红,尹洪超
(大连理工大学 海洋能源利用与节能教育部重点实验室,辽宁 大连 116024)
船舶推进系统的效率随其转速的增加而降低,因而现代船舶普遍采用大型低速柴油机作为主推进动力装置以降低油耗.而柴油机虽具有低油耗、经济适用和大转矩等优点,但燃烧带来的污染排放仍对环境造成了不可逆的影响.燃烧性能与燃油雾化质量息息相关,喷嘴喷出的燃油油滴越细小和均匀越有利燃油蒸发和快速燃烧.现代柴油机普遍使用小孔径和高喷射压力以获得更好的雾化效果,而船用柴油机的大流量需求使其无法通过缩小孔径来实现高质量油、气混合气的形成.因此,如何强化船用柴油机喷嘴雾化性能,促进油、气混合从而优化燃烧面临着极大的挑战.为实现此目的,必须深入探析其喷雾雾化机理.
在长期的喷雾研究中,学者们已经提出了多种关于雾化机理的理论假说[1].空气动力干扰说认为射流表面的不稳定波是由液体与空气的相互干扰引起的;湍流扰动说认为液体湍流特别是喷嘴出口处的湍流对雾化破碎起重要作用;空化扰动说认为喷孔内的空化造成的压力波动才是雾化的主要原因.研究表明,喷孔内部空化气泡的溃灭在对喷嘴结构造成侵蚀的同时所带来的能量扰动对下游喷雾特性有着一定程度的影响[2-4].燃油离经喷孔之后首先发生初次破碎,这是液柱在气动力作用下失稳致使大量的液带和液滴从射流表面剥离的过程.初次破碎在一定程度上控制着液体核心的长度,并为后续分散流中的二次破碎提供初始条件,在整体的雾化进程中占据着举足轻重的地位[5-7].
目前,喷孔内流及近场喷雾特性的研究[8-10]多采用孔内模拟、孔外试验二者相结合,或进行整体可视化试验的方法,前者容易产生较大的数值误差,后者受限于材料和尺寸多采用不符合实际燃油喷射系统的低喷油压力.因此,为更好地揭示上述 3种影响因素对船用低速柴油机近场喷雾特性的影响规律,笔者基于 OpenFOAM 平台,采用自搭建的多流体-准VOF模型,应用气-液相间动量交换模型考虑气动力对雾化的干扰,大涡模拟求解混合流体的湍流方程以探析湍流对雾化破碎的作用,耦合修正的空化子模型将空化扰动对初次破碎的影响亦纳入考虑范畴,在接近实际运行工况的高喷射压力和高环境压力条件下,对某船用低速柴油机喷嘴展开深入的孔内流动和初次破碎的耦合研究,在探明其雾化特性的同时给出一种在实际工况中较传统VOF模型更为精准的数值计算模型.
1 数学与物理模型
在欧拉多流体模型中各相首先满足基本守恒方程,包括流体动力学特性方程以及能量方程.喷孔内流和近场射流在实际过程中热交换量很小,因而研究不考虑能量方程;其次,在计算流体动力学(CFD)数值模拟过程中,湍流模型直接影响计算的效率和精度.通过大涡模拟(LES)来求解混合流体的湍流方程.宏观守恒方程以及湍流方程参见文献[11—12].
1.1 相间动量交换模型
拖曳力是由相与相之间的速度差引起的,是射流破碎形成的主要诱因.拖曳力Fd,i的模型定义为

式中:αi、αj分别代表燃油相和空气相的体积分数;ρj表示空气相的密度;ui- uj为相间速度差;di表示离散相直径,在喷孔内为空化气泡直径,在喷孔外为喷雾场内油滴的直径;Re为雷诺数;υj为空气相的运动黏度;Cd,i为阻力系数,该项的确定对数值结果的准确性至关重要[13],此处采用 Schiller和 Naumann计算模型,其阻力系数是雷诺数的函数.
表面张力Fs,i是控制两相界面特性的关键因素.对孔内空化及后续的一次破碎都有着重要影响[14],其定义为

式中:σij为相i和j之间的表面张力系数;κ为局部界面曲率,

1.2 准-VOF模型
研究高喷射压力下的射流破碎细节需要获取清晰准确的气-液两相界面.传统 VOF模型[15-16]假设气-液两相的速度和压力在同一网格内一致,只求解单动量方程,弱化了相界面处气-液两相速度差引起的阻力,与实际喷雾过程仍存在一定的差异.与传统VOF界面重构的方法不同,笔者采用的准-VOF模型基于Weller的界面压缩方法[17].
对各相所满足的连续性方程即式(6)中的对流项进行分解,如式(7)所示.


式中:ρi和 αi分别表示第 i相密度和体积分数;ui为第 i相的瞬时速度;M˙则为相间质量传递的质量源项;式(7)右边第二项即为“人工”压缩项,αiαj保证该人工压缩项只在相界面起作用,扩散的自由界面被压缩之后变薄,相界面得以锐化;Cα定义为界面压缩因子,Cα设置为0时,多流体模型将不会对扩散面进行界面压缩,设置为 1时对扩散面施加类似于 VOF样式的界面捕捉,为获取合适的结果,此处将其设置为0.5;定义为相平均速度的模,用于控制压缩速度ui- uj的大小;n为界面单元法向矢量,用于给定压缩速度的方向.
1.3 修正的空化子模型
喷孔内部空化现象是液体燃油压力下降,固-液界面气泡的生成、长大以及溃灭的过程.以往的研究中,气泡数密度通常依赖经验被设置为定值,但实际气泡数密度难以维持为一个定值,其与质量流量、接触角 θ、尤其是饱和蒸气压和局部压力的差值有关.基于异质成核理论对改进的 Schnerr-Sauer的空化模型中的定值气泡数密度J进行修正[14],即

式中:N0为单位体积分子数;B为玻尔兹曼常数;T为成核温度;σ为表面张力系数;hp为 Prancle常数;pv为饱和蒸气压;ψ为单位体积液相中可用于异质成核的表面积;ω为形成临界核所需的最小功的几何校正因子.
采用速度梯度的第二不变量 Q来表征湍流涡结构的瞬时形态,定义为

式中:Ω 为非均匀部分,= [ tr(ΩΩt)]1/2;S为速度梯度张量中均匀的部分,= [ t r(SSt)]1/2.
此外,时间平均的解析动能Ek计算式为

1.4 计算域及边界条件
采用某船用柴油机喷嘴作为研究对象,根据工程图纸建立几何模型并划分结构化网格.为节约计算成本,将计算域分为两种,第一种只有喷嘴主体,该部分结构化网格总数为170万,应用此计算域开展喷雾流量计算及模型验证工作;第二种计算域在第一种计算域的基础之上耦合了喷雾场,充分考虑喷孔内流对射流破碎的影响.图1所示喷雾场结构化网格数为500万,两种计算域最小网格尺寸均为 2µm.几何模型左右两端分别对应压力进/出口边界,其他边界条件均设置为壁面.其中,速度边界条件均设置为无滑移边界,压力边界条件均设置为零梯度边界.

图1 喷嘴几何模型和网格Fig.1 Geometric model and grid of the nozzle
工质采用轻质燃料0号柴油,柴油是复杂烃类混合物,为了简化计算,默认柴油为单一组分并假设其饱和蒸气压为常数 2kPa[15].详细的物性以及模拟工况参数如表1所示.

表1 物性和计算条件Tab.1 Properties and calculation conditions
1.5 数值方法
柴油机喷嘴内流和喷雾近场破碎属于瞬态且紊乱度极高的流动.基于此采用 PISO算法和 SIMPLE算法相结合的 PIMPLE算法来求解多流体模型方程组,以解决压力-速度耦合的问题.根据一阶隐式欧拉方案进行时间项的离散,二阶高斯线性方案用于求解拉普拉斯项和梯度项.对流项的离散则采用 Gauss Van Leer方案,数值积分的时间步长取决于库朗数,库朗数设置为2,初始时间步长设置为0.05μs.
2 模型有效性验证
2.1 喷嘴内流验证及网格无关性验证
图2所示在喷射压力为 60MPa、环境压力为0.1MPa工况下进行网格无关性验证.当喷嘴主体网格数达到17×105时质量流量受网格数的影响已经很小,为节省计算资源采用喷嘴主体网格数 17×105,即第一种计算域进行模型验证工作.VOF模型耦合内流与喷雾场之后,高压力入口边界将导致空气速度急剧升高,从而形成激波致使数值结果发散.由此,只针对喷嘴内流进行模型验证,喷油脉宽为2ms时,两模型的燃油质量和流量系数与笔者已有试验值对比,验证结果分别如图3所示.较传统的 VOF模型而言,多流体-准VOF模型的数值结果和试验值更接近,存在的误差可能是由于柴油单组分假设及喷嘴内表面粗糙度等因素共同造成的.

图2 网格无关性验证Fig.2 Validation of grid independence
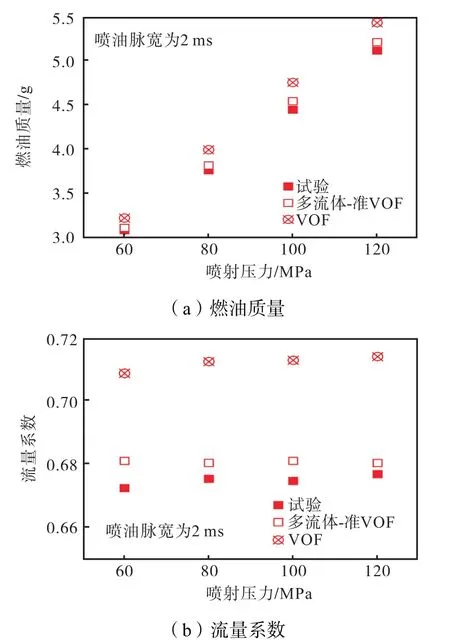
图3 模型验证Fig.3 Validation of model
2.2 大涡模拟的有效性验证
与将流场内所有涡进行统计平均的湍流模型不同,大涡模拟通过滤波函数将湍流分为大尺度涡和小尺度涡,对大尺度涡进行直接解析计算,对小尺度涡进行模化.文献[18]指出当时间平均的解析动能占时间平均总动能的比值达到 80%以上时,即可以认为大涡模拟是有效的,时间平均解析动能的计算式见式(15).在整体流域内,解析动能所占比值在 80%以上,可认为在当前的网格下大涡模拟是有效的.
2.3 射流破碎验证
在高压喷射条件下,喷嘴入口区域可能会出现静压低于饱和蒸气压的负压区,进而发生空化现象.空化模型已在文献[11]当中得到过验证,采用第二种计算域对射流破碎进行验证,结果如图4所示,可以看出数值模拟得到的二维燃油体积分数和可视化试验结果保持高度的一致性,因而认为模型是有效的.

图4 射流破碎验证Fig.4 Validation of jet breakup
3 结果讨论与分析
3.1 喷嘴内流和射流破碎特性分析
图5给出在喷射压力为 120MPa、环境压力为6MPa工况下启喷后41µs时刻的燃油体积分数二维截面分布.计算流域明显分为喷嘴内部空化区、由拖曳力主导的伞状头部破碎区及由空化、湍流和拖曳力三者共同主导的主喷雾区.这与 Wei等[19]在可视化喷嘴内观察到的喷嘴内流和近场破碎结构一致.

图5 空化区和射流破碎区Fig.5 Cavitation area and jet breakup area
结合图6所示不同喷射压力下的喷孔内燃油流动过程和图7所示沿轴线的速度和压力的分布曲线可知,当液体燃油流经喷孔入口时流通面积急剧减小,速度急剧升高.高燃油流速将导致流体在喷孔入口的突变截面处发生分离,形成缩脉,进而形成较低的流场静压,当该静压低于饱和蒸气压时即发生空化现象.由图6可知,在启喷后 34µs时 3种喷射压力下的燃油均流动到出口.在相同的环境压力下,喷射压力越高,燃油的流速越快,燃油流动到喷嘴出口所用时间越短.随着流动的持续发展,液体燃油沿程所受到的阻力变大,但并不影响速度的增加,这与Payri等[3]观察到的现象是一致的.

图6 不同喷射压力下喷孔内液体燃油体积分数发展对比Fig.6 Comparison of the development of liquid fuel volume fraction in nozzle orifice under different injection pressures

图7 喷孔轴线上的压力和相平均速度分布Fig.7 Axial pressures and average velocity distribution at the orifice center line
3种不同喷射压力下的空化覆盖区域向喷孔出口持续延伸,最终均发展为超空化.燃油的流通面积在空化发展稳定后也逐渐趋于稳定,质量流量不再发生变化.图8给出射流贯穿距为3.41mm时3种不同喷射压力下喷孔出口径向蒸气体积分数分布对比.3种喷射压力在与射流贯穿距下的蒸气体积分数发展十分接近,即该船用喷嘴喷孔内部达到超空化之后,其对于初次破碎的影响在 3种不同压力梯度下是趋于一致的.

图8 不同喷射压力下喷孔出口径向蒸气体积分数分布Fig.8 Distribution of radial vapor volume fraction at the outlet of different injection pressures
喷嘴内部的湍流扰动随着燃油流速的持续升高以及空化的发生而获得必要的生长条件.同时,高速燃油和喷雾场内静止空气相互碰撞,极大的速度梯度导致喷孔出口气-液界面存在很强的相互剪切作用进而产生较强的拖曳阻力,如图9c所示.
在主喷雾区,拖曳力促进图5中射流表面波的初始生成以及后续的快速发展,直至最终表面波失稳并剥离出轴向液带.图9a速度矢量所示在伞状头部破碎区,液体燃油抵达喷孔出口后由于流通面积急剧扩大而摆脱束缚,获取径向速度.射流尖端迎风受阻,在径向速度和拖曳阻力的双重作用下与空气发生动量交换后发生径向扩散,表现为伞状结构.此外,图9b所示的伞状结构内部强轴对称涡的形成,对伞状尾缘的破碎起到了积极的影响.

图9 轴对称涡及气-液界面相对速度引起的拖曳力Fig.9 Axisymmetric vortex and drag force caused by the relative velocity at the gas-liquid interface
在数值研究中,湍流涡结构的大小和位置的可视化是十分重要的,而通过处理速度梯度的第二不变量Q的等值面则可以很好地呈现出瞬时的湍流涡旋形态,其具体定义见式(14).
图10给出喷射压力为 120MPa、环境压力为6MPa时的湍流涡结构 Q值的三维等值面.喷孔出

图10 Q=2×1011s-2的等值面Fig.10 Iso-surface of Q=2×1011s-2
图11为启喷后 35~40µs不同时刻伞状射流头部的三维破碎过程.从绿色箭头的指向可以看出,液环在径向速度分量、气动力以及周向表面张力的共同的作用下收缩变细直至在直径最小点发生掐断破碎,从而形成尺寸各异的环形液带的过程.红色箭头指向则清晰地呈现了液带破碎成大液滴的过程,该破碎机理与液环破碎断裂成液带的机理完全一致.剥离出的液带和液滴在其内部的轴对称涡和气动力的作用下被卷至伞状头部的后端,大尺寸的液带液滴受到更大的空气阻力而被后续的小液带液滴追赶碰撞.同时,尺寸各异的液带和液滴与主喷雾区的射流也可能发生相互碰撞,从而促进雾化.口处存在大量的湍流涡结构.在主喷雾区,湍流涡结构主要以轴向形式存在,液带沿着流向被剥离.在伞状头破碎区,湍流涡为环状结构,结合图9c可以看出,大量的湍流环形涡使射流颈部掩藏于背风面而免受气动力的侵扰,径向扩张的伞状头部承受了大部分的轴向阻力作用,这是射流头部形成环形液带的主要原因.

图11 液带的破碎和大液滴的形成Fig.11 Fracture of ligaments and formation of large droplets
3.2 喷射压力对初次破碎的影响机理
图12给出了不同喷射压力下定环境压力为6MPa及启喷后41µs时刻的液体燃油体积分数等值面,其中颜色代表燃油速度大小.可以看出低喷射压力下射流中心速度较低,表面波的波幅和波长处在发展初期且普遍偏小,射流头部尾缘存在少量的液带.随着喷射压力的升高,燃油流速和贯穿距在短时间内迅速增大,在更强烈的扰动下射流表面波与环境气体之间的卷吸作用加剧,发展显著.液柱直径变小破碎也更为剧烈.与此同时,射流流速的增加使液体射流和空气间的剪切作用变强,射流头部受到更大的拖曳力作用,如图13所示.在速度径向分量的作用下,射流头部逐渐发展成为中部更宽的伞状结构,大量的小直径液带液滴被剥离并向射流后部转移.由此可推断,在高喷射压力下,射流头部的迎风面积变大,承受的拖曳阻力变强,伞状头部剥离出的环形液带相对低喷射压力情况更密集、尺寸更小,雾化效果更优.射流的轴向贯穿能力随着射流的推进会慢慢减弱,但剧烈的初次破碎效应对后续的二次破碎以及整体雾化质量的提高是毋庸置疑的.

图12 不同喷射压力下液体燃油体积分数为0.5的等值面Fig.12 Liquid fuel volume iso-surface(α=0.5) at different injection pressures

图13 不同喷射压力下气-液界面的拖曳力Fig.13 Contour of drag force at the gas-liquid interface at different injection pressures
图14为不同喷射压力下表征湍流涡结构 Q的等值面对比,其中颜色代表速度大小.从内部流动的涡结构可以看出,随着喷射压力的增加,喷孔内部边界层均匀分布的涡结构相差不大,空化效应对射流破碎的影响在不同的压力梯度下趋于一致,这与图8呈现出的结果相匹配.在主喷雾区,高喷射压力下喷孔出口具有更强的湍流涡结构,高速度梯度将大幅提升气-液间的相互作用,因而产生了更强的轴向涡流以及直径更小的射流.在伞状头部破碎区,喷射压力为80MPa时射流颈部的轴对称环形涡开始出现裂痕,随着喷射压力的增加,在气动力作用下逐渐发展成卷曲的涡结构,但仍保持对称特性,在射流贯穿的过程中该湍流涡结构最终将打破轴对称特性,发展成为相对于主喷雾区轴向涡而言,尺度更大但结构相似的涡结构,从而促进射流颈部的破碎.从图14中的右视图可以看出,高喷射压力下的射流头部被更密集的环形涡结构包裹,伞状头部尾缘已经形成大量的液滴.因此,提高喷射压力将提升气-液间相互作用以及喷孔出口处的湍流涡结构,使射流表面和射流头部分别形成相对低喷射压力情况更多、更强的轴向涡和环形涡,从而促进雾化.

图14 不同喷射压力下的湍流涡结构Q=1012s-2 等值面Fig.14 Turbulent vortex structure represented by the isosurface Q=1012 s-2 at different injection pressures
4 结 论
基于 OpenFOAM 平台,采用多流体-准 VOF模型对某船用低速机喷嘴的内流和近场进行了耦合数值研究,充分考虑了内部空化、出口湍流和气动力对初次破碎的影响,并将该模型的计算结果与传统的VOF模型进行对比,得出以下结论:
(1) 在同等计算条件下,多流体-准 VOF与传统的 VOF模型相比,具有更高的计算精度;前者在准确预测出伞状射流头部的同时,清晰呈现了液柱表面波的生成和发展以及液带和液滴剥离的完整过程.
(2) 在给定的3种压力梯度下,喷孔内部均发生超空化,边界层内湍流涡结构的分布均匀且相差不大,空化效应对射流破碎的影响将不再随喷射压力的升高而发生变化.
(3) 在主喷雾区,高喷射压力下喷孔出口具有更强的湍流涡结构,并且高速度梯度将大幅提升气-液间的相互作用,由此产生了更强的轴向涡流以及直径更小的射流;在伞状头部破碎区,提高喷射压力将导致气-液相间速度差变大,射流头部的迎风面积变大,承受的拖曳阻力变强,伞状头部剥离出更密集、尺寸更小的环形液带以及液滴.
(4) 定环境压力,提高喷射压力将促进伞形射流尖端以及液柱的破碎,为后续的二次破碎提供更好的初始条件.

