低负荷工况下天然气发动机燃烧不稳定性分析

刘津津，丁顺良，高建设，宋恩哲，杨福源

(1.郑州大学 机械与动力工程学院，河南 郑州 450001；2.哈尔滨工程大学 动力与能源工程学院，黑龙江 哈尔滨150001；3.清华大学 汽车安全与节能国家重点实验室，北京 100084；4.清华大学 车辆与运载学院，北京 100084)

随着经济的快速发展，环境污染问题日益突出，节能减排已成为发动机行业的重要任务[1].与汽油发动机、柴油发动机相比，天然气发动机以其燃料清洁、热效率高、经济性能高、安全性能好以及燃料储量丰富等特点逐渐成为替代燃料发动机的首选[2].在稀燃工况下，天然气发动机经济性、热效率和排放性能显著改善，但燃烧过程会出现循环变动现象，从而影响发动机的稳定性[3]，特别是在稀燃边界附近循环变动明显增大，燃烧稳定性恶化，严重影响发动机性能.研究[4]表明，天然气发动机燃烧不稳定性如果能被较好地控制甚至消除，其动力性可提高10%.

天然气发动机是一个多输入、多输出和强耦合的复杂非线性系统，其燃烧过程受诸多因素的影响，导致发动机控制难度增加，燃烧不稳定的动力学特性不仅表现出准周期特性，还出现明显的混沌特征[5-11].而非线性动力学是分析非线性系统运动状态随时间变化的一门学科，混沌是当系统的非线性程度达到足够高时出现的一种状态，是指系统长期行为对初始条件的变化异常敏感，并且无法精确重复的现象，是非线性程度达到足够高时，系统普遍具有的一种复杂动力学行为[5].非线性动力学和混沌理论为复杂动力学系统的分析提供了有效方法，为研究天然气发动机燃烧不稳定的内在特性及演化过程提供了可能，国内外学者对此开展了相关研究.Litak等[6-7]利用重现量化分析和小波变换等方法，对多点喷射天然气发动机在 4种当量比下的指示平均有效压力(IMEP)进行分析，发现随着混合气浓度变稀，燃烧动力学特性呈现出由随机性向确定性的过渡，前后循环的强烈交互作用导致系统出现高频间歇现象.Sen等[8-9]针对天然气直喷火花点火发动机，通过对时间序列的小波分析，结合常规统计和多重分形分析，对 IMEP、火焰发展时间、主燃烧时间和总燃烧时间的时间序列进行研究发现，表征燃烧不稳定性的时间序列，其动力学特性有很强的关联性.姚宝峰等[10]以一台点燃式增压电喷天然气发动机为研究对象进行了多组试验，对天然气发动机的峰值压力、最大压力升高率及其位置、IMEP进行了循环变动和相关性分析发现，IMEP和峰值压力存在较为稳定的线性关系，在燃烧稳定且完全的情况下峰值压力可以较为准确地反映天然气发动机的燃烧不稳定性，但在燃烧恶劣的条件下峰值压力对燃烧不稳定性的分辨力较低.Yang等[11]利用相空间重构、最大李雅普诺夫指数和吸引子的关联维等方法对增压中冷天然气发动机燃烧过程的不稳定性进行了研究发现，燃烧过程的相空间吸引子在有限范围内呈现出交叉、折叠和相互扭曲的复杂几何结构，最大李雅普诺夫指数均大于 0，关联维均能达到饱和并呈现分数维，说明燃烧系统呈现出明显的混沌特性；在稀燃极限时，火花塞附近混合气浓度分布的微小变动都会对发动机的稳定性造成很大影响，燃烧稳定性对初始条件变化特别敏感.

国内外学者针对发动机燃烧不稳定性进行了大量研究，但还存在一些有待解决的问题.目前，天然气发动机燃烧不稳定性的研究大多针对某一全局参数(如 IMEP)进行循环变动分析，不能全面显示出发动机整个燃烧过程的不稳定状态，从而无法对影响燃烧稳定性的关键因素做出具体分析；涉及非线性动力学分析时，也多集中于 IMEP的返回映射分析，虽能体现循环与循环间的关联关系，但无法反映单个燃烧循环内部的演变规律，无法揭示循环内部的动力学演化机理进而对天然气发动机进行有效控制.基于此，笔者对天然气发动机单个工作循环中每个曲轴转角下的缸压均进行循环变动分析，研究发动机燃烧过程各个阶段的不稳定性，同时分析缸压时间序列的相空间重构，以揭示燃烧循环内部的动力学演变规律，并结合 IMEP、燃烧中点(CA 50)的返回映射和燃烧始点(CA 5)、燃烧终点(CA 90)的分布图，研究燃烧循环与循环之间强-弱关系和随机性与确定性共存的混沌特性.由于低负荷下天然气发动机的燃烧不稳定性更加明显，针对低负荷工况，以过量空气系数为关键影响因素，对天然气发动机燃烧不稳定性进行研究.

1 试验设备及方案

研究对象是一台电控多点顺序喷射天然气发动机，发动机的主要参数如表1所示.

表1 天然气发动机的主要参数Tab.1 Main parameters for the natural gas engine

首先在过量空气系数φa=1.0、发动机转矩为50N·m 时记录燃料量，保持该燃料量不变，通过改变节气门的开度来改变φa的方式，利用宽域氧传感器对φa进行实时监测.缸内压力时间序列由燃烧分析仪、缸内压力传感器、编码器和计算机等组成的数据采集系统获取，该系统的最高采集分辨率可达 0.025°CA，图1为试验台示意.天然气发动机在低负荷下燃烧不稳定性更为明显，为了探索发动机在稀燃边界的稳定性变化，选取了可在较大φa范围内进行试验数据采集的转速.故在 1000r/min、25%负荷及φa分别为 1.0、1.2、1.4、1.6、1.8和 1.9不同工况下进行台架试验.针对上述6种工况下分别测取1800个工作循环的缸内压力时间序列，其中数据采样间隔为1° CA，每个循环包括720个数据点.

图1 试验台示意Fig.1 Schematic of the experimental bench

图2和图3分别为1000r/min、25%负荷及φa为1.0、1.6和 1.9工况下试验测得的缸内压力时间序列和IMEP时间序列.燃烧过程中缸内压力存在明显波动，φa=1.9时，燃烧稳定性恶化.

图2 缸内压力时间序列Fig.2 In-cylinder pressure time series

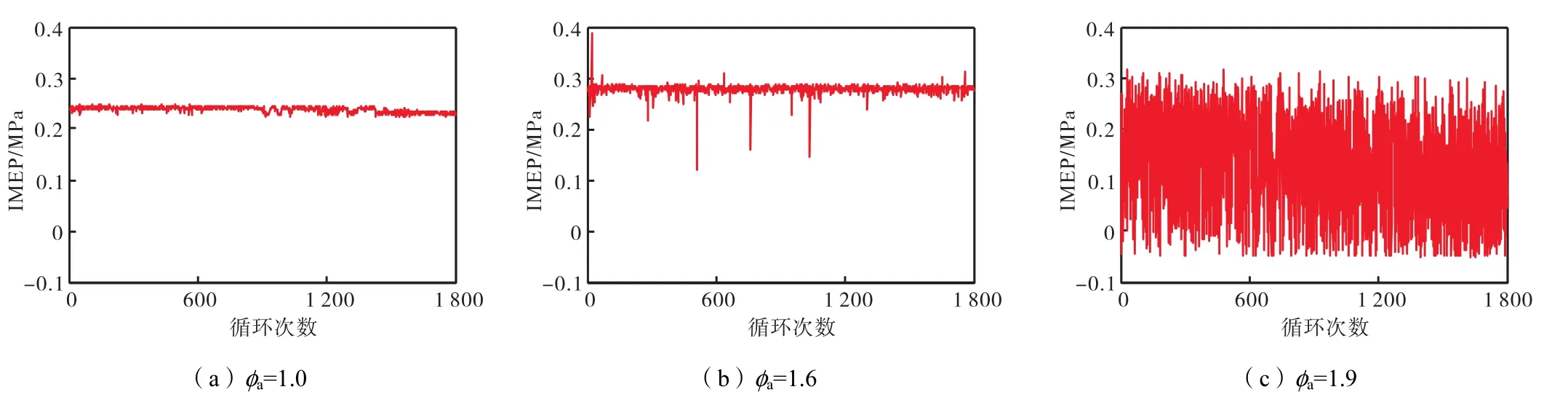
图3 IMEP时间序列Fig.3 IMEP time series

2 燃烧特征参数的循环变动分析

天然气发动机燃烧不稳定性会导致燃烧特征参数的循环变动(CCV)，CCV是反映发动机燃烧不稳定性的一个重要指标[12-13].CCV计算公式为

2.1 缸压循环变动分析

为分析缸内压力在各曲轴转角处的循环变动情况，对 1800个工作循环的缸内压力进行循环变动分析.图4为不同φa工况下天然气发动机的缸压曲线和各曲轴转角处缸内压力CCV曲线.CCV曲线有两个明显峰值，前一个是进气阶段引起的变动，后一个是燃烧阶段引起的变动.图5为进气阶段和燃烧阶段引起的 CCV峰值.进气阶段 CCV峰值随着φa的增大而下降，燃烧阶段 CCV峰值随着φa的增大而上升.在进气阶段，进气门的开关会引起缸内气流扰动，而使CCV增大；φa=1.0时，所需空气量较少，节气门开度较小，微小的外界进气扰动就会使缸内压力变化较大，且缸压平均值很小，当缸压出现微小变动时，会导致CCV变化较大.随着φa增大，所需空气量增多，节气门开度变大，抗干扰能力增强，外界扰动引起的缸内压力 CCV峰值降低.在燃烧阶段，上止点前混合气体被点燃，由燃烧导致CCV的增大，φa=1.0时，不发生稀燃，燃烧速度快，燃烧过程的缸压平均值较大，当缸压出现较大变动时，CCV值的变化仍不如进气过程明显，CCV峰值相位提前于缸内压力峰值相位；随着φa的增大，燃烧不稳定增强，CCV 的峰值逐渐上升，峰值相位滞后；φa过大时，CCV 峰值明显上升，峰值相位滞后于缸内峰值压力相位，这说明滞燃期过长，后燃现象严重.

图5 进气和燃烧阶段缸压时间序列的CCV峰值Fig.5 Peak CCVs of in-cylinder pressure time seriesat air intake and combustion stages

采用自然吸气的天然气发动机，进气过程中缸内压力比燃烧时的缸内压力小得多.从公式(1)可知，分母较小时，分子的微小变化将会引起 CCV较大变化，这也是循环变动系数分析的一个缺陷所在，即不能全面体现燃烧不稳定的程度.因而会出现图4a所示的φa=1.0时，进气过程中的 CCV值变化很大，而燃烧过程 CCV值的变化不如进气过程明显.因此，采用了相空间重构、返回映射等非线性分析方法对燃烧不稳定性进行进一步研究.

图4 缸内压力时间序列在各曲轴转角处的CCV曲线Fig.4 CCV of in-cylinder pressure time series at each crank angle

2.2 CA5和CA90的循环变动分析

图6为 1000r/min、25%负荷工况下的燃烧始点、终点相位分布.随着φa的增大，CA 5和CA 90均呈滞后趋势，且波动范围逐渐扩大，φa为 1.8、1.9时CA 5和CA 90的分界线逐渐消失.图7为不同φa工况下CA 5和CA 90的CCV曲线.随着φa增大，CA 5和CA 90的CCV均增大，这主要是因为混合气浓度变稀会导致燃烧速度降低，滞燃期增长，点火可靠性降低.图8为不同φa工况下CA 5和CA 90的统计分析.CA 5及其标准差均呈上升趋势，CA 90相位及标准差在φa为 1.2～1.8呈上升趋势，当φa=1.0时CA 90的标准差较大，当φa=1.9时CA 90的平均相位稍有降低.

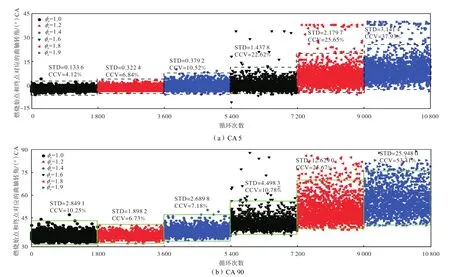
图6 不同φa工况下的CA 5和CA 90分布Fig.6 Distributions of CA 5 and CA 90 under different φa conditions

图7 不同φa工况下CA 5和CA 90的CCV分析Fig.7 CCV analyses of CA 5 and CA 90 under different φa conditions

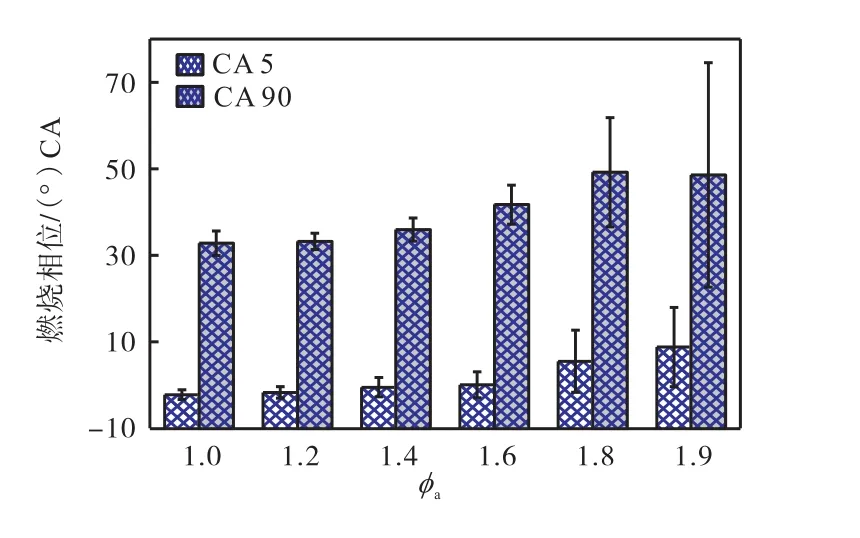
图8 不同φa工况下CA 5和CA 90的统计分析Fig.8 Statistical analyses of CA 5 and CA 90 under different φa conditions

φa=1.0时，由于空气量较少，会导致燃烧不完全现象，CA 90分布范围较大，CCV较高；随着φa的增大，空气量逐渐增加，燃烧速度降低，滞燃期逐渐变长，CA 90的范围相对集中.φa大于1.4时，空气量较多，混合气浓度变稀，燃烧速度变慢，CA5和 CA90滞后且波动范围变大，CCV明显上升，后燃现象越来越严重.φa=1.9时，空气量过多，出现失火现象，因而CA90的平均相位有所提前.

3 相空间重构分析

相空间是指包含了系统所有可能状态，且每个可能状态都可以用一个相点来表示的抽象空间.对系统相空间进行数学公式描述，系统某时刻的状态可以通过相空间的某个相点来体现，系统随时间发展演变的规律由相空间中的相点运动轨迹来描述，轨线构成了系统的相空间吸引子.相空间可以通过抽象出系统所有的实质性信息来反映其内在规律[14].非线性系统中任一分量的演化和发展都是由与之相互作用着的其他分量所决定，任一分量的演化进程中也隐藏了相关分量的信息.因此，在相空间中将有规律的吸引子恢复出来，以此来找到各相关量的关系[15].天然气发动机燃烧过程动力学特性的数学机理复杂，并没有确切的数学公式描述，但所有影响燃烧过程的变量，都能够在试验观测到的燃烧过程缸压时间序列重构的相空间中找到痕迹.

发动机燃烧过程是一个多变量耦合作用的非线性系统，在嵌入维数合适的相空间中可以更直观地展示出各分量之间的隐藏信息[16].相空间重构常用的方法有时间延迟坐标法和导数法，其中导数法虽然运算较为简单，但对噪声敏感，容易产生较大误差.故选择延迟坐标法对缸内压力时间序列进行相空间重构，通过吸引子在相空间的轨线运动规律对燃烧过程的运动特性进行分析.延迟坐标法的定义为

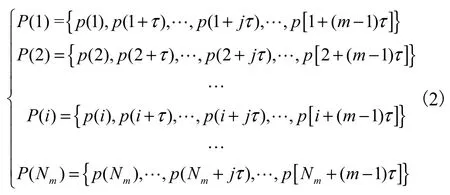
式中：τ为延时坐标；m为嵌入维数；p(i)为缸内压力时间序列中的数据点； P (Nm)为{p(Nm),…,p(Nm+jτ),… ,p[Nm+(m-1)τ] }向量；Nm为总行数，Nm=N-(m-1)τ.由式(2)可知，利用坐标延迟法进行相空间重构，嵌入维数 m和延迟时间 τ是两个必不可少的参数.

采用自相关函数法计算延迟时间，选取自相关函数首次降到 C(0)/e时的 τ值为最优延时坐标，此时吸引子轨线的运动规律较为清晰，自相关函数为

采用虚假近邻法(FNN)计算最小嵌入维数 m，FNN分数随着m的增加而下降，选择FNN分数下降到10%的m值作为最小嵌入维数.FNN公式为

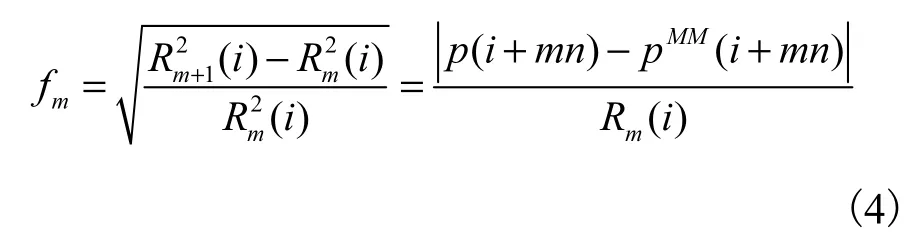
式中：pMM(i)为 p(i)的最近邻点，MM 为上标，表示最近邻点；Rm(i)为 pMM(i)和 p(i)在相空间中的距离；n=τ/t，t为采样间隔.

图9为不同φa工况下吸引子的演化规律及对应的最优延时坐标和最小嵌入维数.在相空间中吸引子的轨线呈现非周期、折叠、扭曲、相互缠绕和交叉的复杂几何结构，但是轨线只在限定的范围内反复出现，表现出有序的特点，闭合的吸引子轨线演化途径反映了天然气发动机的整个燃烧过程的状态.

图9 吸引子结构随φa的演化规律Fig.9 Evolution patterns of the attractor structure with φa

φa较小时，吸引子轨线较为紧凑，运动范围较小，因点火而产生的轨线分离程度较低，由燃烧引起的 Y轴最大值的波动较小，燃烧后期的轨线分离程度较低，轨线经过 X轴最大值又趋于重合后波动仍然较低，证明发动机燃烧不稳定性较低，燃烧过程整体呈现准周期特征；随着φa的不断增大，吸引子的轨线逐渐变得疏散，吸引子的运动范围增大，轨线分离程度增强，一部分轨线点火后的发展速度缓慢，甚至不经过轨线分离处就开始降低，由燃烧引起的 Y轴最大值波动变大，燃烧后期的轨线波动增大，轨线经过 X轴最大值又趋于重合后波动范围变大，由此表明发动机燃烧的不稳定性增强.

当φa=1.0时，由于燃烧速度较快，保证了燃烧过程的轨线波动较小，分散程度较小，吸引子较密集，同时由于空气量较少，虽然燃烧的可靠性高，但会存在部分燃料不能完全燃烧的现象，经济性较低.随着φa的增加，空气量增多，燃料完全燃烧，峰值压力有所上升，吸引子增大，但混合气浓度降低会延长燃烧持续期，导致一定程度上的燃烧不稳定，因而吸引子变得疏散.当φa过大时，过稀的混合气使燃烧可靠性降低，会导致失火现象，此时的吸引子结构较为复杂，活塞往复运动引起的流场变化对系统动力学的影响在加强，而燃烧过程对缸内动力学的作用在减弱.

4 返回映射分析

返回映射是相空间重构在 m=2、τ=1时的特例，通过映射点的分布规律，对系统的随机性和确定性共存的混沌特性进行分析.对于随机性较强的时间序列，返回映射图呈现一种随机均匀分布在一定直径的圆形区域内的结构，对于确定性较强的时间序列，返回映射图呈现一种完全不同于随机分布的结构.返回映射的表达式为

式中：X、Y分别为二维平面的横、纵坐标点集.

4.1 IMEP的返回映射分析

IMEP可以综合表征整个燃烧循环的缸内压力情况，针对 IMEP的返回映射可以反映出燃烧前、后循环之间的内在关系.图10为1000r/min、25%负荷工况下天然气发动机IMEP的返回映射，可以看出映射点沿对角线大致对称分布.当φa=1.0时，混合气浓度较大，映射点在蓝色圆形区域中呈随机分布，天然气发动机燃烧前、后循环之间的关联性较弱，随机性占主导地位；φa为1.2和1.4时，混合气浓度变稀，有映射点开始逐渐逃离蓝色区域；φa=1.6时，蓝色圆形区域内映射点的分布不再呈现云状随机分布，而是开始出现一部分映射点向 X轴减小的方向发展，另一部分映射点向 Y轴减小的方向发展，形成上三角形区域，并且越来越多的映射点逃离蓝色区域；φa=1.8时，更多的映射点从圆形区域向两坐标轴减小的方向发展，形成显著的上三角形区域，远离圆形区域的点增多，这表明燃烧过程前、后循环之间的关联性加强，“强-弱”交替的燃烧循环具有一定的混沌特性；当φa=1.9时，混合气浓度过稀，蓝色区域消失，映射点呈正方形结构沿对角线对称分布，分布更加混乱，燃烧过程前、后循环的关联性更强，混沌特性也更明显.造成这种现象的主要原因是随着φa增大，混合气浓度变稀，燃烧速度变慢，燃烧可靠性降低，出现不完全燃烧甚至失火现象，前一循环的残余废气、当前循环的进气和混合气分布的微小变动都会对当前循环产生很大的影响，导致前、后循环的关联性很强.

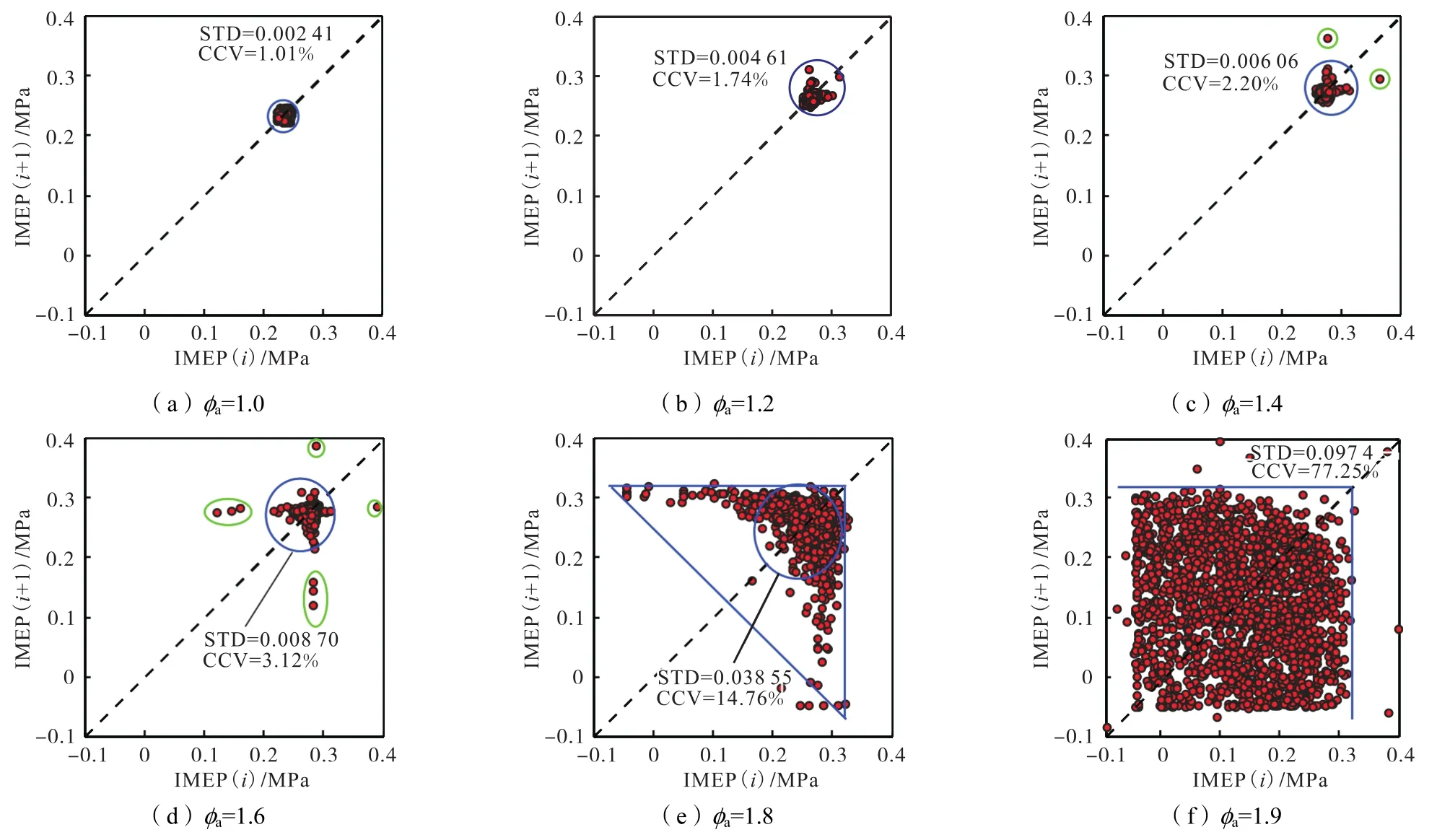
图10 IMEP的返回映射随φa的演化规律Fig.10 Evolution patterns of return map of IMEP with φa

图11为不同φa工况下IMEP的统计分析结果及发动机功率的变化.当φa从 1.0增大到 1.6时，空气量增多，燃烧更充分，IMEP的平均值增大，发动机做功能力增强，但同时 IMEP标准差和 CCV也增大，燃烧不稳定性增强；当φa为 1.8～1.9时，混合气浓度过稀，IMEP的平均值降低且标准差变大，是因为出现了失火现象，发动机燃烧稳定性和做功能力都受到严重的影响.

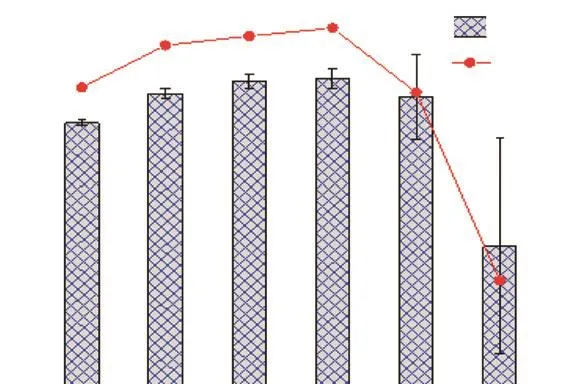
图11 不同φa工况下的IMEP统计分析及发动机功率变化Fig.11 Analysis of IMEP and engine power under different φa conditions

4.2 CA 50的返回映射和CCV的相关性分析

CA 50是反映发动机燃烧效率和排放性能的重要参数，通过CA 50的返回映射，能更清楚地研究燃烧过程的动力学特性.图12为CA 50返回映射点随φa的演化规律，CA 50映射点沿对角线大致呈对称分布.当φa=1.0时，CCV 为 16.66%，有少量映射点逃离蓝色区域(图中由绿色椭圆标出)，这是因为此时缸内空气量较少，导致燃烧不完全；φa=1.2时，CCV为18.81%，映射点随机分布在圆形区域中，此时空气量充足，燃烧速度较快，滞燃期短，燃烧较为完全；φa=1.4时，CCV为 19.55%，映射点所处的圆形区域变大，这是空气量增多，燃烧速度变慢，CA 50滞后造成的；φa=1.6时，CCV 为 24.22%，虽然大部分映射点还分布在蓝色区域内，但有部分映射点脱离蓝色区域向 X、Y轴增大的方向发展，这说明随着空气量的增多，燃烧速度变得更慢，出现了部分后燃现象；φa=1.8时，CCV为 32.26%，有更多的映射点逃离中心，逐渐形成三角区域，这说明后燃现象越来越明显，前一燃烧过程对后一燃烧过程的影响作用在加强；φa=1.9时，CCV 为 36.62%，映射点与 IMEP映射点的分布相反，呈现下三角形分布，后燃现象严重甚至发生失火现象.

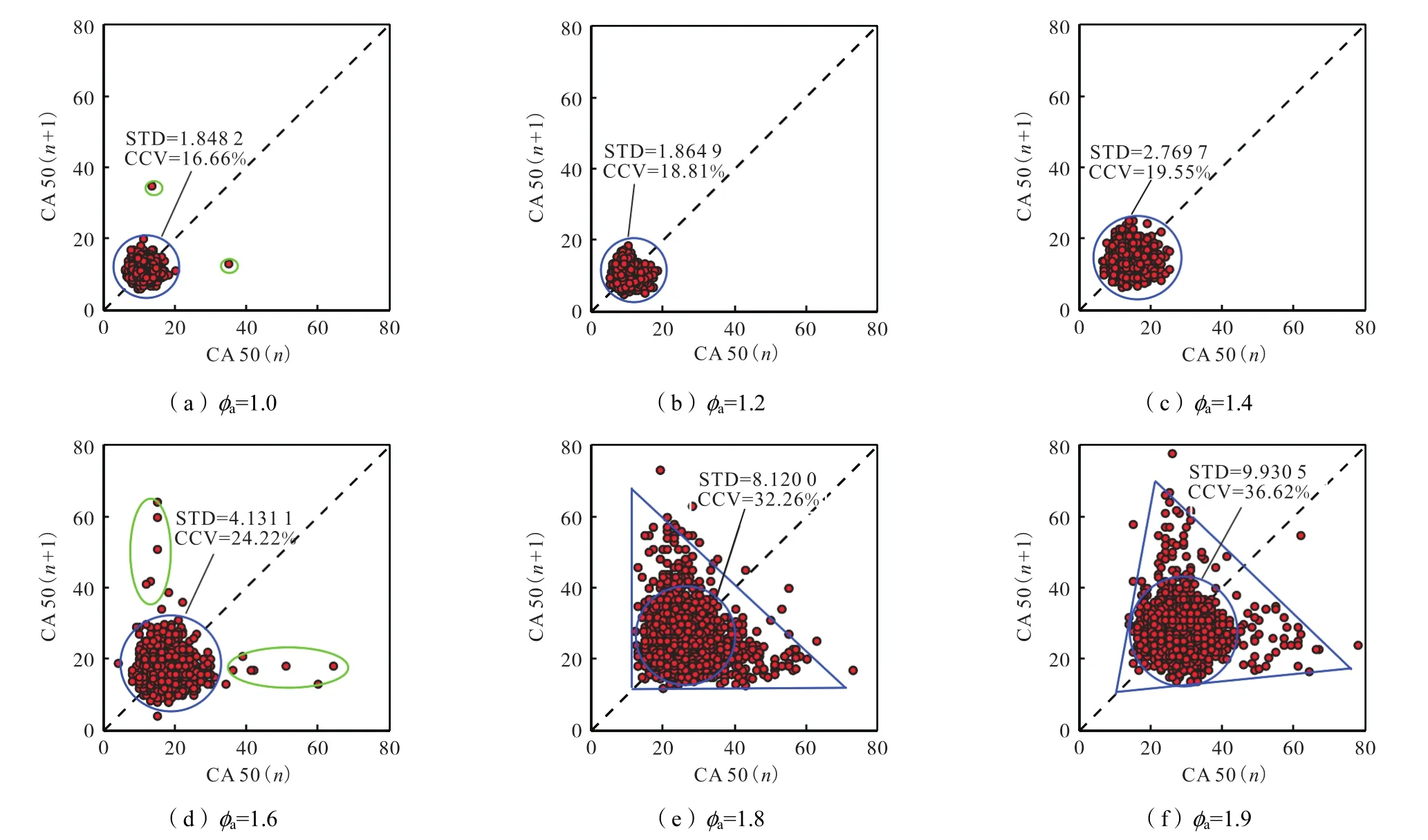
图12 CA 50的返回映射随φa的演化规律Fig.12 Evolution patterns of return map of CA 50 with φa

图13为CA 50随φa变化的统计分析，随着φa增大CA 50整体趋势呈现滞后，但φa=1.0时，CA 50的平均值较φa=1.2偏高，这是因为φa=1.0时空气量较少，部分燃料燃烧不完全使得 CA 50滞后，这与CA 50的返回映射点分布规律一致.

图13 不同φa工况下的CA 50统计分析Fig.13 Statistical analysis of CA 50 under different φa conditions

表2 为 CCVIMEP与 CCVCA5、CCVCA50、CCVCA90和 CCVpmax的相关性系数R.不同 CCV之间存在较强相关性，CCVIMEP反映的是循环之间的整体变动情况，而 CCVCA5、CCVCA50、CCVCA90、CCVpmax分别反映了燃烧始点相位、燃烧中点相位、燃烧终点相位和燃烧过程中的循环变动情况，不同阶段的 CCV分析结合燃烧非线性动力学分析，可以对各个阶段的天然气发动机燃烧不稳定性有更加全面的认识.

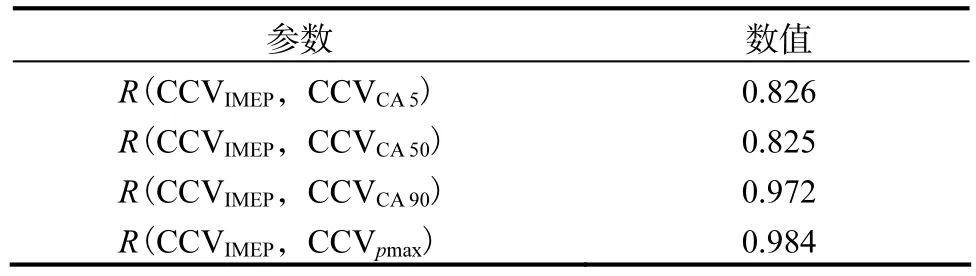
表2 不同CCVs之间的相关系数Tab.2 Correlation coefficients between different CCVs

5 结 论

在低负荷、φa为1.0～1.9工况下进行天然气发动机台架试验，利用循环变动系数、相空间重构和返回映射等方法对缸内压力时间序列、IMEP、CA 5、CA 50和CA 90等燃烧过程参数进行分析，得出以下结论：

(1) 随着φa的增大，进气阶段引起的缸内压力循环变动系数峰值逐渐下降，燃烧阶段引起的缸内压力循环变动系数峰值逐渐上升，且相位滞后，燃烧不稳定性逐渐增强；CA 5、CA 50和CA 90波动范围及对应的循环变动系数均不断增大，滞燃期变长；φa过大时存在后燃和失火现象，发动机稳定性和做功能力大大下降.

(2) 在不同φa工况下，天然气发动机燃烧过程呈现出不同程度的混沌特性，且燃烧不稳定性与混沌特性存在较强的相关性.

(3) 当混合气浓度较大时，天然气发动机燃烧过程相空间中吸引子轨线较紧凑，燃烧前、后循环的关联较弱，随机性占主导作用；随着混合气浓度变稀，相空间中吸引子轨线越来越分散，燃烧过程前、后循环的关联性逐渐加强，随机性和确定性共存，具有一定的混沌特性；混合气浓度过稀时，燃烧前、后循环的关联性更强，关系更复杂，混沌特性更加明显，对初始条件异常敏感.