基于声发射小波熵的混凝土损伤检测技术研究

朱利峰

（中国铁路上海局集团有限公司安全监察室，上海 200081）

引言

混凝土是一种主要的建筑材料，价格低廉，便于成型。然而，材料的非均质性使其力学性能有较大偏差，失效预测非常困难。混凝土断裂过程的复杂性是由于裂缝尖端的微观/宏观裂纹群的存在，也称为断裂过程区（FPZ）。损伤过程中发生多种断裂机制，每种断裂机制在整体损伤中的严重程度不同。断裂机制，如裂缝桥接、分叉、闭合、终止以及偏转、延迟和加速裂缝等，是人们可以用来描述混凝土FPZ 内的裂缝扩展的少数标签。结构健康监测的关键任务是发现如何确定损伤敏感特征，以及如何从传感器测量的数据中提取有关这些特征的信息，以检测结构的损伤或变化。声发射技术（AE）是结构健康监测方法之一，主要进行结构瞬态损伤过程的无损评估。在过去的几十年里，它有了相当大的发展。声发射技术通过安装在材料表面的压电传感器获得的材料裂纹产生的弹性应力波。声发射是动态断裂发展过程留下的痕迹。可将每个声发射事件视为一个裂纹，但也不能排除多个裂纹同时发生的可能性。输入信号的速率及参数，如振幅、能量和频率，通常与裂缝的密度、强度和严重程度相关。对于性能良好的材料，如金属，声发射监测是一种高效准确的裂缝源定位和损伤表征技术。然而，由于水泥基材料(如混凝土)固有的非均质性，在混凝土中尚未达到所需的检测精度。混凝土中裂缝的产生和扩展是由水泥基开裂、骨料开裂、骨料脱粘、钢筋脱粘、断裂面与粘结面摩擦等复杂现象引起的[1]。因此，裂缝模式分类和裂纹源识别是混凝土声发射中除裂纹源定位问题外最受关注的问题。这些问题解决后即可查明破坏原因，从而进行结构健康评估。

基于声发射信号时域参数的研究方法适合于混凝土损伤分析。对于裂纹模式的分类，参数化方法采用上升角(RA-上升时间/幅度)和平均频率(AF-计数/持续时间)两个参数。对钢筋混凝土(钢和纤维)进行裂纹模式分类研究时，常常采用RA-AF 方法。另一种裂纹分类技术称为矩张量分析，采用线性反演法确定矩张量的数学表达式，在时域和频域都使用格林函数表示[2]。然而，对于类似混凝土的非均质材料，确定格林函数是非常繁琐，因此，尽管矩张量分析在理论上是可靠的，但在混凝土裂缝分类方面的应用并不广泛。

与裂纹模式分类不同，裂缝源识别主要集中在频谱分析上，因为每一个基本的材料成分在声发射信号的频域上都有各自的特征。在这方面，利用光谱分析和统计技术在复合材料声发射源识别方面取得了显著的进展。Rossi 等人对混凝土光谱分析的早期研究提出了将傅里叶变换得到的线性光谱的信号能量在某些频段进行划分，并将其各自的比例进行频谱分类，可用于解释断裂机理。Burud 和Chandra Kishen 利用小波变换(WT)得到了频率子带能量比，对普通混凝土和钢筋混凝土的声发射信号进行了比较[3]。Yoon 等人利用WT 研究了腐蚀钢筋混凝土中的声发射信号，并分析了损伤破坏阶段附近的高能信号，该损伤阶段由几个间隔很短的事件组成[4]。Wang 等人也报道了类似的研究结果，即当混凝土受压破坏时，声发射信号从突发型转变为连续型。Sagaidak 和Elizarov 得出的结论是，裂纹扩展降低了混凝土弯曲声发射光谱中的主导频率[5]。Wang 等人利用峰值频率作为AE 特征来研究骨料尺寸和应力水平对砂浆试件AE 的影响。Farnam 等人利用频率重心作为光谱参数，分析了水灰比变化时混凝土的声发射波形[6]。Carpinteriet 等研究了损伤对声发射参数的影响以及声发射波的衰减和散射，由于材料的非均匀性会导致强烈的畸变和衰减，因此要谨慎使用声发射的时域参数[7]。

混凝土是一种中观多相复合材料，且存在多尺度断裂过程。多尺度裂纹的分散能量耗散使得材料具有了准脆性特性。声发射技术可用于证明多尺度裂缝的发生过程，目前主要采用幂定律（古登堡·里克特定律）描述频率-振幅关系[8-9]。然而多尺度开裂只是混凝土复杂断裂过程的一个方面。更多的是要阐明断裂机制(裂纹桥接、分叉、闭合、终止等)、断裂模式(模式I 和II)，组分的非均匀性加剧了裂纹的多尺度扩展。因此，混凝土断裂过程也可称为多源、多机制、多尺度现象。

假设水泥基、粗集料和界面过渡区各种水化产物中发生的不同开裂现象以及施加的能量通量可能导致声发射光谱的差异响应。这样，随着损伤的发展，断裂过程的复杂性将体现在声发射光谱的无序性上。此外，相似的物质源发出的声发射信号的光谱含量大致相似，在保持低噪声水平和测量仪器效果相同的情况下，会产生相似的光谱紊乱。现有文献也证实了混凝土损伤通过瞬态应力变化时声发射谱的变化[10]。然而，经常被研究的频谱特征，如带宽、主频、谱心等，并不能代表声发射光谱中多频能量分布的复杂性。本研究的主要内容是在声发射信号频谱中寻找多源多机制断裂过程的痕迹，从而进一步分析混凝土损伤过程。为此，利用小波熵对声发射光谱能量分布的无序性进行了量化。小波熵是由小波变换分析频率子带的能量分布确定的。本研究中小波变换用于多分辨率光谱分析。

1 小波变换（WT）

任何模拟或数字仪器的原始信号通常都是在时域内采集的，需要对原始信号进行变换处理。数学变换的唯一目的是感知其他函数空间中的信息，以破译信号的生成过程。常用方法是用傅里叶变换将时域信号变换到频域以提取信号频谱信息。傅里叶变换将信号分解成复指数，复指数可以用正弦求和表示。由于正弦信号的频率具有良好的局域性，以正弦形式表示的信号在频域中有很高的分辨率。傅里叶变换在平稳信号幅频分析中的应用比较简单，但在非平稳信号时频分析中的应用比较复杂。短时间傅里叶变换(STFT)是一种常用的基于窗口内局部周期性的时域频率局部化方法。尽管不确定性原则为窗口长度提供了指导，但窗口选择仍然很困难。为弥补傅里叶变换的不足，小波变换在非平稳信号的时频定位中已经普及应用。小波变换中关键的缩放概念可概括为滚动的时间序列光谱通过一个数学显微镜。Grossmann 和Morlet 提出的小波变换理论通过对基函数进行伸缩和平移来进行尺度变换，以便将时频信号用多频带表示。小波分析的先驱Jean Morlet 引入了小波一词来描述任意平方可积实值函数，并将其用于地震时间序列分析。如今，小波分析不仅用于时频分析，还用于信号和图像的平滑和去噪、数据压缩、语音识别等多个方面。

信号X（t)对原型小波或母小波 ψ(t)的连续小波变换(CWT)定义为

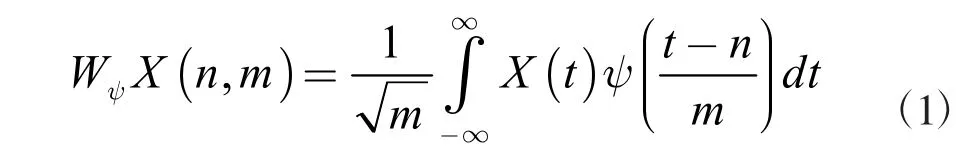
式中：m、n 分别为缩放参数和平移参数。式(1)是信号X（t)与缩放后的小波 ψ(t)离散形式的卷积。对信号X（t)的N个样本和K 级小波缩放，方程（1）产生了K 个长度为N的子信号。CWT 并不一定需要正交小波，由于使用任意尺度，变换后的数据高度相关。然而，连续的平移和缩放参数会导致过采样，这使得CWT 的计算成本很高。此外，CWT 更适合于信号的局部可微性分析和奇异性检测。对于离散信号使用CWT 也不可行。离散小波包变换(DWPT)通过一组离散的参数(a,b)克服了CWT 的高计算成本问题，这样信号就被分解成一组相互正交的小波。在实际应用中，DWPT 通过高通滤波器和低通滤波器的级联滤波器组实现。

2 离散小波包变换（DWPT）

DWPT 是对离散AE 信号进行多分辨率分解的有效方法。DWPT 也可以用公式(1)表示，但DWPT 用2 次幂的缩放值和平移值。m 和n 的值为m=2k，n=j·2k，其中k为层数，j 为每层的平移。DWPT 的本质是分别使用缩小采样和放大采样，通过一系列具有互补带宽的并进滤波器(低通滤波器和高通滤波器也称为正交镜滤波器对)对信号进行滤波。在任何级别的信号分解中，低通信号分量被称为近似信号，而高通信号分量被称为详细信号。因此，近似信号是信号的高尺度、低频分量。在第一级分解中使用的最小尺度对应于信号的最高频率。随着分解层数的增加，所需样本减少，信号采用缩小采样。由于输入信号频谱在每个分解层上的均分，DWPT 将输入信号的子带滤波变成更细的等宽区间。所得部分可以连续编号，称为节点。

2.1 相对小波能量

本研究利用离散小波变换将信号离散为子带。如果X（t)是AE 信号，则可以将其分解为分量X j1,Xj2, …,Xjk，其中j 为分解层数，k 为节点编号。一个节点表示信号的一个分解的分量(子)。这样在一个分解层上所有的节点分量相加就得到了原始信号。DWPT 到第三层的信号分层分解树见图1。每个节点的能量在第j 能级可以定义为E j1,Ej2, …,Ejk。因此，每一层相对于总能量的归一化能量为相对小波能量。

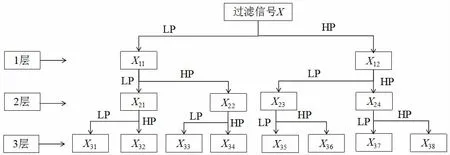
图1 小波包分解树

信号总能量为

考虑不同节点能量与总能量的比值，来确定不同分量的能量分布。因此，相对小波能量可以写成

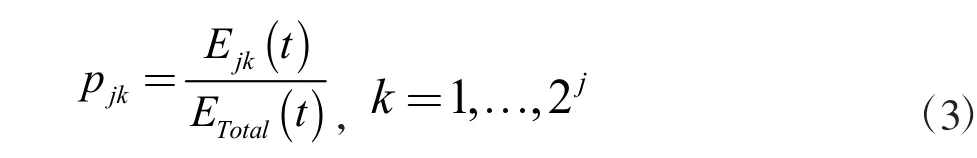
式中：pik为j 能级分解在k 节点的归一化能量比。

2.2 小波熵

式中，SWT为第j 层分解的小波熵，pjk为小波能量比。

小波熵的物理意义与香农熵相同。香农熵反映的是信息不确定程度。同样，小波熵也用于测量信号在不同频率子带中的能量分散情况。从物理学的角度来看，外部施加的能通量形成了材料中微缺陷处的内部应力集中，导致原子键的断裂，即裂缝。这些断裂的化学键发出高能振动(弹性波)，从而激发某些频率。来自多个化学键的多个弹性波的振动经过散射、反射、干涉和其他波现象，形成混合波形。传感器捕捉到的振荡类似于光谱域中城市或山脉的天际线，在不同的频率值上呈尖峰状，杂乱无章。利用多分辨率小波变换在频率子带中分离信号能量，可有效减少尖峰数量。这些应力波的能量也表现出几个量级的变化。因此，用信号总能量归一化频率子带能量，可以将所有信号归一化到同一个尺度上，在这个尺度上可以假设一个类概率函数。因此，小波熵分析了相对小波能量概率分布的无序性，在生物医学、电力系统、机械振动与故障检测、人工智能等领域的应用得到了广泛的应用。

3 结论

声发射光谱是混凝土多源多机制断裂过程的代表，该过程导致混凝土出现多尺度开裂。破裂过程的复杂性可以反映在声发射信号谱域的无序性上。因此，提出了利用小波熵作为声发射光谱无序度的定量度量方法。

利用小波变换对混凝土加载试验中获取的声发射信号进行分解，然后根据各频段归一化能量分布定义小波熵，体现了小波熵基于谱无序的信号识别能力。