Heisenberg 群中极小平移曲面的分类

朱尚书，杨潇阳

（东北大学南湖校区理学院数学系，辽宁 沈阳 110004）

1 预备知识

三维Heisenberg 群是带有左不变度量ds2=dx2+dy2+[τ（ydx-xdy）+dz]2的线性空间R3，其中τ∈{1}，被称为曲率参数，一般取值为1 或。在所有具有三次幂零性质的李群中，Heisenberg 群是最具有代表性的一个。这不仅仅是因为Heisenberg 群在群表示论方面的性质在三次幂零群中具有代表性，更重要的是物理学家认为Heisenberg 群和Heisenberg 李代数是研究量子力学的基本方程的理论基础。

令e1，e2，e3为Heisenberg 群中的标准正交基，则其李代数满足李括号：[e1，e2]=e3，[e2，e3]=0，[e3，e1]=0. 由标架e1，e2，e3可得Heisenberg 群上一组左不变标准正交基[1-7]：E1，E2，E3.该基底与自然基底∂x，∂y，∂z 之间的关系为：

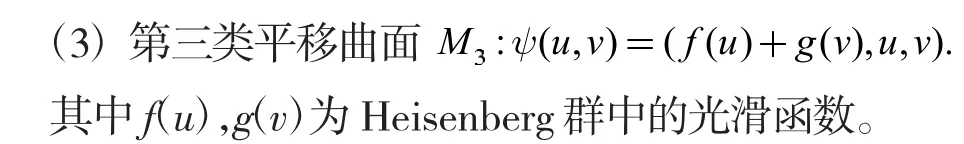
2 第一类平移曲面

本小节先讨论第一类平移曲面M1：r（u，v）=（u，v，f（u）+g（v））。直接计算可得：

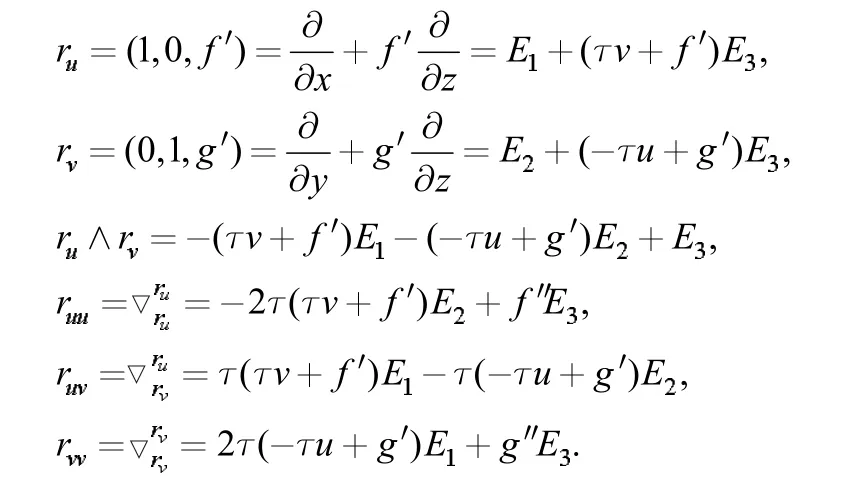
则的第一基本量为：

则有如下定理

定理1：对Heisenberg 群中第一类平移曲面M1:r（u，v）=（u，v，f（u）+g（v）），当曲面M1为极小曲面时，函数f（u），g（v）满足如下微分方程：

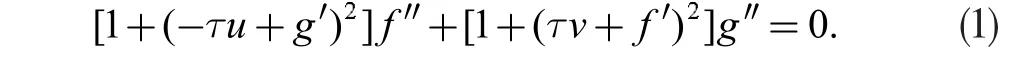
对H=0 式关于u，v 求偏导，得：

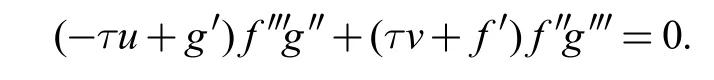
等式两边同除以f"g"，再对u，v 求偏导，可得：

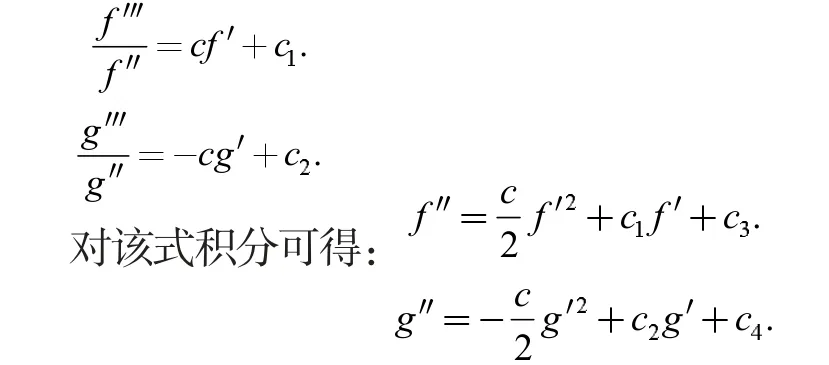
回代到H=0 的等式中，有：

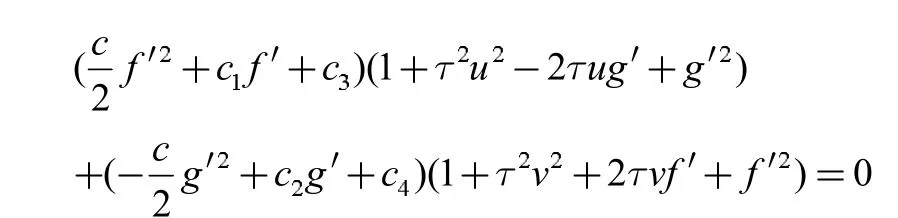
对其关于u，v 求偏导后，再对等式两边同除以f"g"后，再对其关于u，v 求偏导，

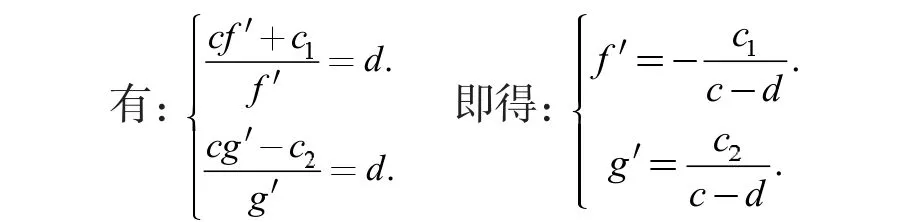
因该解二阶导为0，不符合题设条件，故所求函数f（u），g（v）不是H=0 的解。

将此解回代到H=0 的原式中进行验证，有：（cτv-c1）2=（c2-cτu）2，故该解是增根。

由于定理1 中的微分方程不能直接求解，下面将考虑该方程中函数f（u）所有的多项式特解。

情况3：设函数f（u）是关于u 的1 阶多项式，即f（u）=a1u+a0.将其代入等式H=0 可得等式：[（τv+a1）2+1]g"=0，因（τv+a1）2+1非负，故可得g"=0，即g 是有关v 的一阶多项式。

情况4：设函数f（u）是0 阶多项式，即f（u）=a0是个常数。将其代入等式H=0 可得：（τ2v2+1）g"=0，因τ2v2+1非负，故可得g"=0，即g 是有关v 的一阶多项式。

综上所述，则有如下命题：

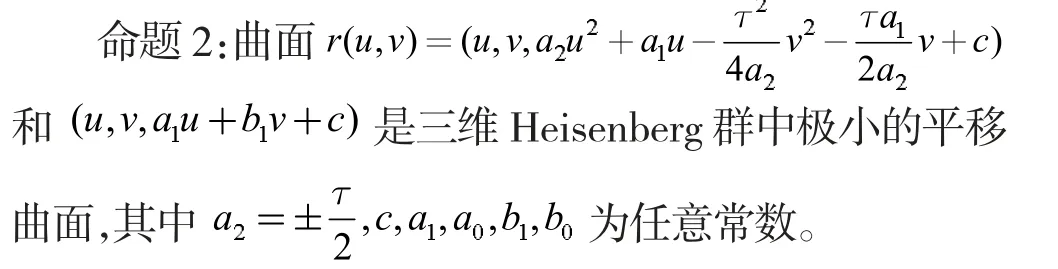
图1 是三维Heisenberg 群中第一类平移曲面里一个极小曲面的图形。

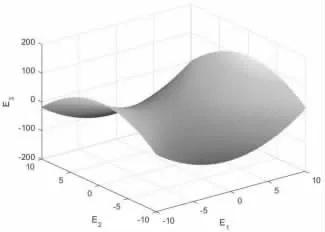
图1 （u，v，u2+u-v2-v）

3 第二类平移曲面

本小节讨论第二类平移曲面M2：φ（u，v）=（u，f（u）+g（v），v）。直接计算可得：

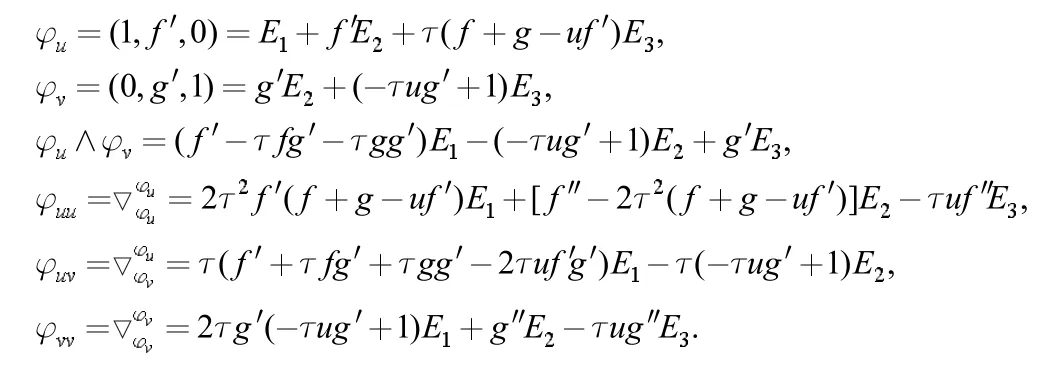
则M2的第一基本量为：

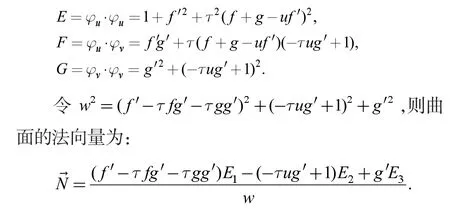
第二基本量为：

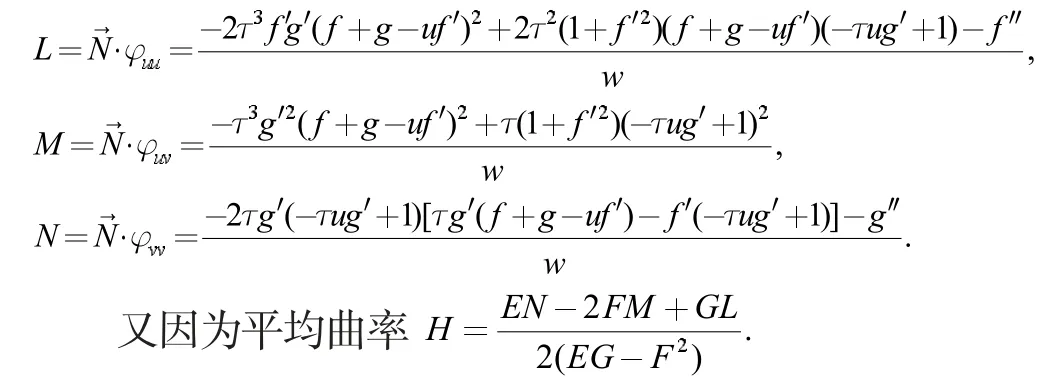
当H=0 时，可得微分方程：

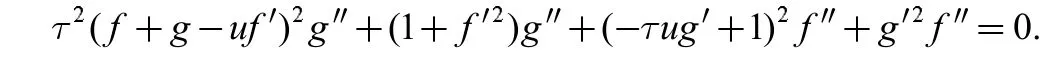
则有如下定理

定理3：对Heisenberg 群中第二类平移曲面M2：φ（u，v）=（u，f（u）+g（v），v，当曲面M2为极小曲面时，函数f（u），g（v）满足如下微分方程：

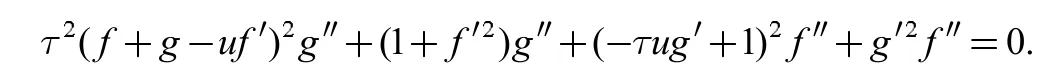
由于定理3 中的微分方程不能直接求解，下面将考虑该方程中函数f（u）所有的多项式特解。

图2 是三维Heisenberg 群中第二类平移曲面里一个极小曲面的图形。由图发现，其多项式解只有平凡解。

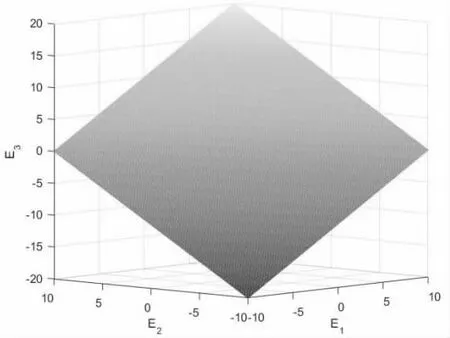
图2 （u，u+v，v）

4 第三类平移曲面

本小节讨论第三类平移曲面M3：ψ（u，v）=（f（u）+g（v），u，v）。直接计算可得：

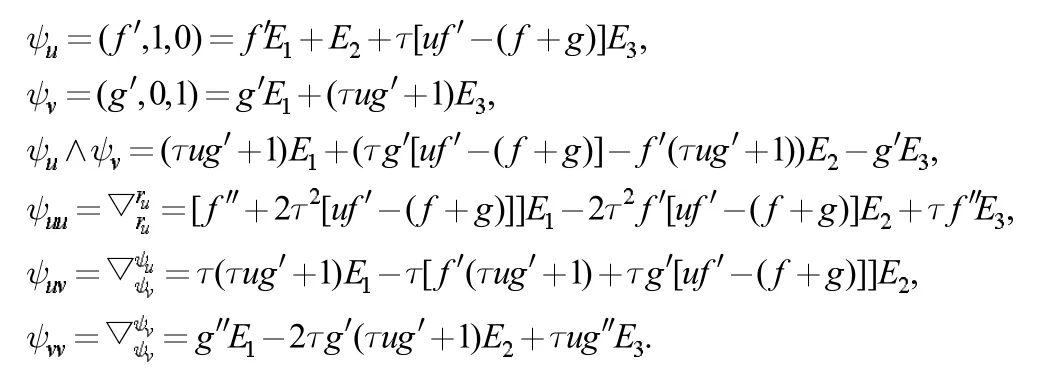
则M3的第一基本量为：

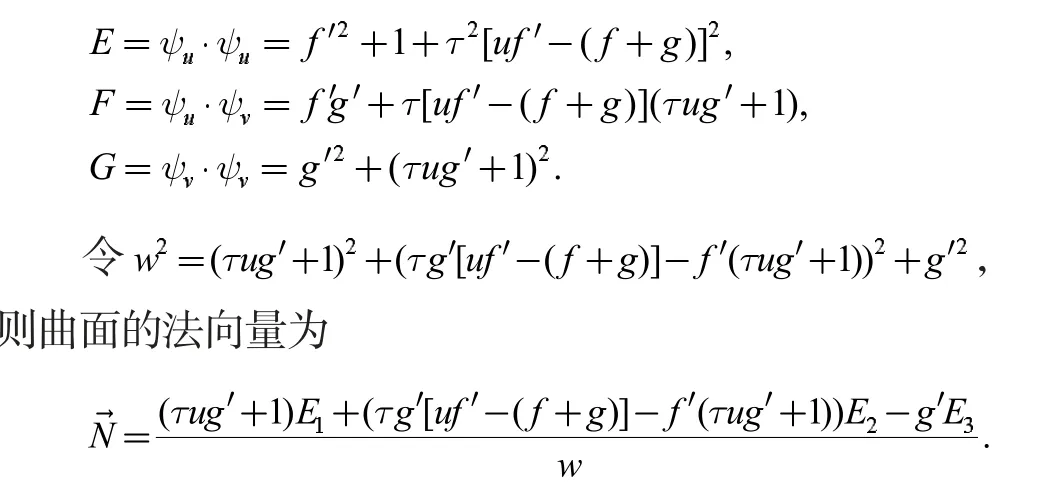
第二基本量为：

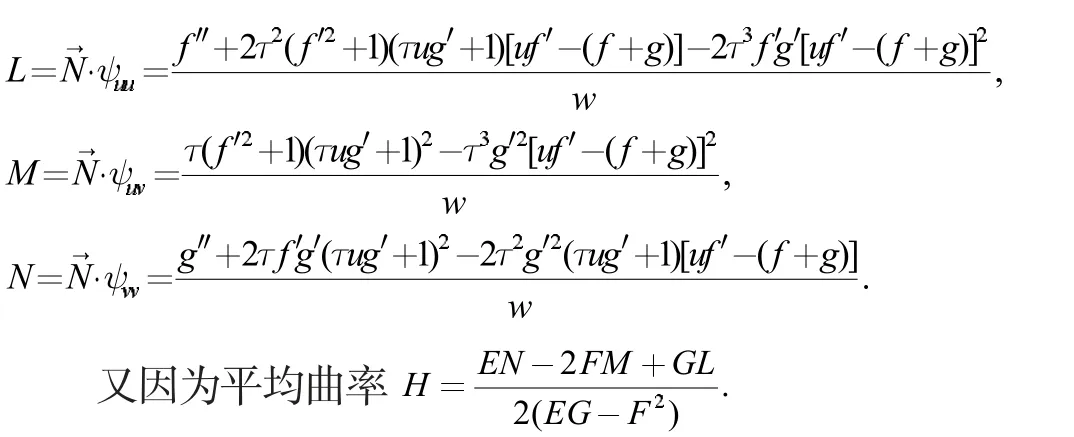
当H=0 时，可得微分方程：

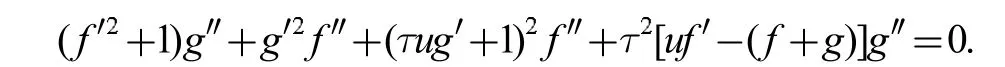
则有如下定理

定理5：对Heisenberg 群中第三类平移曲面M3：ψ（u，v）=（f（u）+g（v），u，v），当曲面M3为极小曲面时，函数f（u），g（v）满足如下微分方程：

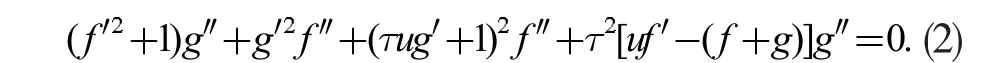
由于定理5 中的微分方程不能直接求解，下面将考虑该方程中函数f（u）所有的多项式特解。

图3 是三维Heisenberg 群中第三类平移曲面里一个极小曲面的图形。

图3 （u+v，u，v）

由图3 可知，这也是个平凡解。

5 结论

本研究在三维Heisenberg 群中讨论了平移曲面。因为该群中的度量对于坐标不具有对称性，所以文中分别对三种类型的平移曲面进行了讨论，得到了三种平移曲面为极小曲面时的函数应满足的微分方程。由于计算量大，平均曲率的方程过于复杂，所以目前只对极小的平移曲面进行了分类，而没有找到更好的方法对具有常平均曲率的平移曲面进行分类。接下来需要考虑的是，如何从已得的微分方程求出所有非增根的解，以及讨论方程是否其存在非多项式的解。