求不定积分的常用技巧方法

◎李东方 胡梦薇

(河南省许昌市许昌电气职业学院公共教学部，河南 许昌 461000)

不定积分是积分学的重要组成部分，也是微积分的核心学好不定积分对后续积分学的学习至关重要求不定积分的方法有很多，主要有直接积分法、第一换元积分法、第二换元积分法、分部积分法为了更好地学习不定积分，我们不仅需要掌握基本的求解方法，而且要掌握一定的技巧，这样才能在求解不定积分时思路开阔，灵活解题在本文中，笔者依据多年的教学实践，结合被积函数的特点，介绍几种常用的求不定积分的技巧

一、第一换元积分法

由于此方法将′()d凑成微分d()=d，所以它也叫作“凑微分法”应用凑微分法的关键是把被积函数表达式凑成[()]d()的形式

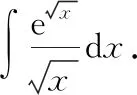
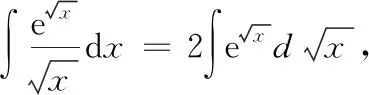
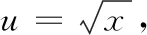
在凑微分时，要具体问题具体分析同学们应在熟记基本积分公式和常用凑微分式子的基础上，通过不断练习，掌握这一重要的积分法

二、第二换元积分法

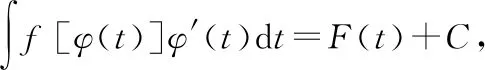
其中=()是=()的反函数

应用第二换元积分法的关键在于合理选取变量代换=()，消去被积函数中的根号，使积分计算简单化

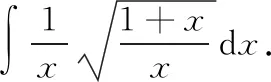
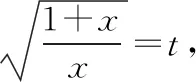
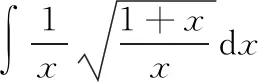
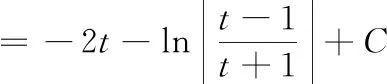
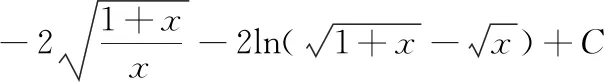
三、分部积分法

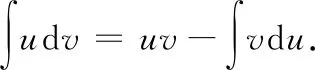
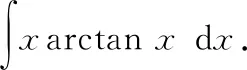
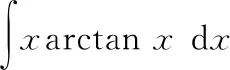
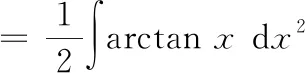
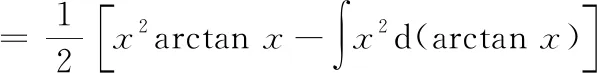
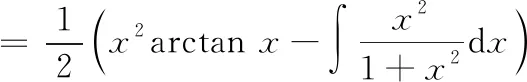
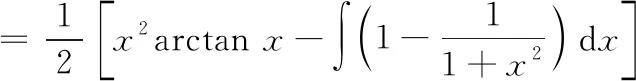
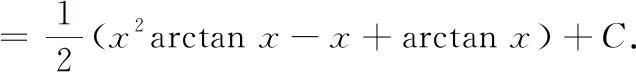
运用分部积分法时，恰当选取和d是关键一般地，“对反幂三指(对数函数、反三角函数、幂函数、三角函数和指数函数)”，两者之间排在前面的设为

四、最小公倍数法

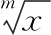
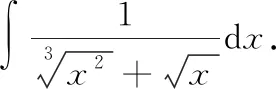
令=[,]=，则d=6d，从而有

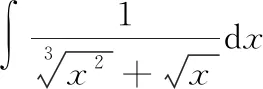
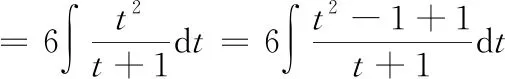
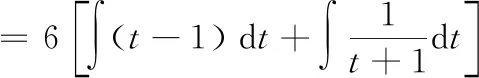
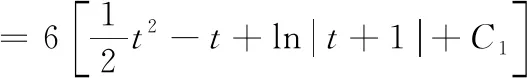
=3-6+6ln|+1|+

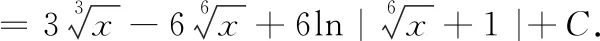
五、整体凑微分法

凑微分法是求不定积分的重要方法之一一般的凑微分法是利用基本微分公式解题，而整体凑微分法是根据被积函数的特点，将整个式子凑进去，从而使问题得到解决的一种方法

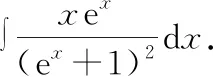
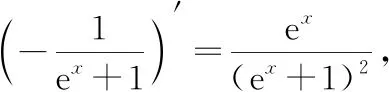
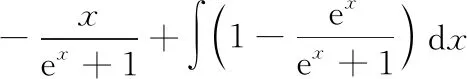
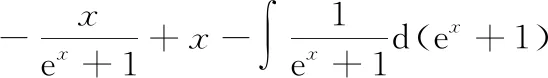
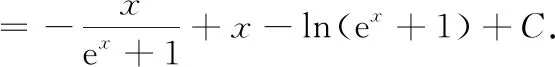
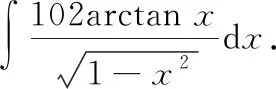
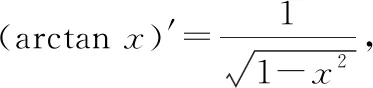
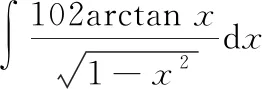
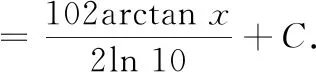
六、方程组法

当被积函数是一些特殊的分式时，我们可以构造与其关联的另一个不定积分，然后通过解方程组进行计算

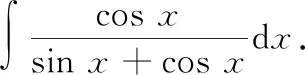
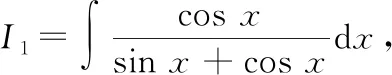
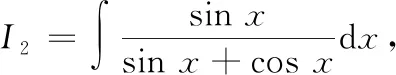
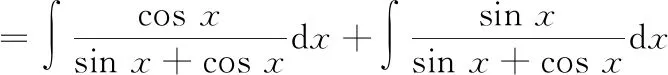
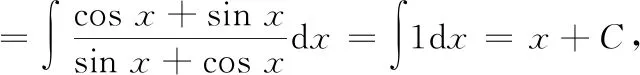
①

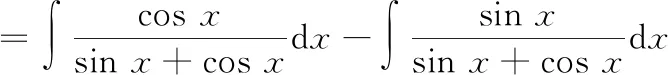
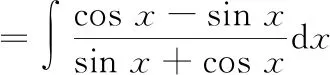
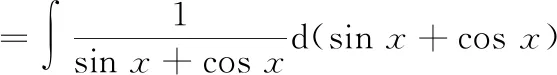
=ln|sin+cos|+

②

联立①②,解方程组可得

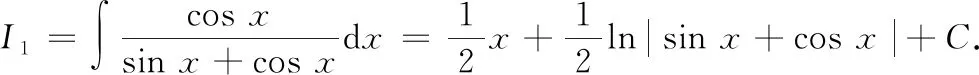
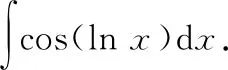
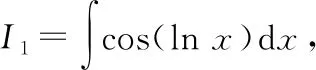
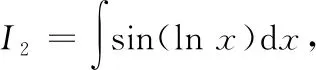
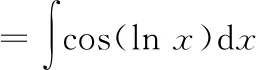
=cos(ln)+,

①

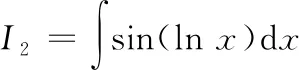
=sin(ln)-

②

联立①②,解方程组可得

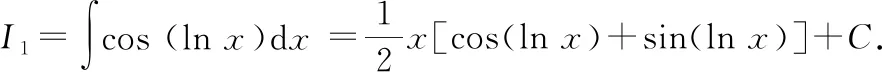
七、分部循环法

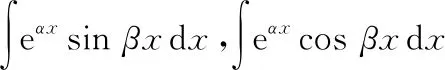
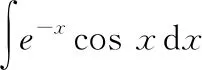
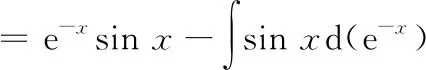
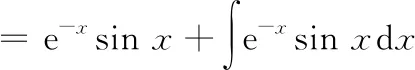
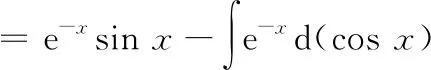
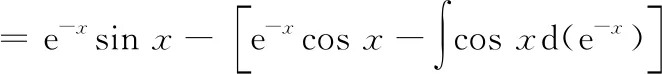
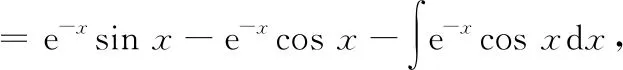
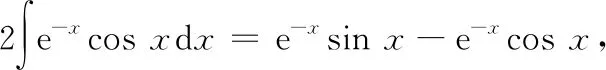
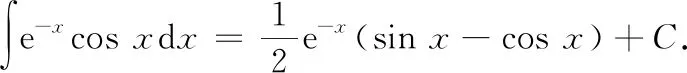
八、恒等变换法

若被积函数中含有三角函数，则往往利用三角恒等变换将被积函数进行变形，进而求解不定积分

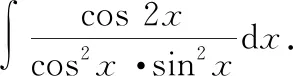
考虑到cos 2=cos-sin，我们对被积函数进行恒等变换如下：

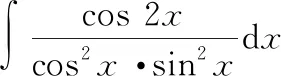
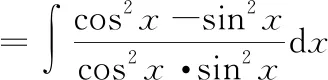
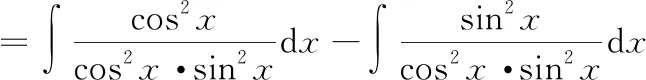
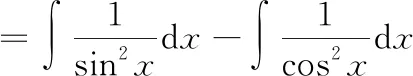
=-cot-tan+

九、添项相消法

添项相消法是求解不定积分的一种常用技巧，一般方法是根据被积函数的特点进行加项、减项或者乘项、除项

根据被积函数的特点，分子、分母同乘e，得

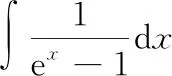
=ln(e-1)-+

十、部分相抵法

部分相抵法是将所求不定积分分解成两个不定积分的和或差，在计算不定积分的过程中部分积分可以相互抵消的一种方法

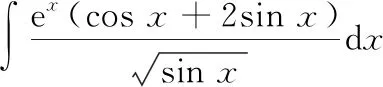
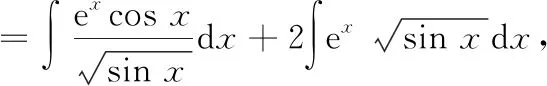
先计算第一个不定积分，由分部积分法可得

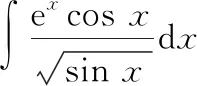
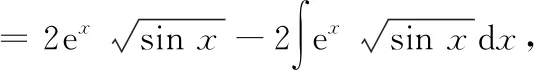
运用分部积分法之后，出现了第二个不定积分的形式，可以相互抵消，所以

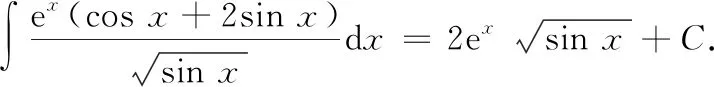
十一、欧拉(Euler)变换法

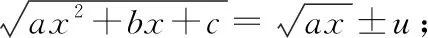
我们将上述变换称为欧拉(Euler)变换

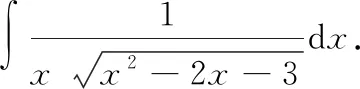
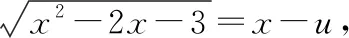
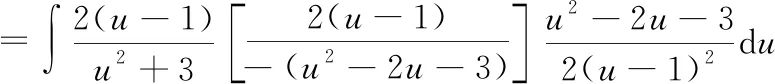
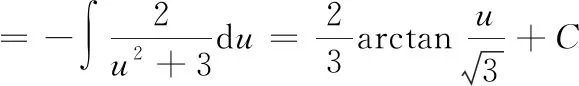
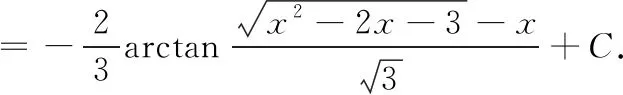
十二、商的不定积分法

设函数()，()在区间上有连续导数，并且()，′()在区间上不恒为0，那么：

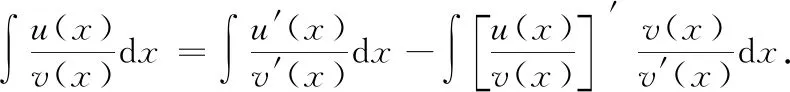
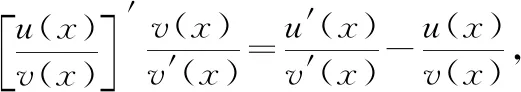
上式两端求不定积分，可得

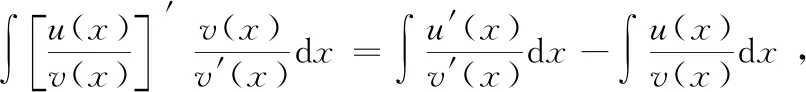
移项，可得

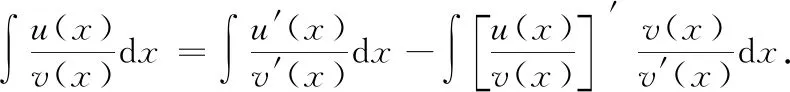
运用商的不定积分法，通过计算导数，可以简化被积函数，降低难度下面我们通过具体例子来说明此方法的应用

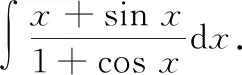
通过观察被积函数，由商的不定积分法可得

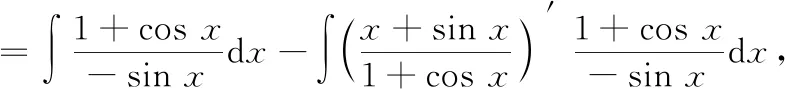
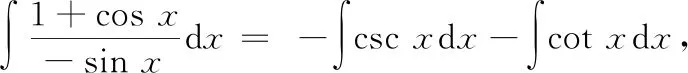
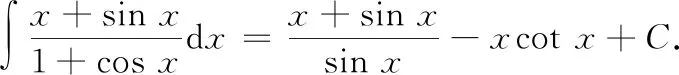
十三、结束语

本文通过经典样例给出了求解不定积分的常用技巧方法，可见不定积分的计算方法灵活，技巧性强，形式多种多样在求解不定积分时，我们要具体问题具体分析，善于归纳总结，融会贯通，这样才能为后续定积分内容的学习奠定一个良好的理论基础