用技术手段进行前置性补偿教学的实践——以“用一次函数解决问题(第1课时)”为例

◎钱海峰

(江苏省南京市紫东实验学校，江苏 南京 210000)

近期，笔者参加了南京市新优质初中发展联盟学校“技术支持下的精准课堂教学”专题研讨会议，并执教“用一次函数解决实际问题(第1课时)”本节课位于八年级上册第六章第四节，是函数解决问题的初步介入，因此学生有些陌生；本节又放在一元一次方程和一元一次不等式的学习之后，因此学生有一定的基础本节课主要体现了数形结合、转化等数学思想和数学方法，对学生基本数学思想和素养的形成起推动作用笔者利用一个或者两个一次函数与一元一次方程、一元一次不等式等知识之间的联系来解决实际问题，使学生能更好地将所学知识融会贯通以下是笔者执教该课的教学实录

一、教学实录

(一)极算前测，了解学生掌握知识的程度

题目设置：

1汽车油箱中原有汽油6 L，给汽车加油的加油枪流量为25 L/min，设油箱中的油量为(L)，加油时间为(min)，则函数表达式为

2一盘蚊香长105 cm，点燃后每小时缩短10 cm，设蚊香燃烧后剩余的长度为(cm)，燃烧时间(h)，则函数表达式为，蚊香可燃烧h

3探测气球从海拔5 m处出发，以1 m/min的速度上升，气球所在的海拔(m)关于上升时间(min)的函数表达式；当满足时，气球不超过55 m

极算结果：

八年级(4)班测评报告课题:“用一次函数解决问题”前测时间:12月11日16:50-16:55全班成绩概况初次平均分最高分平均耗时84.9分100分3'59″成绩分布0～59分60～79分80～89分90～100分3人10人0人27人答题情况第1题第2题第3题90%92%72%知识点薄弱情况薄弱一般较好21118

前测的主要目的是进行本堂课学习的知识储备，让学生会通过实际问题写函数关系式，并再次回忆函数与方程、不等式之间的关系：这三个选题在前面的课堂中已经出现过，而且都是一个函数表达式，所以在难度上应该不是难题从学生测试报告中可以看出：在实际问题中，给出变量写函数关系式有一定的基础，但是将一次函数转化成不等式解决问题存在困难

(二)选择评讲，回顾从实际问题写函数关系的方法(用时3分钟)

王可欣的试卷曹宁雅的试卷1.汽车油箱中原有汽油6 L,给汽车加油的加油枪流量为25 L/min,设油箱中的油量为y(L),加油时间为x(min),则函数表达式为 .初次答案:y=25x ✕重做答案:y=25x+6 正确答案:y=6+25x3.探测气球从海拔5 m处出发,以1 m/min的速度上升,气球所在的海拔y(m)关于上升时间x(min)的函数表达式 ,当x满足 时,气球不超过55 m.第1空初次答案:y=x ✕重做答案:未作答正确答案:y=x+5

问题1：这两个同学函数关系式写错的原因是什么？

学生1：他们没有找准题中关于变量的相等关系

追问：正确的相等关系是？

学生2：油箱中油量=原有油量+加入油量

问题2：如何正确地写出函数关系式？

学生3：先找两个变量，再找出与变量有关的相等关系

(三)课堂小测，了解学生复习效果(用时3分钟)

题目设置：

1汽车以60 km/h的速度匀速行驶，行驶路程为，行驶时间为，这个变化过程中的函数表达式：

2汽车油箱中有汽油50 L，如果不再加油，那么油箱中的油量(L)随着行驶路程(km)的增加而减少，耗油量为01 L/km这个变化过程中的函数表达式：

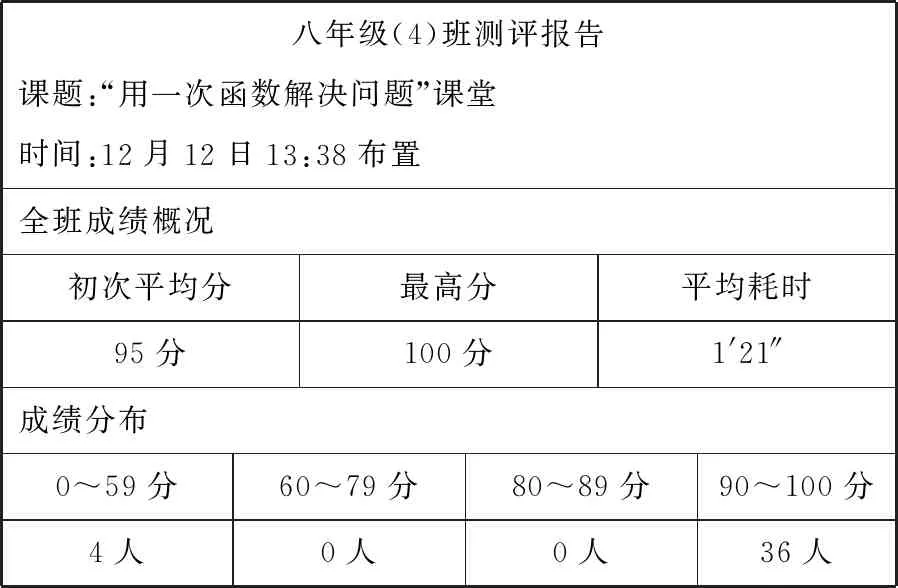
八年级(4)班测评报告课题:“用一次函数解决问题”课堂时间:12月12日13:38布置全班成绩概况初次平均分最高分平均耗时95分100分1'21″成绩分布0～59分60～79分80～89分90～100分4人0人0人36人

两次成绩对比

教师针对学生前测的部分情况，消除学生从实际问题写关系式的障碍，平均分也从849分上升至95分，其中4个学生中有2个稿纸上的答案完全正确，因操作问题而导致错误同时，本环节是为下面不给变量写函数关系做铺垫

(四)不给变量从实际问题中找出变量，写出函数关系式(20分钟)

设置问题：、两地相距140 km，甲车以60 km/h的速度匀速从地驶往地，同时乙车以80 km/h的速度从地驶往地

(设问1)：你能从这个变化过程中发现几个变量？把它写下来！

(设问2)：你能从中选择两个变量建立函数表达式吗？把它写下来！

(设问3)：你能提出一个问题用你写的一个或者两个函数关系式解决吗？4人小组选择一个完成并与他人分享

(选取两个小组试卷还原)

小组1试卷还原【问题】A、B两地相距140 km,甲车以60 km/h的速度匀速从A地驶往B地,同时乙车以80 km/h的速度从B地驶往A地.解:变量有时间、甲行驶的路程、乙行驶的路程,关系有:甲行驶路程=甲行驶的时间×行驶的速度,y1=60x.乙行驶路程=乙行驶的时间×行驶的速度,y2=80x.问题:(1)两车行驶多长时间相遇?(2)行驶2小时,两车各行驶了多远?解:(1)140=60x+80x,x=1.答:经过1小时两车相遇.(2)当x=2时,y1=60x=120,y2=80x=160.答:2小时甲车行驶了120 km,乙车行驶了160 km.小组2试卷还原【问题】A、B两地相距140 km,甲车以60 km/h的速度匀速从A地驶往B地,同时乙车以80 km/h的速度从B地驶往A地.解:变量有时间,甲离A地的距离,乙离B地的距离,甲离B地的距离,乙离A地的距离,甲、乙相距的距离.问题:(1)请写出两车相距距离与行驶时间的函数关系式.(2)行驶2小时后两车相距多少?解:设甲乙出发后的时间为x h,甲、乙相距的距离为y km(1)当甲、乙相遇前时:y=140-60x-80x=-140x+140,当甲、乙相遇后时:y=60x+80x-140=140x-140.(2)因为两车1小时的时候相遇,当x=2时应代入y=140x-140=140×2-140=140. 答:出发2小时,两车相距140 km.

这个环节是本堂课的关键部分，很多学生不会用函数解决问题的主要难点就是不会寻找变量我们需要给学生时间和空间去思考学生静心思考会有很多惊人的答案比如，有的学生选择车辆之间的距离和行驶时间做变量；有的学生在写关系式时用线段图分析量的关系，有了图的支撑，就比较容易写函数关系式了；有的学生用一个函数关系式，也有的学生用两个函数关系式，但是在解决问题没有顾及实际情况的取值范围，如2小时两车行驶的路程，全程共140千米，2小时乙车怎么可能行驶160 km不过这些问题也为笔者后面将函数关系式转化成方程和不等式来解决实际问题埋下伏笔

(五)利用函数关系式解决实际问题

设置问题：

现有两种移动电话每月的计费方式：

方式一：月租费30元，本地通话030(元分钟)

方式二：无月租费，本地通话040(元分钟)

(设问1)设方式一的每月费用为元，方式二的每月费用为元，通话时间为h，写出两种方式的函数关系式

(设问2)上述两种套餐中，哪种比较合算？

本环节其实是一个联系的过程，有了前面的环节做基础，学生会写函数关系式，会通过相等关系和不等关系将函数关系式转化成方程或者不等式，解方程或不等式从而达到解决问题的目的

(六)课堂小结

(多个学生总结)一次函数也是一种解决实际问题的数学模型，首先我们要学会从实际问题中寻找有相等关系的两个变量，写出函数的关系式，再通过问题中的数量关系将它转化成方程或者不等式，从而达到解决实际问题的目的

二、教学反思

初中数学教学效果的展现对逻辑思维能力、学生课堂参与度要求较高教师如果只是单方面根据课程进度和要求，忽略学生的主导地位而设计课程内容，则效率明显不高这样，学生无法达到打开思路的目的，老师无法达到精准教学的目的前置性补偿教学的教学设计是一种以学生为本的教学思路展示，这种方法很好地改变了这种局限性第一，学生可以预习课程，了解本节课与哪些已学知识相关，自然而然地对本节课产生知识或方法迁移的效果；第二，可以把课堂的主体地位和主动权交给学生，真正达到“以生为本”的教学理念，从而提高课堂效率；第三，教师通过前置性补偿教学，也可以了解学生学习本节课内容时，还有哪些知识和方法缺失，在课堂上由浅入深，逐个突破，从而达到精准教学的目的

精准教学是由奥格登·林斯利于20世纪60年代基于斯金纳的行为学习理论提出的方法最初，旨在通过设计测量过程来追踪小学生的学习表现和支持数据决策，以便“将科学放在学生和教师的手中”后来发展为用于评估任意给定的教学方法有效性的框架作为精准、系统的评估方法，精准教学兼容于各种教学策略，可对任何学科、任何学段的教学进行评估

在早期的精准教学中，教师和学生在教学和实践过程中通常使用铅笔一次一个点地记录学生的表现，并以此进行人工分析与决策华东师范大学祝智庭教授讲过:信息技术支持的高效知识教学可以激发精准教学的活力，同时可以减轻教师平时的教学负担所以在应用App、流媒体、多媒体、大数据的社会，我们可以借助信息技术进行各种诊断，然后针对不同的学生进行精准教学

结合以上两个想法，笔者在本堂课中应用了极算软件进行了前测，通过大数据进行分析，可以准确地让教师了解学生在本节课前已经掌握的知识水平，存在什么弱项，也为教师下一步教什么、怎么教提供了依据当然，精准教学除了在内容上、目标上定位精准，我们还要在时间上把握精明、方法上手段精致如，笔者在本节课采用了数字实时互动板，让所有学生的书写都实时地反映在黑板上，笔者可以通过学生的书写情况进行及时的帮助和选择性的讲解

运用精准教学的最大意义在于能够更加准确地对学生在数学学习过程中所出现的关于基础知识或者是学习能力的问题进行教学，进一步保证教学的精准度教学中的问题是指给定信息和方针之间存在着某些障碍，针对详细问题的教学能够多、快、好、省地完成教学任务,实现精准教学而大数据时代下，我们可以利用信息技术做到这种“多、快、好、省”的要求

波利亚说：“掌握数学就是意味着善于解题”这里的“掌握”包括掌握关于数学的知识的意蕴、思考方式、思想方法、思维倾向等我们要让学生在考试中会解题，那么我们在平时的教学中对于学生的现有水平、思考方法和思考方式的认知必须精准，这样才能真正提高学生的课堂学习效率，提高学生的数学素养