MATLAB在“大学物理”课程学习中的应用

黄旭初，李艳青

（昌吉学院 物理系，新疆 昌吉 831100）

“大学物理”是理科、工科、农学和医学专业的基础课程，其内容覆盖范围广、知识较为抽象，并且在学习过程中需要一定的数学知识，这给广大学生的学习带来了一定的困难。对于一般的本科院校来说，“大学物理”这门课通常是开设在大学的第一学年，基本上与高等数学同步开设，然而在这个阶段，大多数学生利用积分、求导、极限等数学工具解决物理问题的能力略显不足。由于数学知识的薄弱，导致学生无法很好地理解物理问题，这极大地削弱了学生对物理的学习兴趣。针对这个问题，通过课程改革取得了一定的成效，例如，用混合教学将线上和线下相互结合，调整教学内容和教学方法等。然而，大学物理知识具有较强的逻辑关联性，知识结构环环相扣，同时这门课是训练学生思维方式的一个过程，因此，从形式上或者结构顺序上的调整仍无法从根本上解决这个问题。为此，我们提出利用一些科学软件来辅助学习，这不仅能够克服数学上的障碍，同时还能将抽象的物理问题形象化，进而抓住物理的本质，加深对物理问题的理解，从而能够有效地提高学习效率，激发学生的学习兴趣。

目前，常见科学软件有Mathematic、MATLAB、Excel等，其中MATLAB以简单易学、函数丰富、数形结合便捷等优势被广大师生所青睐。由于MATLAB包含较为完善的数学函数，编程语言通俗易懂，学生容易掌握，因此利用MATLAB辅助学习大学物理成为可行。如何利用MATLAB处理大学物理中的物理问题，将物理问题图形化是提高学习兴趣的关键，本文就围绕这个问题选取力学、电磁学和机械波的相关知识点展开论述。

一、“大学物理”中的数学问题

在大学物理的知识结构中，质点的运动及其运动规律是最为简单、最基础的章节，在这个章节中部分学生对位移、速度和加速度这三者之间相互关系的理解停留在高中的阶段，也就是会用一些现有的公式来处理质点的运动问题。用以前学过的知识处理质点运动问题，这说明学生对相关数学知识的理解和应用欠缺，导致的结果就是思维方式没有发生转变，在后续的学习过程中就变得非常吃力，从而觉得大学物理很难，逐渐失去对大学物理的学习兴趣。在质点的运动章节中应用的数学知识主要是求导、积分和极限，如果能够把这些知识点的物理和数学之间的关系理解清楚，就能在后续的学习过程中得心应手。

对于极限在质点运动中的应用主要是体现在平均和瞬时之间的关系上，如瞬时速度是将平均速度的时间取极限，从物理角度来理解就是时间点和时间段的变化。用MATLAB来取一个函数的极限可以用limit（r,t,0）的形式直接调用，其中r表示位置矢量函数，t是时间参量，0表示让时间变量t无限趋近于零。例如已知运动一质点沿着x轴运动的位置和时间的关系由方程x=50t+5t确定，求质点在最初3秒内的平均速度和质点在t=3s时的瞬时速度？对于这样的问题，平均速度可以按照定义在MATLAB中输入v=（50*3+5*3^2-0）/（3-0）直接计算，瞬时速度就可以用v=limit（（50*t+5*t^2-50*3-5*3^2）/（t-3）,t,3）计算。如果按照数学中导数的定义，将平均速度中时间的变化量取极限就是位移对时间的导数，即=/就是瞬时速度，那么这个问题在MATLAB中就可以更为简便的直接调用导数函数v=diff（50*t+5*t^2,1），在获得任意时刻的瞬时速度v=50+10*t基础上，代入t=3s求得答案。

在“大学物理”课程中对于导数的应用，主要体现在考察两个变量之间的对应关系上，例如位移随时间的变化、动量随时间的变化和热量随温度的变化等。对于这个知识点的学习，学生遇到的问题主要有两点：第一，对于导数的基本公式没有很好的掌握，在应用的时候拿不准，需要查阅记分表，特别是在复合求导和偏导数计算中容易出错；第二，由于在高等数学中导数的定义是建立在标量基础上，对于矢量的求导学生不太容易理解。在“大学物理”教学过程中，为了能够让学生更好地理解矢量的求导，通常是将导数用极限的形式表示出来，考虑变化矢量的大小和方向在取极限条件下随另一个物理量之间的变换关系。如在质点的圆周运动中，切向单位矢量对时间的导数d/dt，可以写成lim（|Δ|）n/Δt=（/R）n，学生很难理解为什么切线方向的单位矢量求导会转到法线方向。MATLAB软件的基础是函数的矩阵表示，矢量用矩阵形式计算是非常便捷的，从而我们可以用MATLAB对这个问题做一个简单的说明。假设切线方向初始单位矢量A=［cosθ,sinθ］，末态单位矢量为B=［cos（θ+Δθ）,sin（θ+Δθ）］，则单位矢量的变化量C=B-A=［cos（θ+Δθ）-cosθ,sin（θ+Δθ）-sinθ］。要确定两个矢量相互垂直，只需要证明它们的点乘为零，用MATLAB可以调用limit（dot（C,B）,Δθ,0）或 者limit（dot（C,A）,Δθ,0）来得到这个结果。这样处理一方面加深了对极限和导数的理解，另一方面简化了矢量的运算，从而让学生不再为数学问题所困扰，而更加关注对物理问题的理解。

积分在大学物理中的应用非常广泛，但是学生在学习过程中却比较吃力，主要是因为学生记不住积分公式，或者对于积分的上下限模糊不清。由于积分是相对于导数的逆变换，所以在大学物理中只要有求导通常都会出现积分，并且积分变换后拥有相应的物理含义，例如牛顿第二定律F=dP/dt，这个式子原本表示的是动量随时间的变换关系，经过积分变换后ΔP= Fdt就表示质点的动量定理。在大学物理中积分可以理解为取极限情况下对某一个物理量的求和，而积分上下限对应的是边界条件，结合MATLAB就很容易克服积分带来的困扰。在质点运动章节中，例如已知质点沿x轴直线运动，加速度为=4-（/），初始条件=3时，=2/，求质点的速度。由加速度的定义可以得到=（4-），对这个式子两边同时积分就能得到速度的表达式=+4-/3，参量是通过带入初始条件求得。应用MATLAB可以调用int（1,v,v0,v）和int（4-t,t,0,t）对两边进行积分，获得任意时刻速度的表达式。当然，这样简单的函数应用MATLAB似乎没有太多的简化，然而面对一些复杂的函数时，MATLAB的优势就会显现出来。学生在学习过程中，从质点的运动开始能够逐渐用MATLAB辅助学习，能够很好地起到过渡作用，随着数学和物理知识的逐步深化，处理复杂问题的能力也会逐步增强。例如在热学部分和电磁学部分不仅会用到极限、导数和积分这样一些知识，还会用到级数展开，特殊函数及微分方程的求解等知识，同样这些问题也能结合MATLAB进行处理。

二、物理问题的图形处理

在学习过程中，通常图形与复杂的数学公式相比更为直观、具体，对于物理问题的理解也更容易一些。MATLAB不仅能够对一些函数直接调用，同时还能够将这些函数用图的形式展示出来，综合了计算和画图功能，这使得能够更为直观的分析物理问题。下面我们通过两个较为抽象的物理问题为例，探讨如何应用MATLAB将抽象的概念图形化，分析相应的物理本质。电磁学章节中电场和电势的分布，仅通过点电荷的电场强度和电势公式很难看出它们的分布情况，对于电场强度和电势之间的关系也不容易掌握。然而，将点电荷电势的公式直接输入到MATLAB中，并且调用梯度函数gradient，等值线函数contour和矢量函数quiver就能将电势和电场强度之间的关系很好的展示出来，如图1所示。

图1 等电量的三个点电荷周围电场线和电势分布图，（a）和（b）分别表示三个异号电荷和同号电荷的电场线和电势分布情况

在做“大学物理”实验中，描绘多个点电荷的电场线让多数同学都感到很困难，通过这样一个辅助计算就可以将理论和实验紧密结合起来，从而更加主动地思考更深层次的一些物理问题。从图1中我们可以看到在x-y平面中，空间各点的电场强度我们都可以用一个具有一定长度的箭头来表示。从箭头的方向可以反映出电场强度在空间各点方向的变化。基于电场强度和电势的关系，可以从等势线的疏密程度看出电场强度的大小。由于模拟过程中是按照相等的电势差为单位间隔，从而我们可以看到靠近电极位置等势线密集反映出较大的电场强度，较远的地方稀疏反映出较小的电场强度。

在机械波的学习中，波的叠加和干涉都是通过数学计算，然后对相应的物理量进行分析，从而研究波的性质。对于波的性质研究，用MATLAB画图是比较方便的，例如用mesh对相干波进行画图，能够很直观地看到空间各质点的振动情况，振动加强和振动减弱点的位置及它们与波源、频率、波长等参量的关系都能清晰地展现，如图2所示。

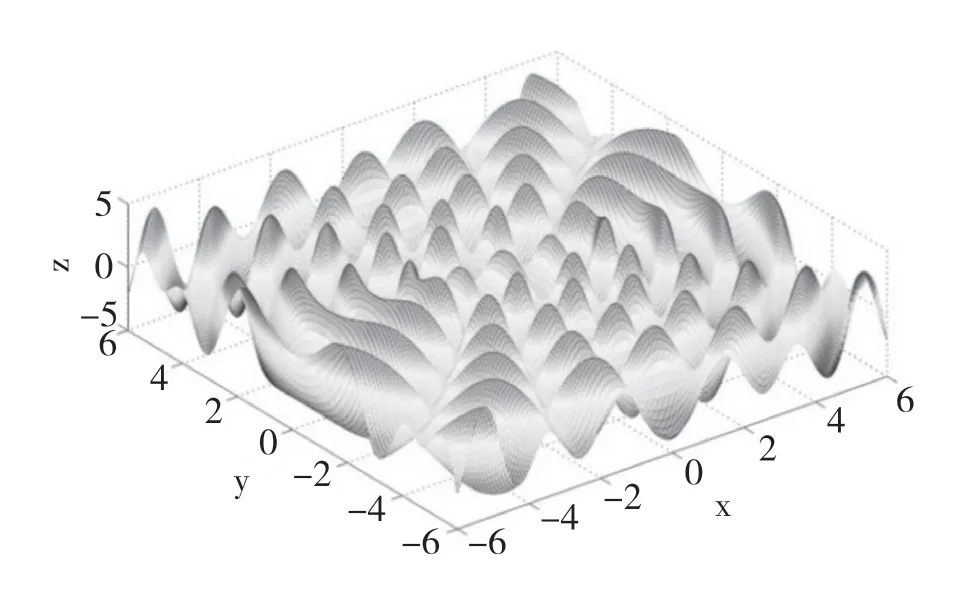
图2 波源分别位于x-y平面（2，0）和（-2，0）两点的两相干波的干涉图样

在用MATLAB对相干波进行表示的过程中，不需要复杂的计算，学生可以通过修改波长、频率或者传播方向等参量来研究不同情况下波的图样。这里我们是选取了波源位于x-y平面（2，0）和（-2，0）的两点。从图上我们可以看到，在z方向振幅出现了明显的加强和减弱现象，而且这种振幅的变化呈现一种对称分布。通过调整参数如改变波源的位置，或者用球面波或者柱面波就会使得干涉图样呈现出其他的变化形态。在“大学物理”中用MATLAB把物理问题图形处理的优势就省去了复杂的计算，可以直观的研究物理问题，并且把物理问题进一步的深化。例如机械波的问题可以适当地扩展到电磁场的传播，或者是光学的关涉等问题。这种用MATLAB图形研究物理问题，随着大学物理知识由浅入深的学习，对于培养相关专业学生的思维能力和创新能力有很大的提升，同时，克服了物理问题抽象化给学生带来的困扰。

三、应注意的一些问题

应用MATLAB辅助大学物理的学习具有很多优势，然而，在分析具体的物理问题时要考虑到软件的局限性，分清编程语言和物理问题之间的联系和区别。在应用MATLAB处理物理问题过程中，要注意三方面的问题：第一，要明确物理问题和MATLAB语言之间的对应关系。很多学生在应用MATLAB语言表达物理问题的时候不够准确，往往会导致结果不准，甚至是错误的结论。因此，将一个抽象的物理问题具体用MATLAB语言描述的时候就必须抓住问题的本质，前后推敲仔细验证。第二，处理物理问题过程中要考虑到MATLAB的局限性。通常在物理学中能够测量的物理量都是实数，然而应用MATLAB进行数学计算的时候会出现复数的情况，这就需要在物理问题的描述过程中加一些限制条件。另一方面用MATLAB表示物理问题的时候是用点（或数），我们不可能取尽所有的点，那么这就存在一个精确性的问题。如果有一些特殊的点我们没有取到，就会遗漏一些重要的物理性质，因此在处理问题的时候要充分考虑MATLAB的局限性。第三，不能完全依赖MTLAB来解决物理问题。应用MATLAB的目的是辅助大学物理的学习，加深对物理问题的理解，如果过分依赖MATLAB处理问题，反而会局限学生的思维，限制学生分析问题的能力。

用MATLAB辅助学习，将烦琐的计算工作交由计算机来完成，并把抽象的问题具体化，可以很好地帮助学生解决在学习中遇到的困难，从而克服学生的恐惧心理，提高学习兴趣。本文用质点运动、电磁学和机械波等知识点为例，讨论了用MATLAB辅助学习大学物理的方法，主要探讨如何用MATLAB克服大学物理学习中的数学知识欠缺所产生的困难，以及用图形的方法将物理问题具体化的过程。同时，考虑到软件的局限性，我们也针对性地提出了应用过程中应注意的问题，这对学生的学习是非常有帮助的。为工科学生的大学物理学习提供了新的思路，丰富了大学物理的教学方法，对大学物理的混合教学具有一定的指导意义。