激光超声结合CNN的铸件缺陷检测方法

魏博文,高炜欣,刘梦溪

(1.西安石油大学电子工程学院,陕西 西安 710065；2.西安石油大学 陕西省油气井测控技术重点实验室,陕西 西安 710065)

1 引 言

金属铸件在工程使用过程中,常因高强度的负荷使得铸件损伤,并且铸件所处的恶劣环境也会使得铸件表面发生无法挽回的损伤,严重的损伤甚至导致铸件无法使用。这些损伤在工业环境中是常见的问题,例如管道在使用过程中受到腐蚀而腐蚀开裂[1]。裂纹的存在不仅使铸件失效,严重的还会引发安全问题,侵害社会的安全和经济,因此需要对这些问题进行可靠性检测。

无损检测技术(Nondestructive testing technology,NDT)可以探测铸件在制造与使用过程中的缺陷问题,从而为社会带来可观的安全效益和经济效益[2]。NDT是以保障铸件完好无损为前提,应用光、电、磁、声等多种物理现象进行多种缺陷检测的综合性技术。如今非接触式NDT方法有很多,如:静电耦合超声无损检测、空气耦合超声无损检测[3]、电磁超声无损检测、激光超声无损检测[4],4种NDT对比如表1所示。

表1 无损检测技术对比

通过对比发现激光超声无损检测技术无论是在缺陷检测方面、适用范围还是效率上都很出色。目前已有研究人员应用该技术取得了较好的缺陷识别成果,如:赵景超[5]等将样品被测前后的全息干涉条纹激光超声图像进行数值再现,再利用MATLAB软件对图像进行叠加干涉从而判断出是否存在缺陷；王余敬[6]等利用分离谱技术将样品表面不同裂纹下的回拨信号进行特征提取,再使用径向基函数神经网络识别技术来对裂纹进行识别；曾伟等提出利用Wingner-Vile算法分类处理透射波传播图像,实现对样本缺陷位置、大小和形状的检测；熊继涛[7]等使用激光超声换能器对样本激励出Lamb波,再对接收的反射信号进行延时叠加,实现对缺陷的定位；金小波[8]等将激光超声技术结合编程和软件TeeChart图形显示空间达到对接收信号的可视化,以此达到缺陷检测目的。可见,激光超声无损检测技术对铸件进行无损检测方面是可行的。本文在激光超声检测技术的基础上,提出使用结合卷积神经网络对采集的图像进行快速高效的缺陷识别。

2 激光超声检测技术

激光超声无损检测技术以不损害被检测对象的使用性能及微观结构为前提,使用脉冲激光在被测构件中产生超声应力脉冲。这一应力脉冲能够在同一时间内激发出波形不同的超声波信号,超声信号会传播被测构件的各项信息,再通过检测超声信号的反射、散射和衰减情况,进行缺陷特征描述。本文采用基于热弹机制的激光超声可视化检测仪如图1进行检测。

图1 激光超声可视化检测仪

激光超声可视化检测仪主要分为激光发射控制器、超声波探头和激光超声检测设备控制三部分。激光发射控制器对被测铸件产生激励,通过超声波探头接收信号,激光超声检测设备再对信号进行波形采集、可视化。检测原理如图2所示。

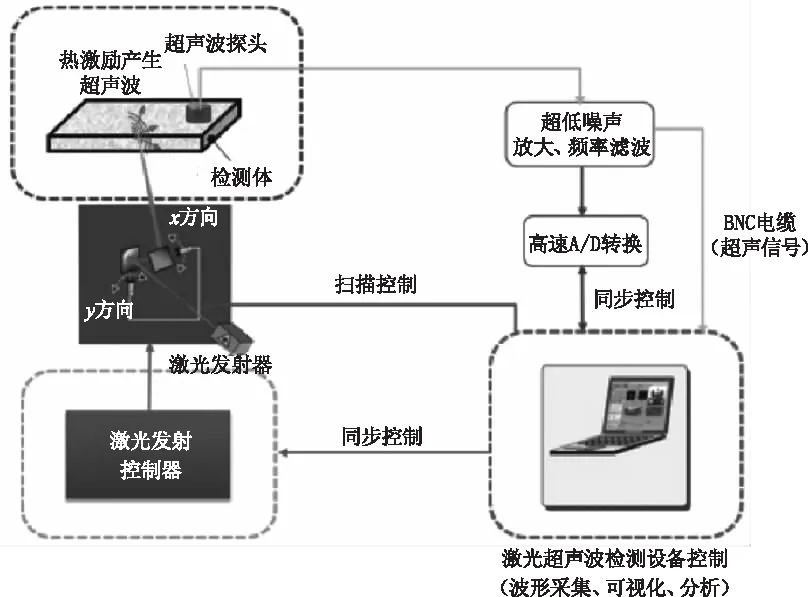
图2 激光超声原理图

激光超声可视化检测仪波长1064 nm,最大功率650 μJ,最小脉宽7 ns。实验中通过设定激励扫描范围、延迟、采样率、激励电压、数据长度和检测速度等来达到图像获取的目的。所有参数设定完毕后激光超声发射器将按照预先设定的扫描范围进行自上而下、自左至右(Y轴→X轴)的检测,设备通过探头接收信号并对该信号进行A/D转换,最终经过处理,获得最大振幅图。

3 最大振幅图采集与处理

激光超声可视化检测仪对铸件进行扫描时,缺陷处质点和无缺陷处质点会出现骤变的波动,这种骤变必然会导致信号振幅的变化,如此经过一系列处理便可获得最大振幅图。实验中对缺陷铸件进行图像采集,如图3所示为部分缺陷铸件样本图像,途中所示缺陷铸件规格为200 mm×100 mm×5 mm,其中方孔缺陷大小为5 mm×5 mm；圆孔缺陷直径为5 mm。本次实验共采集图像400张,其中无缺陷图像100张,缺陷图像300张,图4为部分最大振幅图像图像。

图3 铸件图像

图4 部分样本图像

考虑到实验只需对最大振幅图像进行是否存在缺陷的判断,为了简化实验,提高检测效率,完善CNN架构,在最大振幅图像识别之前先进行图像预处理。预处理即将三通道最大震幅图像通过灰度化转换成为单通道的灰度图像,再将灰度化的图像统一分辨率,统一成为100×100的格式。灰度化采用均值灰度化这一方式,如公式(1)所示:

f(i,j)=(R(i,j)+G(i,j)+B(i,j))/3

(1)

其中,i,j代表图像同一通道下的位置；R、G和B代表三个通道即红色、绿色和蓝色,通过计算将三个通道的像素值进行平均后再输出为一个灰度化的图像。如图5所示。

图5 灰度化样本图像

通过对图5进行分析可以发现由于图像噪声干扰较大,一般的图像处理手段难以确定最大振幅图是否存在缺陷,因此本文提出用卷积神经网络(CNN)对图像进行识别。

4 卷积神经网络及其架构

卷积神经网络[9](Convolutional Neural Network,CNN)通过卷积核(filter)将图像进行加权求和再加偏置的方式进行输出,每一次计算都可视为将输入图像依据filter大小分为一个个小的图像再进行计算输出为输出图像的一个个像素点。CNN的神经元通过响应周围单元,能够快速、高效的完成图像处理工作[10-11]。CNN不仅可以更改感受野的大小,而且它的池化层(下采样结构)可以在不影响特征识别的前提下极大的减少参数量,以此提高识别速度。相较一般的图像处理技术[12],CNN独特的图像处理方式不仅为图像处理技术提供了新的思路,更为图像处理技术带来了突飞猛进的发展。

4.1 卷积层

卷积是CNN中的一种提取输入图像特征的方法,是一种使用一个正方形卷积核遍历输入图像,将重合部分进行加权求和再加偏置[13]的方法。将计算的像素值作为输出图像的像素值,以此类推将一张图片遍历完成即可完成一次输出。如公式(2)及图6所示。

图6 卷积层计算

(2)

式中,Nout为输出图像长宽;Nin为输入图像长宽;p为padding大小;k为filter大小;s为stride大小。

由于CNN作为一个实践远超理论的研究,目前CNN卷积层设置层数大多是基于经验或者通过实验验证得到,通过阅读文献发现Cao Xudong[14]关于卷积层设置层数的结论,这里做一引用,文章中提出CNN满足2个约束条件并使用公式(3)可使卷积层层数最大化在不浪费算力时间的基础上取得较好的识别精度。

(3)

式中,z为输入图像长宽；m为卷积层层数；k为filter大小；t为固定值1/6。应用公式(3)通过计算得到m即卷积层设置层数为3,并设置2层卷积层作为对照。

4.2 卷积核

Filter是提取输入图像特征的关键,filter的结构为W×D×C×N,分别对应长宽高数量,属于人为设置,通常长宽相等,C是图像通道数channel,N是filter个数。为了提高识别效率,前文已经讲述将样本图像进行灰度化预处理,所以输入图像的通道数为1。由于filter大小只有大于1时才具有提升感受野的作用,所以通常filter不取1；由于偶数的filter会造成特征偏移从而影响识别效果,所以通常filter均为单数；通过对图5分析发现,最大振幅图中缺陷处像素点会发生梯度变化,于是此处可以引入边缘检测法[15]来对图像进行识别。边缘检测法分为3种梯度变化,即水平、垂直和倾斜三种,其公式分别为:

水平梯度:

(4)

垂直梯度:

(5)

倾斜梯度:

(6)

通过引入梯度变化设置3个filter,分别检测输入图像中的3种梯度变化。综上实际filter设置见表3。

4.3 池化层

池化层[16-17]作为降采样的一种方式,常用方法有最大池化、最小池化和均值池化3种方式。因为3种方式中最大池化能够保留输入图像信息的最大值,在提取特征时可以保留更多细节,所以实验选择最大池化方式。最大池化方式如图7所示。实验中将卷积层与池化层设置为一一对应的关系,即选择3层池化层,且设置2层池化层与之对照。池化层计算方式同公式(2),此处不做赘述。

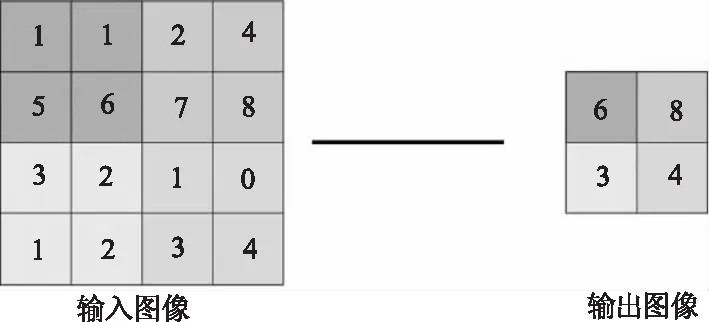
图7 最大池化

4.4 激活函数

激活函数[18]的作用时给CNN计算加入非线性因素,如果在CNN中不适用激活函数将导致每一层的计算都有关联从而使最后一层的输出和第一层的输入具有线性关系。由于缺陷检测仅用计算机对图像做出是否存在缺陷的判断,而Sigmoid函数在这种二分类问题上使用的最多,同时求导的特殊性,便于反向传播过程的计算,故使用Sigmoid函数作为激活函数。公式(7)为Sigmoid函数,公式(8)为其求导,Sigmoid图像如图8所示。

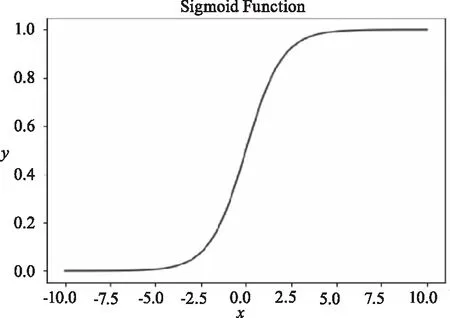
图8 激活函数Sigmoid

(7)

f′(x)=f(x)*(1-f(x))

(8)

4.5 前向与反向传播

前向传播即CNN的正向传播,将输入层的值通过卷积计算传送给下一层,直至输出层。反向传播即通过将正向传播的值与期望值做对比将误差方向传输给filter,不断地更新filter的权重,直至输出与期望值的误差达到预期目的。表2列举符号及释义。

表2 符 号

4.5.1 损失函数

文章中使用最直观的损失函数[19]:均方差损失函数[20](Mean Square Error,MSE),如式(9)所示计算a的第l层损失函数。

(9)

4.5.2 前向传播

CNN前向计算如图6所示,即对输入层进行加权求和,其公式如下：

a=w×x+b

(10)

对公式(10)进行非线性化即得到激活函数Sigmoid如下:

z=f(a)

(11)

3.5.3 反向传播

反向传播的核心是计算w和b的梯度变化,为简化计算,设置中间量δl即对第l层的z求偏导,其公式如(12)所示。

(12)

由于CNN前向计算中卷积层和池化层的计算并不相同,所以在反向传输过程中他们的反向传播计算也不相同。

已知池化层的δl推导上一层的δl-1如公式(13),其中unsample如公式(14),其中Nout为输出,Nin为输入,s为步长,f为卷积核大小,p为填充。

δl-1=unsample(δl)⊙f′(zl-1)

(13)

Nout=s(Nin-1)+k-2p

(14)

已知卷积层的δl,推导上一层的δl-1如公式(15)所示,其中rot180的意思是卷积核被反转了180°。

δl-1=δl×rot180(wl)⊙f′(zl-1)

(15)

至此可以计算卷积层的w和b,由于池化层并没有w和b,故不需计算,如公式(16)和(17):

(16)

(17)

式中,由于δl是高维张量,而b只是一个向量,所以需要将δl的各个子矩阵的项分别求和,得到一个误差向量,即是b的梯度。

4.6 卷积神经网络架构

综上所述设计实验所用CNN架构,其中数据如表3所示,架构图示如图9所示。

表3 CNN数据

图9 CNN架构

5 实验与分析

为了得到更为详尽的实验数据,并且对比出符合实验要求的结果。实验中对相同的样本设置不同的参数来进行对比,共进行4个大组进行对照。对照组(1)为卷积层层数设置为2,卷积核长宽设置为3；对照组(2)为卷积层层数设置为3,卷积核长宽设置为3；对照组(3)为卷积层层数设置为2,卷积核长宽设置为5；对照组(4)卷积层层数设置为3,卷积核长宽设置为5。其中每一组中又将样本分为四组以保障实验数据的真实性。表4为16组实验识别率。图10为16组识别率散点图。

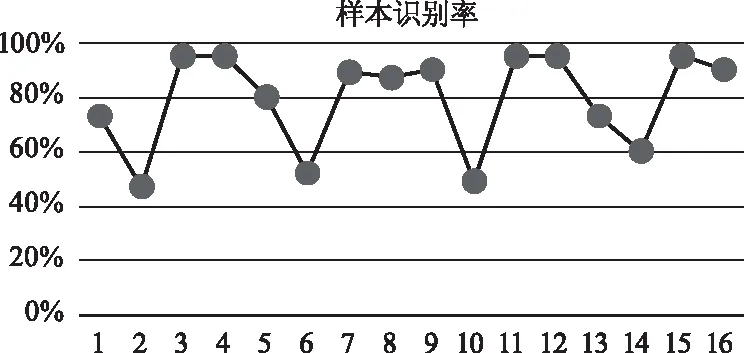
图10 样本识别率散点图

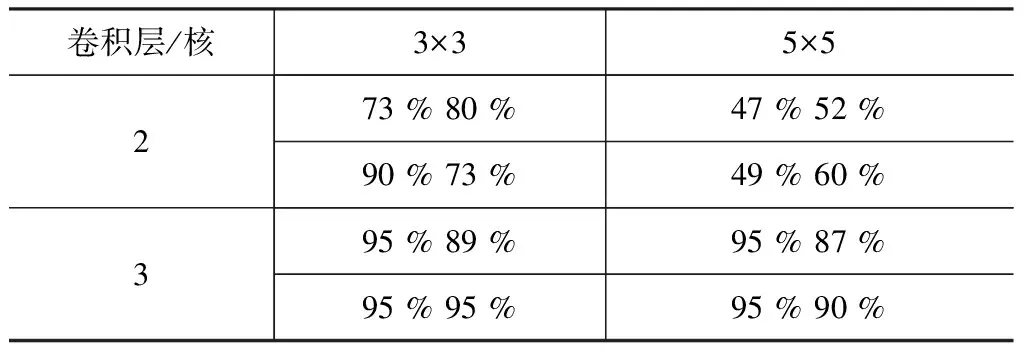
表4 样本识别率

通过对实验结果进行整理,对比不同组数据中因为卷积层数不同、卷积核大小不同以及参数量不同对识别率产生的影响,表5为4大组平均识别率、表6为卷积层相同卷积核大小不同的平均识别率、表7为卷积层不同卷积核大小相同的平均识别率。

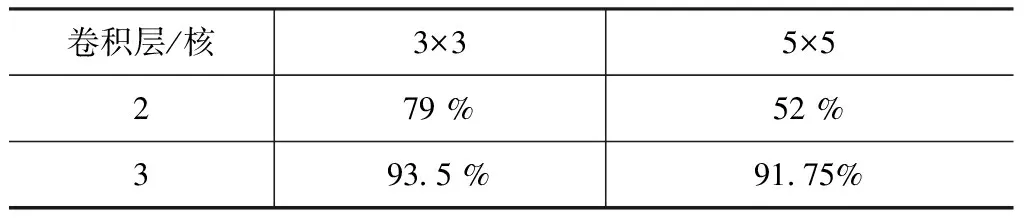
表5 平均识别率

表6 不同卷积核识别率

表7 不同卷积层识别率

通过表中汇总数据分析得到:表2显示识别率最高的是卷积层数3卷积核3×3达预期要求。表3显示卷积层数3相较于卷积层数2的识别率提升27.125%；表4显示卷积核3×3相较于卷积核5×5的识别率提升14.375%。综上,通过实验印证本文预先设计的卷积层数3卷积核大小3×3能够较好的完成铸件缺陷检测要求,本次实验中的平均识别率可达93.5%,达到实验预期。

最后识别错误的图像与识别正确的图像进行了对比,图11为部分识别错误图像,图12识别正确的图像。

通过对比图11和图12发现识别错误图像与识别正确图像存在一定相似性。考虑到边缘检测的应用,识别错误的原因既有可能是因为这一原因所导致,图13为无缺陷图像中可能存在的边缘检测识别,图中箭头表示该方向上可能存在的边缘检测判断。

图11 部分识别错误图像

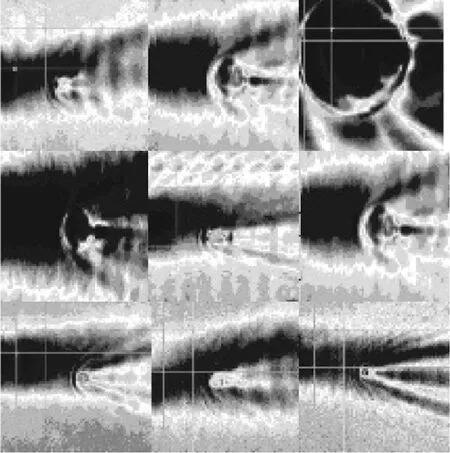
图12 识别正确图像

图13 识别错误图像与边缘检测

实验中发现最大振幅图成像效果的参差对于识别效果产生了很大的影响。在样本采集过程中发现激光强度设置为70 %、采样率为10 Ms/s、检测速度500 Hz所取得的图像效果较好。通过实验验证,本次实验较好的完成了铸件缺陷的识别工作。

6 结束语

本文提出将激光超声检测技术与卷积神经网络技术结合,帮助提高铸件缺陷检测效率。经过预先设计和实际验证,设计出一个符合本次实验识别精度要求,检测经过激光超声可视化检测仪输出的最大振幅图像的卷积神经网络架构,经过多组对照实验验证发现,预先设计的卷积神经网络架构能够较好地完成实验任务。未来可以通过对比更多的卷积神经网络架构,得到一个更好的检测最大振幅图像的卷积神经网络架构。