面向SOI波导-单模光纤耦合的硅微透镜设计

李雄飞,韩明玺,疏 静,王 雷,桂 桑,岳玉涛,顾文华

(1.南京理工大学电子工程与光电技术学院,江苏 南京 210000;2.无锡市德科立光电子技术股份有限公司,江苏 无锡 214000;3.江苏集萃深度感知技术研究所有限公司,江苏 无锡 214000)

1 引 言

实现硅波导与光纤的高效耦合同时满足较高集成度是硅基光子技术用于高速光纤通信必须解决的关键问题之一。绝缘体上硅(SOI)波导的Si-SiO2-Si结构对光有很好的约束力,且相比其他材料的光波导如SiN、Ge∶SiO2等,可以做到更高的集成度,并于主流半导体硅工艺高度兼容,前景广阔。因此,本文着重研究了基于硅微透镜对SOI波导和单模光纤进行高集成度耦合的问题。

除了常见的楔形、光栅、光纤端面拉锥等耦合结构[1-6],使用透镜结构对波导和光纤耦合也一直是被研究的重点之一。但是常规尺寸的耦合透镜多为从传统光学衍生发展的分立式的二氧化硅透镜,使用于半导体发光器件/波导至单模光纤的远场耦合[7-12],其工艺成熟,有较大的对准容限,但体积过大,成本较高,不利于集成和封装。因此,在硅基平台直接集成的微型耦合结构无疑是具有研究价值和应用前景的,这就要求在微小结构尺寸和较近距离尽量减少二者之间的模场尺寸失配(SMF-Core∶9.86 μm,SOI∶<3.5 μm)和折射率失配(SMF-Core∶1.468,Si∶3.45)带来的耦合损耗。

相比于纳米线波导,微米级的波导意味着可以承受更高光功率和更好的工艺容错性,最关键的是能够容易与单模光纤的光场尺寸匹配。最近,关于厚硅3 μm的SOI工艺已经展现出实用阶段的集成潜力,如芬兰国家科技研究院VTT[13]的3 μm波导工艺,已经做到0.1 dB/cm 的低传输损耗,端面耦合损耗可低至0.5 dB。另外,英国Rockley[14]的3 μm波导工艺降低条形波导(Strip-waveguide)的传输损耗至0.3 dB/cm,最高可承受10 W的光功率；而且,Rockley通过Euler-band结构将其弯曲直径降至1.3 μm,解决了大截面波导的弯曲损耗问题。

因此,本文根据高斯光束传播理论设计了一种基于3 μm SOI波导工艺边缘集成的硅微透镜耦合结构(如图1所示),并使用光束传播(Beam Propagation Method,BPM)算法仿真分析其在1550 nm波长下的近场耦合效果,仿真结果表明可实现近场90 %耦合效率,该设计可为实际应用提供理论依据和仿真指导。

用硅基微透镜作为耦合结构的特点是:①微透镜尺寸小,可在硅基端直接刻蚀,更易于采用成熟硅工艺进行规模化制备和集成。②硅材料折射率为3.45,因此相比于常规材料透镜(如SiO2),会将耦合焦距和腰斑位置距离缩短,便于集成；如本文设计的三种透镜都是将光纤和波导的耦合距离控制在近场范围内并达到80 %的耦合效率,避免了远场耦合的对准不确定性和能量的发散损耗。③微透镜对准容差相比于常规尺寸透镜耦合要小,尚存在优化空间,这也是高集成度所带来的必然结果。

2 BPM法计算耦合效率原理

波导与光纤的耦合主要有四部分损耗:传输损耗、Fresnel反射损耗、对准偏差损耗、模场失配损耗。当波导结构、耦合位置确定时,可基于BPM算法分析仿真三维波导到光纤的耦合过程,计算耦合效果。

2.1 基础模场理论

基于Maxwell方程对均匀平面波导(如图2)进行导模条件分析,可结合边界条件得到TE、TM模式本征方程和标量亥姆霍兹方程:

(1)

(2)

2.2 BPM算法

基于BPM算法可对传输路径每个截面的标量场从二维平面波导(x,z)标量场到三维(x,y,z)进行拓展求解。标量场表示式是按亥姆霍兹方程(2)通过网格离散推导的波动方程(3),截面网格如图3所示。

图3 三维波导截面网格

(3)

φ(x,y,z)=u(x,y,z)exp(-ikz)

(4)

(5)

通过给定输入场u(x,y,z=0),迭代求解出z>0方向的场的演化过程。对于波动方程的矢量推导[15-17]即表示场的横向分量(Ex和Ey),相应的缓慢变化场(ux和uy)满足如下耦合方程组:

(6)

其中,Ψij是复微分算子:

(7)

方程(7)为全向量的BPM方程,对于TE、TM模式,算子Ψxx和Ψyy考虑了界面上不同边界条件引起的偏振依赖性,并且描述了不同的传播常数、场形状、弯曲损耗等对运算结果的影响。算子Ψxx和Ψyy解释了几何效应引起的极化耦合和模式混合。另外,Ψxx=Ψyy=0为半向量的近似条件,此时横向场分量是解耦的,这样在简化计算的同时保留了其偏振特性。

根据重叠积分算法可计算出对准模式下空间某点的模式匹配效率:

(8)

除了模式匹配损耗,还需要存在Fresnel反射损耗,根据Fresnel公式计算该耦合结构的端面反射损耗:

(9)

Rloss=-10 lg(R)

(10)

经Zemax软件对透过率计算,使用硅透镜于空气中和单模光纤耦合,1550 nm波长下将有～53.2%的Fresnel反射损耗,该损耗可以通过在耦合端面镀抗反射(AR)膜来改善,如在SOI端面镀SiNxOy∶H膜层,单模光纤端面镀氟化镁(MgF2)膜层,以实现反射损耗的抑制。目前,这些AR膜在光通信窗口的实际透过效果可达99 %以上[18-19]。因此,下一节的仿真结果已对这部分反射损耗予以补偿计算,不再讨论未镀膜情况。

3 结构设计

3.1 波导、光纤建模

按照SOI脊型波导的单模工作条件(γ>0.5)进行建模[13,14,20],如图4所示,设置脊型波导内脊宽度、厚度:w=h=3 μm,外脊厚度:d=0.6h=1.8 μm；SiO2层、硅基底厚度均大于1.5 μm。单模光纤设置纤芯:折射率n1=1.468 μm、芯径r1=8.6 μm；包层:折射率n2=1.456、直径r2=125 μm。背景折射率设为n=1。

在Rsoft软件中用1550 nm波长光源计算光纤和波导的基模(TE:Ex、Hy),设计结构(图4)中3 μm脊形波导和芯径8.6 μm的标准基模Ex分布如图5所示。

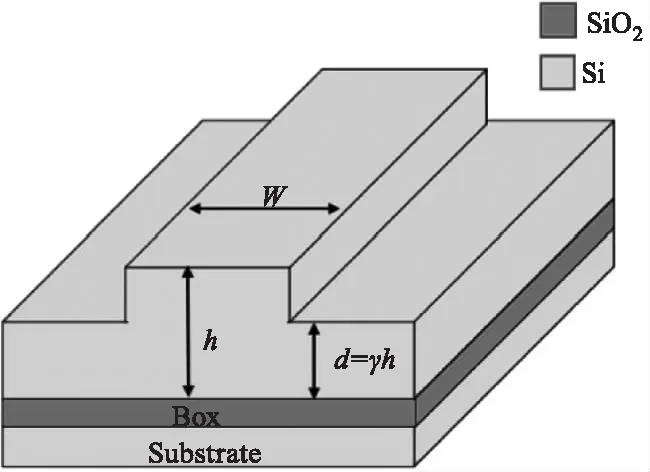
图4 脊型SOI波导[15]

(a)脊形波导

实际在三维矩形波导中,并不能得到标准的TEM模式,而是在传输方向有微小分量的准TEM模式。由于光纤为圆柱波导,波导的光场受横向限制,故光纤的标准基模为高斯圆斑,模场能量近似高斯分布,不旋转对称,因此硅波导和单模光纤中两个模场的初始形状、尺寸匹配度并不高,需要在中间加入耦合匹配结构。

3.2 微透镜设计

使用微透镜完成波导模场和光纤模场的有效匹配,边缘耦合是一种可行的集成方式。首先,需要注意的是射线光学中的数值孔径NA可计算多模光纤的最大入射角度和导模条件,但对于单模光纤的发散角估算是不准确的,单模光纤芯径一般不超过10 μm,纤芯中仅存在近似0度入射的最低阶导模。所以,单模光纤耦合应该着重考虑光纤的模场直径(MFD)和该过程中高斯光束的传输特性[21-22],不应将出射光源简单地当作点光源处理。高斯光束经透镜耦合前后的波束变化如图6所示,可以根据式(11)、(12)设计透镜参数:

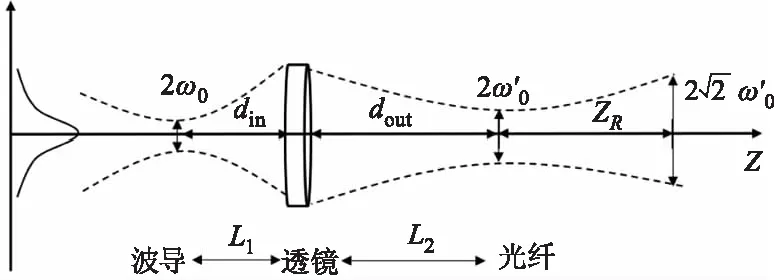
图6 高斯光束经透镜耦合

(11)

(12)

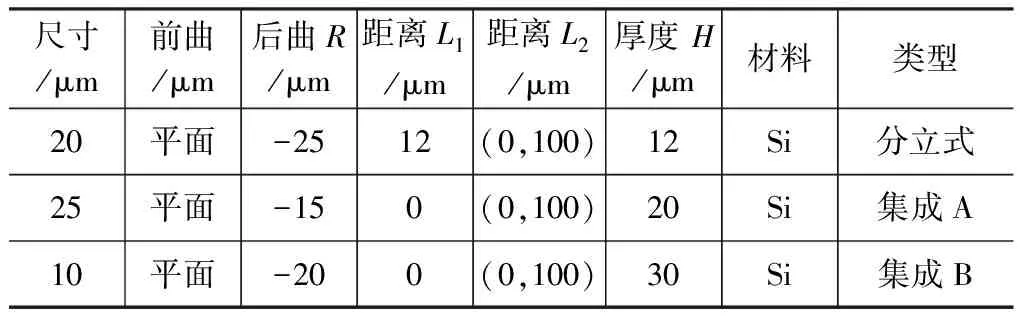
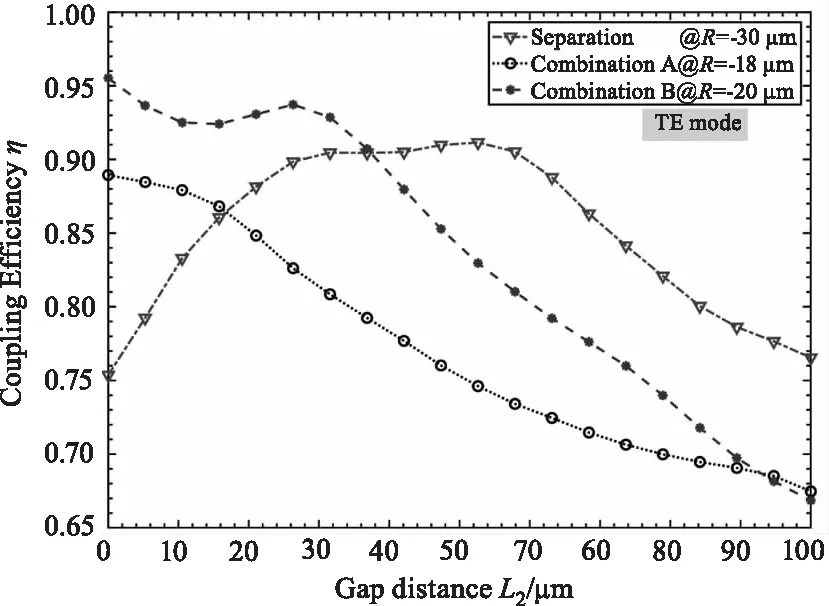
假设波导出射束腰直径约为3～4.5 μm的标准高斯光束,基于高斯光束传播理论,若要与模场直径9～10 μm光纤耦合,则透镜焦距需要近似满足13.6 μm

本文研究了与硅波导分立式与硅波导集成式的透镜结构设计,表1为初始设计参数,图7为时域有限差分法(FDTD)仿真的在空间尺寸3 μm且波长为1550 nm的高斯光源下三种微透镜前后腰斑尺寸和位置关系。其中分立式透镜前曲面距波导端面距离为L1,两种集成式透镜(A、B)直接与波导端面贴合即L1=0。

图7 三种微透镜前后腰斑-空间位置关系及耦合示意图

表1 透镜典型设计参数

4 仿真分析

采用BPM方法仿真计算了在激励基模模式下沿Z方向的脊波导和单模光纤纤芯中的光场分布,仿真区域值设置为(30,30,z):硅波导正Z向出射波长1550 nm光束经过微透镜改变光束传播途径以限制光束入纤角度,并进行一定程度的模斑转换,经空间传播后入射纤芯,如图7(d)所示。由于光在空间中传输了一段距离,因此入射纤芯的模场并不是稳定的场,包含了导模和辐射模,只有满足纤芯导模条件的成分会被耦合入光纤继续传播,并被监视器计算耦合光场(入纤长度为200 μm)的重叠积分。

波导出射并不是高斯圆斑,虽然在不同位置的光场切片可以观察到微透镜也能进行一定程度上的模斑转换,但是腰斑位置和光束的发散特性与理论设计仍会有一定偏差。通过对表1设计的三种透镜通过仿真扫描后曲率R、端面-光纤距离L2与耦合效率η的关系可得到在1550 nm波长单模1 dB耦合损耗的最佳曲率参数,见表2。

表2 1550 nm单模条件最佳耦合参数

图8选取了三种参数对透镜与光纤端面距离L2对耦合效率的影响进行了计算扫描,可见分立式结构的1 dB耦合距离是较长的,此结构分立距离为12 μm。两种集成透镜(A、B)更适宜近场耦合,经仿真分析,这三种透镜在100 μm范围内可以实现68 %以上的耦合效率,且TE/TM耦合结果显示三种结构都存在有一定偏振模式差异,譬如R=-30 μm分立式透镜偏振差异约2.4 %,R=-18 μm集成式A透镜的偏振差异约5 %,R=-20 μm集成式B透镜存在1.8 %的偏振差异。另外,在耦合中也会存在端面错位造成的损耗,通过在在空间设置光纤和波导错位参数,可研究三种透镜在端面平行对准情况下的错位损耗容限。

(a)TE模

对光纤基于不同透镜与波导对准耦合时(与Z向平行)可能出现的横向偏移量δx、纵向偏移量δy对耦合效率(TE模式)的影响分析结果如图9所示。因为波导出射模斑在y轴方向的模式尺寸较小,三种透镜在(x,y)截面y方向的偏移更加敏感,所设计的三种透镜在整体结构横纵偏移量在<1.5 μm时可有80%以上的耦合效率。

5 总 结

本文通过初步设计仿真证明,基于高斯光束传播理论设计的波导边缘集成的硅基微透镜用于硅波导到单模光纤的光学耦合是可行的,在保证对准精度的情况下在近场可有～90%的耦合效率。这种耦合结构可作为硅波导集成器件与单模光纤进行近距离光学互连的一种普遍手段,如阵列波导光栅(AWG)芯片出射波导与光纤的耦合,为硅光子器件的耦合与集成化研究提供了新的研究方法。