基于参数化风场的浙江沿海风暴潮数值模拟

罗佳敏，姜云鹏，庞亮，冯钰栋

( 1. 中国海洋大学 工程学院，山东 青岛 266100；2. 交通运输部天津水运工程科学研究所，天津 300456；3. 山东电力工程咨询院有限公司，山东 济南 250013)

1 引言

台风是我国东南沿海常见的气象灾害，影响范围广、发生频次高、变异性强、破坏力大，由台风引发的风暴潮灾害是破坏沿海地区人民生命财产最主要的方式之一[1]。浙江省是台风影响频率最高、受灾最为严重的省份之一，2000-2016年共有46场台风对浙江省造成影响[2]。在气候变化的背景下，风暴潮发生的频率不断增加，精细化且能真实反映风暴增水变化的风暴潮数值模拟研究显得尤为重要。

台风是风暴增水最直接的驱动因素。风场的可靠性直接影响到风暴潮数值模拟的准确度。风暴潮数值模拟中多采用基于简化的物理模型和数值模型的参数化台风风场模式。1980年，Holland[3]根据澳大利亚低纬度海域台风数据，提出了Holland模型。在最大风速半径(Rmax)的基础上，引入Holland参数，即径向气压分布系数(B)，用来描述台风径向剖面结构的变化，使模型具有更普遍的适用性[4-6]。研究发现，Rmax和B对台风风场结构及风速的影响较大[7-9]。Powell等[10]基于美国东南沿海地区的飞机探测数据对B进行了拟合研究，给出了B关于Rmax和纬度 ϕ的拟合关系式；Vickery和Wadhera[11]将B与Rmax关联，提出了B与Rmax和中心气压差(ΔP)的拟合公式；在澳大利亚海域，Love和Murphy[12]、Hubbert等[13]、Harper和Holland[14]分别给出了B与ΔP的拟合公式；Jakobsen和Madsen[15]根据孟加拉湾海域台风资料，提出了B与ΔP、1 min最大风速的拟合关系；在西北太平洋海域，江志辉等[8]结合《热带气旋年鉴》数据，利用地球物理流体动力学实验室（Laboratory of Geophysical Fluid Dynamics,LAGFD）的部分计算方法，得到ΔP关于Rmax的拟合曲线公式；李瑞龙[16]结合李小莉等[7]关于Rmax的计算方法，认为Rmax服从对数正态分布，同时拟合得到我国沿海台风多发地区的Rmax计算公式；Fang等[17]利用中国气象局（China Meteorological Administration, CMA） 最佳路径数据集，根据1949-2016年的历史台风数据，给出B关于ΔP和纬度ϕ的拟合关系式，构建了适用于西北太平洋海域的参数化风场模型。

近年来，诸多学者针对我国沿海海域进行了台风风场研究。唐建等[18]将CCMP（Cross Calibrated Multi-Platform）背景风场与多种经验风场模型结合，模拟了1105号台风，发现Holland模式的模拟结果与实测数据较接近。程雨佳等[19]将联合概率法与Holland参数风场模型结合，推算得到台风影响下南海海域的波高重现期。潘冬冬等[6]发现在南海海域，将欧洲中期天气预报中心（ECWMF）第五代再分析资料（ERA-5）背景风场与选用Hubbert等[13]提出的B计算方法构建的Holland风场模型相叠加得到的台风风场，能较好地重现台风“山竹”的风速过程。方根深等[20]基于典型台风过程建立风场模型并针对我国南部沿海进行了模型适用性研究，通过对比不同的B、Rmax计算公式，认为在西北太平洋海域，采用卢安平等[21]提出的B、Rmax组合方案进行“黑格比”台风风场的模拟具有较高的精度。

针对影响浙江沿海的风暴潮灾害，诸多学者采用不同的数值模型开展了相关研究。孙志林等[22]运用Delft-3D模型，探究了舟山渔港风暴潮位对不同台风路径的响应规律。丁骏等[23]采用MIKE 21水动力模型，建立了浙江沿海的二维风暴潮模型，准确模拟了1323号台风风暴潮过程。陈洁等[24]利用MIKE 21模型，选用0608号台风，进行海平面上升情景下的台州市玉环市的风暴潮数值模拟，发现玉环市北侧登陆的台风风暴潮对海平面上升较敏感。何威等[25]选用Holland模型，对B、Rmax参数公式进行比选构建9711号台风模型，并使用MIKE 21模型研究了椒江河口不同形态变化对风暴潮的影响，认为河口收窄会使风暴高潮位抬升。

上述研究结果显示，不同海域获得的风场参数拟合方法差异较大，因此需综合比较不同的计算方法以获得适用于浙江海域的参数化风场模型，在此基础上能够对典型台风诱发的风暴增水进行合理的数值分析。本文以该海域常用的Holland模型为切入点，比较风场模型中最大风速半径Rmax和径向气压分布系数B的计算方法，以0216号台风“森拉克”、0414号台风“云娜”为例，分析Rmax和B不同计算方法的组合对风速发展的影响，由此得到适用于浙江海域的参数化风场模型。基于生成的输入风场，利用MIKE 21模型进行该海域的台风风暴潮数值模拟，与实测数据比较，进行天文潮位和风暴增水水位验证与分析。

2 参数化风场模型及其关键参数

Holland模型[3]的径向气压分布公式为

式中，Pr为距离台风中心r处的气压；Pc为台风中心气压；ΔP=Pa-Pc，为台风中心气压差，Pa为台风外围气压， 取1 010 hPa；Rmax为台风风场最大风速半径；B为径向气压分布系数。

梯度风场模型的计算公式为

式中，Vg(r)为距离台风中心r处的梯度风速；ρA为空气密度，取1.2 kg/m3；f=2Ωsinϕ，为科氏力系数，其中，ϕ为台风中心纬度。

式（2）Rmax中和B的表达式大多是基于实测或数值模拟的拟合结果[20]，应用较为广泛的计算表达式见表1和表2。

由表1和表2可以看出，台风风场模型中各个参数间相互影响，特别是Rmax和B与台风中心气压差ΔP、中心纬度ϕ、中心移动速度Vf等之间可能都存在一定的关系，并且不同海域获得的风场参数统计拟合关系差异较大，需对计算方法进行综合比较来确定参数组合计算模式。

表1 径向气压分布系数B的主要计算表达式Table 1 Main calculation methods of radial pressure profile coefficient B

表2 最大风速半径Rmax的 主要计算表达式Table 2 Main calculation methods of maximal wind velocity radius Rmax

为得到适用于浙江沿海的台风风场，本文基于前人总结的参数经验公式，分别选取3个典型且适用于我国沿海海域的径向气压分布系数B、最大风速半径Rmax的计算方法，对应组合得到9种不同的参数组合方案，下文称自匹配模式。B、Rmax的计算表达式及编号见表1和表2，9种自匹配模式的组合情况见表3。

表3 自匹配模式Table 3 Self-matching patterns

3 参数化风场的验证

3.1 台风选取

基于CMA最佳路径数据集[30-31]提供的台风轨迹、中心气压及台风中心最大风速等数据，采用表3所示的自匹配模式，得到不同Rmax和B组合关系的9种参数风场模型，再现0216号台风和0414号台风在发展过程中的风速变化。为验证风场的准确性，本文选取大陈、石浦、嵊泗气象站的实测风速数据与数值模拟结果对比。图1给出了两场台风的轨迹示意图以及实测站点的位置。

3.2 风场验证

根据现有资料，对海平面10 m高度风速进行验证，图2、图3分别为0216号台风、0414号台风的风速对比结果。

从图中可以看出，9种自匹配模式模拟结果与实测风速在变化趋势上基本相似，但在不同台风中，各模式在风速极值与台风影响前期的风速模拟上差别较大。R3计算方法在极值风速的模拟上相对偏大，R1、R2方法模拟结果相近。B1、B2计算方法在台风影响前期风速和极值风速的模拟上效果较好，B3计算方法整体风速偏小，不能很好地反映风速变化特征。

为更好地评估各种计算模式的计算偏差，选用相关系数C0与极大值相对误差C1进行检验，公式如下：

式中，Fi、Oi、Fmax、Omax分 别为模拟值、实测值、模拟值最大值和实测值最大值；N为样本总容量。

采用极大值相对误差C1来评价模型在预测极值风速上的精度，采用相关系数C0来评价台风整体过程中模拟风速的综合效果。当C0=1.0时，表示两变量完全线性相关；一般情况下，若C0＞0.8，就可认为两变量相关性较好。相关系数和均方根误差结果见表4。

由表可知，综合不同台风及不同站点的相关系数和相对误差，自匹配模式B1R1在9个模式中是和实测结果符合度最好的，其次是B1R2。由此可知，选用江志辉等[8]提出的R1计算方法以及Jakobsen和Madsen[15]的B1方法进行台风风场的构造，能较准确地反映该区域台风风场特征。

图1 台风轨迹及气象站实测站点Fig. 1 Track of typhoon and location of weather observation sites

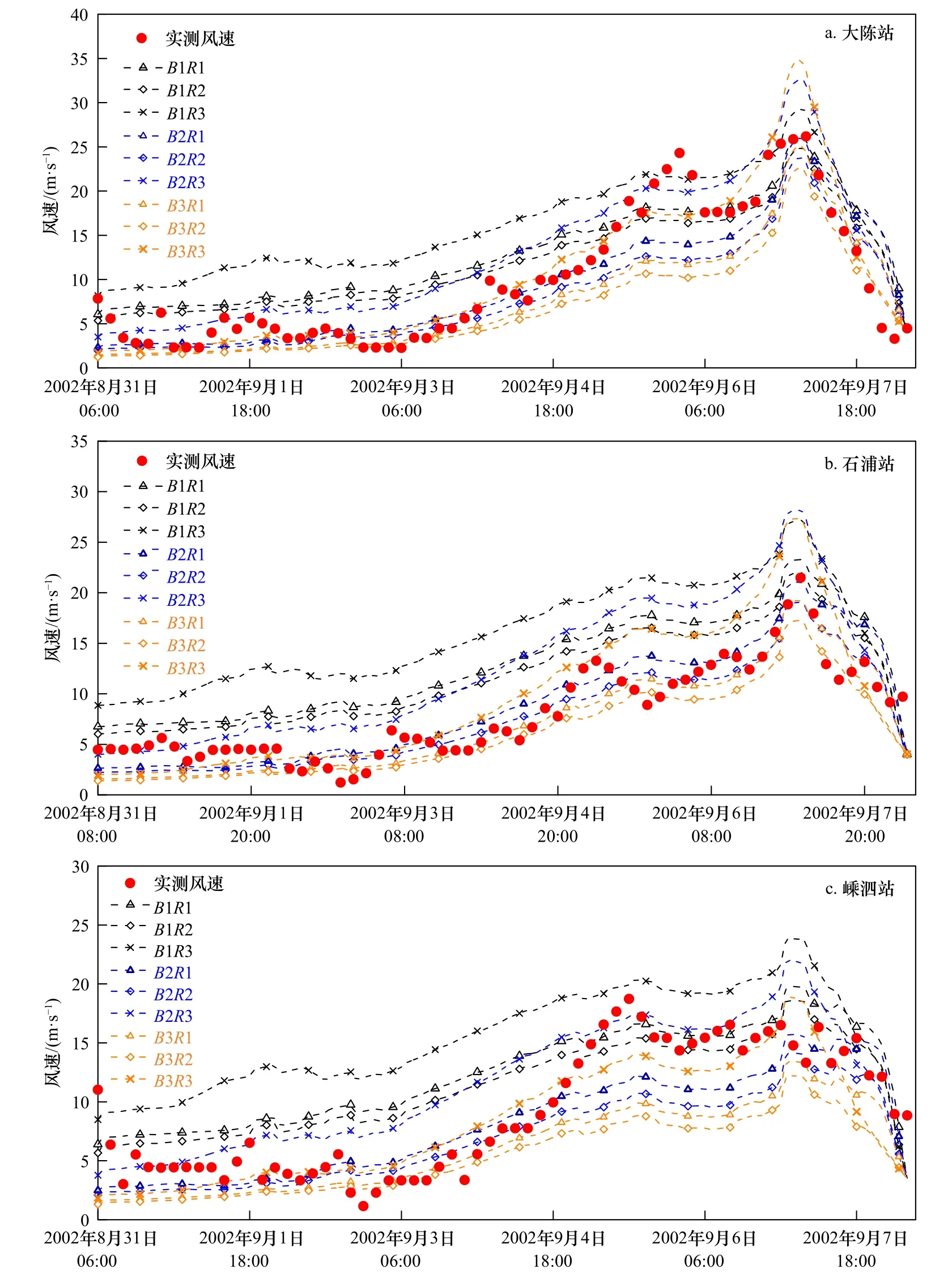
图2 0216号台风风速数值模拟结果与实测对比Fig. 2 Comparison of Typhoon 0216 wind speed between simulated and observed results

4 风暴潮数值模拟

4.1 模型设置

本文基于MIKE 21水动力模型，结合Holland 参数风场模型和全球潮汐模型TPXO 7.2，建立了天文潮-风暴潮耦合数值模型。该模型将二维水动力模块与海面风强迫力相结合，在风暴潮模拟研究中具有良好的适用性[32-33]。

模型以浙江海域为研究对象，天文潮-风暴潮耦合模型计算海域为26.1°～31.0°N，120.1°～124.35°E，如图4a所示。考虑到浙江沿海岛屿众多、岸线复杂，计算域采用不规则三角网格划分，网格从外海至近岸逐渐加密，外海网格最大分辨率为9.5 km，近岸台州沿岸网格分辨率为50～200 m，宁波、温州海域网格分辨率为100～1 000 m。整个计算域共287 503个单元、146 733个节点，网格图见图4b。模拟区域的岸线数据采用美国国家海洋和大气管理局（NOAA）的高精度岸线数据；宁波市石浦港至温州市鳌江口一带的近岸海域水深由海图数字化得到，其他海域的水深数据引用NOAA的30″×30″的ETOPO1水深数据，模型最小时间步长为 0.1 s，最大时间步长为60 s。

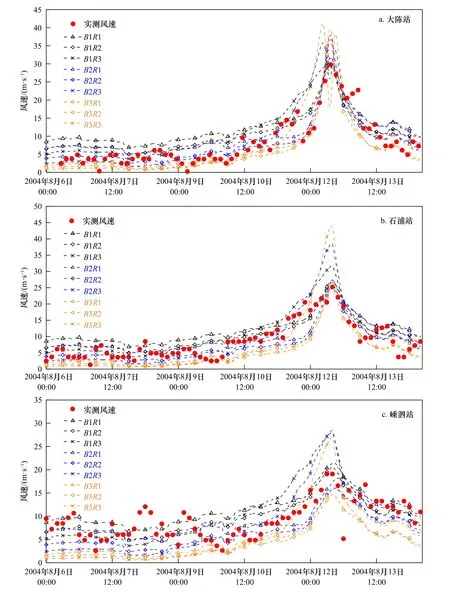
图3 0414号台风风速数值模拟结果与实测对比Fig. 3 Comparison of Typhoon 0414 wind speed between simulated and observed results

4.2 模型的验证与分析

4.2.1 台风资料

0216号 台 风 于2002年8月29日6时（UTC）生成，9月7日10时30分（UTC）在浙江苍南登陆, 登陆时中心气压为965 hPa，近中心最大风力达12 级以上。登陆时, 温台等地出现了狂风巨浪、暴雨高潮等现象，沿海最大风速超40 m/s，且台风过程正值天文大潮期，实测资料显示台风过程中整个浙江沿岸最高潮位均超警戒水位，浙中、浙南岸段受灾尤为严重[34]。0414号台风于2004年8月8日12时（UTC）生成，12日12时（UTC）在浙江温岭市石塘镇登陆，登陆时近中心风速与中心气压分别为45 m/s和950 hPa。0414号台风强度高、风力大、影响范围广，是1956-2004年间在浙江沿海登陆的最强台风。台风登陆适逢天文大潮起潮期，引起登陆点附近潮位站2.30～3.58 m的最大增水。

表4 风速计算值与实测值的误差Table 4 Error between simulated and observed results of wind speed

图4 模型水深图和网格图Fig. 4 Water depth map and grid map of modle

选取上文的参数化风场模型生成的0216号台风和0414号台风风场作为天文潮-风暴潮耦合模型的驱动风场，对两场台风影响下的天文潮潮位及风暴潮增水水位进行验证，台风路径见图5。

4.2.2 天文潮验证

潮汐和风暴潮的非线性作用在风暴潮增水模拟中尤其重要[35]。检验天文潮-风暴潮耦合模型能否较好反映沿岸的水位变化情况，首先要进行潮位验证。进行潮位验证时，模式只给予开边界潮汐水位驱动，不加入风场。本文根据国家海洋信息中心提供的2002年和2004年潮汐表中浙江省的7个潮位站的潮位预报数据进行天文潮潮位验证，验证站点位置见图5。

两场台风模型的模拟时间分别为2002年8月29日6时至9月8日6时（UTC）、2004年8月6日0时至8月14日0时（UTC），软启动时间均为72 h，软启动期间不进行潮位验证，天文潮验证结果如图6、图7所示。

图5 台风路径及验证站点Fig. 5 Track of typhoon and location of verification sites

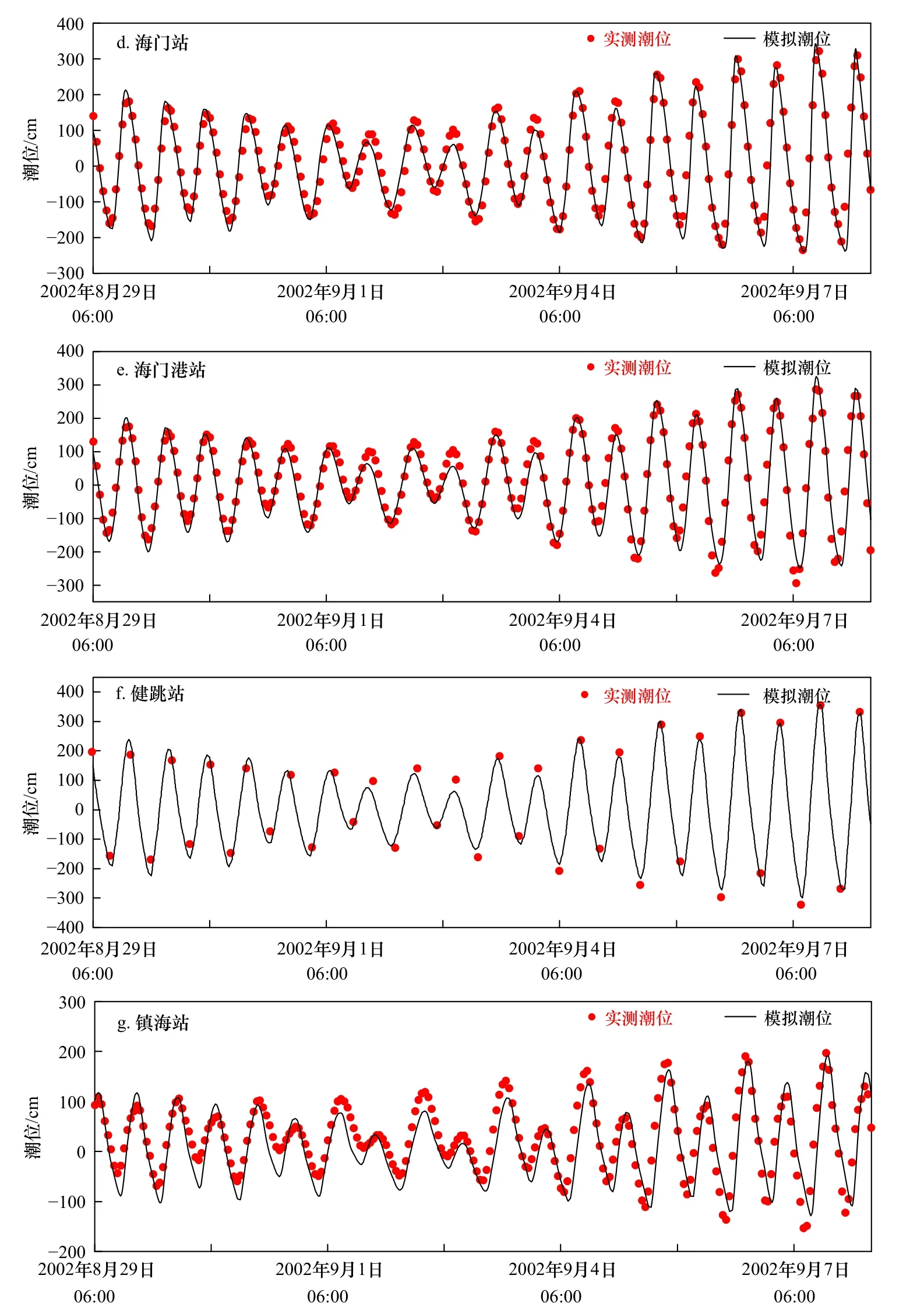
图6 0216号台风期间天文潮位数值模拟结果与潮汐表对比Fig. 6 Comparison of tide level between simulated and tide table value during Typhoon 0216

由图可知，潮位模拟值与实测值整体趋势较为一致，在各站点符合较好。

0216号台风期间，从潮时差来看，各站高低潮位出现时间与潮汐表数据的相位差在1 h左右，误差原因是健跳站、坎门站在8月29日至9月2日的高潮潮时提前约1 h；东门村站、海门港站、镇海站在9月4-8日的低潮潮时滞后约1 h。从潮位差来看，7个站点的潮位高潮绝对平均误差最大为0.16 m（镇海站），最小为0.03 m（黄大岙站）；低潮绝对平均误差最大为0.24 m（镇海站），最小为0.10 m（海门站、坎门站）。其中，坎门站模拟高潮位偏低，海门站、海门港站在高潮位模拟中的误差主要源于9月1-4日3次低高潮的潮位偏低。

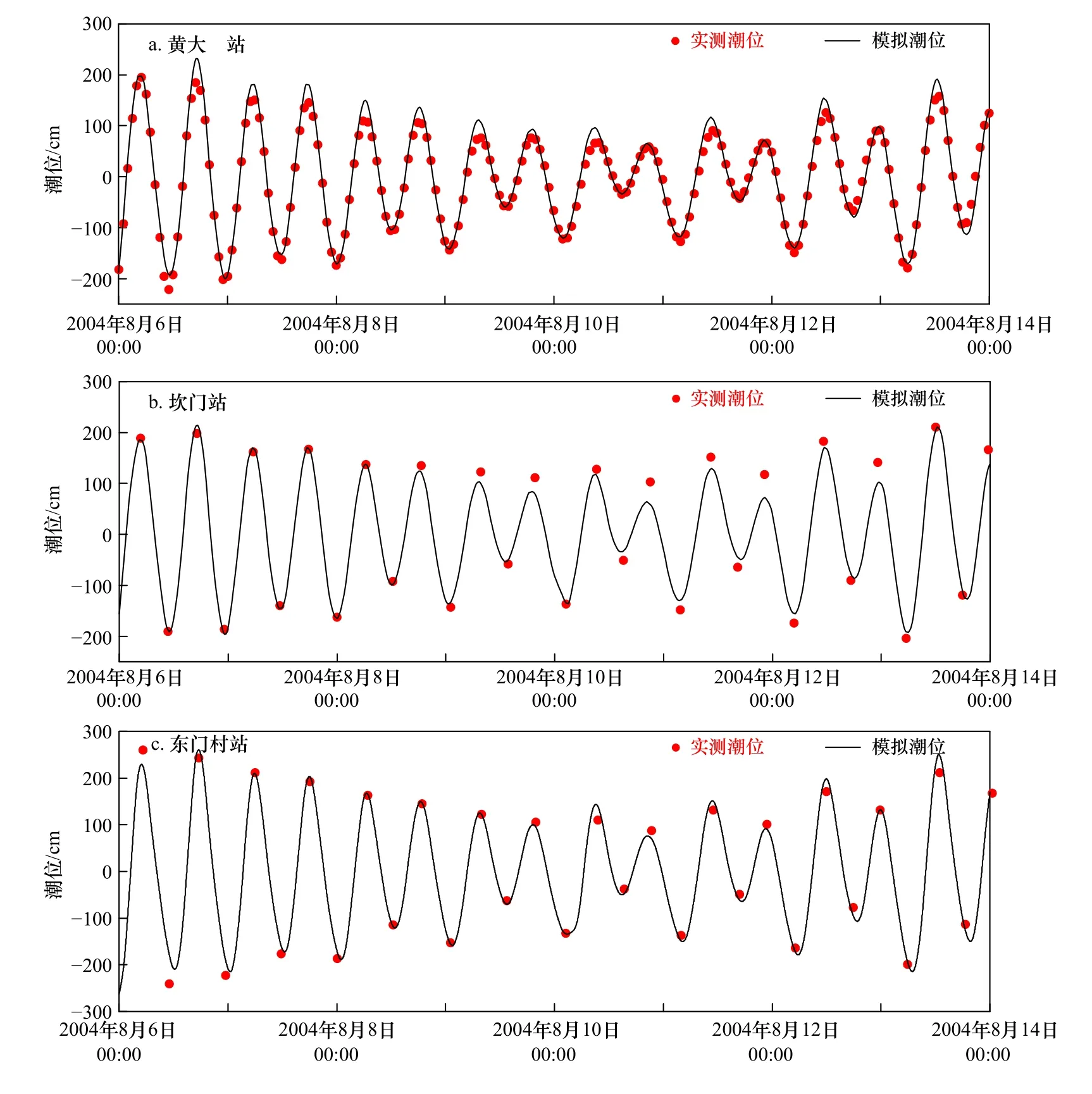
0414号台风期间，各站高低潮位的出现时间与潮汐表数据的相位差在1 h左右，误差主要是东门村站、海门港站、海门站、健跳站在8月6-8日以及12-14日的低潮潮时滞后约1 h导致。6个站点的潮位高潮绝对平均误差最大为0.23 m（海门港站），最小为0.09 m（东门村站）；黄大岙站模拟高潮位偏高，健跳站、坎门站、海门站、海门港站在8月10-13日的3次低高潮的模拟潮位偏低。低潮绝对平均误差最大为0.27 m（健跳站），最小为0.05 m（坎门站）；除健跳站在低潮位的模拟中误差较大外，其余站点低潮绝对平均误差均在0.1 m内。

可以看出，模型模拟结果与潮汐表数据较为一致，能够较好地反映研究区域的潮位变化特征。但也存在一定误差，例如个别站点在模拟后期出现低高潮位、相位滞后的问题，如健跳站、坎门站、镇海站整体相比其他站点不能很好地再现潮位的变化等。产生的主要原因如下：

（1）模型本身的误差。建立模型时，为确保计算效率，个别站点分辨率较低，导致模拟潮位误差，如健跳站、镇海站；同时，个别站点水深较浅、地形特殊，非线性效应显著，易导致潮波畸变；另外，模型中未考虑漫滩也是造成结果差异的原因之一。

（2）初始潮位及验证资料的误差。一方面，模型选取TPXO 7.2在外边界的模拟结果来确定模型开边界潮位，与实况存在一定误差；另一方面，验证资料选自潮汐表，忽略了实际水位是潮汐项和扰动项之和。

（3）模拟过程中的误差。模型以开边界潮汐水位为驱动，进行由外海向近岸的计算，模拟范围较大，会增大近岸的累积误差[36]；此外，不同天文潮位时实际海床糙率不同，难以在模型中准确反映[23]。

4.2.3 风暴潮增水验证

模拟总水位与模拟天文潮水位相减可以得到风暴潮增水水位。其中，模拟总水位是在模拟中添加潮位和风场的共同驱动得到。

0216号台风与0414号台风增水的模拟结果与实测数据的对比分别如图8、图9所示。从图中可以看出，风暴潮增水的模拟结果与实测值的过程吻合度较好，主峰契合。

图7 0414号台风期间天文潮位数值模拟结果与潮汐表对比Fig. 7 Comparison of tide level between simulated value and tide table value during Typhoon 0414

0216号台风期间，坎门站距离台风中心较近，其过程风暴潮增水较大，出现的增水是标准型增水过程；海门站、健跳站呈现波动型增水过程；镇海站呈现混合型增水过程。从风暴潮主振阶段来看，各站峰值时间差在1 h内，风暴潮增水极大值最大误差出现在海门站，为0.19 m；最小误差出现在坎门站，为0.09 m；4个站的平均误差为0.14 m。除海门站以外，其余站点误差均在0.15 m以下。从先兆波增水情况来看，4个站在趋势上与实测增水情况符合，出现先兆波的周期性增水且增水时间长；但先兆波的周期性增水水位较实测值偏低0.05～0.60 m，其中，海门站、坎门站模拟效果稍好，除个别周期的先兆波增水水位的模拟误差大于0.5 m外，其余的增水水位误差在0.05～0.30 m范围内，健跳站、镇海站模拟水位误差较大，偏低0.10～0.65 m。除模型中岸线和水深数据的可靠性因素外，误差可能和站点与台风中心的距离、网格精度有关。先兆波是由外海强风低压所引起的自由长波，由台风中心向外传开，并比台风中心超前传至岸边，站点离台风中心较远会导致摩擦损耗以及累计误差，例如离台风行进路径相对较远的健跳站、镇海站，先兆波增水模拟误差较其他站点偏大；同时，先兆波发生时期，站点附近风力较小，风暴潮与天文潮的耦合作用偏弱，也会导致模拟增水过程波动不明显。另一方面，网格精度的问题也可能会导致难以准确刻画先兆波的增水情况。

图8 0216号台风期间增水水位数值模拟结果与实测对比Fig. 8 Comparison of storm tide between simulated and observed results during Typhoon 0216

0414号台风期间，各站点距离台风中心较近，过程增水水位较大，呈现标准型增水。从风暴潮主振阶段来看，各站峰值时间差均在1 h内，风暴潮极值增水最大误差出现在海门港站，为0.22 m；最小误差在海门站, 为0.15 m；3个站的平均误差为0.18 m。除海门站以外，其余站点误差均在0.20 m以下。综上，可以认为模型能够较好地模拟台风过程中的风暴潮增水变化情况。

图9 0414号台风期间增水水位数值模拟结果与实测对比图Fig. 9 Comparison of storm tide between simulated and observed results during Typhoon 0414

5 结论

本文基于Holland参数化风场模型，研究了台风风场模型中关键参数最大风速半径Rmax和径向气压分布系数B对风速的影响，将3种典型的Rmax、B参数计算公式进行对应组合得到9种不同的参数化方案，对其在两场台风下的各站点风速模拟值进行了验证分析；采用选定的Holland参数风场模型构成的0216号台风和0414号台风风场作为输入风场，利用MIKE 21数值模型进行浙江海域风暴潮数值模拟，并对实测站点的天文潮位及风暴潮增水水位进行了验证分析，得出如下结果。

（1） 采用参数计算方法比选的方式确定Holland参数化风场模型，能使风场模拟更为准确。针对参数化风场模型中不确定性较强的最大风速半径Rmax和径向气压分布系数B，不同的参数风场公式获得的风速模拟结果表现出明显的差异。选用大西洋海域Graham[29]的最大风速半径Rmax方法所得的风场模型在极值风速的模拟上偏大，Powell等[10]的径向气压分布系数B方法在台风影响前期的模拟风速偏小。采用江志辉等[8]、Fang等[27]提出的Rmax计算方法及Jakobsen和Madsen[15]、Fang等[17]的B计算公式组合得到的参数风模型能较准确地重现研究区域台风过程的风速变化情况。

（2）浙江沿海地区，采用江志辉等[8]的Rmax和Jakobsen及Madsen[15]的B方法确定的参数化风场模型可较准确地模拟台风过程中整体与极值风速的变化特征。

（3）基于本文提出的风场参数选取方法构建台风场，输入MIKE 21风暴潮数值模型，在风暴潮增水的模拟精度上已经达到要求。从风暴潮主振阶段来看，各站增水最大时间误差在1 h内，增水最大值误差在0.25 m以内，平均误差在0.15 m左右。从先兆波增水情况看，0216号台风模拟过程中，各站风暴潮增水趋势与实测情况相符，但在增水水位上偏低0.05～0.60 m不等，这可能是由于地形、岸线数据及网格精度等问题导致。未来可采用更高分辨率或是选用台风发生期间的岸线水深数据，提高风暴潮数值模型的准确性。